Анализ оснований теории относительности, метод определения реального темпа хода часов в движущихся системах отсчёта и вычисление привилегированной системы

Введение

Физиками 19-го века (Ампер, Фарадей) была обнаружена зависимость состояния физических тел от скорости их движения v. Сразу возник вопрос, относительно какой системы отсчёта (СО) измерять эту скорость v. Странным образом получалось, что отсчёт от лабораторной системы давал удовлетворительные результаты, несмотря на то, что уже было известно о движении Земли, как минимум, вокруг Солнца. Трудами Лоренца, Пуанкаре и других физиков было показано, что такая ситуация может происходить вследствие изменения состояния движущихся тел в соответствии с преобразованиями, названными впоследствии преобразованиями Лоренца.

Эйнштейн предположил, что в качестве исходной можно брать любую инерционную систему отсчёта (ИСО). Это вызывало возражения многих учёных, в том числе – Пуанкаре. Более подробно эти возражения изложены в первой главе настоящей статьи. До эры космических полётов они имели скорее теоретическое, чем практическое значение. Специальная теория относительности Эйнштейна не рассматривала реальный ход часов, и вопрос, в какой ИСО часы идут быстрее, в СТО неразрешим.

В настоящей статье показано, что методом обмена серией электромагнитных импульсов прецизионной периодичности вполне достоверно определяется реальный темп хода часов движущихся объектов. При этом неминуемо выяснится система отсчёта с самым быстрым ходом часов. Она и будет привилегированной для данного региона.

Показано, что для многих процессов (но не для всех!) система отсчёта Земли является привилегированной.

Полученные результаты имеют существенное значение для расчёта траекторий, телеметрии, дистанционного и автоматического управления космическими аппаратами.

1. Неизотропность движущихся систем отсчёта

В качестве исходной системы отсчёта Эйнштейн [1, с. 8] принимал изотропную и однородную инерционную систему отсчёта ИСО1, т. е., одинаковую во всех направлениях и не зависящую от выбора начала координат. В этой ИСО1 он располагал ось x так, чтобы она совпадала по направлению со скоростью v, но изотропность и однородность самой системы отсчёта сомнению не подвергалась. Нет никакой причины считать исходную систему отсчёта анизотропной и неоднородной, т. к. внешние поля предполагаются отсутствующими.

Вследствие однородности и изотропности исходной системы отсчёта величина отклонения параметров движущихся физических тел от параметров неподвижного состояния не может зависеть ни от выбора начала координат, ни от направления скорости v, а ТОЛЬКО от её абсолютной величины.

Например, ход часов выразится формулой:

, (1)

где t, t₀, соответственно – показания движущихся и неподвижных часов.

Согласно исследованиям учёных конца 19 – начала 20-го века f(|v|) – однозначная строго монотонная функция.

Конкретно, в преобразованиях СТО Эйнштейна [1, с. 19]:

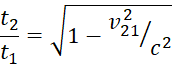, (2)

Где c – скорость света,

t₁, t₂, соответственно – показания часов в исходной и движущейся ИСО,

v₂₁ – скорость ИСО2 относительно исходной ИСО1.

Предположим, что мы имеем 3 тела, движущихся в одном направлении, но с разными по модулю скоростями v₁, v₂, v₃ относительно ИСО0, причём:

v₁ = v₂ – ∆v,

v₃ = v₂ + ∆v,

v₂ ≠ 0.

Очевидно, что, согласно формуле (1), изменение процессов вследствие движения тела 1 будет меньше, чем тела 2, а тела 3 – больше, чем тела 2.

Перейдём теперь в ИСО2. Естественно, переход в другую ИСО не может сам по себе изменить ход часов. Все часы, двигавшиеся относительно ИСО0 со скоростями v₁, v₂, v₃, будут идти в прежнем темпе. Нам же интересно, как это будет выглядеть из ИСО2. Глядя из ИСО2, мы будем видеть разные скорости процессов в теле 1 и теле 3 при одной и той же величине относительной скорости |∆v|. Т. е., одинаковые с точки зрения ИСО2 скорости ∆v, но направленные в разные стороны, будут оказывать разные воздействия на физические тела. Повторим, что v₂ ≠ 0, т. е., ИСО2 – движущаяся.

Таким образом, произвольная ИСО, движущаяся относительно ИСО0, будет неизотропной.

Любая неизотропная СО не может быть эквивалентной изотропной ИСО0, т. е., провозглашённый А. Эйнштейном принцип равноправия всех ИСО (принцип относительности) несовместим с зависимостью состояния тел от скорости их движения. Изотропной в отсутствии силовых полей может быть лишь одна единственная – абсолютная система отсчёта (АСО).

Формула (2) получена Эйнштейном для конкретных часов (в общем случае – для конкретных тел, процессы в которых служат показателем времени), неподвижных в ИСО', из формулы, впервые полученной Лоренцем:

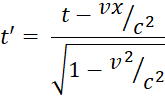, (3)

Где t и t' соответственно – показания часов в неподвижной и движущейся ИСО.

x – координата часов в исходной ИСО.

Лоренц искусственно ввёл так называемое «местное время» t' для приведения вида уравнений микроскопических электродинамических систем в движущейся ИСО' к тому же виду, что и в неподвижной [2, с. 809].

Эйнштейн получил свои решения не в результате рассмотрения фактического поведения физической системы, а в результате искусственного приведения хода часов и размера объектов к требованию одинаковости скорости света в различных ИСО.

Рассмотрим последовательность действий Эйнштейна [1, с. 17].

Он берёт две идентичные ИСО и начинает одну из них (ИСО΄) двигать. Читатель, полностью ознакомившейся с его статьёй представляет, что ИСО΄ (как и исходная ИСО) оснащена множеством часов, которые, в процессе придания ей скорости v, меняют темп своего хода в соответствии с формулой (2). Подразумевается, что стрелки всех часов в обеих ИСО в момент времени t = 0 находились на нулевой отметке. Когда стрелки на часах исходной ИСО достигают отметки t, снимаются показания всех часов ИСО΄. Естественно, что, поскольку все точки ИСО΄ предполагаются физически ничем не выделенными (пространство однородно) и действия с часами ИСО΄ абсолютно одинаковыми, то все показания t΄ для разных точек должны совпадать! Собственно, формула (2) как раз свидетельствует об этом.

Откуда же взялась неидентичность хода часов в ИСО΄?

Как уже было отмечено выше, он искусственно привёл ход часов и размеры объектов к требованию одинаковости скорости света в различных ИСО.

Кстати, из структуры формулы (3) видно, что ИСО´ неоднородна и неизотропна: параметры её преобразований зависят от выбора начала координат и направления оси x. Она не может быть эквивалентной исходной изотропной ИСО.

Под конец жизни Пуанкаре осознал, что два и более преобразования СТО некоммутационны, несоединимы, что как раз является следствием неизотропности движущихся ИСО. Он подверг острой критике теорию относительности, о чём свидетельствовал сам Эйнштейн.

После встречи Пуанкаре и Эйнштейна на Сольвеевском конгрессе в Брюсселе в 1911 г. Эйнштейн пишет своему другу Цангеру: «Пуанкаре отвергал всё начисто и показал, при всей своей тонкости мысли, слабое понимание ситуации».

Здесь, под коммутационностью имеется в виду «соединяемость», т. е., последовательное применение преобразований времени в СТО [1, с. 6-35]:

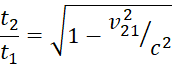, (4)

и

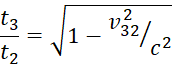, (5)

неэквивалентно преобразованию

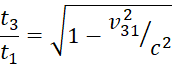, (6)

В равенствах:

t₁, t₂, t₃, соответственно – показания часов в своих инерциальных системах отсчёта ИСО1, ИСО2 и ИСО3 при условии, что в начале отсчёта времени все показания часов в этих ИСО были равны нулю,

v_ki – скорости ИСОk относительно ИСОi.

В неэквивалентности результата преобразований (4) и (5) преобразованию (6) можно убедиться непосредственной подстановкой. Особенно ярко это видно, если скорость v₃₂ противоположна по направлению скорости v₂₁: v₃₂ = –v₂₁. Таким образом, преобразования теории относительности нетранзитивны и нерефлексивны.

Возражение некоторых теоретиков, что v₃₁ в этом случае необходимо вычислять как релятивистскую сумму v₂₁ и v₃₂, разрушает концепцию равноправия инерционных систем отсчёта, требует учёта предыстории этих систем, в том числе – исходной ИСО, и, фактически, приводит к необходимости существования некой корневой ИСО0, от которой и должны отсчитываться все скорости v_i0 и все ожидаемые показания часов в различных ИСОi:

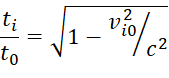, (7)

t_i, t₀, соответственно – показания движущихся и неподвижных часов.

Точно к таким же выводам – необходимости учёта предыстории и существования АСО – приводит и искусственное введение так называемых обратных преобразований Лоренца. Многие сторонники СТО не замечают, что сама исходная эйнштейновская ИСО может быть результатом предыдущего преобразования, противоположного тому, которое после осуществил Эйнштейн. Неопределённость исходной ИСО в СТО неминуемо приводит к неопределённости, какое именно преобразование: прямое или обратное – необходимо применять для получения адекватного физического результата.

Пуанкаре придерживался в своих работах представления об абсолютном пространстве, независимо от того, доступно оно для наблюдения или нет. И хотя он понимал, что наблюдатели в различных системах отсчёта найдут одно и то же значение для скорости света при принятой синхронизации часов, это соглашение, эта инвариантность были для Пуанкаре всего лишь искусством измерения, см. [3, с. 341-358].

По этим причинам он не стал претендовать на авторство СТО, хотя вся математика 4-мерного пространства, в сущности, принадлежит ему.

Из приведённого анализа ясно, что отсчёт хода часов от произвольной системы отсчёта может привести к ошибкам (произволу). В настоящей работе приводится способ более точного определения параметров движущихся систем методом обмена серией электромагнитных импульсов прецезионной периодичности.

2. Уравнения Игла-Тангерлини

Одновременно с изменением темпа процессов в движущемся теле, как установил Д. Д. Томпсон в 1881 году, меняется коэффициент в уравнении 2-го закона Ньютона, называемый массой.

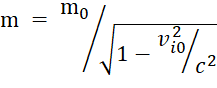_, (8)

Где m₀ – масса тела, покоящегося в АСО.

Формула (4) подтверждена в огромном количестве экспериментов ядерной физики и работой ускорителей. Заметим, что при расчёте томпсоновской массы, как и в уравнениях Максвелла, имелась в виду скорость от эфира – некой привилегированной системы отсчёта, а в отсутствие силовых полей – от АСО.

Только потом СТО начала трактовать (8) как релятивистскую массу. Нетрудно заметить, что отсчёт скорости v от произвольной ИСО лишает формулу (8) всякого смысла, как физического, так и математического. Недаром в последнее время сторонники ТО избегают понятия «релятивистская масса».

В отличие от (8) формула (7) не имеют подтверждения при больших v/c. При очень больших скоростях коренным образом меняется физическое состояние тела, а не просто темп хода часов. Об этом свидетельствуют уравнения Лиенара-Вихерта и концепции квантовой хромо- и электродинамики, см. [4, с. 17; 5, с. 18, 112].

По этой причине формула (7) соответствует реальности при не очень больших скоростях.

В этом случае:

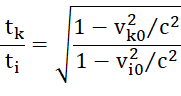, (9)

Мы получили уравнения Игла-Тангерлини, см., например, [6; 7, с. 111-134; 8].

Прямая проверка результатов СТО не могла быть проведена в начале XX века, она и сейчас требует специфических условий. В частности, если верно предположение о движении солнечной системы в направлении созвездия Льва, то часы космических аппаратов, движущихся от Земли в этом направлении, будут идти медленнее, а часы на аппаратах, движущихся в противоположную сторону (к созвездию Водолея) – быстрее, чем часы на Земле.

Это имеет практическое значение: расчёт траектории космических тел, движущихся в сторону Водолея, будет отличаться от расчёта траектории в сторону созвездия Льва.

3. Сравнение темпа хода часов в различных СО методом обмена серией электромагнитных импульсов прецезионной периодичности. Вычисление привилегированной системы отсчёта

В специальной теории относительности, в сущности, отрицается сама постановка вопроса о том, какие из движущихся часов идут быстрее, а какие медленнее. Мы не будем приводить здесь многочисленные дебаты по этому вопросу, отметив, что все разъяснения сторонников ТО так или иначе грешат нарушением логики.

Инженеры GPS элементарно решили этот вопрос.

Не вдаваясь в конкретные детали работы навигационных систем, рассмотрим простейшую схему решения поставленной задачи для открытого космоса. Установим на космических объектах генераторы и приёмники электромагнитных импульсов. Предположим, что импульсы посылаются по местным часам через t секунд, а в принимающих СО интервалы составляют соответственно (t + Δt₂) и (t + Δt₁) сек. Средняя величина Δt = (Δt₁ + Δt₂)/2 характеризует «разбегание» СО1 и СО2

, (10)

Разность δt = Δt₂ – Δt₁ определяет темп хода местных часов. Для существующих скоростей космических объектов в пределах Солнечной системы δt << t и:

, (11).

Накопление статистики по величинам t₂/t₁ и соответствующая экстраполяция позволят определить систему отсчёта с самым быстрым ходом времени. Она и будет привилегированной для данного региона, а в случае отсутствия силовых поле – абсолютной системой отсчёта.

В процессе этих измерений можно определить закономерности распространения электромагнитных волн (ЭМВ), по которым в настоящее время имеется ряд вопросов. В частности, скорость ЭМВ по-настоящему может быть изотропна только относительно АСО. Описанный метод позволит определить также влияние гравитации и движения на часы различной конструкции, реальные частоты электромагнитного излучения на Земле и на спутниках и реальное изменение частоты ЭМВ в гравитационном поле.

4. О синхронизации часов в гравитационном поле

Способ синхронизации часов методом обмена серией стандартизованных по местным часам электромагнитных импульсов по формулам (10) – (11) для часов, находящихся в гравитационном поле, требует дополнительного обоснования.

При приближении скорости тела к скорости света ускорение уменьшается по закону:

, (12)

Где F_x – действующая сила,

α = (1 – v²/c²)^1/2,

m = m₀ /α – томпсоновская масса.

В случае гравитационного поля F_r/m = g и

, (13),

Т. е. при приближении скорости частицы к скорости света её ускорение стремится к нулю.

Фотон движется быстрее любой другой частицы, и, согласно (13), он осуществляет предельный случай v = c, a = 0, следовательно, скорость света в гравитационном поле сохраняет величину c. Исходя из этого, двухсторонняя скорость тем более не меняет своего значения в гравитационном поле, что позволяет применить формулы (10) ÷ (11) в малых полях тяготения и исследовать таким способом темп хода часов для различных высот, что имеет значение в системе ГЛОНАСС.

В работе [9] Фландерн принимает возможность сравнения хода часов на спутниках и Земле как само собой разумеющийся факт.

5. Почему система отсчёта Земли является привилегированной для колебательных процессов и вращательных движений?

Соотношения (9) Игла-Тангерлини имеют многочисленные следствия. Остановимся на весьма характерном случае обращения или колебания тела 2 относительно центрального тела 1, например, Земли.

При небольших v₁₀/c на основании (9) мы можем с точностью до записать:

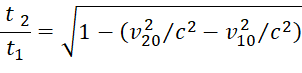, (14)

Представим вектор v₂₀ в виде суммы:

v₂₀ = v₁₀ + v₂₁,

Где v₂₁ – вектор скорости 2-й частицы относительно 1-й.

Разлагая движение v₂₁ по оси v₁₀ и перпендикулярным ей осям, возводя в квадрат (v₁₀ + v₂₁) и интегрируя по полному циклу v₂₁, получаем:

, (15)

Где v_21orb – модуль орбитальной (или колебательной) скорости движения частицы 2 относительно тела, движущегося со скоростью v₁₀.

При интегрировании по полному циклу колебаний (или вращения), член, содержащий произведение v₁₀v₂₁ обращается в нуль ввиду того, что вектор v₂₁ попеременно и симметрично принимает положительные и отрицательные значения, а v₁₀ в данной задаче полагается постоянной.

Итого получаем:

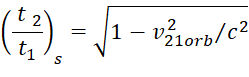, (16)

Где значок s означает усреднение по полным циклам.

Формула (16) прямо-таки мистически совпадает по форме с формулой (4)!

Но по идеологии она в корне отличается от формулы Эйнштейна. Системы отсчёта СО1 и СО2 в (16) неравноправны!

Если мы рассмотрим все случаи применения формул замедления времени: опыты Хафеле-Китинга, работа GPS и ускорителей – то окажется, что все они подчиняются уравнению (16), а вовсе не СТО, т. е., СТО на практике никогда не применялась! – см. [9; 10, с. 285-288].

Конкретные измерения на спутниках ГЛОНАСС и GPS доказывают, что замедление темпа из-за движения испытывают именно часы спутников, а не часы на Земле. Кстати, взаимное движение спутников относительно друг друга никак не отражается на показаниях часов вопреки СТО и прекрасно описывается формулой (16).

Любопытно, что, если СО с одним из близнецов совершит движение по замкнутому пути, то, согласно (16), промежуток времени для этого облёта Δt_2s = Δt₁*(1 – v_21orb ² /c ²)^1/2 меньше Δt₁ – времени, которое прожил оставшийся на Земле близнец, т.е. эффект близнецов, являющийся для СТО парадоксом, получает в теории Игла элегантное объяснение, не требующее отсылки в ОТО.

Выводы

1. Двухсторонний обмен электромагнитными импульсами прецизионной периодичности позволяет определить, вопреки утверждениям некоторых теоретиков, реальный темп хода часов в движущихся относительно друг друга системах отсчёта. Эти измерения имеют большое значение в вопросах телеметрии, дистанционного и автоматического управления космическими аппаратами.
2. Преобразование Лоренца (3) зависимости времени от координат не отражает естественного поведения объектов при изменении скорости, а является лишь условием искусственного приведения уравнений в подвижной ИСО к тому же виду, что и в неподвижной.
3. Предположение Эйнштейна о равноправии инерционных систем несовместимо с фактом зависимости состояния физических тел от скорости движения.
4. Поскольку уравнения общей теории относительности (ОТО) получены как переход из одной мгновенной ИСО в другую, затем в третью и т. д. [11, с. 313] при ложном предположении о равноправии этих ИСО (т. е., именно то, что Пуанкаре считал категорически недопустимым), то эти уравнения нельзя признать адекватными действительному поведению материи. Дополнительным замечанием к составлению этих дифференциальных уравнений является неучет квантовых, диссипативных и других взаимодействий, превосходящих гравитацию в малых областях на ~40 порядков.
5. Эти выводы не являются совершенно новыми. При внимательном анализе работы GPS, ГЛОНАСС и других навигационных систем легко выяснить, что принцип равноправия ИСО в них не действует, о чём имеются сообщения в иностранной печати [9].
6. Наиболее заметные отклонения формул Игла от теории относительности имеют место в дальней космической навигации, поэтому при этой навигации необходимо, как минимум, кроме теоретических расчётов, иметь независимые системы контроля.
7. В дальних космических сверхмассивных объектах при больших отклонениях от ньютоновских решений общая теория относительности приводит к многочисленным парадоксам, которые казались неприемлемыми даже самим теоретикам ТО. Хотя эти парадоксы не влияют непосредственно на повседневную жизнь, они заложены в мировоззренческие теории и насаждают ложную идеологию.
8. Ложная идеология, о которой говорится в предыдущем пункте, безальтернативно насаждается в образовательных учреждениях, не позволяя развиваться творческим способностям учащихся и тормозя научно-технический прогресс.
9. Другие следствия являются предметом дальнейших теоретических разработок и экспериментальных проверок.