Развитие электродинамики и физики на основе теории мироздания. Часть 1

Вначале отметим, что формальный подход в математике и физике приводит к ошибочным результатам, и, в частности, в электродинамике. Приведем известное математическое соответствие обычных уравнений Максвелла волновым уравнениям. При этом учтем, что для вектора F верно известное математическое соотношение [1, с. 20]:

, (1)

Чисто математически ноль справа соответствует нулю слева. Так как замкнутое изменение слева должно дать и замкнутое изменение справа, то есть чуда появления из ничего быть не может, и при этом преобразования связанные с операцией воздействия ротора (rot) не приводят к переходу в противоположность, так как слева и справа от знака равенства сохраняется исходная напряженность поля. Но вот дальше при замене F на реальное магнитное поле Н получаются чудеса, связанные с обычными уравнениями Максвелла и правилом возможности обнуления в математике, так как принимается что div =0, и тогда уравнение (1) можно представить так:

, (2)

Данная математическая запись не имеет зависимости напряженности магнитного поля от времени, при этом есть вторая производная по магнитному полю. Однако если учесть известный закон Вио-Савара-Лпласа, с применением операции (rot) на основе стационарного магнитного поля при учете уравнений [2, с. 88-89], то в электродинамике получим:

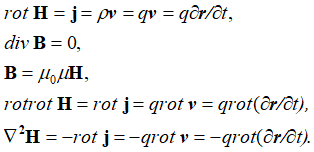, (3)

Чисто математически это означает движение заряда по замкнутому кругу, и мы имеем зависимость от времени из-за наличия производной по времени. Соответственно движение заряда по замкнутому контуру дает изменение кинетической энергии в направлении движения по прямой линии. Это означает, что должно происходить излучение кинетической энергии в направлении движения и поглощение кинетической энергии в перпендикулярном направлении. Иными словами, должно быть наличие силы торможения с потерей кинетической энергии, и силы получения кинетической энергии при замкнутом движении. В противном случае будет потеря кинетической энергии частицей. То есть, ни о каком стационарном магнитном поле речи быть не может, если есть динамика через излучение и поглощение. Излучение и поглощение кинетической энергии осуществляется через волновые процессы электромагнитного поля (ничего иного реально не наблюдается). Однако, при рассмотрении перехода от обычных уравнений Максвелла к волновым уравнениям электромагнитного поля, в среде распространения, куда происходит излучение и откуда получается дополнительная кинетическая энергия, никаких зарядов нет! Тогда мы приходим к парадоксу . Отсюда дальнейшие преобразования для получения уравнения волны, исходя из движения заряда, теряют смысл, так как нет зарядов для движения с некоторой скоростью v. Кроме того, даже если предположить что такие заряды с массой покоя в среде существуют, то для взаимодействия с излучением и поглощением для формирования движения волн со скоростью света, они также должны двигаться со скоростью света (иначе нельзя сформировать электромагнитную волну), а при массе покоя зарядов это невозможно. При этом надо заметить, что формирование замкнутого магнитного поля от движущегося заряда со скоростью v в некоторой точке пространства происходит через среду распространения. А это означает, что уже в среде распространения должны быть условия для формирования магнитного поля на расстоянии от движущегося заряда. То, что, среда распространения является необходимым элементом (отдельным объектом), говорит и накопление энергии в магнитной катушке, в противном случае этого процесса в принципе быть не могло. Следовательно, отсюда следует вывод, что должен быть вариант, когда происходит не движение зарядов, а преобразование напряженности магнитного поля в иной вид со скоростью света. Собственно, это заметили и физики, поэтому в электродинамике на практике этот иной вид получил название сторонних токов и зарядов [3, ч. 119; 4, с. 300]. Отсюда уравнения Максвелла приобрели вид [5, с. 116]:

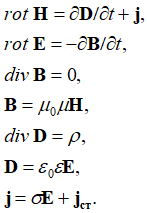, (4)

Понятно, что проводимость – (), в среде распространения равна нулю, как и нет самих движущихся зарядов со скоростью v, и остается только сторонний ток . В соответствии с этими уравнениями была сделана подстановка вместо значения эквивалентной величины по первому уравнению Максвелла (4) что фактически означает взаимодействие электрических и магнитных полей. В результате, с учетом того, что в среде распространения электрическая и магнитная проницаемость являются константами, имеем [5, с. 116]:

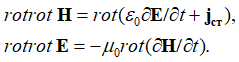, (5)

Кроме того, так как, электрическая и магнитная составляющие – это противоположности в силу их связи через скорость света (Н=сЕ), то такая подстановка возможна, если произошел переход в иную систему наблюдения. Это связано с перестановкой переменных длины на время за счет перестановки операций дифференцирования по времени и длине, и наоборот, что и было сделано в виде:

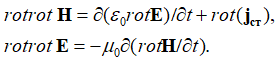, (6)

Далее используются замены в соответствии с первыми двумя уравнениями Максвелла по (4) с возвратом в исходную систему наблюдения:

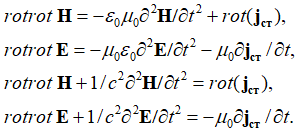, (7)

При представлении произведения роторов через уравнение (1) получают с учетом уравнений Максвелла (4) вид:

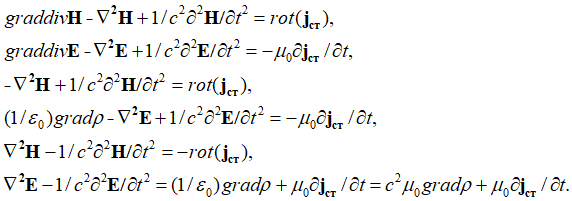, (8)

Однако мы видим, парадокс того, что здесь присутствует плотность электрического заряда . Но в среде распространения электромагнитной волны реальных зарядов, а также и реальных токов быть не может. Этот парадокс попытались решить, и физики. С этой целью они были вынуждены ввести не только электрические сторонние заряды и токи, но и магнитные сторонние заряды и токи [6, с. 34], и общие уравнения Максвелла для среды распространения приобрели вид:

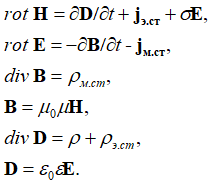, (9)

При этом соответственно по логике физики вводится зависимость тока от напряженности стороннего поля [7, с. 18] в среде распространения. Следовательно, для описания вывода электромагнитной волны в среде распространения при исключении реальных токов и зарядов с учетом сторонних токов и зарядов имеем [8, с. 116]:

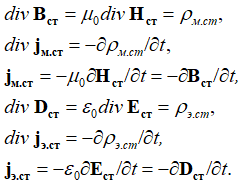, (10)

Отсюда уравнения Максвелла для среды распространения электромагнитной волны с учетом того, что уже было сделано до нас, можно представить в виде:

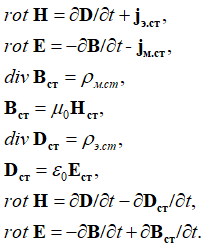, (11)

В этом случае волновые уравнения приобретают вид:

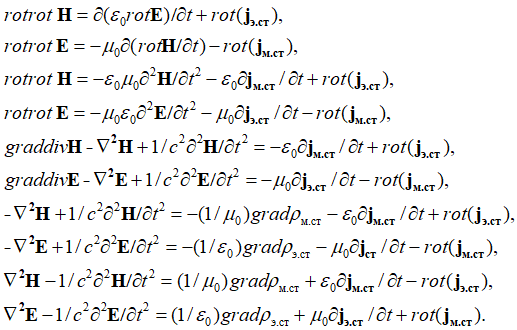, (12)

Таким образом, мы получаем, что образование волнового вида как электрических, так и магнитных составляющих зависит от суммы сторонних электрических и магнитных зарядов и токов в среде распространения. При этом если для волны магнитного поля мы имеем разность членов вида и , то для волны электрического поля уже присутствует сумма членов вида и . Это фактически можно интерпретировать тем, что сложение в одной противоположности означает вычитание в другой противоположности. Физически это означает замкнутый процесс между противоположностями, и это фактически было введено физиками до нас. Соответственно остается дать физическую интерпретацию этих сторонних зарядов и токов, что мы сделаем несколько ниже. Однако не надо думать, что это все наши придумки, аналогичный вид был получен только в комплексном виде на основе векторных потенциалов и с взятием производной по времени в [9, с. 40]:

, (13)

На основании (12) с учетом мы можем сделать следующие преобразования:

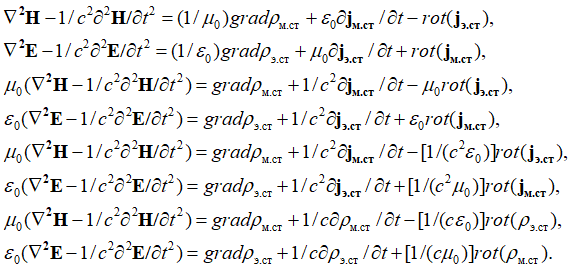, (14)

В этом случае магнитная и электрическая индукция волновых процессов выражается через магнитные и электрические сторонние заряды. Понятно, что вид уравнений (11), фактически интуитивно сделанный до нас, означает отказ от известных обычных уравнений Максвелла с токами и зарядами в нашей системе наблюдения для перехода к волновым свойствам из-за наличия парадоксов. Собственно эти парадоксы уже прослеживались на уровне обычных уравнений Максвелла, связанных с законом Фарадея:

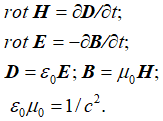, (15)

Суть парадокса в том, что первые два уравнения противоречат известному уравнению непрерывности и уравнению Умова-Пойтинга вида [10, с. 44]:

, (16)

То есть, по первым двум уравнениям (15) получается, что изменение во времени не может давать изменение по пространству в силу замкнутости из-за операции ротора (rot), и это при однозначной связи напряженностей полей с энергией. Собственно, это означает чудеса, так как изменение по времени должно превратиться ноль. Если же предположить, что при операции ротора (rot) дифференциальные члены, при вычитании, друг другу не равны (а это, кстати, используется при переходе к волновым уравнениям по Фейнману в [11, с. 129]), то уравнения Максвелла переходят в уравнения непрерывности. В этом случае говорить о наличии уравнений Максвелла с использованием операции (rot) нет смысла, то есть это отрицает и закон Фарадея. В уравнении Умова-Пойтинга (15) соблюдается закон сохранения количества, что означает, что для соблюдения закона Фарадея в обычных уравнениях Максвелла необходимо иметь еще один дополнительный член до получения уравнения непрерывности с сохранением количественных соотношений. Этот дополнительный член физики и ввели на практике, назвав его сторонним (фиктивным) током, который связан со сторонним зарядом или напряженностью стороннего электрического (магнитного) поля. Если мы начнем расписывать полученные уравнения Максвелла (11) по координатам на основании того, что уже было сделано до нас, то получим вид:

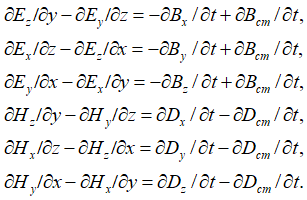, (17)

Однако члены вида , , должны выражаться через реальные величины, которые следуют из законов физики. Кроме того, здесь получается или двузначность образования замкнутых напряженностей полей в виде ротора в зависимости от времени составляющих и , а также и , или в случае представления , , в качестве реальных величин должна быть моментальная компенсация в силу необходимого равенства. Если учесть пространственно-временной континуум по неотделимости длины и времени друг от друга в соответствии с СТО и ОТО Эйнштейна, то это означает, что наряду с наличием напряженностей электрических и магнитных составляющих на координаты длин по трем осям х, у и z, должна существовать и проекция напряженностей электрических и магнитных полей на время t, так как иное означает независимость пространства и времени от электромагнитных составляющих, что не наблюдается.

Кроме того, в уравнениях Максвелла при исключении неоднозначности проекций на координаты длины, остается только проекция электромагнитных составляющих на время, что позволяет одновременно связать однозначно электромагнитные составляющие с пространственно-временным искривлением по СТО и ОТО Эйнштейна (что не догадался сделать Эйнштейн при попытке получить теорию единого поля). Собственно проекцию на время ввел еще и Фейнман для векторных потенциалов [12, с. 271], для связи с СТО и ОТО Эйнштейна. Однако он не понял, что при однозначной связи электромагнитных составляющих с векторными потенциалами такие же проекции на время должны быть и для электромагнитных составляющих, так как иначе не будет однозначной связи.

Отсюда уравнения (17) с учетом пространственно-временного континуума необходимо переписать в виде:

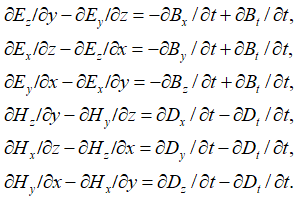, (18)

При записи уравнений Максвелла в виде (18) нет неоднозначности, связанной с двойным использованием напряженностей полей по координатам длины. При этом учитывается необходимость пространственно-временного континуума из-за наличия проекций на время. Однако мы при такой записи не избежали парадокса, при котором пути действия и противодействия совпадают, так как справа от знака равенства изменения происходят по одной переменной – времени, с видом , . Получается замкнутость с обнулением по одной переменной – времени, вместо замкнутости по окружности. Иными словами, вновь не соблюдается закон Умова-Пойтинга, когда изменения по времени должны давать изменения по пространству. То есть, зафиксировать изменения по времени с компенсацией членов, нет возможности. Слева и справа в (17) от знака равенства мы имеем замкнутый вид в общей системе наблюдения, как по времени, так и по пространству, но слева от знака равенства обнуления нет, так как есть замкнутое движение по двум координатам длины. Для решения этого парадокса справа от знака равенства вспомним геометрию Минковского, которая однозначно связана с СТО и ОТО Эйнштейна в силу преобразования длины на время, и наоборот, r=ct [13, с. 226]. Это означает связь длины и времени как противоположностей через скорость света. Поэтому уравнения (18), с учетом необходимости отображения любого объекта по всем четырем координатам (иначе это дает отсутствие связи объекта с пространством и временем) надо переписать в виде:

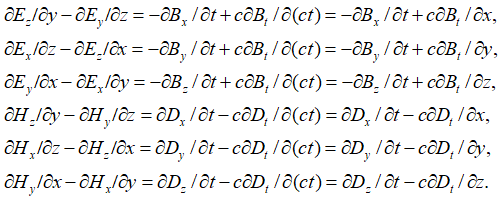, (19)

В этом случае замкнутому движению по окружности по двум координатам длины соответствует и противодействует замкнутое движение по окружности по оставшейся координате длины и координате времени. Таким образом, уравнения вида: , характеризуют преобразования электромагнитных компонент в пространстве и времени с учетом закона сохранения количества в соответствии с СТО и ОТО Эйнштейна. Однако в данной записи величины констант магнитной проницаемости и электрической проницаемости при взаимодействии (иначе бы в уравнении они бы не существовали) представляют собой объект мироздания от среды распространения. Иными словами, объекты среды распространения только тогда являются реальными корпускулярно-волновыми объектами, когда есть реальные величины для их выделения от иных представлений. Это должно найти отражение в уравнениях (19). Понятно, что по правилам математики в уравнениях (19) мы не имеем нарушений и при переходе на числовые значения 3-3=5-5=0. Однако в физике это означает исчезновение объектов, а объективная реальность исключает исчезновение и выражается в том, что при вычитании происходит преобразование из корпускулярного вида в волновой, и наоборот. Подтверждением этому является аннигиляция электрона и позитрона и превращение фотона (при столкновении с препятствием) в электрон и позитрон. Учитывая эту разницу между математикой и физикой в [14, с. 5-37] на основе нашей теории мироздания, мы показали, что, корпускулярно-волновой дуализм любого объекта отображается на основе общей формулы мироздания:

, (20)

Здесь, сложение в одной противоположности должно выражаться вычитанием в другой противоположности со сменой закономерностей при условии закона сохранения количества в противоположностях при взаимном обмене. Иначе будет чудо возникновения или исчезновения в ноль, или будет одна и та же противоположность, так как нет различий. Одновременно, так как любой объект мироздания должен выражаться через противоположности мироздания, то это исключает представление объекта только в действительных числах, в силу того, что смена закономерностей в противоположностях осуществляется за счет атрибута принадлежности в виде мнимой единицы (i=(-1)^1/2). При этом, закономерности, при смене знака за счет атрибута принадлежности мнимой единицы (i=(-1)^1/2), должны меняться, с условием закона сохранения количества как нами показано в [14, с. 5-37]. Некоторые читатели могут подумать, что приравнивание действительной части к мнимой части – это наша выдумка. Однако в квантовой механике давно известно равенство iФ=А₄=A_t, при А₁=A_х, А₂=A_у, А₃=A_z, а также связь двух противоположностей длины и времени вида x=ict [15, с. 317]. Более того при «линеаризации» формулы энергии Эйнштейна с переходом к системе уравнений Дирака также в этих уравнениях присутствует равенство действительных и мнимых составляющих в числовом представлении компонент импульсов. Отсюда следует вывод, что объект мироздания должен выражаться в комплексном виде, что означает его представление в противоположностях с исключением исчезновения за счет преобразования составляющих из корпускулярного вида в волновой вид, и наоборот. Собственно комплексный вид уравнений Максвелла ввели на практике также до нас, через комплексную электрическую и магнитную проницаемость [16, с. 117-189], что соответствует корпускулярно-волновому дуализму объектов мироздания. Оставалось только признать очевидное, это наличие проекций электрических и магнитных составляющих на время, так как отделить длину и время невозможно в силу наличия пространственно-временного континуума. Соответственно покажем вывод усовершенствованных уравнений Максвелла на основе наличия комплексной магнитной проницаемости.

Берем известное обычное уравнение Максвелла в частных производных в виде:

, (21)

При представлении в электродинамике значения магнитной проницаемости в комплексном виде, что, кстати, позволяет решить проблему изменения направления движения по принципу Гюйгенса-Френеля в силу взаимодействия со средой распространения, имеем:

, (22)

Здесь i=(-1)^1/2. При подстановке получаем:

, (23)

То есть классическая электродинамика при допущении наличия комплексных значений электрической и магнитной проницаемости потребовало и комплексный вид для уравнений Максвелла с наличием комплексных волновых электромагнитных функций. Здесь значение одинаковой величины в действительной и мнимой части, так как среда не изменяет объект, движущийся со скоростью света, и сама не изменяется при взаимодействии. Собственно, это отражается через принцип Гюйгенса-Френеля при использовании так называемых вторичных источников излучения с соблюдением закона сохранения количества. В противном случае объект исчезает в ноль или будет расти до бесконечности из нуля, в силу отсутствия закона сохранения количества. Иными словами, среда характеризует взаимодействие без изменений при сохранении в ней движущегося объекта. То есть, мы при условии закона сохранения количества и неизменности среды распространения имеем:

, (24)

Здесь мнимая единица i выступает как атрибут противоположности и фактически выражает закон, по которому на действие одной противоположности происходит противодействие, что и выражается возвратом со знаком минус при двойном изменении. Равенство действительной и мнимой части также не наша выдумка, и как будет показано ниже, следует из вида уравнений в системе Дирака. Собственно приравнивание А₄ к проекции на время A_t также было сделано в электродинамике Фейнманом [12, с. 271]. Однако хоть мы и придали для различия в (23) составляющих мнимую единицу, но путь изменения в зависимости от времени остался одинаковым. В этом случае составляющие могут только одновременно расти или убывать в силу одинаковых закономерностей и необходимости соблюдения равного количественного соотношения. Здесь нет взаимодействия через обмен, за счет преобразования по противоположностям длины и времени в соответствии с СТО и ОТО Эйнштейна. Поэтому, не нарушая вида уравнения, мы умножаем числитель и знаменатель мнимой производной на скорость света:

, (25)

С математической точки зрения при исходном уравнении (23) ничего не поменялось, а с физической точки зрения мнимая производная отражает противоположность, где за счет скорости света длина и время меняются местами. Иначе при сохранении одинакового вида представления объектов при разнице в скорость света нет отличий, и это исключает наличие противоположностей. Отсюда и смена функций при переходе в противоположную систему наблюдения. При этом, на основе преобразований Лоренца-Минковского, время однозначно преобразовывается в длину, а длина меняется на время в равных количествах в соответствии с СТО и ОТО Эйнштейна, аналогично и составляющие полей, что и было подмечено Фейнманом для векторных потенциалов. Ему оставалось лишь только признать наличие проекций на время для электромагнитных составляющих, что вытекало из однозначной связи векторных потенциалов с электромагнитными составляющими, но он этого не понял и посчитал, что это не так, о чем сказал в [12, с. 271]. Собственно, это заблуждение на самом деле связано с тем, что он исходил из отсутствия электромагнитного происхождения массы частиц, так как считал, что для этого необходимы дополнительные сдерживающие силы. Однако как будет показано ниже, если считать функции в системе уравнений Дирака не вероятностными функциями, а электромагнитными функциями, то никаких сдерживающих сил при переходе от волнового вида к корпускулярному виду не требуется.

Отметим также, что выражение процесса по Фарадею вида:

, (26)

Не может отражать ни один реальный объект, так как нет зависимости процесса по координате z. То есть, в этом случае объект, характеризуемый через процесс (20), не был бы связан с нашим мирозданием, а это элемент чуда. Отсюда имеем:

, (27)

Одновременно данный вид соответствует элементарному объекту мироздания, когда процесс в левой части уравнения (27) характеризует разомкнутость на противоположность по времени , в силу невозможности наблюдать проекцию на время, а процесс, справа от нуля уравнения (27) замкнутость объекта. Таким образом, объект мироздания взаимодействует с другими объектами благодаря не наблюдаемому в пространстве члену , и имеет необходимую замкнутость для своего отдельного существования, исходя из наличия операции ротора (rot). Надо отметить, что в противоположности замкнутость (rot) по координатам длины переходит в замкнутость по оставшейся координате длины и времени, и наоборот. Понятно, что меньше 4-х составляющих в уравнении (27) при описании объектов мироздания иметь нельзя, так как приходим к парадоксам. Отсутствие одинакового вида дифференциальных членов для магнитных и электрических составляющих говорит о представлении их как противоположностей. Одновременно вид уравнения (27) может быть выражен в базисном разложении в соответствии с общей формулой мироздания, так как в противном случае он оказывается независимым объектом, замкнутым сам на себя. Действительно в соответствии с [14, с. 5-37] при необходимом базисном разложении через функции (иначе закон мироздания (20) не получить), мы можем представить, что , , , , , , , . Понятно, что вид уравнения (26) по закону Фарадея не может дать соответствие с формулой мироздания (20) при представлении через функции. Это значит, что не отражается ни один реальный объект мироздания, так как не выполняется условие, при котором сложение в одной противоположности должно выражаться через вычитание в другой противоположности. В противном случае мироздание не замкнутая система с наличием чудес, а объекты без наличия замкнутости в принципе бы не существовали. Надо отметить, что представление компонент дифференциального уравнения (27) через соотношения Эйлера были сделаны до нас. С этой целью в системе уравнений Дирака были использованы волновые функции Ψ, которые характеризовали вероятность. Одновременно, если считать координаты длины и времени не подчиняющимися преобразованиям Лоренца – Минковского (гиперболические синус и косинус, с переходом в синус и косинус при смене системы наблюдения за счет мнимой единицы), то получается система координат по геометрии Эвклида, что не соответствует замкнутой системе мироздания. Собственно иная интерпретация дифференциалов без представления через указанные закономерности не даст равенства при преобразовании и объект либо исчезнет, либо будет расти до бесконечности в одной из противоположностей. Иными словами уравнение (27), которое практически интуитивно было введено в электродинамику физиками исходя комплексных значений электрической и магнитной проницаемости, соответствует математическому равенству, если при этом исключается линейность координат длины и времени по геометрии Эвклида. Таким образом, наши оппоненты пытаются опровергнуть то, что уже давно интуитивно было введено в электродинамику. Отличие в том, что мы показали логическую цепочку рассуждений, которые приводят к виду уравнений (27), с исключением иных представлений.

Отсюда имеем вид усовершенствованных уравнений Максвелла по координатам:

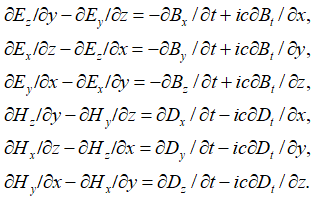, (28)

Есть также и комплексно-сопряженный вариант. Отметим, что к аналогичному виду уравнений, только на базе волновых функций, характеризующих вероятность, пришли и физики, когда в системе уравнений Дирака приравняли массу покоя к нулю и стали характеризовать полученные уравнения в виде нейтрино и антинейтрино (это мы рассмотрим несколько ниже). Иными словами, мы ничего не придумывали, все уже было практически сделано до нас. Еще раз отметим, что отсутствие проекций электромагнитных составляющих на время дало бы неоднозначность от использования только проекций по координатам. Таким образом, необходимость перехода к усовершенствованным уравнениям Максвелла от обычных уравнений Максвелла связано с необходимостью:

1. Использования сторонних токов и зарядов для описания свойств электромагнитной волны.
2. Соответствия электромагнитных составляющих преобразованиям Лоренца - Минковского, с подчинением пространственно-временному континууму по СТО и ОТО Эйнштейна за счет проекций электромагнитных составляющих на время:
3. Соблюдения соответствия с общей формулой мироздания (20), и представление объектов через противоположности в соответствии с закономерностями в (20) в корпускулярно-волновом виде, так как иное соответствует чудесам.
4. Представления электромагнитных составляющих в комплексном виде, с использованием в усовершенствованных уравнениях Максвелла мнимой единицы. Это как это будет показано в дальнейшем, позволяет обеспечить переход от волновых свойств к корпускулярным свойствам на основе реальных электромагнитных функций, и дает реальность выполнения таких физических процессов через реальные частицы – электронные и мюонные нейтрино (антинейтрино).

Собственно, мы видим, что фактически усовершенствование коснулось только учета того, что уже давно было практически введено в физику, но не было записано в соответствующем виде в общем уравнении. Даже необходимость комплексного вида волновых электромагнитных функций также вытекала из использования комплексных значений констант электрической и магнитной проницаемости, что характеризует среду распространения как корпускулярно-волновой объект.

Однако мы видим, что усовершенствованные уравнения Максвелла исключают наличие реального тока и зарядов, и более того, эти токи и заряды были исключены самими физиками для электромагнитной волны в среде распространения. Но данное исключение не означает исчезновение из реальности токов и зарядов, а связано с тем, что их наличие получается на основе усовершенствованных уравнений Максвелла при взаимодействии. Покажем это.

Так последние уравнения в (12) могут быть переписаны с учетом того, что [3, с. 119; 4, с. 300] как:

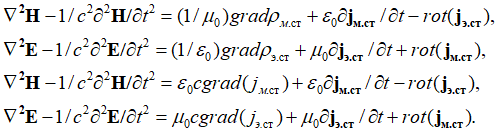, (29)

Подчеркнем, что такая запись в векторном виде не является совсем корректной, так как не учитывает разложение составляющих по координатам длины и времени. Но данная векторная запись означает, что электромагнитные составляющие в среде распространения формируются за счет сторонних токов. Однако теперь остается определить, что физически собой представляют сторонние электрические и магнитные токи. Надо отметить, что векторная запись уравнений также не позволяет понять необходимость корпускулярно-волнового дуализма, и здесь не видна необходимость использования комплексных функций, но более краткой формы записи, помимо векторной записи – нет. Поэтому, при наличии усовершенствованных уравнений Максвелла с исключением неоднозначности и соблюдения корпускулярно-волнового дуализма, мы должны уравнения (29), с учетом необходимости мнимой составляющей, отражающей проекцию на время, переписать в виде:

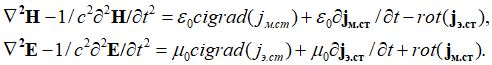, (30)

Легко заметить, что справа от знака равенства уравнения (30) соответствуют усовершенствованным уравнениям Максвелла (28), если сделать замену переменных сторонних токов на электромагнитные составляющие и считать, что, при выбранной системе наблюдения, значений слева от знака равенства не существует в силу соблюдения равенства изменений по длине и времени. Это верно для плоской волны, движущейся со скоростью света. Фактически сторонние токи являются эквивалентами напряженностей электрических и магнитных полей при варианте отсутствия взаимодействия. Более того, как показано в [17, с. 10-24] и будет показано несколько ниже, усовершенствованные уравнения Максвелла являются реальными объектами, и в соответствующей системе наблюдения отражают электронные и мюонные нейтрино (антинейтрино), чего не скажешь об обычных уравнениях Максвелла. Иными словами, получается, что формирование электромагнитной волны происходит за счет взаимодействия пары электронных и мюонных нейтрино (антинейтрино). Так как в данном случае в (30) взаимодействие существует, то при взаимодействии происходит переход в противоположность. Отсюда, слева от знака равенства мы имеем отображение электромагнитных составляющих, характеризующих кинетическую энергию, а справа от знака равенства представление потенциальной энергии в виде объектов среды распространения за счет изменений (движения) по координатам и времени в соответствии с СТО и ОТО Эйнштейна. То есть сторонние электрические и магнитные заряды выступают как объекты среды распространения от противоположностей длины и времени и аналогичны положительным и отрицательным зарядам. Конечно, многие оппоненты могут подумать, что это наши выдумки. Однако еще Фейнман в [18, с. 273] при доказательстве относительности магнитных и электрических полей рассматривал подчинение плотности положительных и отрицательных зарядов в соответствии с изменением длины и времени по СТО и ОТО Эйнштейна в виде:

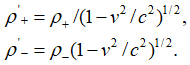, (31)

Иными словами, плотности положительных и отрицательных зарядов ведут себя аналогично тому, как ведут себя длина и время в СТО и ОТО Эйнштейна. Разница лишь в обозначении. Собственно, на основании равенств (31) получается в [18, с. 273] связь силы Кулона (электрическая сила) с силой Лоренца (магнитная сила) в соответствии с преобразованиями Лоренца:

, (32)

В [14, с. 5-37] мы показали, что такая зависимость, соответствующая преобразованиям Лоренца, характеризует данные силы как противоположности с подчинением замкнутой системе мироздания в виде окружности с сохранением количества. А это означает, что силой противодействия к силе Кулона является сила Лоренца, которая формируется от противоположности. Однако в [18, с. 273] рассматривались реальные заряды, а в среде распространения, зарядов, а также их движения нет. При этом соблюдается условие относительности электрических и магнитных полей. Напомним, что среда распространения может характеризоваться только через пространственно-временное искривление по СТО и ОТО Эйнштейна и отражает потенциальную энергию. В электродинамике среда распространения (а значит и объекты среды) выражена через константы электрической и магнитной проницаемости. Понятно, что, чтобы электрическая и магнитная проницаемость отражали реальные процессы в мироздании, они должны быть представлены через пространство и время, так как в ином случае мы имеем их независимость от пространства и времени, и тогда выявить наличие таких констант в мироздании было бы невозможно. Собственно такую ошибку совершили физики, когда стали представлять массу частиц, как нечто отдельное от пространства и времени без наличия закона взаимосвязи. Действительно для определения констант электрической и магнитной проницаемости в пространстве и времени нужно иметь законы их взаимодействия, а при независимости их нет. Это определяет необходимость выражения электрической и магнитной проницаемости через пространственно-временное искривление в соответствии с ОТО Эйнштейна. Причем значение скорости в (31) отражает как бы проекцию на время (это не понял Эйнштейн), что обеспечивает наличие отсчета в абсолютной системе наблюдения, связанной с нашей системой наблюдения через скорость света. В этом случае константы электрической и магнитной проницаемости имеют вид:

, (33)

Здесь скорость v_пр – характеризует обобщенную среднюю интегральную скорость в противоположности в соответствии с кинетической энергией.

Иными словами, константы электрической и магнитной проницаемости среды распространения определяются исходя из общей кинетической энергии в глобальной противоположности.

С учетом того, что сторонние токи и заряды связаны соотношением [3, с. 119; 4, с. 300], получается, что формирование электромагнитных полей в среде распространения определяется пространственно-временным искривлением. Отсюда имеем:

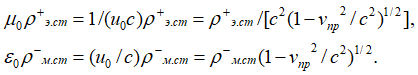, (34)

В этом случае произведение величин в (34) инвариантно и соответствует произведению констант электрической и магнитной проницаемости. Соответственно, если рассматривать объект среды распространения в виде противоположностей через длину и время с подчинением СТО и ОТО Эйнштейна как эквиваленты соответствующих сторонних противоположных зарядов, то тогда сторонние заряды отражают связь кинетической и потенциальной энергии через значение с². Иными словами необходимо сделать нормировку для отображения сторонних зарядов в системе наблюдения от среды распространения в одинаковом виде . Кроме того, так как сторонние электрические и магнитные заряды в (9) это противоположности, то соответственно мы должны это учесть в виде разницы в знаках при отражении через числовые значения. То есть: , . В итоге при суммировании для отображения электрических и магнитных составляющих волны, формируемых объектом среды распространения, мы имеем:

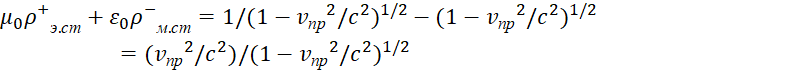, (35)

Как это будет показано несколько ниже, сторонние электрические и магнитные заряды имеют однозначную связь с волновыми процессами, которые отражают электрическую и магнитные составляющие. Далее мы учитываем, что магнитные и электрические силы имеют однозначную связь при взаимодействии обычных зарядов в виде [19, с. 119]:

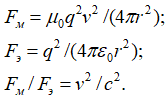, (36)

Отсюда при отображении этих реальных зарядов при движении в противоположной системе наблюдения в нашей системе наблюдения v=v_пр.

В итоге имеем:

, (37)

При этом соблюдается относительность между магнитными и электрическими составляющими, что соответствует электромагнитному континууму. Иными словами сторонние заряды в нашей системе наблюдения через константы электрической и магнитной проницаемости отражают движение реальных зарядов, отражающих объекты длины и времени, но в противоположной системе наблюдения, что характеризуется через скорость v_пр. Исходя из (37) следует, что объекты среды распространения, как реальные объекты характеризуются через силовое воздействие в виде магнитной и электрической силы с учетом движения реальных зарядов в противоположности. Надо отметить, что представление констант электрической и магнитной проницаемости через пространственно-временное искривление позволяет решить проблему разницы масс между электроном и протоном, что нами показано в [20, с. 12-32] и будет показано ниже. Это связано с тем, что кинетическая энергия в первой системе наблюдения выглядит как потенциальная энергия, в системе наблюдения связанной с первой через скорость света. Таким образом, получается, что источником наличия электромагнитных волн является пространственно-временное искривление среды распространения в соответствии с (30). При этом в противоположной системе наблюдения пространственно-временное искривление среды с наличием излучения (поглощения) электромагнитных волн характеризуется через движение электрона вокруг протона, что и дает отличие между константами электрической и магнитной проницаемости за счет кинетической энергии в противоположности. Понятно, что разница масс между протоном и электроном является препятствием для аннигиляции так называемых противоположных зарядов. Соответственно обеспечивается динамическое равновесие при обмене между противоположностями, чего получить при одинаковом представлении кинетической энергии в противоположностях было бы невозможно. Оппоненты могут подумать, что представление пространства и времени как источника излучения и поглощения электромагнитных волн это наша выдумка. Однако это не так. В квантовой механике [21, с. 352] давно введено понятие электромагнитного вакуума с наличием виртуальных фотонов. Мы лишь представление в чудесах заменили реальным обоснованием. То есть нашли источник формирования электромагнитных волн в среде распространения на основе констант электрической и магнитной проницаемости (характеризуются через пространственно-временное искривление среды), которые получаются на основе кинетической энергии в противоположности. Это, кстати, позволило решить проблему исключения падения электрона на протон при его движении по орбите, так как восполнение энергии происходит за счет магнитных и электрических сил, формируемых на основании кинетической энергии от противоположности, представленной через константы электрической и магнитной проницаемости. Иными словами, излучение в нашей системе наблюдения имеет баланс с излучением в противоположности. Таким образом электромагнитные составляющие в одной противоположности характеризуются через пространственно-временное искривление в противоположности.

Для развития этой темы, в плане формирования электромагнитных составляющих от среды, мы рассмотрим использование в электродинамике векторных потенциалов, которые как бы определяют статику электрических и магнитных составляющих в среде, то есть характеризуют объекты среды распространения.

Собственно, с помощью векторных потенциалов А и Ф было фактически узаконено применение проекции электромагнитных составляющих на время, что было интуитивно предложено в электродинамике через дополнительные закономерности связи с электромагнитными составляющими.

Здесь замкнутые величины неких вспомогательных функций А и Ф в динамике изменения стали представлять в виде величин (то есть, объектов) неизменных во времени и пространстве через напряженности магнитного и электрического поля в соответствующей противоположной системе наблюдения.

Причем векторный потенциал А должен был удовлетворять условию (это и есть неизменность по пространству), что достигалось посредством следующего уравнения [22, с. 118]:

, (38)

По сути, величина магнитного поля В представляется константой от rot А. В физике это эквивалент формулы . В этом случае мы имеем, при нормировке на величину В, формулу , и она при условии равенства возможна только при наличии закономерностей по формуле мироздания (20) справа от знака равенства. Подстановка этого выражения в уравнение 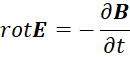дает уравнение:

, (39)

Собственно (39) это уравнение Максвелла, выраженное через новую переменную А, так как мы можем записать:

, (40)

Однако как мы ранее подчеркивали, данный вид противоречит уравнению Умова-Пойтинга (16). Чтобы удовлетворить уравнению (39) без парадоксов, выражение в скобках от (39) приравнивалось к величине отрицательного градиента потенциальной функции , то есть имеем уравнение:

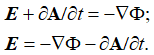, (41)

Иными словами, за счет использования векторных потенциалов физики сами отказались от обычных уравнений Максвелла. При нормировке (41) на Е, с учетом того, что величина Е отражает противодействие величине В через знак минус как противоположности, мы получаем, что для выполнения равенства необходимо использовать закономерности слева от знака равенства по формуле мироздания (20). То есть, в электродинамику еще до нас ввели интуитивно закон для любых объектов мироздания, соответствующей формуле (20), так как иначе бы объект, автоматически, становился независим от нашего мироздания. По сути, выражение (41) отражает, что Е как замкнутая величина по (38) также не изменяется. Далее, с учетом известного в электродинамике равенства Н=сЕ (а это закон связи противоположностей через скорость обмена, которая равна скорости света), мы при замене электромагнитных составляющих на уравнения векторных потенциалов, что соответствует смене системы наблюдения на противоположную систему, имеем:

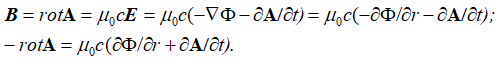, (42)

Фактически мы имеем закон в динамике изменения через новые переменные в виде векторных потенциалов. Затем мы учитываем известную формулу из электродинамики [23, с. 165]:

, (43)

В (42) рассматривается динамика взаимодействия противоположностей (иное вообще исключает возможность преобразований), а она происходит со скоростью света. Соответственно мы принимаем, что v=c, так как вариант формулы (43) соответствует рассмотрению процессов движения в одной общей системе наблюдения координат. То есть, векторные потенциалы при соблюдении закона взаимодействия связаны так же, как компоненты электрического и магнитного поля с учетом аналогичного уравнения Н=сЕ, и характеризуют именно волновое электромагнитное поле, но в противоположной системе наблюдения. Собственно такое соотношение сА=Ф следует из полученных физиками волновых уравнений Даламбера, что будет показано нами несколько ниже. То есть, и здесь нет наших выдумок. Соответственно для значений Е и Н не остается иного физического аналога кроме как времени и пространства (при наблюдении из противоположности), которые тоже связаны при условии соблюдения ОТО (а это закон сохранения количества) по преобразованиям Минковского в виде r=ct. Учитывая, что векторное отображение не определяет ортогональности противоположностей, какими являются А и Ф, которые аналогичны Е и Н, мы должны уравнение (42) расписать по координатам, то есть представить в виде количественных значений по четырем составляющим двух глобальных противоположностей, например:

, (44)

Иными словами, для векторного потенциала Ф при проекции на координату длины также не остается иной проекции как на время в уравнении по частным производным (44) Другими словами, мы получили фактически соответствие ротора и уравнения непрерывности с учетом проекции на время на основе вектор – потенциалов. Такая форма записи соответствует общей формуле мироздания (20), если учесть, что параметры дифференциалов могут быть только закономерности, так как иначе не выполняется закон сохранения количества для любого объекта. Иными словами, исключается линейность изменения дифференциалов, так как это соответствует геометрии Эвклида с отсутствием СТО и ОТО Эйнштейна. Таким образом, мы исключили парадокс классических обычных уравнений Максвелла, так как имеем замкнутость (закон сохранения количества) по противоположностям. Повторим еще раз, что для производной по величине х для вектора – потенциала Ф в (44) не остается иных компонент, кроме как проекции Ф на время, то есть Ф_t . Это аналогично тому, как это было сделано Фейнманом в [12, с. 271]. Здесь надо заметить, что электрические и магнитные составляющие однозначно связаны в законах Фарадея и Био-Савара с реальными объектами, а эти объекты подчиняются преобразованиям Лоренца-Минковского, с наличием проекции на время. Если бы электрические и магнитные составляющие не имели бы проекцию на время, то о связи реальных объектов с электромагнитными процессами можно было бы забыть из-за независимости, и в этом случае нет закона их связи. Далее, с учетом применения векторных потенциалов в квантовой механике [15, с. 317], значение проекции на время должны умножить на мнимую единицу i (собственно, это отражение того, что проекция на длину и время это противоположности). По сути, переходим к комплексному виду, то есть выражаем любой объект в виде противоположностей в одной из систем наблюдения. Такое умножение на мнимую единицу связано и с получением соответствия с уравнениями Дирака при линеаризации (это мы покажем несколько ниже), которые получены из уравнения энергии Эйнштейна. Суть такого применения ‒ совместить волновые свойства с корпускулярными свойствами по закону преобразования определяемого мнимой единицей (i=(-1)^1/2) с условием формирования противодействия на действие, что было сделано Шредингером и Дираком. В противном случае независимость уравнений по волновым и корпускулярным свойствам, так как только мнимая единица обеспечивает смену закономерностей по формулам Эйлера. Без наличия мнимой единицы получить преобразование уравнений Максвелла в преобразования Лоренца-Минковского (а это необходимое условие связи волновых и корпускулярных свойств), с соблюдением закона сохранения количества по аргументам функций, не представляется возможным. В итоге имеем вид аналогичный усовершенствованным уравнениям Максвелла (28):

, (45)

Иными словами, через векторные потенциалы, путем исключения парадокса обычных уравнений Максвелла по (40), физики интуитивно уже сами фактически усовершенствовали уравнения Максвелла и признали наличие противоположной системы наблюдения, и разница фактически была только в обозначении переменных. Понятно, что нет никакой необходимости вводить дополнительно векторные потенциалы, если они не отражают реальных процессов, в данном случае в противоположности. При этом, так как Ф=сА, а Н=сЕ, то Ф в противоположной системе наблюдения эквивалентна магнитной компоненте Н, а А в противоположной системе наблюдения это аналог электрической компоненты Е. Соответственно для значений Е и Н в противоположной системе наблюдения отводится роль компонент длины и времени, то есть они описывают пространственно-временное искривление (это кстати будет показано несколько ниже).

Для перехода к волновому виду векторных потенциалов физики вносят уравнения (38) и (41) в первое уравнение Максвелла вида из (11):

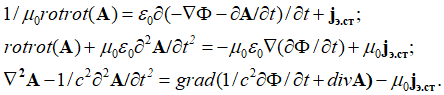, (46)

Далее физики налагают дополнительное условие (калибровка Лоренца) вида:

, (47)

Понятно, что физики тем самым узаконили правило, при котором смена переменных дифференцирования из неравенства (41) превращается в равенство в виде уравнения непрерывности (47). А это фактически эквивалентно смене системы наблюдения, когда длина меняется на время, и наоборот. В итоге получается уравнение Даламбера относительно векторного потенциала А вида:

, (48)

Понятно, что отрицательный знак справа от знака равенства в (48) связан со знаком стороннего тока. Из калибровки Лоренца (47) с учетом (41) и пятого уравнения в (11) в виде получается второе уравнение для векторного потенциала Ф:

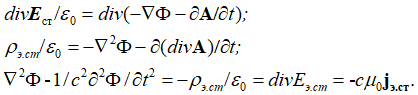, (49)

Мы видим, что последнее равенство в (49) переходит в равенство (48), если сА=Ф. Соответственно из последнего уравнения (49) с учетом () следует, что источником формирования волнового вида, является разница значений величины проекции на время (). Поэтому, в силу того что мы в пространстве не наблюдаем проекции на время, среда распространения имеет однородный вид. Из (48) и (49) следует, что векторные потенциалы, так же как и электромагнитные составляющие, характеризуют один и тот же волновой электромагнитный процесс, но в противоположных системах наблюдения от длины и времени. Надо отметить, что представление волновых уравнений векторных потенциалов через сторонние токи и заряды – это не наша выдумка, это было сделано физиками еще до нас в [3, с. 119]. Понятно, что если считать, что в среде распространения нет ни обычных зарядов, ни сторонних зарядов, то волновые уравнения векторных потенциалов вырождаются в плоские волны вида:

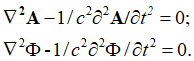, (50)

Это, собственно, определяет скорость распространения со скоростью света волновых процессов. Однако, при этом они становятся независимыми от среды распространения. В этом случае не соблюдается принцип Гюйгенса-Френеля, и мы не имеем необходимого для объектов корпускулярно-волнового дуализма. Иными словами, вновь приходим к парадоксу линейных изменений длины и времени по геометрии Эвклида, чего в физике быть не может. В последнем уравнении (49) можно считать, что начальное значение в соответствии с теорией Дирака [24, с. 349], так как значение заряда не входит в уравнение энергии Эйнштейна и определяет лишь направление движения. При этом понятие плотности заряда не имеет смысла (нет энергии под заряд, чтобы отобразить через силовое воздействие получающиеся изменения), и мы вновь приходим к отражению электромагнитных свойств через то, что реально существует - пространственно-временное искривление. Отсюда имеем:

, (51)

Это означает, что формирование волнового электромагнитного процесса в одной противоположности определяется кинетической энергией за счет движения в другой противоположности. Соответственно остается определить функции (Ф) уравнения (51) для решения в зависимости от знака стороннего тока или заряда (). Отметим еще раз, что для волновой функции, движущейся со скоростью света возможно только решение при отсутствии источника вторичного возбуждения в правой части от знака равенства () по уравнениям (50) в виде:

, (52)

Иными словами, для варианта уравнений (50) мы имеем наличие объекта, соответствующего всему мирозданию в полностью замкнутом виде. В реальности объекты внутри мироздания взаимодействую через обмен друг с другом, и при этом поглощение равно излучению. Именно такой случай и выражает уравнение (51). Понятно, что решение уравнения (51) возможно только в случае возрастающих или затухающих процессов при движении волны со скоростью света в виде:

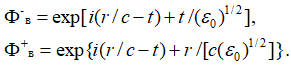, (53)

Это говорит о том, что в среде распространения не может существовать только одна волновая электрическая, либо волновая магнитная составляющая. Иными словами, существует один общий электромагнитный объект, в котором происходит обмен компонентами в соответствии с общей формулой мироздания (20) со сменой вида в зависимости от системы наблюдения и сменой закономерностей в соответствии с изменением аргумента функций за счет мнимой единицы с условием iх=w. В этом случае знак , определяет систему наблюдения от длины или времени, но в рамках представлений объектов среды распространения. При этом длина и время имеют противоположные знаки, что, кстати, связано с тем, что изменения по длине компенсируются изменениями по времени. Выше мы показали, что электрические и магнитные силы, которые, кстати, и определяют значения напряженностей электрических и магнитных полей, характеризуются связью по формуле (37). Понятно, что по нашей теории волновые процессы в одной противоположности выглядят корпускулярными в другой противоположности. Одновременно любой объект мироздания должен в любой системе наблюдения иметь представления, как в волновом, так и в корпускулярном виде, а это возможно, если обменные процессы между волновой и корпускулярной частью соответствуют друг другу в плане сохранения количества.

К такому же выводу о необходимости совмещения корпускулярных свойств и волновых свойств интуитивно пришли физики в [25, с. 30-31; 26, с. 298] в виде:

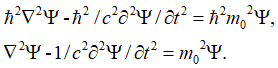, (54)

В этом случае мы имеем представление объекта Ψ в комплексном виде, что соответствует отображению в корпускулярно-волновом виде и в правой части уравнения.

В итоге для отображения корпускулярно-волновых свойств, с учетом принципа Гюйгенса – Френеля, уравнение (51) должно иметь вид:

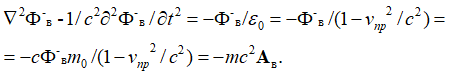
, (55)

Здесь учитывается, что по нашей теории m₀=1/c, а Ф=сА.

Иными словами, среда распространения характеризуется на основе константы электрической проницаемости в виде массы, определяющей волновой процесс. Это, кстати, соответствует гипотезе Луи де Бройля, как это будет показано несколько ниже. Далее отметим, что уравнение (48) и последнее уравнение (49) с учетом равенства вида отражают только одну составляющую электромагнитного поля в противоположности. Иными словами, не учитываются магнитные сторонние токи и заряды по (11). Это также было замечено физиками в [27, с. 36]. Отсюда был определен векторный потенциал для напряженности электрического поля вида:

, (56)

Одновременно для напряженности магнитного поля по аналогии должен быть вид:

, (57)

Далее, исходя из уравнения в (11) вида имеем:

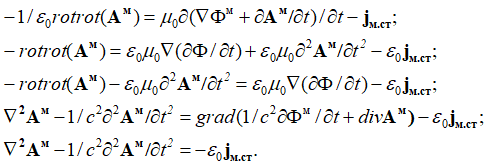, (58)

Аналогично для векторного потенциала Ф^м при находим:

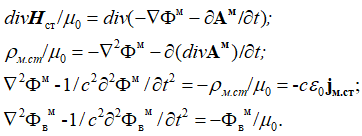, (59)

В этом случае решение будет иметь вид:

, (60)

Соответственно с учетом как электрических, так и магнитных сторонних зарядов, общие электрические и магнитные поля при выражении через векторные потенциалы в электродинамике представляются в виде сумм [28, с. 39]:

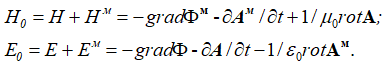, (61)

С учетом Ф=сА, и наличием мнимой единицы для проекций на время имеем:

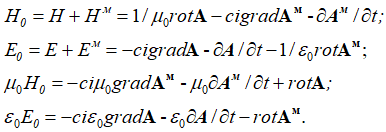, (62)

Кроме того, мы установили, что взаимодействие электрических и магнитных сторонних токов приводит к формированию электромагнитных волн по (30) в виде:

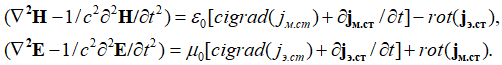, (63)

Если исходить из вида уравнений (55) и последнего уравнения в (59) с учетом представления в волновом виде и соблюдением принципа Гюйгенса-Френеля, то мы видим, что разница между (62) и (63) только в обозначении переменных: и . Отсюда, мы можем сделать запись вида:

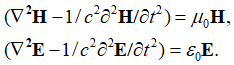, (64)

Практически это эквивалентно тому, что было сделано в электродинамике до нас в [9, с. 40] при получении уравнений (13) с той лишь разницей, что в нашем случае состояние среды при формировании электромагнитных волн оценивается на основе электрической и магнитной проницаемости.

Сравнивая (61), (62) и (63) следует запись уравнений:

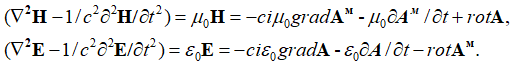, (65)

Понятно, что верхнее и нижнее уравнения в (65) отражают противоположности связанные через скорость света. С учетом приведения к противоположностям и при представлении констант электрической и магнитной проницаемости по (33), и отображении через векторные потенциалы в виде А и Ф, имеем:

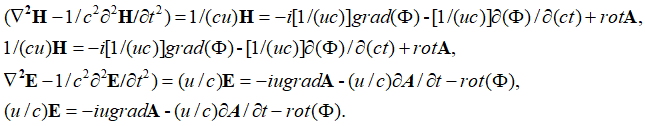, (66)

Соответственно для противоположностей имеем связь . Суть отличий для первого и второго уравнения (66) в том, что так как Е и Н отражают противоположности, то зависимость от скорости в противоположности через значение u=(с²-v_пр²)^1/2, выражается через обратно-пропорциональную зависимость.

Практически члены справа от знака равенства соответствуют членам усовершенствованных уравнений Максвелла, но в противоположной системе наблюдения. То есть, векторные потенциалы в противоположности отражают электромагнитные составляющие, что также было нами показано из подобия уравнений (28) и (30).

В результате мы видим, что усовершенствованные уравнения Максвелла не являются нашей выдумкой. Они выведены на основе исключения парадоксов обычных уравнений Максвелла и полностью соответствуют всем преобразованиям, сделанным в электродинамике. При этом необходимо отметить, что попытка добавления обычного тока , а также соответствующей плотности заряда в уравнения Максвелла (4) не позволяет обеспечить перехода в волновой вид, и физики также для этих целей были вынуждены использовать сторонние токи и заряды. Однако токи и заряды на основе электронов и позитронов существуют реально. Отсюда следует вопрос: «Как осуществляется переход к реальным частицам на основе усовершенствованных уравнений Максвелла?»

Понятно, что физики давно пытаются решить проблему перехода от волнового вида к корпускулярному виду для описания движения частиц. Например, в квантовой механике взаимосвязь перехода от кинетической энергии к потенциальной энергии движения частицы показана Дираком через «линеаризацию» формулы энергии Эйнштейна через систему уравнений Дирака [29, с. 295]. С этой целью были сделаны следующие преобразования формулы энергии Эйнштейна:

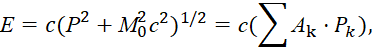, (67)

Здесь k изменяется от 0 до 3; P₀=M₀c; P₁=P_x; P₂=P_y; P₃=P_z. Из этой записи при использовании матриц для разложения (67):

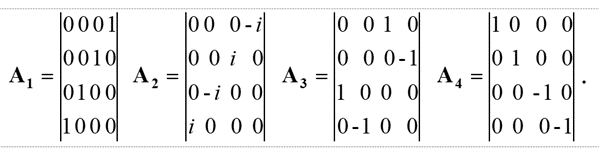(68)

Следуют известные уравнения, которые дают систему уравнений Дирака. При этом система уравнений имеет вид:

, (69)

Далее конкретные числовые значения заменяются дифференциальными операторами в виде:

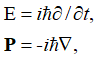, (70)

Которые должны воздействовать на волновую функцию Ψ, которая характеризует вероятность.

Понятно, что при «линеаризации» Дирак не опирался на реальные физические процессы для получения уравнения энергии Эйнштейна вида (67) и использовал функции, которые характеризуют вероятность вида:

, (71)

Так постоянная Планка ћ присутствует при дифференцировании во всех членах, то ее можно исключить из дальнейшего рассмотрения. Соответственно имеем вид функций при движении частицы без наличия внешних сил:

, (72)

При выражении одних функций через другие, с учетом дифференцирования для свободной частицы без внешнего электромагнитного поля, получаем:

, (73)

Далее выражаем одни функции через другие:

, (74)

На следующем этапе подставляем одни функции вместо других и сокращаем подобные члены:

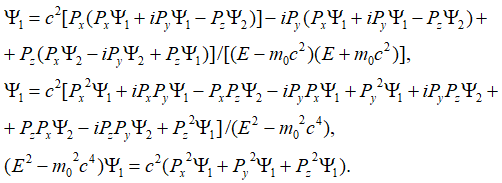, (75)

Сокращая на волновую вероятностную функцию, получаем уравнение энергии Эйнштейна в квадрате для взаимодействующих противоположных частиц:

(76)

Аналогичный результат мы имеем и для других волновых функций.

Таким образом, Дирак интуитивно показал, как можно перейти от уравнений волны в комплексном виде к отображению свойств корпускулярных частиц.

Однако Дирак не понял, что волновой вид функций Ψ должен отражать реальные электромагнитные функции, а не выдуманные волновые функции, характеризующие вероятность. Поэтому преобразование оказалось связано с чудесами. При этом выбрано ошибочное предположение «линеаризации», так как смысла взаимодействия при вероятности просто быть не может. Понятно, что Дирак, так же как и Шредингер, при выборе волновой функции Ψ с упором на вероятность опирался на функцию Луи де Бройля.

Изюминкой идеи Луи де Бройля, явилось то, что он учел взаимодействие кинетической и потенциальной энергии в любом объекте по замкнутому циклу (иначе объект бы распался). В соответствии с этим Луи де Бройль предложил свою формулу [30, с. 216], в которой со всякой неподвижной частицей массой (например, масса электрона) связан некоторый периодический процесс частоты в виде закономерности:

, (77)

Здесь слева от знака равенства – кинетическая энергия, а справа – потенциальная энергия. Иными словами, здесь произошло расширение формулы энергии Эйнштейна с точки зрения представления объекта в виде двух противоположностей (корпускулярно-волновой дуализм) с учетом, что волновые процессы однозначно связаны с частотой. И эта формула была экспериментально подтверждена в 1927 году Дэвиссоном и Джермером при исследовании отражения электронов от монокристалла никеля [31, с. 63]. При этом, чтобы оправдать связь массы покоя с частотой, Луи де Бройль постулировал существование волнового поля:

, (78)

Не зная, что собой физически представляет это волновое поле, физики стали интерпретировать его как функцию, которая характеризует вероятность. Но мы отметим, что при эксперименте [31, с. 63] с однозначно получаемой формулой, случайностей нет. И это как раз исключает связь функции Луи де Бройля со случайными процессами, По сути Луи де Бройль утвердил представление объектов мироздания в одной противоположности в виде волновых процессов, а в другой противоположности в виде корпускул с массой покоя. С привлечением нашей теории по связи констант, массы покоя, скорости света и постоянной Планка мы имеем, что известная формула Луи де Бройля [31, с. 63] для движущейся частицы без воздействия внешних сил может быть выведена из аргумента волновой функции (72). Как мы показали выше эта волновая функция (72) вида была использована Дираком для перехода от волновых свойств к корпускулярным свойствам движущейся частицы. В этом случае имеем:

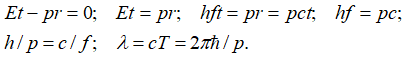, (79)

Однако, надо отметить, что волновая функция (78) соответствует варианту для неподвижной частицы и характеризует связь частоты волнового процесса с массой покоя. Понятно, что нам надо понять каким образом функция Луи де Бройля должна описывать движущуюся частицу. Тут надо отметить, что способ отражения корпускулярно-волновых свойств, исходя из функции Луи де Бройля (78), с соответствующим представлением значения Ψ₀ по геометрии Минковского и учетом формулы (20), может быть представлен в виде:

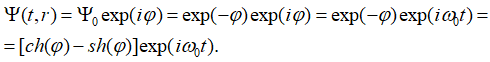, (80)

При таком представлении объект имеет корпускулярно-волновое представление в обеих противоположностях и за счет мнимой единицы происходит смена корпускулярного представления на волновое представление, и наоборот. При сравнении (80) с формулой (20) мы вариант представления по (80) получим, если сделаем перенос функций внутри нижнего равенства в (20) с конечным результатом в виде: . То есть отражение объектов в противоположностях в (20) в чисто волновом или корпускулярном виде, меняется на представление объектов в противоположностях в корпускулярно-волновом виде по (80). Иными словами, в противоположностях присутствуют эквивалентные по виду объекты. Отличие их в том, что волновая часть одного объекта в одной противоположности (системе наблюдения) представляется корпускулярной частью в другой противоположности (системе наблюдения связанной с первой через скорость света). Для второго объекта все, наоборот, так как в противном случае мы бы не имели разницы в представлении в противоположностях. В этом случае учитывается, что время в аргументе при смене системе наблюдения трансформируется в длину. Понятно, что формула (80) выражает существование корпускулярно-волнового объекта в одной из систем наблюдения в качестве частицы в состоянии покоя. Для корпускулярно-волновой частицы, движущейся со скоростью v волновая функция Луи де Бройля представляется в виде:

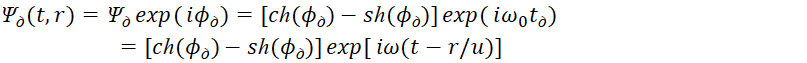, (81)

Где , , . Иными словами, введено изменение параметров длины и времени с пересчетом значений в соответствии с СТО и ОТО Эйнштейна. Следовательно, в этом случае формула Луи де Бройля имеет вид: hf=mc². Так как аргумент функций подчиняется преобразованиям Лоренца-Минковского, а мы показали, что это соответствует замкнутой системе изменений между длиной и временем в виде окружности в [14, с. 5-37], то проблем с бесконечностью не возникает. Парадокс здесь связан еще и с тем, что возникает некая фазовая скорость , которая должна превышать скорость света. Чтобы избежать этих чудес, необходимо было признать существование противоположной системы наблюдения с учетом того, что константы электрической и магнитной проницаемости характеризуют пространственно-временное искривление среды из-за движения противодействия в противоположности, что подробно разъяснено в [19, с. 119]. Собственно, на самом деле эта проблема решена, за счет получения корпускулярных свойств через волновые свойства по системе уравнений Дирака, что как раз и позволяет за счет взаимодействия совместить корпускулярные и волновые свойства в одном объекте. Однако физики, чтобы оправдать движение с фазовой скоростью которая больше, чем скорость света выдвинули гипотезу наличия тахионов [32, с. 291].

Понятно, что обратно пропорциональные величины констант электрической и магнитной проницаемости (противоположности у нас связаны через обратно-пропорциональную связь) характеризуют в пространственно-временном искривлении фазовую скорость u благодаря формуле:

, (82)

Разница лишь в том, что в (81) рассматривается частный случай для одной движущейся частицы, а константы электрической и магнитной проницаемости характеризуют усредненную кинетическую энергию движущихся частиц в противоположности.

Иными словами, Луи де Бройлю для связи волновых процессов с пространственно-временным искривлением оставалось лишь признать сам переход от преобразований Минковского к волновым функциям, и наоборот, полученным в [13, с. 226] с соблюдением закона сохранения количества в аргументах за счет атрибута принадлежности в виде мнимой единицы, что меняет систему наблюдения за счет :

, (83)

Понятно, что Луи де Бройль, (так же как Шредингер и Дирак) не мог связать свои функции с электромагнитными функциями. Это связано с тем, что электромагнитные функции, в соответствии с классическими уравнениями Максвелла, рассматривались как действительные, а не как комплексные функции (не было правила смены функций за счет смены атрибута принадлежности (мнимая единица), что интерпретируется как смена системы наблюдения из одной противоположности на другую). Кроме того, изменения во времени волновой функции по (78) никак не связывались со статикой пространственно-временного искривления, и эту проблему в своей геометрии Минковский решил через равенство [13, с. 226], то есть, как бы привел противоположности в эквивалент одного вида. Фактически Минковский обозначил длину и время как противоположности, связанные через скорость света (скорость обмена), а Фейнман интерпретировал их как плотности зарядов на основании относительности электрических и магнитных полей в зависимости от скорости. Отсюда статика в одной из них будет выглядеть динамикой движения (изменения) в другой в силу того, что время и длина в противоположностях меняются местами. Следующий шаг по связи противоположностей через мнимую единицу интуитивно сделали в квантовой механике [15, с. 317], и это, по сути, означает выполнение закона действия с противодействием, с выполнением разницы между противоположностями, когда сложение в одной противоположности выглядит вычитанием в другой. При этом при соответствующей нормировке это означает общую формулу мироздания как неисчезающей константы через равенство противоположностей в виде 1=i. И это тоже сделано до нас! Таким образом, физики уже сами фактически ввели связь корпускулярных и волновых свойств в виде уравнений Дирака (68) с учетом мнимой единицы, и нам оставалось лишь объяснить это логически и дать физическую интерпретацию.

Понятно, что при описании функций Луи де Бройля как функций связанных с электромагнитными процессами необходимо рассматривать решение последнего уравнения (66), с учетом того, что напряженность электрического поля Е имеет комплексный вид, а Ф=сА. Отсюда имеем:

, (84)

Решение данного уравнения основано на формировании напряженности поля с учетом связи векторных потенциалов с константами электрической и магнитной проницаемости, так как они характеризуют общую энергию движения зарядов в противоположности по аналогии с (43) в виде . Отсюда обобщенный корпускулярно-волновой объект (на основе усредненной кинетической энергии от противоположности) будет характеризоваться в этой системе наблюдения функцией:

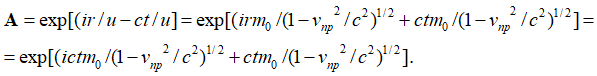, (85)

Однако в системе наблюдения связанной с этой через скорость света происходит смена времени на длину со сменой функции за счет мнимой единицы, которая как раз и характеризует этот переход в виде t=r_пр=iсt_пр. Собственно такой переход исключает замкнутость в пределах одной частицы (а это дает вечный двигатель) и соответствует смене уровня иерархии на величину h=1/c. В результате имеем:

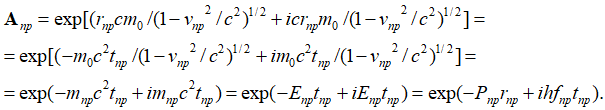, (86)

Этот вид функции соответствует функции Луи де Бройля по (80) и общему уравнению мироздания (20) для неподвижной частицы. Масса покоя, а также и частота такой частицы определяется по формуле .

Соответственно теперь необходимо рассмотреть, как на решение (86) влияет дополнительное движение частицы по формуле (81) в нашей системе наблюдения. Исходя из (81) мы видим, что при движении со скоростью v изменяется параметр времени в соответствии с СТО в виде:

, (87)

Следовательно, вариант с движущейся частицей будет отличаться от варианта с неподвижной частицей (86) за счет приравнивания значений времени с учетом СТО в виде

Как мы показали выше сам принцип перехода к корпускулярным свойствам за счет волновой функции Луи де Бройля Ψ в виде [33, с. 31] представлен в квантовой механике на основе системы уравнений Дирака в дифференциальной форме:

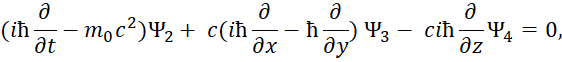
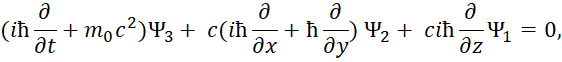
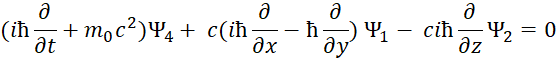, (88)

Представление системы уравнений Дирака (88) в противоположной системе наблюдения получается умножением членов уравнения на мнимую единицу i. В итоге получаем вид:

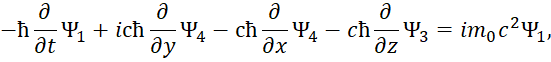
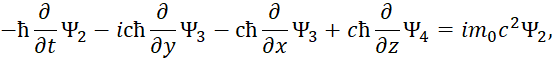
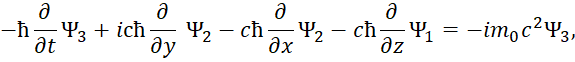
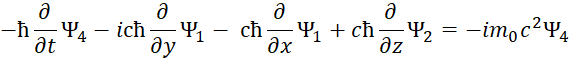, (89)

Такое отображение системы уравнений Дирака при массе покоя равной нулю соответствует виду усовершенствованных уравнений Максвелла. Чтобы получить идентичность нам надо показать необходимость представления волновых функций Ψ для частицы через электромагнитные функции, исходя из логики и практики физических процессов. С этой целью вспомним, что система уравнений Дирака при массе покоя равному нулю m₀=0 в квантовой механике переходит в волновые уравнения нейтрино и антинейтрино, рисунок 1.

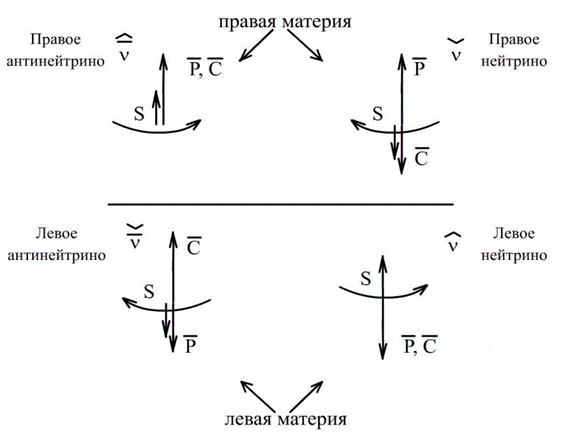
Рис. 1. Нейтрино и антинейтрино

Понятно, что понятие материи не имеет в нашей теории никакого физического обоснования, так как не имеет математического описания с наличием количества, и оно связано с отсутствием понимания учеными происходящих в мироздании процессов. Для описания нейтрино и антинейтрино используется уравнение с двухрядными матрицами Паули (уравнение Вейеля), либо уравнение Дирака, с расщеплением на два независимых уравнения [34, с. 355]:

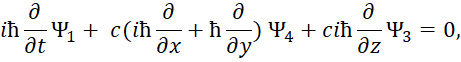
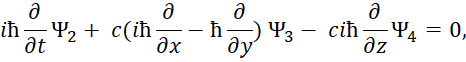
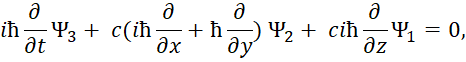
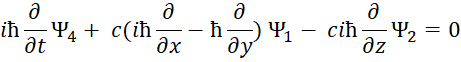, (90)

Так как масса покоя для нейтрино и антинейтрино равна нулю, то отсюда следует вывод об их движении со скоростью света, что соответствует необходимости представления функций Ψ через электромагнитные составляющие, так как с такой скоростью не могут двигаться объекты с иным представлением. О связи функций Ψ с вероятностью также речи быть не может из-за постоянства скорости света. При этом, мы видим, что отличий между первой и второй парой в системе (90) только в обозначении функций. При этом мы не можем оставить прежние обозначения функций, отражающих составные объекты, так как при отсутствии массы покоя происходит преобразование из корпускулярного вида в волновой вид. Это конечно подразумевает иное взаимодействие составных объектов, иначе бы не было изменений. Собственно изменения касаются перехода от корпускулярного представления (потенциальная энергия) в волновое представление (кинетическая энергия), и наоборот. Это по нашей теории в соответствии с общей формулой мироздания (20) интерпретируется через смену закономерностей за счет умножения на мнимую единицу. Именно такой переход от уравнений (88) к уравнениям (89) мы и сделали выше. На основании наших рассуждений с учетом сокращения видов функций Ψ в одном уравнении до двух (Ψ₁ и Ψ₂, или Ψ₃ и Ψ₄), мы можем представить второе и четвертое уравнение в системе (90) в виде:

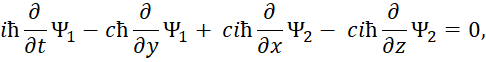
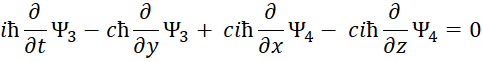, (91)

Сокращение функций до двух (Ψ₁ и Ψ₂, или Ψ₃ и Ψ₄) означает отсутствие связи через массу покоя, а наличие двух функций в уравнении характеризует необходимость наличия в объекте противоположностей. Сократив на постоянную Планка ћ, и умножив на (–i) получим:

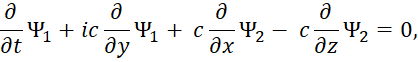
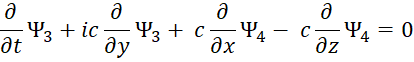, (92)

Иными словами, мы имеем два идентичных уравнения, которые могут только отличаться через функции. Вид уравнений (92) соответствует виду усовершенствованных уравнений Максвелла (28), которые были выведены нами из практического закона Фарадея с учетом закона сохранения количества. Следовательно, если исходить из усовершенствованных уравнений Максвелла (28), то для получения идентичности мы можем выразить функции Ψ следующим образом:

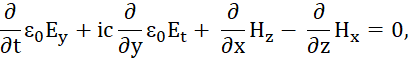
, (93)

Иными словами, мы получаем физические аналоги реализаций функций Ψ₁ и Ψ₂, а также Ψ₃ и Ψ₄, выраженных через реальные электромагнитные составляющие по (28) с учетом констант электрической и магнитной проницаемости, то есть состояния среды. Это означает, что усовершенствованные уравнения Максвелла отражают реальные объекты в виде электронных и мюонных нейтрино и антинейтрино. Собственно, это объясняет эффект аннигиляции электрона и позитрона, которые описываются системой уравнения Дирака с получением фотонов, тем что взаимодействие усовершенствованных уравнений Максвелла дает электромагнитную волну по (63). Это происходит на основе взаимодействия электронных и мюонных нейтрино (антинейтрино). Кроме того, мы имеем физический смысл различий между электронными нейтрино и мюонными нейтрино за счет констант электрической и магнитной проницаемости без выдумывания левой и правой материи. При этом наличие антинейтрино вытекает из комплексно-сопряженного представления по уравнениям (28). По сути, можно считать, что в нейтрино за счет наличия мнимой единицы заложено направление преобразования компоненты напряженности поля от координаты длины в координату времени. Отрицательный знак мнимой единицы в уравнении характеризует антинейтрино и связан с обратным преобразованием координаты времени в координату длины. Отсутствие мнимой единицы не позволяет получить разницу в делении на нейтрино и антинейтрино в силу того, что смена направления наблюдения относительно движущейся частицы меняет и представление о правовинтовом или левовинтовом вращении.

Теперь попробуем показать получение вида корпускулярных частиц не на основе вероятностных волновых функций, а на основе реальных электромагнитных функций, которые в противоположности представляются через векторные потенциалы. Действительно, исходя из (11) с учетом (19) и (42) , мы видим, что разница касается только смены знаков, что можно объяснить сменой системы наблюдения на противоположную систему, из-за перехода от электромагнитных составляющих к векторным потенциалам. Иное бы означало отсутствие отличий как противоположностей.

Исходя из (38) и (41), с учетом равенства , мы на основании суммирования магнитных полей, аналогично тому, как это делается в [28, с. 39] получаем зависимость общей магнитной индукции в виде:

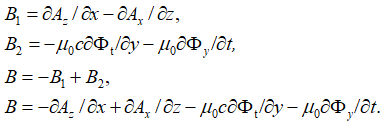
, (94)

Делаем перенос правой части последнего уравнения от знака равенства в левую часть:

, (95)

Аналогично выпишем соответствующее уравнение для электрической индукции из (19) при Н=cE, . При переходе на векторные потенциалы с аналогичным соотношением Ф=сА в силу симметрии законов, происходящих в противоположностях, что связано с законом сохранения количества имеем: . Это аналогично тому, как длина и время меняются местами при переходе в противоположность, и наоборот. Не надо думать, что такая замена, это наша выдумка, подобное симметричное преобразование для движущегося заряда было сделано физиками для магнитной индукции и электрической напряженности поля в [35, с. 29]. Здесь, за счет магнитной индукции на основании константы магнитной проницаемости было учтено состояние среды распространения. В нашем случае это учитывается за счет констант электрической и магнитной проницаемости. При этом мы учитываем симметрию преобразований электромагнитных составляющих и векторных потенциалов с учетом изменения знаков при переходе в противоположность.

На основании суммирования электрических полей, выраженных через векторные потенциалы, аналогично тому, как это делается в [28, с. 39] получаем зависимость общей электрической индукции в виде:

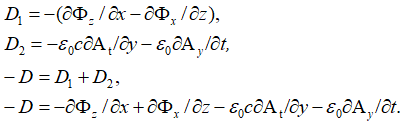, (96)

Соответственно, то, что электрическая и магнитная индукции – это противоположности видно из того, что корпускулярная составляющая, связанная с магнитной индукцией (B), образуется от разности векторных потенциалов, а корпускулярная составляющая, связанная с электрической индукцией (D), образуется от суммы векторных потенциалов. После переноса правой части равенства в левую часть получаем:

, (97)

Таким образом, мы имеем два уравнения с отображением через векторные потенциалы магнитной и электрической индукции в виде:

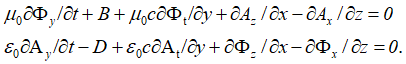, (98)

При нормировке на константы электрической и магнитной проницаемости получим:

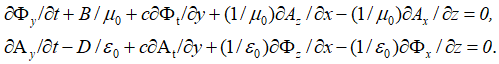, (99)

Иными словами, все наши действия в точности соответствуют тому, что было проделано в классической электродинамике. Далее мы переходим в противоположную систему от электрической и магнитной индукции к векторным потенциалам по принципу замены длины на время в виде r=ict [15, с. 317], предложенному в квантовой механике. Собственно такой переход с изменением на скорость света исключает полную замкнутость корпускулярно-волновых объектов с нахождением в одной противоположности по принципу вечного двигателя, так как при переходе в противоположность меняется уровень иерархии на шаг дискретизации h=1/c. Отсюда , и мы имеем вид:

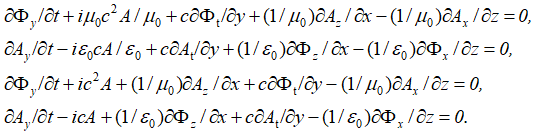, (100)

Кроме того, для того, чтобы привести к единому виду, надо поменять значения А_t на Ф_t, и наоборот. Это можно сделать, если учесть разницу на константы электрической и магнитной проницаемостей в среде по координатам длины, исходя из равенства и , то есть ‒ это связь, которая должна быть в противоположности между подвижным и неподвижным объектом по СТО, по аналогии с (43), где вместо v, значение . Отсюда верны уравнения:

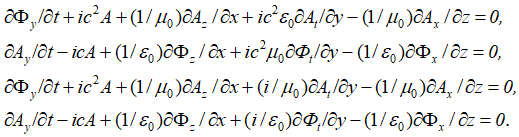, (101)

Повторим, что константы электрической и магнитной проницаемости по нашей теории можно представить в зависимости от некоторой общей переменной u₀ в виде:

, (102)

Отсюда имеем вид:

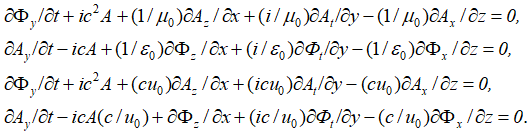, (103)

Учитывая связь между электрическими и магнитными составляющими в виде Ф=сА (это изначальная связь между противоположностями через скорость света без учета СТО) мы можем записать:

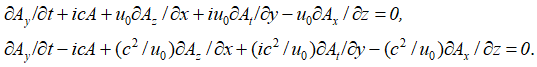, (104)

Сопоставляя систему уравнений Дирака с уравнениями (104), с учетом нашей теории, можно отметить, что m₀c² =c. Кроме того сравнивая уравнения (104) с уравнениями Дирака, мы видим, что мы определили только две составляющие частицы по координатам, в то время как полное определение частицы должно быть по четырем ортогональным координатам пространства и времени. Иначе независимость от системы мироздания в силу отсутствия компонент по пространственно-временным параметрам. Причем вид всех уравнений должен учитывать наличие противоположного представления, которое не приводило бы к идентичности представления. Как это можно сделать на основе смены знаков продемонстрировал Дирак через свою систему уравнений. Кроме того, необходимость смены знаков для противоположностей следует и из общей формулы мироздания (20), и также интуитивно применено физиками при получении суммарных электрических и магнитных полей через векторные потенциалы в [28, с. 39]. Поэтому отразим противоположные изменения аналогично и с учетом нашей теории при m₀c²=c с умножением уравнений на мнимую единицу (i), что означает переход в противоположную систему наблюдения, получим систему уравнений вида:

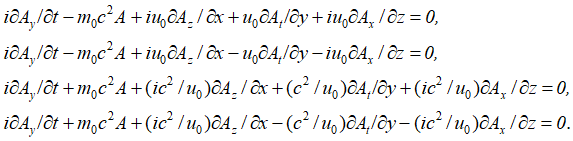, (105)

Собственно умножение на мнимую единицу уравнений требуется в силу того, что в ином случае нет преобразований с условием закона сохранения количества для перехода в корпускулярный вид со сменой функций. Однако понятно, что распределение по координатам векторного потенциала А должно обеспечивать замкнутое взаимодействие по всем четырем координатам для исключения распада частицы в динамике взаимодействия из-за наличия массы покоя.

В этом случае, по аналогии с системой уравнений Дирака, мы получаем, что при начальных функциях А_x,А_y,А_z,А_t мы должны удовлетворить четырем уравнениям которые характеризуют четыре взаимодействующих части объекта по координатам и времени по замкнутому обмену. Соответственно в каждом из уравнений мы имеем отражение динамики взаимодействия частей объекта по четырем координатам таким образом, что это позволяет избежать распада или роста до бесконечности. Влияние частей объекта по координатам длины и времени Дирак выразил через функции вида Ψ₁ и Ψ₂, а также Ψ₃ и Ψ₄. В этом случае значения функций - объектов А_x, А_y, А_z, А_t в системе уравнений Дирака (88) с учетом сравнения с (105) можно представить в виде:

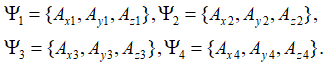, (106)

Фактически мы имеем замкнутое взаимодействие четырех объектов (аналогично замкнутому взаимодействию по координатам длины и величине времени в инвариантной форме) с отражением этих объектов в пространственно-временной среде. Представим эти функции аналогично волновым функциям Шредингера, но без постоянной Планка, согласно формуле (72) в виде Ψ(t,r) =exp(-iЕt+iРr).

В этом случае уравнения (105) распишем по функциям в соответствии с системой Дирака в виде:

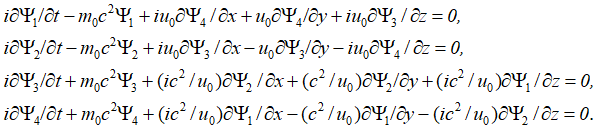, (107)

С учетом операции дифференцирования по Ψ(t,r) =exp(-iЕt+iРr) имеем:

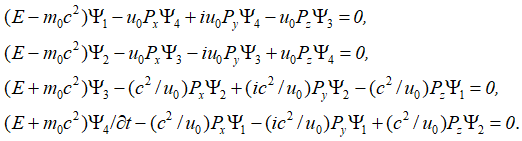, (108)

С учетом выражения одних функций через другие для свободной частицы без внешнего электромагнитного поля получаем:

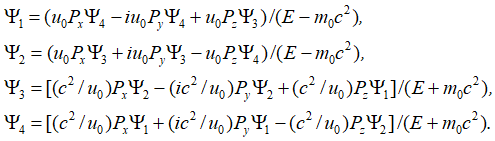, (109)

Далее подставляем одни функции вместо других и сокращаем подобные члены:

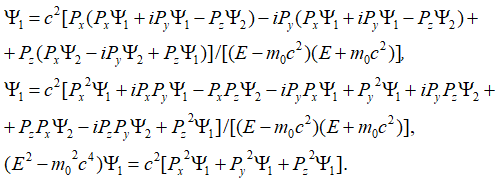, (110)

С учетом сокращения на общую волновую функцию Ψ₁, имеем энергию в квадрате для частиц вида (76). Для отражения движения без наличия внешних сил, как положительных (позитрон), так и отрицательных (электрон) частиц, имеем формулу энергии Эйнштейна:

, (111)

Однако, как известно, электрон и позитрон, как противоположности, аннигилируют с превращением в фотоны. Отсюда их существование было бы невозможно, если бы в соответствии с нашей теорией между глобальными противоположностями не существовало закона, при котором кинетическая энергия в одной противоположности выглядит как потенциальная энергия в другой противоположности. Собственно, мы выше это показали на основе формирования констант электрической и магнитной проницаемости через кинетическую энергию движущихся частиц в противоположности.

В этом случае пространственно-временное искривление неподвижных объектов среды за счет кинетической энергии Е_пр в противоположности определяется значением в аргументе функции волны Луи де Бройля (86) в виде .

Соответственно, учет этого влияния кинетической энергии от противоположности через константы электрической и магнитной проницаемости должен выразиться в изменении значения массы покоя частицы по всем компонентам. Как было отмечено выше для движущейся частицы используется функция Луи де Бройля (81), где влияние среды выражается через изменение времени в соответствии с СТО и ОТО Эйнштейна. Иными словами чтобы учесть влияние среды от кинетической энергии движения в противоположности, мы должны изменить функцию (72) вида Ψ(t,r) =exp(-iЕt+iРr), с учетом пересчета значений времени и длины с поправкой на коэффициент характеризующий кинетическую энергию в противоположности. Причем мы должны учесть, что длина и время в аргументе функции должны иметь связь через скорость света в виде r=ct, так в противном случае не соблюдается условие для получения длины волны Луи де Бройля (79) по уравнению Еt-Рr=0. В этом случае влияние кинетической энергии от движения в противоположности должно применяться ко всему аргументу функции, и мы будем иметь выражение [36, с. 223] при соответствующей системе наблюдения:

, (112)

В этом случае уравнение (107) с учетом операции дифференцирования по Ψ может быть представлено в виде:

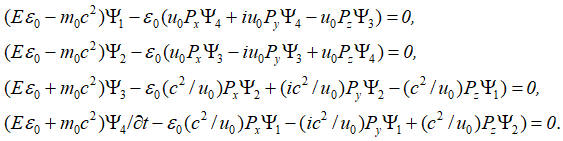, (113)

При нормировке на значение константы электрической проницаемости получаем:

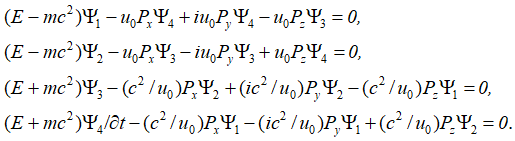, (114)

Надо отметить, что при наблюдении из противоположной системы, когда время меняется на длину, у нас будет не деление на , а умножение. Иными словами, если в варианте (114) масса покоя элементарной частицы представляется по массе наименьшим значением, то в противоположной системе наблюдения она будет наибольшим значением. Это соответствует закону обратно-пропорциональной связи противоположностей по нашей теории мироздания, когда наименьшая величина в одной противоположности является наибольшей в другой противоположности. В противном случае существовали бы одинаковые наименьшие элементарные частицы в обеих противоположностях без иерархии построения и возможности изменения. С учетом выражения одних функций через другие для свободной частицы без внешнего электромагнитного поля получаем:

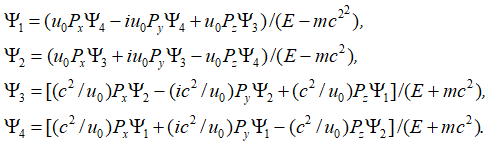, (115)

Далее подставляем одни функции вместо других и сокращаем подобные члены:

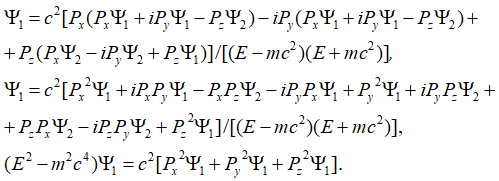, (116)

С учетом сокращения на общую волновую функцию Ψ₁, имеем энергию в квадрате для частиц с учетом кинетической энергии от противоположности. Для отражения движения без наличия внешних сил, как положительных (протон), так и отрицательных (антипротон) частиц, имеем формулу энергии Эйнштейна:

, (117)

Здесь m=1/u₀. Таким образом, мы видим, что масса покоя частиц определяется параметрами через отношения констант электрической и магнитной проницаемости среды (), что в физике интерпретируется как волновое сопротивление среды распространения. Это исключает независимость движущихся частиц от пространственно-временного искривления среды. Собственно, этот вывод ожидаем, так как любой объект взаимодействует с другими объектами через окружающую его среду, и понятно, что без изменений в этой среде не может быть изменений и самого объекта. Иными словами, с учетом кинетической энергии в противоположности мы получаем дополнительную массу для движущейся частицы, например протона (антипротона), положительного или отрицательного пиона. Надо отметить, что без учета влияния среды распространения в виде констант электрической и магнитной проницаемости, данный вывод о необходимости разницы масс между протоном (положительным пионом) и электроном на основе уравнений Дирака никак не мог быть получен. Именно это привело к ошибке представления протона, как объекта, состоящего из кварков и глюонов. Заметим, что для неподвижных объектов среды распространения (Р_r=0), исходя из системы наблюдения от противоположностей (времени или длины), мы будем иметь функции для сторонних зарядов по аналогии с (34) в виде:

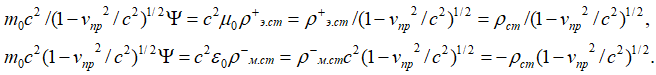, (118)

И как это показано выше, в этом случае объекты среды выражаются в виде своего влияния на реальные движущиеся объекты через магнитную силу и электрическую силу (37).

Собственно сделанное нами предположение о формировании дополнительной массы через взаимодействие электронных и мюонных нейтрино (антинейтрино) подтверждается и распадом дополнительной массы частиц в виде [37, с. 277]:

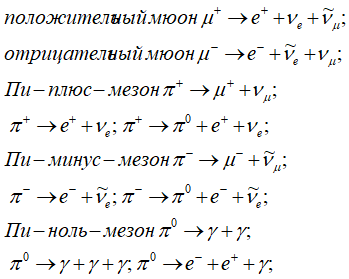, (119)

Здесь е⁺ – позитрон, е^- – электрон, ‒ электронное нейтрино и антинейтрино, ‒ мюонное нейтрино и антинейтрино соответственно. При аннигиляции положительного пиона и отрицательного пиона, или при распаде пи-ноль-мезона, высвобождается кинетическая энергия в виде фотонов (). Из уравнений (119) и по приведенным выше формулам взаимодействия формирования электромагнитной волны, на основе усовершенствованных уравнений Максвелла, следует вывод, что формирование фотонов (электромагнитных волн) происходит на основании взаимодействия либо пары электронных и мюонных нейтрино, либо пары электронных и мюонных антинейтрино. Как видно из уравнений (119) распад связан с тем, что пары электронных нейтрино и мюонных антинейтрино, а также пары электронных антинейтрино и мюонных нейтрино являются независимыми. Действительно, в противоположности распад отрицательного мюона можно интерпретировать как распад нейтрона на протон, электрон и антинейтрино. Причём с учётом перехода волновых свойств в корпускулярные свойства электрон в противоположности может характеризоваться как электронное антинейтрино, а электронное антинейтрино при рассмотрении из противоположности это уже электрон. То есть происходит смена представления. Соответственно мюонное нейтрино в противоположности характеризуется как протон. Преобразование электрона и позитрона происходит только при их взаимодействии через аннигиляцию с превращением в фотоны. Здесь надо учитывать, что электрон и позитрон в соответствии с нашим описанием системы Дирака через электромагнитные составляющие имеют такой их набор, который позволяет при их аннигиляции получить взаимодействие из пар электронных и мюонных нейтрино, а также пар электронных и мюонных антинейтрино. Иными словами, дифференциальные компоненты в системе уравнений Дирака для электрона и позитрона меняют порядок взаимодействия, и получаются усовершенствованные уравнения Максвелла, соответствующие электронным и мюонным нейтрино (антинейтрино), что дает уже взаимодействие, соответствующее электромагнитным волнам (это мы показали выше). Понятно, что физиков также удивляет отсутствие распада протона по сравнению с положительным пионом. Чтобы это обосновать придумали некий барионный заряд, а протон стали представлять состоящим из неких кварков и глюонов. Однако наша теория решает этот парадокс, и отсутствие распада протона связывает с устойчивостью в динамике взаимодействия и обмена, которое наступает на максимуме излучения по формуле Планка с учетом соответствующего коэффициента 4.965 [38, с. 31]. Тогда с учетом констант магнитной и электрической проницаемости имеем массу протона в нормированном количественном виде:

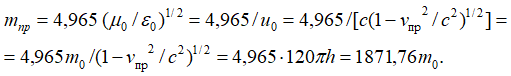, (120)

Здесь мы учитываем, что значение , получаемое в системе измерения СИ, не соответствует системе измерения мироздания и дает парадокс, связанный с тем, что отношение констант магнитной и электрической проницаемости соответствует числу. Это возможно только в том случае, если их разница определяется только количественными коэффициентами при произведении . По нашей теории . А это означает, что при отношении значений констант магнитной и электрической проницаемости помимо количественной разницы в системе измерения мироздания будет еще разница на значение в скорость света. Иначе отличий нет, и константы электрической и магнитной проницаемости не будут являться противоположностями. Соответственно, вместо значения в системе измерения СИ, в нашем случае должна стоять величина . Отметим, что практическое вычисленное значение массы протона относительно массы электрона равно 1836 и расхождение связано с тем, что мы учитывали условие термодинамического равновесия для идеального случая при существовании только водородоподобного атома. В реальности обеспечить такие условия невозможно.

Понятно, что использование функции вида (72) в уравнении Дирака для описания движения частицы с постоянной скоростью означает замкнутость процессов в пределах одной частицы без взаимодействия. Это аналогично варианту рассмотрения движения электромагнитной волны без вторичных источников по принципу Гюйгенса-Френеля. Именно поэтому мы для уравнений волн вида (51) использовали решения в виде функций (53). Отсюда следует вывод, что для описания реальных процессов необходимо на основании волновой функции характеризовать взаимодействие частиц. Но при взаимодействии присутствуют силы и в этом случае изменение движения частиц основано на использовании начального уравнения Ньютона F=ma c переходом к уравнению Гамильтона-Якоби с наличием внешнего поля для взаимодействия. Чтобы показать это силовое взаимодействие Дираком в аргумент функции был добавлен член . В итоге была получена функция вида . Соответственно в уравнения было добавлено и внешнее электрическое поле. Отсюда система уравнений Дирака с учетом воздействия внешних сил переходит в уравнения Паули [39, с. 310] (это общий случай из двух уравнений Шредингера). То есть, ввод данного члена в аргумент функций соответствует динамике взаимодействия противоположностей, что без воздействия сил невозможно. Этот вопрос более детально мы разберем в следующих публикациях.

Таким образом, мы видим, что применение усовершенствованных уравнений Максвелла не явилось самоцелью и позволило:

1. Связать усовершенствованные уравнения Максвелла с реальными объектами в виде электронных и мюонных нейтрино (антинейтрино).
2. Показать переход к волновым электромагнитным уравнениям с источниками, как излучения, так и поглощения на основе того, что объекты среды распространения, характеризуются константами электрической и магнитной проницаемости.
3. Обосновать комплексное представление электромагнитных функций для описания корпускулярно-волнового дуализма с учетом общей формулы мироздания (20) на основе нашей теории, где введение мнимой единицы в усовершенствованные уравнения Максвелла позволило обеспечить переход от волновых свойств к корпускулярным свойствам через систему уравнений Дирака и тем самым доказать электромагнитное происхождение массы.
4. Показать, что формула Луи де Бройля при массе покоя соответствует формированию электромагнитного излучения и поглощения объектами среды распространения с учетом кинетической энергии в противоположности (86). При этом длина волны Луи де Бройля в соответствии с нашей теорией выводится из уравнения Et-Pr=0, что соответствует свободному движению частицы без внешних сил.
5. Выявить переход от усовершенствованных уравнений Максвелла к представлению объектов в корпускулярном виде, при наличии разницы массы в противоположных системах наблюдения. Это противоречит принятой концепции в электродинамике о необходимости наличия неких сдерживающих сил с отказом от электромагнитного формирования частиц [40, с. 271]. При этом введение в уравнения Максвелла значений реальных токов и зарядов не является корректным, так как движение заряженных частиц следует из взаимодействия электронных и мюонных нейтрино (антинейтрино) на основе усовершенствованных уравнений Максвелла в соответствии с системой уравнений Дирака. Соответственно изменения, связанные с излучениями и поглощениями, выражаются в изменении параметров в этой системе уравнений.

Понятно, что иного варианта описания процессов предложить невозможно, так как вопрос касался лишь замены вероятностных волновых функций на реальные электромагнитные функции. Поэтому нас очень удивил ответ из Администрации Президента РФ, по которому нам отказано даже в обсуждении (ответ приведен на рисунке 2).

Рис. 2. Ответ из Администрации Президента РФ

Иными словами, физики отрицают уже то, что получено давно на практике, так как мы просто связали в логическую цепочку то, что уже использовалось на практике, и было получено до нас. Можно было бы отвергать нашу теорию, но тогда надо иметь альтернативную теорию без чудес типа телепортаций, кварков, глюонов, темной энергии и материи, виртуальных частиц, гравитонов, черных дыр, орбиталей, электромагнитных и электронно-позитронных вакуумов, барионных зарядов, ядерных сил и прочих ложных утверждений. Однако иных подходов без чудес у «корифеев» науки нет, а есть лишь математические подгонки под результат. Отсюда тогда вопрос: «Что заставляет физиков отвергать то, что уже фактически давно введено в практику и теорию, и требовалось лишь правильно все логически связать и обосновать?» Мы можем дать этому объяснение только через преследование ими корыстных целей!