1. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
По закону всемирного тяготения [1], сила взаимного притяжения тел находится по формуле:
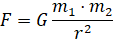, (1.1)
G=6,67·10-11 Н·м2/кг2 – универсальная гравитационная постоянная; m1, m2 – массы тел, r – расстояние между телами. Из формулы (1.1) следует, что первое тело имеет ускорение:
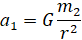. (1.2)
Создается [2] функция пользователя ЗВТ, возвращающая значение переменной, входящей в формулу (1.1), когда заданы значения двух других переменных. Код функции ЗВТ и ее описания:
Function ЗВТ(Сила_Н, Масса1_кг, Масса2_кг, _
Расст_м, F_M_R As String)
Select case F_M_R
Case ”F”
ЗВТ = 6.67 * 10 ^ (-11) * Масса1_кг * Масса2_кг/ _
Расст_м ^ 2
Case ”M”
ЗВТ = Сила_Н* Расст_м ^ 2/6.67 / 10 ^ (-11)/ Масса1_кг
Case ”R”
ЗВТ = (6.67 * 10 ^ (-11) * Масса1_кг * Масса2_кг/ _ Сила_Н)^(1/2)
End Select
End Function
Sub InstallFunc1()
Application.MacroOptions Macro:=”ЗВТ”, _
Description:= ”При F находит величину силы тяготения, ” & _
”при М – массы2, при R - расстояния”
End Sub
Задача 1.1. Два астероида массами 20 т и 30 т приблизились к друг другу на расстояние 250 м. Какова сила их взаимного гравитационного притяжения?
Технология решения. Вызывается функция ЗВТ, вводятся числовые данные и ”F”, что ниже возвращает результат (рис. 1).
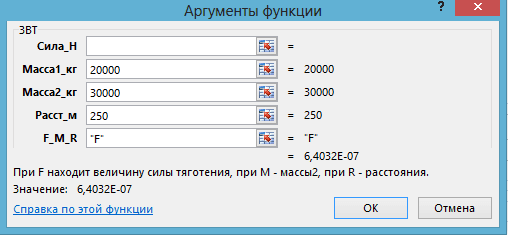
Рис. 1. Применение функции ЗВТ в задаче 1.1
Задача 1.2. Искусственный спутник Земли массой 85 кг движется по круговой орбите на расстоянии 6600 км от центра Земли. Какое ускорение имеет спутник благодаря силе гравитации?
Технология решения. Вызывается функция ЗВТ и вводятся данные (рис. 2).
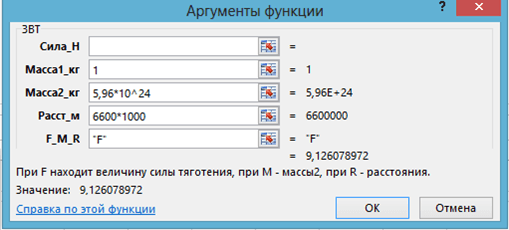
Рис. 2. Применение функции ЗВТ в задаче 1.2
Задача 1.3. На каком расстоянии от центра Земли ускорение свободного падения равно 3 м/с2?
Технология решения. Вызывается функция ЗВТ, вводятся числовые данные и ”R” (рис. 3).
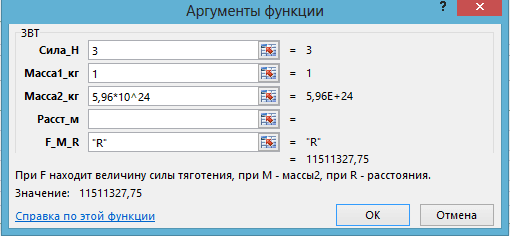
Рис. 3. Применение функции ЗВТ в задаче 1.3
2. РАВНОМЕРНОЕ ВРАЩЕНИЕ
При движении материальной точки с постоянной скоростью v по окружности радиуса R ее ускорение, называемое центростремительным, находится [1] по формуле:
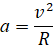. (2.1)
В силу формулы (2.1), величина силы, под действием которой происходит вращение, определяется формулой:
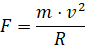. (2.2)
В частности, если F является силой притяжения тел массами m и M, то должно выполняться:
.
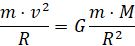Поэтому справедливы формулы:
, 
, 
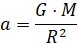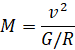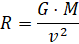. (2.3)
Создается функция пользователя ВРАЩЕНИЕ, возвращающая значение переменной формулы (2.1), когда заданы значения двух других переменных.
Код функции ВРАЩЕНИЕ и ее описания:
Function ВРАЩЕНИЕ(Ускор_м_с2, Скор_м_с, Радиус_м, _
A_V_R As String)
Select case A_V_R
Case “A”
ВРАЩЕНИЕ = Скор_м_с ^ 2 / Радиус_м
Case “V”
ВРАЩЕНИЕ = (Ускор_м_с2 * Радиус_м) ^ (1/2)
Case “R”
ВРАЩЕНИЕ = Скор_м_с ^ 2 / Ускор_м_с2
End Select
End Function
Sub InstallFunc2()
Application.MacroOptions Macro:=”ВРАЩЕНИЕ”, Description:= _
”Возвращает при A величину ускорения, ” & _
”при V – скорости, при R - радиуса”
End Sub
Задача 2.1. При работе стиральной машины поверхность ее барабана, находящаяся на расстоянии 21 см от оси вращения, движется вокруг этой оси со скоростью 15 м/с. Определите ускорение, с которым движутся точки поверхности барабана.
Технология решения. Вызывается функция ВРАЩЕНИЕ, вводятся данные задачи и “A”, ниже появляется результат (рис. 4).
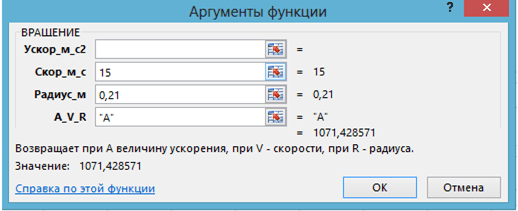
Рис. 4. Применение функции ВРАЩЕНИЕ в задаче 2.1
Задача 2.2. Применяя функцию ВРАЩЕНИЕ, найдите 1-ю космическую скорость.
Технология решения. Вызывается функция ВРАЩЕНИЕ, вводятся числовые данные и “V” (рис. 5).
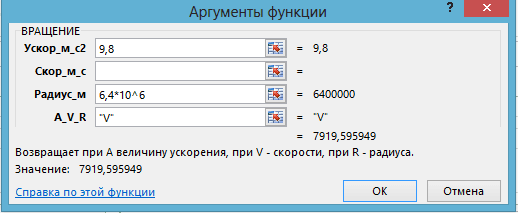
Рис. 5. Применение функции ВРАЩЕНИЕ в задаче 2.2
3. ЗАКОН СОХРАНЕНИЯ ПОЛНОЙ ЭНЕРГИИ
Полная механическая энергия E материального тела находится по формуле:
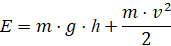. (3.1)
По закону сохранения полной механической энергии, в консервативной системе величина Е в течении времени не изменяется: ΔЕ = 0.
Создается функция пользователя ЗСПЭ, возвращающая значение переменной формулы (3.1), когда заданы значения всех других переменных. Код функции ЗСПЭ и ее описания:
Function ЗСПЭ(Энергия_Дж, Масса_кг, Высота_м, _
Скорость_м_с, E_M_H_V As String)
Select case E_M_H_V
Case “E”
ЗСПЭ = 9.8 * Масса_кг * Высота_м + Масса_кг * _
Скорость_м_с ^ 2 / 2
Case “M”
ЗСПЭ = Энергия_Дж /(9.8 * Высота_м + Скорость_м_с ^ 2 / 2)
Case “H”
ЗСПЭ = (Энергия_Дж - Масса_кг * Скорость_м_с ^ 2 / 2)/ _
(9.8 * Масса_кг)
Case “V”
ЗСПЭ = (2*( Энергия_Дж -9.8 * Масса_кг * Высота_м)/ _ Масса_кг)^(1/2)
End Select
ЗСПЭ=Round(ЗСПЭ,4)
End Function
Sub InstallFunc3()
Application.MacroOptions Macro:=”ЗСПЭ”, Description:= _
”Возвращает при Е величину полной энергии, ” & _
”при M – массы, при H – высоты, при V - скорости ”
End Sub
Задача 3.1. Тело массой 200 г падает с высоты 4 м. Применяя функцию ЗСПЭ, найдите скорость, которую оно будет иметь на высоте 1 м от земли.
Технология решения. 1. Вызывается функция ЗСПЭ и находится величина полной энергии в начальный момент времени:
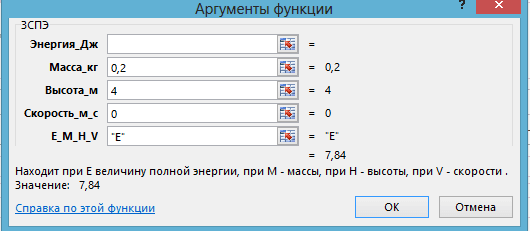
Рис. 6. 1-е применение функции ЗСПЭ в задаче 3.1
2. Снова вызывается функция ЗСПЭ и находится скорость на высоте 1 м:
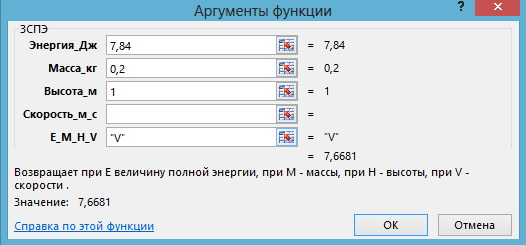
Рис. 7. 2-е применение функции ЗСПЭ в задаче 3.1
.png&w=640&q=75)
