Развитие электродинамики и физики на основе теории мироздания. Часть 2. Подгонки под результат в квантовой механике и физике. Часть 7

В публикации [1, с. 5-36] было приведено доказательство, как система уравнений Дирака выводится из усовершенствованных уравнений Максвелла (электронные и мюонные нейтрино и антинейтрино). В силу того, что волновые функции, характеризующие вероятность, меняются на электромагнитные волновые функции, а сами уравнения образуют замкнутую систему при преобразовании, следует вывод об электромагнитном происхождении корпускулярных свойств, а значит и массы частиц. Иными словами, мы фактически доказали идею Дж. Дж. Томсона об электромагнитном происхождении массы электрона, которая была отвергнута физиками из-за того, что они считали, что требуются некие сдерживающие силы [2, с. 271] для исключения отталкивания зарядов. Ошибка физиков была в том, что они предполагали заряды как нечто дробное и отдельное содержащееся в пространстве и времени на основе ими же придуманных систем измерения (это же касалось и массы). Отсюда в 1964 г. Гелл-Манн выдвинул гипотезу, согласно которой все элементарные частицы построены из трёх частиц, названных кварками. Этим частицам приписываются дробные квантовые числа, в частности электрический заряд, равный +2/3, +1/3, ‒1/3 соответственно для каждого из трёх кварков [3, с. 296]. При этом магнитный спин должен быть равен для всех трёх кварков ½. То есть физики разделили в кварках электрические и магнитные силы и тем самым опровергли необходимую связь электрических и магнитных сил, а значит и уравнений Максвелла!

Таким образом, физики не приняли во внимание факт, что переход от волновых свойств к корпускулярным свойствам по уравнениям Дирака уже давал однозначную связь электромагнитных свойств с корпускулярными свойствами в силу того, что сама система уравнений обеспечивает замкнутый вид преобразований. Кроме того, заряды по Фейнману из-за необходимости электромагнитного континуума (однозначное преобразование электрических сил в магнитные, и наоборот) уже были связаны с пространственно-временным искривлением [4, с. 273]. Иными словами, если исходить из подчинения плотности зарядов преобразованиям Лоренца-Минковского, то, более мелких положительных или отрицательных зарядов, которые бы расталкивались, просто быть не может. Действительно, сжатие или растяжение уже связано с преобразованиями Лоренца-Минковского с учётом представления зарядов в виде объектов среды распространения через длину и время. Соответственно, никаких иных сдерживающих сил, которые бы влияли на это сжатие или растяжение, здесь не предусматривается. Их просто нет в преобразованиях Лоренца-Минковского, которые выводятся из замкнутого взаимодействия по окружности двух глобальных противоположностей, и ничего иного вставить в эти преобразования невозможно. Третья величина в замкнутую систему двух противоположностей не вписывается! В публикации [5, с. 5-37], мы доказали, что количество объектов среды распространения ограничено в силу необходимости наличия константы в скорость света и постоянной Планка в виде N=c/h (скорость света и постоянная Планка в системе Мироздания ‒ это не величины в системах СИ или СГС). Собственно, это подтверждалось отсутствием ультрафиолетовой катастрофы (рост энергии до бесконечности) за счёт ограничения в величину постоянной Планка, и тем, что без наличия скорости света как константы не выполнялись бы законы физики в разных системах отсчёта. Моментальное противодействие на действие из-за бесконечной скорости не даёт возможности для изменений, а значит и законов физики. Ограничение же количества объектов следовало из необходимости связи всех объектов мироздания через обмен со скоростью света. В противном случае были бы объекты вне взаимодействия. Нечто подобное в виде постоянной тонкой структуры были вынуждены ввести и физики в квантовой механике в виде . Разница с нашим подходом в нормировке, которая в интерпретации физиков не соответствует охвату всех объектов Мироздания при взаимодействии со скоростью света. При этом из СТО и ОТО Эйнштейна следует наличие двух равноправных глобальных противоположностей, характеризуемых длиной и временем, которые связанны через скорость света. При этом, при наблюдении от каждой глобальной противоположности, кинетическая энергия в одной противоположности переходит в потенциальную энергию в другой противоположности, в противном случае различий нет. По этой же причине, соответственно объекты длины и времени при наблюдении от каждой из глобальных противоположностей также меняют свой вид и естественно их отличие связано с разным представлением по СТО и ОТО Эйнштейна. Для взаимодействия объекты длины и времени должны изменяться через обмен с условием закона сохранения количества, иное приводило бы к исключению одной из противоположностей. Данный обмен связан с преобразованием кинетической энергии в потенциальную энергию, и наоборот. Наличие кинетической энергии связано с движением объекта среды распространения в одной из глобальных противоположностей, так как иначе зафиксировать наличие кинетической энергии невозможно. Соответственно в противоположности эта кинетическая энергия рассматривается как потенциальная энергия в виде массы. Такое различие – это корпускулярно-волновой дуализм из глобальных противоположностей, так как разница масс объектов длины и времени даёт и отличие противоположностей в представлении объектов. Действительно, характеристика объектов Мироздания только через разницу в скорость света не даёт динамики изменений самих объектов, они являются константами с однородным представлением. Практически все необходимые предпосылки для восприятия зарядов и массы покоя в виде объектов длины и времени в одной противоположности и в электромагнитном исполнении в другой противоположности уже были введены в физику, оставалось только связать уравнения через соответствующую логику. Однако, данный вариант электромагнитного происхождения массы и корпускулярных свойств был получен нами на основании уравнения энергии Эйнштейна при движении частицы без воздействия внешних сил [1, с. 5-36]. В реальности всегда присутствует взаимодействие объектов Мироздания с влиянием друг на друга за счёт силовых воздействий. Это взаимодействие осуществляется через обмен с формированием изменения значения кинетической энергии частицы. При этом это изменение не может происходить без противодействия в замкнутой системе обмена, что связано с сохранением самой частицы. В противном случае мы бы имели чудеса возникновения из ничего. Соответственно не соблюдалось бы общее уравнение энергии Эйнштейна для двух взаимодействующих частиц при замкнутом цикле. Собственно, как показано в [1, с. 5-36] система уравнений Дирака даёт переход через волновые функции Ψ к корпускулярным свойствам с получением энергии в квадрате в виде:

, (1)

Как мы показали в [5, с. 5-37], здесь также получается замкнутый вид характерный для окружности, а это означает замкнутое взаимодействие противоположностей. Действительно, взятие квадратного корня из уравнения (1) при сокращении волновой функции Ψ даёт неоднозначные решения в виде противоположностей:

, (2)

На этом основании Дирак и предложил свою теорию электронно-позитронного вакуума, причём заряды не имели различие по величие, так как не входили в формулу (2). Их отличие интерпретировалось только знаком в виде положительной и отрицательной энергии [6, с. 349]. При установлении связи между электрическим и магнитным полем Фейнман в [4, с. 273] фактически интерпретировал различие противоположных зарядов по принадлежности к объектам длины и времени. Иными словами, мы не имеем представление о зарядах как о нечто таком вне пространства и времени. В этом случае мы получаем необходимость симметрии в движении противоположных частиц с противодействием друг другу для соблюдения закона сохранения количества в замкнутой системе.

Исходя из нашей теории, взаимодействие противоположностей осуществляется по замкнутому циклу из-за условия необходимости сохранения равного количества между противоположностями. Причём взаимодействие по замкнутому циклу осуществляется через обмен с излучением и поглощением. Процесс излучения по замкнутому циклу физики стали описывать через математическую модель гармонического осциллятора в виде [7, с. 58-59]:

, (3)

Так как движение осуществляется по кругу с равенством изменения составляющих по энергии, то можно записать при n=1:

, (4)

Собственно, это соответствует тому, что получил Бор для момента импульса в [7, с. 58-59]. Так как рассматривается движение по окружности радиусом r₀ со скоростью v, то это даёт излучение электромагнитной энергии. Отсюда, чтобы движение не прекращалось необходимо поглощение энергии. В противном случае приходим к парадоксу падения электрона на ядро. Чтобы избежать этого парадокса, и не сумев понять каким образом осуществляется восполнение энергии, Бор придумал свой постулат отсутствия излучения электроном при движении по дискретной орбите вокруг протона с ускорением [8, с. 55]. Однако каким образом, и за счёт чего при этом будет происходить излучение или поглощение при переходе с орбиты на орбиту, он не объяснил. Обнаружить замкнутую систему без взаимодействия через излучение и поглощение невозможно, такой объект просто отсутствует в Мироздании. Одновременно нам известна формула для энергии:

, (5)

Отсюда мы видим, что есть энергетическое соответствие, которое не противоречит практике в виде:

, (6)

Иными словами, начальная энергия и импульс выступают как противоположности аналогично длине и времени из-за связи через скорость света. Одновременно, исходя из последнего уравнения в (6) следует, что скорость движения по окружности и длина окружности имеют обратно-пропорциональную связь. Это означает, что скорость движения в одной противоположности определяет длину в другой противоположности с учётом нашей теории. Иными словами, динамика движения в одной противоположности даёт статику в другой противоположности. Именно замену скорости, как противоположности к длине, использовал Бор в своём уравнении движения электрона вокруг протона [7, с. 58-59]. Тем самым он фактически признал наличие противоположностей с их обратно-пропорциональной связью. Исходя из системы уравнений Дирака с учётом представления волновых функций Ψ через электромагнитные волновые функции, можно интерпретировать изменение состояния частиц по энергии и направлению движения через импульсы. Собственно, это видно из преобразования формулы (2) в вид:

, (7)

При этом имеем:

, (8)

Для случая замкнутого движения при динамике обмена, аналогичного замкнутости двух глобальных противоположностей друг на друга, когда кинетическая энергия полностью переходит в потенциальную энергию, мы должны считать Е=0,так как иначе, при наличии значения энергии Е не равного нулю, надо предположить третий вид энергии без замкнутого преобразования. Действительно смена направления по замкнутому кругу означает, что любое направление, с течением времени связанное с импульсом, а значит и кинетической энергией, переходит в излучение, которое в противоположности интерпретируется потенциальной энергией. Добавочное значение энергии Е не вписывается в замкнутое движение с переходом в излучение. Отсюда мы можем записать:

, (9)

Это фактически соответствует представлению аргумента волновой функции Луи де Бройля в виде Ψ=exp[i(E_пр r/c‒Pr)]=exp[i(E_пр t‒Pr)]. Иными словами, приходим к соотношению, которое соответствует переходу кинетической энергии движения в потенциальную энергию массы. Здесь значение массы m связывается с наличием кинетической энергии (движения объектов) в противоположности, в противном случае эта масса равняется массе электрона (позитрона) (h=1/c=m₀), то есть начальному параметру объекта среды распространения.

Повторим, что движение по замкнутому кругу частицы не обходится без изменения направления движения, что связано с излучением и поглощением энергии. Это означает смену коэффициентов при параметрах длины в аргументах электромагнитных функций (волновых функций Ψ), что эквивалентно излучению одних электромагнитных составляющих и поглощению других составляющих. Так как взаимодействие осуществляется через среду распространения, то изменение состояния значений импульсов и энергии необходимо характеризовать через силовое воздействие в каждой точке пространства. Это силовое воздействие, как мы показали в [1, с. 5-36] выражается через значения силы Кулона (электрическая сила) и силу Лоренца (магнитная сила). При этом никаких иных сил не предусматривается в силу того, что эти силы подчиняются преобразованиям Лоренца-Минковского с замкнутостью преобразования друг в друга. Воздействие сил описывается через известное уравнение Гамильтона-Якоби, которое при наличии силы F можно рассматривать как прямое следствие известного закона Ньютона:

F=ma=md²s/dt²= mdv/dt;

E=∫Fds=∫Fvdt=∫mvdv=mv²/2=p²/(2m), (10)

Далее по классической физике берётся некая функция действия  с учётом равенств и . В результате имеем уравнение Гамильтона-Якоби без внешнего поля:

, (11)

То есть, в уравнении Гамильтона-Якоби, а также в уравнении Шрёдингера и Паули, присутствует коэффициент пропорциональности, равный 2 ‒ между энергией и импульсом, что говорит об отсутствии полной замкнутости частицы. Действительно, наличие силы, воздействующей на частицу, подразумевает либо получение энергии извне, либо торможение с излучением.

В уравнении энергии Эйнштейна, из которого получается система уравнений Дирака, этого коэффициента нет. Поэтому перейти напрямую от уравнения энергии Эйнштейна к уравнению Гамильтона-Якоби не представляется возможным, и все попытки будут иметь парадоксы. Это связано с тем, что в уравнении энергии Эйнштейна все количественные соотношения приведены как бы к одной общей системе наблюдения с соблюдением замкнутой системы в виде уравнения окружности и наличием инвариантной формы во всех системах отсчёта. В случае воздействия внешней силы такой инвариантности через формулу Ньютона (1) нет. Понятно, что в этом случае уравнению Гамильтона-Якоби должно соответствовать своя система уравнений взаимодействия и функций отличная от системы уравнений Дирака для свободной частицы.

Однако, каким образом система уравнений Дирака должна переходить в корпускулярное движение частицы под действием внешних сил и иметь представление в виде уравнения Гамильтона-Якоби с наличием внешних электрических и магнитных сил?

Данную задачу с переходом от системы уравнений, характеризующих свободное движение частицы на основе формулы энергии Эйнштейна, попытался решить Дирак. С этой целью он интуитивно использовал изменение начальной волновой функции вида , на волновую функцию вида:

, (12)

Иными словами, физики из общей энергии частицы выделили собственную энергию частицы, которая равна [9, с. 292]. Понятно, что данное изменение волновой функции у Дирака не имело объяснение, так как выделение собственной энергии частицы означало бы вычитание, то есть мы бы имели функцию , а не функцию (12). Сложение в (12), как и вычитание, находит объяснение только с точки зрения нашей теории, что будет показано несколько ниже на основе внешнего воздействия с учётом противоположностей. Однако, сейчас важен сам факт того, что при учёте действия внешних сил необходимо аргументы волновых функций в системе уравнений Дирака представлять соответствующим образом.

Это связано с тем, что внешнее силовое воздействие, которое не является инвариантным, исключает симметрию представления волновых функций по аргументам, что связано с противодействием на внешнее действие с достижением необходимого равенства при соответствующем движении частицы. Кроме того, Дирак в свою систему уравнений ввёл электрические и магнитные силы в виде членов векторных потенциалов еФ и е/сА.

Далее посмотрим, каким образом Дираку удалось перейти к системе уравнений Паули, которая при волновом виде замещает уравнение Гамильтона-Якоби как бы через систему уравнений Шредингера. При этом он как бы объяснил наличие магнитного спина. С этой целью повторим всю последовательную логическую цепочку вывода системы уравнений Дирака из уравнения энергии Эйнштейна, так как это поможет нам выявить ошибки, допущенные физиками при наличии воздействия внешних сил на частицу. Первоначальное уравнение энергии Эйнштейна с учётом «линеаризации» имеет вид [10, с. 298]:

(13)

Здесь k изменяется от 0 до 3; P₀=M₀c; P₁=P_x ; P₂=P_y ; P₃=P_z . Из этой записи при использовании матриц для разложения (13):

Следуют известные уравнения, которые дают систему уравнений Дирака. При этом система уравнений имеет вид:

;

;

;

, (15)

Далее конкретные числовые значения заменяются дифференциальными операторами в виде:

, (16)

Которые должны воздействовать на волновую функцию Ψ, и которая, в свою очередь, характеризует вероятность.

Понятно, что при «линеаризации» Дирак не опирался на реальные физические процессы для получения уравнения энергии Эйнштейна вида (13) и использовал функции, которые характеризуют вероятность вида:

, (17)

Собственно такой вид соответствует функции Луи де Бройля для объектов Мироздания в отдельном замкнутом виде. Так постоянная Планка ћ присутствует при дифференцировании во всех членах, то её можно исключить из дальнейшего рассмотрения. Соответственно имеем вид функций при движении частицы без наличия внешних сил:

, (18)

При выражении одних функций через другие, с учётом дифференцирования для свободной частицы без внешнего электромагнитного поля, получаем:

, (19)

Далее выражаем одни функции через другие:

, (20)

На следующем этапе подставляем одни функции вместо других и сокращаем подобные члены:

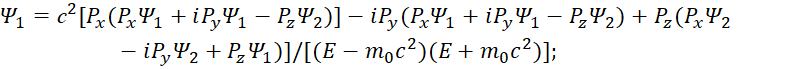
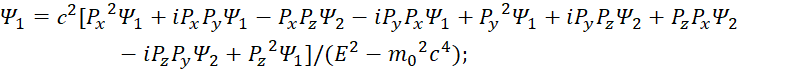
, (21)

Сокращая на волновую вероятностную функцию, получаем уравнение энергии Эйнштейна в квадрате для взаимодействующих противоположных частиц:

, (22)

Аналогичный результат мы имеем и для других волновых функций.

Таким образом, Дирак интуитивно показал, как можно перейти от уравнений волны в комплексном виде к отображению свойств корпускулярных частиц. Иными словами, Дирак без всяких неких сдерживающих сил для зарядов получил однозначный переход от волновых свойств, характеризующих вероятность, к корпускулярным свойствам. Мы лишь только придали этим волновым функциям реальный физический смысл, заменив их в [1, с. 5-36] на реальные электромагнитные функции. Однако для случая воздействия на частицу внешних сил операторы (16) были расширены с учётом этих самых внешних сил в виде:

, (23)

Отсюда систему уравнений Дирака мы можем записать в виде матричного уравнения [11, с. 310]:

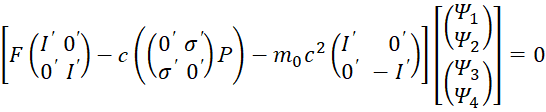, (24)

При этом матрицы имеют вид:

, (25)

Тогда, разбивая (24) на два матричных уравнения с двухрядными матрицами, получаем вместо одного уравнения с четырёхрядными матрицами два уравнения с двухрядными матрицами:

, (26)

Напомним, что при переходе к стационарному случаю и независимости электрического и магнитного поля от времени Дираком используется волновая функция для стационарного случая в виде:

Ψ(t,r) = exp [‒i/ћ(E+m₀c²)t] Ψ_r(r), (27)

Подставляя (27) в (26), и сокращая все члены уравнения на временной множитель exp [‒i/ћ(E+m₀c²)t], получим:

, (28)

, (29)

Из последнего уравнения следует:

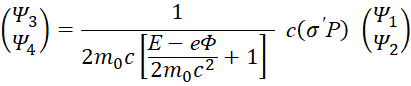, (30)

Далее принимается во внимание, что:

E‒eФ = m₀v ²/2, (31)

Отсюда при малых скоростях v/c << 1 имеем;

(E‒eФ) / (2m₀с²)=(m₀v²/2) / (2m₀с²)<<1, (32)

Тогда из (30) найдём:

, (33)

Подставляя (33) в (28) получаем:

, (34)

Соответственно учитываются следующие преобразования:

, (35)

В результате имеем равенство:

, (36)

Далее подставляем значение:

, (37)

Отсюда находим:

, (38)

Учитывая, что оператор p действует на все функции, стоящие справа от него, можем написать:

, (39)

Где Н = rotA – напряжённость магнитного поля; следовательно:

, (40)

Поэтому:

, (41)

Таким образом, уравнение Дирака при учёте членов, пропорциональных только v/c, переходит в уравнение Паули:

[E‒eФ‒P²/(2m₀) ‒ећ/(2m₀c) (σʹН)]Ψ = 0, (42)

На основании полученного результата утверждается, что появляется дополнительное выражение для энергии электрона в магнитном поле:

V^магн = ‒mH = ‒ећ/(2m₀c) (σʹН), (43)

Оно автоматически приводит к существованию магнитного момента электрона, величина которого в теории Паули постулировалась, исходя из анализа экспериментальных данных:

m = ећ/(2m₀c)σʹ, (44)

Далее мы покажем, что данный подход является чистейшей подгонкой под результат. С этой целью более подробно разберём расширение дифференциальных операторов в виде (23), и проведём с учётом них соответствующие преобразования, при подстановке одних уравнений в другие.

Физически введение дополнительно зависимости от векторных потенциалов означает, что значения энергии и импульса определяются распределением полей вектор-потенциалов в пространстве помимо значений энергии и импульса в волновой функции Шрёдингера вида Ψ(t, r) = exp[‒i/ћ (Еt‒Рr)] = exp[‒i/ћ (Еt‒Р_xx‒Р_yy‒Р_zz)].

В этом случае система уравнений Дирака может быть записана в виде [12, с. 353]:

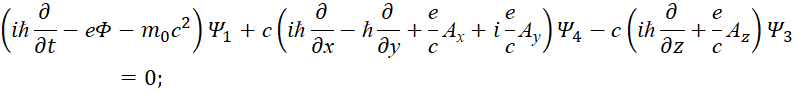
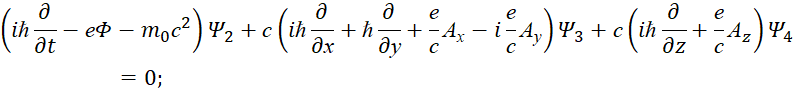
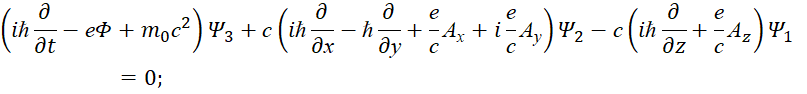
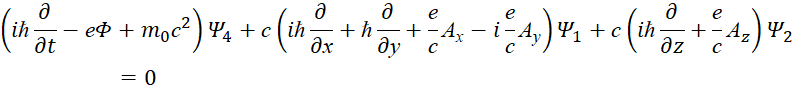, (45)

Если использовать волновую функцию (27), c учётом операции дифференцирования по Ψ, имеем:

(Е‒eФ)Ψ₁=cP_xΨ₄+eA_xΨ₄+icP_yΨ₄+ieA_yΨ₄‒cP_zΨ₃‒eA_zΨ₃;

(Е‒eФ)Ψ₂=cP_xΨ₃+eA_xΨ₃‒icP_yΨ₃‒ieA_yΨ₃+cP_zΨ₄+eA_zΨ₄;

(Е‒eФ+2m₀c²)Ψ₃=cP_xΨ₂+eA_xΨ₂+icP_yΨ₂+ieA_yΨ₂‒cP_zΨ₁‒eA_zΨ₁;

(Е‒eФ+2m₀c²)Ψ₄=cP_xΨ₁+eA_xΨ₁‒icP_yΨ₁‒ieA_yΨ₁+cP_zΨ₂+eA_zΨ₂, (46)

Дальше делается предположение, что скорость частицы определяется величиной энергии по формуле (31) в виде E‒eФ=m₀v²/2. При этом значение импульса незначительное (m₀v²/2)/(2m₀с²)<<1 в соответствии с (23), и, имеет только радиальную составляющую к центрально-симметричному электрическому полю. Отсюда получается система:

(Е‒eФ)Ψ₁=cP_xΨ₄+eA_xΨ₄+icP_yΨ₄+ieA_yΨ₄‒cP_zΨ₃‒eA_zΨ₃;

(Е‒eФ)Ψ₂=cP_xΨ₃+eA_xΨ₃‒icP_yΨ₃‒ieA_yΨ₃+cP_zΨ₄+eA_zΨ₄;

(2m₀c²)Ψ₃=cP_xΨ₂+eA_xΨ₂+icP_yΨ₂+ieA_yΨ₂‒cP_zΨ₁‒eA_zΨ₁;

(2m₀c²)Ψ₄=cP_xΨ₁+eA_xΨ₁‒icP_yΨ₁‒ieA_yΨ₁+cP_zΨ₂+eA_zΨ₂, (47)

Но, в этом случае мы имеем неоднозначность в определении энергии импульса частицы. С одной стороны энергия определяется величинами, стоящими справа от знака равенства в (47) по величинам cP_x, eA_x, icP_y, eA_y, cP_z и eA_z. А с другой стороны, энергия импульса (а она связана со скоростью движения, то есть кинетической энергией), исходя из допущений, сделанных в левой части от знака равенства. Другими словами, эта энергия была принята равной величине E‒eФ=m₀v²/2 в первых двух уравнениях (47). Однако, данное допущение имеет парадокс, так как величина E‒eФ=m₀v²/2 относится к формированию радиального значения скорости и имеет максимальное значение при eФ = 0. Собственно данный вариант относится к одномерному движению частицы при отсутствии постоянного значения скорости при движении по окружности. В оставшихся двух нижних уравнениях энергия слева от знака равенства в (47) равна константе (2m₀c²), то есть считается, что величина (E‒eФ)/m₀с²=(m₀v²/2)/(m₀с²)=0. При этом eФ максимально в месте нахождения ядра атома.

Фактически, как будет показано ниже, данный вариант эквивалентен иному представлению функций Ψ₁, Ψ₂ и Ψ₃, Ψ₄ в системе уравнений Дирака с аналогичным результатом.

Продолжим рассматривать противоречия, которые были допущены физиками при описании перехода к уравнению Паули. Теперь, соответственно, выразим одни функции Ψ₃, Ψ₄ через другие Ψ₁, Ψ₂, как это делается в системе уравнений Дирака без внешних сил. Отсюда имеем:

Ψ₃=(cP_xΨ₂+eA_xΨ₂+icP_yΨ₂+ieA_yΨ₂-cP_zΨ₁‒eA_zΨ₁)/(2m₀c²);

Ψ₄=(cP_xΨ₁+eA_xΨ₁‒icP_yΨ₁‒ieA_yΨ₁+cP_zΨ₂+eA_zΨ₂)/(2m₀c²), (48)

Далее мы должны провести действия по подстановке одних уравнений в другие для функции Ψ₁ в виде:

(Е‒eФ)Ψ₁=[cP_x(cP_xΨ₁+eA_xΨ₁‒icP_yΨ₁‒ieA_yΨ₁+cP_zΨ₂+eA_zΨ₂)+

+eA_x(cP_xΨ₁+eA_xΨ₁-icP_yΨ₁‒ieA_yΨ₁+cP_zΨ₂+eA_zΨ₂)+

+icP_y(cP_xΨ₁+eA_xΨ₁-icP_yΨ₁‒ieA_yΨ₁+cP_zΨ₂+eA_zΨ₂)+

+ieA_y(cP_xΨ₁+eA_xΨ₁-icP_yΨ₁‒ieA_yΨ₁+cP_zΨ₂+eA_zΨ₂)‒

‒cP_z(cP_xΨ₂+eA_xΨ₂+icP_yΨ₂+ieA_yΨ₂‒cP_zΨ₁‒eA_zΨ₁)‒

‒eA_z(cP_xΨ₂+eA_xΨ₂+icP_yΨ₂+ieA_yΨ₂-cP_zΨ₁‒eA_zΨ₁)] / (2m₀c²), (49)

На следующем этапе проводим перемножение членов:

(Е‒eФ)Ψ₁=[c²P_x²Ψ₁+ecP_xA_xΨ₁-ic²P_xP_yΨ₁‒iecP_xA_yΨ₁+c²P_xP_zΨ₂+

+ecP_xA_zΨ₂+ecA_xP_xΨ₁+e²A_x²Ψ₁-iecA_xP_yΨ₁‒

‒ie²A_xA_yΨ₁+ecA_xP_zΨ₂+e²A_xA_zΨ₂+ic²P_yP_xΨ₁+iecP_yA_xΨ₁+c²P_y²Ψ₁+

+ecP_yA_yΨ₁+ic²P_yP_zΨ₂+iecP_yA_zΨ₂+iecA_yP_xΨ₁+ie²A_yA_xΨ₁+

+ecA_yP_yΨ₁+e²A_y²Ψ₁+iecA_yP_zΨ₂+ie²A_yA_zΨ₂-c²P_zP_xΨ₂‒

‒ecP_zA_xΨ₂-ic²P_zP_yΨ₂-iecP_zA_yΨ₂+c²P_z²Ψ₁+ecP_zA_zΨ₁‒

‒ ecA_zP_xΨ₂‒e²A_zA_xΨ₂‒iecA_zP_yΨ₂‒ie²A_zA_yΨ₂+ecA_zP_zΨ₁+

+e²A_z²Ψ₁] / (2m₀c²), (50)

Соответственно приходим к виду:

(Е‒eФ)Ψ₁=[c²P_x²Ψ₁+c²P_y²Ψ₁+c²P_z²Ψ₁+e²A_x²Ψ₁+e²A_y²Ψ₁+e²A_z²Ψ₁‒

‒ic²P_xP_yΨ₁+ic²P_yP_xΨ₁+c²P_xP_zΨ₂‒c²P_zP_xΨ₂+ic²P_yP_zΨ₂‒

‒ic²P_zP_yΨ₂+ecP_xA_xΨ₁+ecA_xP_xΨ₁+ecP_yA_yΨ₁+ecA_yP_yΨ₁+

+ecP_zA_zΨ₁+ecP_zA_zΨ₁-ie²A_xA_yΨ₁+ie²A_yA_xΨ₁+ie²A_yA_zΨ₂‒

‒ie²A_zA_yΨ₂+e²A_xA_zΨ₂‒e²A_zA_xΨ₂+ecP_xA_zΨ₂‒ ecA_zP_xΨ₂+

+ecA_xP_zΨ₂‒ecP_zA_xΨ₂+ecA_xP_zΨ₂‒ecP_zA_xΨ₂ +

+iecP_yA_zΨ₂‒iecA_zP_yΨ₂+iecA_yP_zΨ₂‒iecP_zA_yΨ₂‒

‒iecA_xP_yΨ₁+iecP_yA_xΨ₁] / (2m₀c²), (51)

В конечном итоге получаем:

(Е‒eФ)Ψ₁=[c²P_x²Ψ₁+c²P_y²Ψ₁+c²P_z²Ψ₁+e²A_x²Ψ₁+e²A_y²Ψ₁+e²A_z²Ψ₁+

+ecP_xA_xΨ₁+ecA_xP_xΨ₁+ecP_yA_yΨ₁+ecA_yP_yΨ₁+

+ecP_zA_zΨ₁+ecP_zA_zΨ₁]/ (2m₀c²)=

=[c²P_x²Ψ₁+c²P_y²Ψ₁+c²P_z²Ψ₁+e²A_x²Ψ₁+e²A_y²Ψ₁+e²A_z²Ψ₁+

+2ecP_xA_xΨ₁+2ecP_yA_yΨ₁+2ecP_zA_zΨ₁] / (2m₀c²), (52)

Мы видим, что после исключения подобных членов с противоположными знаками остаются только величины импульсов по координатам в квадрате, значение вектор – потенциала по координатам в квадрате и произведение величин импульсов на значение вектор потенциалов по одинаковым координатам x, y, z. Отсюда имеем:

(Е‒eФ)Ψ₁=[c²P_x²Ψ₁+c²P_y²Ψ₁+c²P_z²Ψ₁+e²A_x²Ψ₁+e²A_y²Ψ₁+e²A_z²Ψ₁+2ecP_xA_xΨ₁+2ecP_yA_yΨ₁+2ecP_zA_zΨ₁] / (2m₀c²), (53)

Аналогичный вид будет и для функции Ψ₂. Понятно, что данный вид не соответствует тому, что получили физики в (42). Противоречие здесь и в том, что мы получили члены e²A_x²Ψ₁+e²A_y²Ψ₁+e²A_z²Ψ₁, которые не относятся к движению нашей частицы во внешнем магнитном поле. Эти члены относятся к независимому внешнему полю, которое никак не выражает магнитное взаимодействие с частицей. При этом взаимодействие внешнего поля (е/с)А с импульсом частицы имеет удвоенное значение в виде: 2ecP_xA_xΨ₁+2ecP_yA_yΨ₁+2ecP_zA_zΨ₁, а это не соответствует воздействию внешней магнитной силы по закону Лоренца, как это будет видно несколько ниже. Следует отметить, что при удалении произведений импульса Р на векторный потенциал (е/с)А, что кстати было фактически сделано Дираком при преобразовании от (36) к (39), имеем формулу:

(Е‒eФ)Ψ₁=[P_x²Ψ₁+P_y²Ψ₁+P_z²Ψ₁] / (2m₀)+[e²A_x²Ψ₁+e²A_y²Ψ₁+e²A_z²Ψ₁] / (2m₀c²), (54)

Видно, что уравнение (54) характеризует как бы два независимых уравнения Гамильтона-Якоби, которые определяют две независимые частицы. Одна частица характеризуется значениями Е и Р, а другая частица значениями еФ и (е/с)А. Отсюда понятно, что для описания взаимодействия движущейся частицы во внешнем электромагнитном поле надо иметь помимо члена характеризующего влияние электрического поля еФ, член характеризующий взаимодействие, который бы соответствовал воздействию магнитной силы Лоренца.

Так как вид уравнений, а также аргументы волновых функций, предложенных Дираком дают парадоксы, то это означает, что в системе уравнений Дирака, аргументы волновых функций и матрицы в системе уравнений для значений векторных потенциалов Ф и А по координатам должны иметь иной вид, который приводил бы к формированию реальных внешних сил определяющих движение частицы.

Надо отметить ещё раз, что физики естественно видели указанные парадоксы при непосредственной подстановке уравнений в системе Дирака и попытались уйти от классики. С этой целью они сделали подгонку под результат, приведённую выше по формулам (28–44). Однако, это оказалось связано со следующими алогизмами допущенными физиками. Первое, это то, что сделана подмена выражений и вместо значения для подобных членов с противоположными знаками в виде равенств нулю в (21), мы видим для тех же членов в (35) иное значение не равное нулю, что видно из сравнения:

;

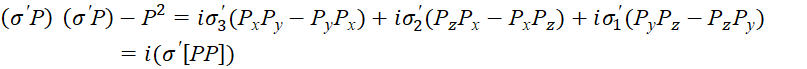, (55)

Во втором уравнении в (55) было использовано правило преобразования матриц в виде:

, (56)

В итоге для второго уравнения в (55) имеем:

, (57)

Таким образом, мы имеем совпадение первого и второго уравнения в (55), однако при совпадении результатов второе уравнение должно давать неравенство из-за перестановки значений импульсов по координатам, а первое уравнение ‒ нет. Как это может быть, если наличие неравенства в первом и втором уравнениях в (55) исключает получение корпускулярных свойств в системе уравнений Дирака по (21)?

Можно было бы с таким подходом согласиться, если бы внешнее электромагнитное поле на основе векторных потенциалов зависело бы от значений импульсов как операторов, дающих изменения на внешнее электромагнитное поле, но это в формулах (23) не предусматривается.

Однако это физиков не остановило, и было сделано ещё одно второе допущение на основе операторов в виде уравнений (38) и (37). Причём оказалось, что оператор импульса р должен был воздействовать неким образом на величину вектор – потенциала А, который является внешней количественной характеристикой по координатам, с превращением его в ротор . Иными словами, оператор импульса р уже не относится к частице с воздействием на волновую функцию Ψ, а относится и воздействует на внешнее поле А с его изменением и превращением его в ротор. Таким образом, мы имеем вторую очевидную подгонку под результат! Отсюда следует, что прежде, чем правильно характеризовать влияние внешних сил на корпускулярно-волновой объект, мы вначале должны определить взаимодействие и вид функций Дирака с переходом к уравнению Гамильтона-Якоби для свободно движущейся частицы. При этом нам надо разобраться с причинами образования знаков противоположных зарядов, которые у нас характеризуют излучение и поглощение, так как мы получаем одинаковый вид уравнений энергии Эйнштейна для противоположных функций Ψ₁ и Ψ₂ по системе (45). Понятно, что, при учёте компенсации вида (E‒eФ)/m₀с²=(m₀v²/2)/(m₀с²)=0 и при отсутствии векторного потенциала (е/с)А, мы получим вариант без учёта внешних полей. Тогда уравнение (54), с учётом сокращения на волновую функцию Ψ, будет связывать энергию и импульс в виде:

Е=[P_x²+P_y²+P_z²] / (2m₀)=P²/ (2m₀)=m₀V ²/2, (58)

Таким образом, изменив первоначальную функцию вида для свободно движущейся частицы на функцию вида Ψ(t,r)=exp[‒i/ћ(E+m₀c²)t]Ψ_r(r), Дирак показал возможность перехода к частному решению уравнения Гамильтона-Якоби. Правда, при этом он не избежал парадоксов, обозначенных нами выше.

Понятно, что нам надо заменить интуитивный подход Дирака с наличием парадоксов на переход к уравнению Гамильтона-Якоби без парадоксов.

Если исходить из системы самих уравнений Дирака (26), то они уже сами неоднозначно характеризуют преобразование волновой функции Ψ как объекта относительно первой и второй пары системы уравнений (26). Так как в одном случае в первую пару уравнений входит значение ‒m₀c², а во вторую пару уравнений (26) значение m₀c². Это означает, что при одинаковом виде волновых функций, равенство относительно одних уравнений, характеризующих одну противоположность объекта, будет означать неравенство касательно уравнений, характеризующих другую противоположность объекта. Однако данная система уравнений при использовании представления объекта в виде , обеспечила замкнутый вид взаимодействия противоположностей для свободно движущихся частиц при подчинении уравнению энергии Эйнштейна в квадрате.

Повторим, чтобы исключить полностью замкнутый вид, и перейти к взаимодействию с учётом внешних сил Дирак использовал иное представление объекта в виде новой волновой функции вида Ψ_д(t,r)=exp[‒i/ћ(E+m₀c²)t]Ψ_r(r). По сути, Дирак представил объект в виде новой волновой функции за счёт внесения значения m₀c². Таким образом, объект в виде волновой функции Ψ_д в противоположностях в системе уравнений Дирак поменял само взаимодействие противоположностей, что привело к некоторому соответствию с уравнением Гамильтона-Якоби для движущейся частицы. Надо отметить, что движущаяся частица по уравнению Гамильтона-Якоби также должна характеризоваться при взаимодействии электрической силой и магнитной силой, так как иного взаимодействия не предусмотрено. Поэтому, если учесть что по СТО и ОТО Эйнштейна , а [13, с. 235], то после подстановки в (58) и с учётом связи силы Кулона (электрической силы) и силы Лоренца (магнитной силы) [14, с. 273] в соответствии с электромагнитным континуумом, имеем:

, (59)

В этом случае коэффициент, равный двойке не даёт полную компенсацию между силами Кулона и Лоренца, которая должна соответствовать полной замкнутости на основании преобразований Лоренца-Минковского, с учётом перехода в уравнение окружности. Отметим, что уравнение окружности может быть преобразовано и в уравнение энергии Эйнштейна в квадрате. А это означает, что формула (58) не учитывает полное взаимодействие сил. Здесь не хватает взаимодействия, которое бы учитывало вторую половину кинетической энергии, и которая, кстати, должна формироваться с учётом внешних сил. В этом случае состояние частицы будет стабильное без распада. Иными словами, необходимо учитывать влияние от противоположности при взаимодействии.

Понятно, что данное противоречие не могло не отразиться на практике реальных опытов, что, кстати, и привело к открытию у элементарных частиц магнитного спина, который фактически определил учёт взаимодействия от противоположности.

Попробуем на основании нашей теории разрешить указанное противоречие, используя то, что уже применялось в квантовой механике, но имело иное толкование. Для этого более детально рассмотрим используемое в квантовой механике уравнение Шрёдингера. При этом мы учитываем, что уравнение Шрёдингера с учётом внешних сил будет иметь вид [15, с. 30]:

, (60)

Собственно, Шрёдингер попытался объединить чисто корпускулярное уравнение Гамильтона-Якоби на основе второго закона Ньютона с сочетанием при этом волновых свойств и внешнего воздействия U. Для этого он использовал нормировку на постоянную Планка и умножение первой производной от функции по времени на мнимую единицу. Соответственно, возведение в квадрат первой производной от функции по длине он заменил интуитивно двойным дифференцированием этой функции. В итоге волновой вид комплексной функции позволил получить решение аналогичное тому, какое следовало для уравнения Гамильтона-Якоби от второго закона Ньютона. Собственно совпадение решения для волновой функции с решением для функции для корпускулярной частицы означает возможность сочетания корпускулярных и волновых свойств в одном общем объекте. Но вид уравнений при этом оказался отличающимся. Тогда физики посчитали, что данное уравнение Шрёдингера должно удовлетворять условию, при котором оно должно в предельном случае переходить в уравнение Гамильтона-Якоби. С этой целью вместо волновой функции Ψ вводят функцию S при помощи соотношения [15, с. 30]:

, (61)

Далее учитывают равенства:

, (62)

Так как волновая функция Ψ входит во все члены лишь множителем, то её можно сократить, тогда получим:

, (63)

В предельном случае физики полагают, что при , данное уравнение переходит в уравнение Гамильтона-Якоби. Однако надо напомнить, что , а это означает, что перехода к уравнению Гамильтона-Якоби просто быть не может, так как нет варианта, при котором . В противном случае при , получается однородность, нарушаются законы физики и, соответственно нет и самих противоположностей. Кроме того, в дальнейшем это уравнение (63) используется при методе Вентцеля-Крамерса-Бриллоэна (метод ВКБ) для сшивания функций на границе раздела с получением в конечном итоге правила квантования Бора-Зоммерфельда, на основании чего оправдывался туннельный эффект с прохождением через потенциальный энергетический барьер, а также наличие нулевой энергии по соотношению неопределённостей Гейзенберга. При этом исчезновения члена с величиной постоянной Планка исключало доказательство всех остальных преобразований. Парадоксы таких решений мы также подробно рассмотрели в [16, с. 5-27].

Понятно, что перехода к уравнению Гамильтона-Якоби от уравнения Шрёдингера в принципе быть не могло, так как это бы давало бы одинаковый результат при наличии разного воздействия на объект.

Однако попытаемся понять, есть ли возможность перехода от уравнения Шрёдингера с волновой функцией Ψ к корпускулярному движению частицы, как это получилось для системы уравнений Дирака. Повторим, что суть отличия уравнения Шрёдингера от уравнения Гамильтона-Якоби, в том, что Шрёдингер ввёл двойное дифференцирование функции по длине, вместо возведения в квадрат значения первой производной от функции как в уравнении Гамильтона-Якоби. В этом случае с учётом того, что при взаимодействии через обмен (это выражается в изменениях) участвуют обе противоположности, которые в данном случае выражены через значения аргумента и функции, возведение в квадрат как это показано в (59) происходит на основании правил дифференцирования в математике с учётом закона сохранения количества. Таким образом, мы видим, что нормировочный коэффициент , в аргументе функции Ψ был необходим физикам для обоснования подгонки под результат перехода от уравнения Шрёдингера к уравнению Гамильтона-Якоби. Однако мы учитываем, что постоянная Планка ‒ это просто нормировочный коэффициент и его можно не учитывать, если рассматривать волновую функцию вида:

, (64)

Именно такой вид функции мы использовали при переходе от волновых свойств электромагнитных функций к корпускулярным свойствам на основании усовершенствованных уравнений Максвелла в [1, с. 5-36]. Отметим также, что уравнение Шрёдингера в нашем случае с учётом правила (16), введённого Дираком, и наличием электромагнитных функций необходимо представить в виде, которое соответствует уравнению Гамильтона-Якоби без учёта внешних сил:

, (65)

Иными словами, волновая функция Ψ по (64) соответствует решению уравнения Гамильтона-Якоби, без добавочного умножения первой производной по времени на мнимую единицу, если учесть введённое Дираком правило (16), без которого переход от волновых свойств к корпускулярным свойствам был бы невозможен. Собственно, по логике нашей теории операции дифференцирования (интегрирования) также связаны с умножением на мнимую единицу [5, с. 5-37]. В противном случае не будет перехода от волнового вида к корпускулярному виду, и наоборот, из-за отсутствия смены закономерностей и в силу того, что сложение в одной противоположности означает вычитание в другой противоположности. Повторяем ещё раз для оппонентов, что умножение на мнимую единицу при дифференцировании не наша выдумка, и было впервые применено интуитивно Дираком. Следует заметить, что добавочное дифференциальное изменение в уравнении Шрёдингера фактически означает, что это изменение даёт переход от функции, характеризующей корпускулярные свойства, к волновой электромагнитной функции. Более того отметим что нормировка волновой функции в виде: позволяет совместить волновые и корпускулярные свойства через уравнение с учётом того, что в нашей теории m₀=1/с. Иными словами, изменение в одной противоположности, что выражается изменением по времени, в противоположности выражается изменением по длине. И обратная реакция даёт противодействие первоначальному изменению через двойное дифференцирование. Понятно, что данный результат, совмещения волновых и корпускулярных свойств, получить на основе отсутствия связи массы с пространственно-временным искривлением, помимо нашей теории, было невозможно. То есть, корпускулярным свойствам, на основе уравнения Гамильтона-Якоби, соответствуют изменения волновых свойств на основе волновой функции вида с соблюдением закона противодействия на действие в виде . Иными словами, Шрёдингер, интуитивно, введя двойное дифференцирование по длине функции Ψ, тем самым осуществил переход к описанию движения через волновую функцию от противоположности с получением конечного результата, аналогичному для уравнения Гамильтона-Якоби. Однако, как мы показали выше в (59), мы имеем дисбаланс в формировании электрических и магнитных сил, что не соответствует замкнутой системе на основе уравнения окружности. Этот дисбаланс исключается для уравнения Гамильтона-Якоби за счёт наличия внешних сил. При этом мы имеем уравнение:

, (66)

Это уравнение имеет решение в виде:

, (67)

Иными словами, добавление в аргумент функции значения U позволяет учитывать воздействие внешних сил на частицу.

Соответственно, теперь надо разобраться, что, собственно, даёт учёт взаимодействия корпускулярных и волновых свойств при законе сохранения количества за счёт перехода от возведения в квадрат первой производной функции от длины в уравнении Гамильтона-Якоби к двойному дифференцированию по длине этой же функции. Если волновая функция Ψ имеет вид (64), то мы имеем уравнение Гамильтона-Якоби (65). Однако, если исходить из (62), то здесь учитывается и изменение самого аргумента. То есть уравнение Шрёдингера может рассматривать процесс во взаимосвязи противоположностей, а не в варианте наличия одной противоположности по волновой функции Ψ с видом (64). При этом должно соблюдаться условие закона сохранения количества, так как объект не исчезает в результате движения.

В нашем случае, с учётом электромагнитных функций [1, с. 5-36], мы будем иметь вид без нормировочного коэффициента в виде величины постоянной Планка:

, (68)

В итоге получаем равенства:

, (69)

С учётом (68) и поскольку волновая функция Ψ в результате данного преобразования должна входить во все члены лишь множителем, мы можем её сократить. В итоге получаем:

, (70)

Далее мы учитываем, что движению частицы в одной противоположности создаётся за счёт противодействия через движение частиц в другой противоположности в силу условия сохранения количества между противоположностями и необходимой при этом симметрии. В этом случае с учётом сохранения частицы в исходном виде (что видно из функции ) с правилом дифференцирования (16), мы получаем связь электрической силы и магнитной силы с полным подчинением преобразованиям Лоренца-Минковского при в виде:

, (71)

Иными словами, взаимодействие корпускулярных и волновых свойств по уравнению аналогичному уравнению Шрёдингера совпадает с результатом по системе уравнений Дирака для свободной частицы, выведенных из уравнения энергии Эйнштейна. Однако отличие в том, что в уравнении Шрёдингера аргумент функции выражается как изменяемая противоположность. В системе уравнений Дирака аргумент функции не имеет изменений. То есть данный вид уравнения (70) соответствует представлению волновых функций Ψ в системе уравнений Дирака в виде при переходе от волновых свойств к корпускулярным свойствам для свободного движения частицы с учётом исходного уравнения энергии Эйнштейна. Одновременно, мы видим, что в системе уравнений Дирака вариант представления волновой функции в виде (61) с возможностью изменения аргумента исключается в силу наличия только первых производных по времени и длине. При этом вариант замкнутого взаимодействия противоположностей в системе уравнений Дирака достигается за счёт функции вида . При свободном движении частицы, с соответствием уравнению энергии Эйнштейна, мы не имеем взаимодействия с внешними силами.

Чтобы решить задачу с внешними силами надо иметь замкнутый вид для частицы с учётом внешних сил. Такому внешнему влиянию на объект соответствует изменение состояния объекта на основе второго закона Ньютона с учётом получения уравнений (10) и (11). Иными словами, для учёта воздействия внешних сил с условием сохранения объекта надо получить из системы уравнений Дирака вид уравнения Гамильтона-Якоби. Сравнивая (71) с (59), мы видим, что уравнение Гамильтона-Якоби отражает отсутствие замкнутого вида в виде влияния от одной противоположности. Вот поэтому Дирак интуитивно применил функцию и добавил внешние силы через векторные потенциалы. Однако, как мы показали выше, данный способ даёт парадоксы с подгонкой под результат. Соответственно, отсюда следует необходимость найти такой вид функций в системе уравнений Дирака, который бы не имел указанных выше парадоксов.

С этой целью возвратимся вновь к уравнению (65). Мы видим, что при представлении волновой функции в виде , мы характеризуем объект без замкнутого взаимодействия. В этом случае волновые свойства по уравнению аналогичному уравнению Шрёдингера дают результат, соответствующий уравнению Гамильтона-Якоби. Понятно, что общий вид частицы в замкнутом режиме свободного движения с учётом волновых и корпускулярных свойств даёт вариант инвариантного уравнения (70), что видно из (71).

Учёт внешних сил изменяет энергию частицы, но внешние поля входят в уравнение Гамильтона-Якоби как независимые величины, и таким образом мы не учитываем обратное влияние частицы на эти внешние воздействия. Однако и в этом случае частица имеет замкнутый вид взаимодействия между противоположностями, образующими саму частицу, что отражается через её значение импульса.

Рассмотрим принцип взаимодействия противоположностей в самой частице, который должен определяться через силовые воздействия, дающие обмен между противоположностями. В противном случае будет независимость противоположностей, и говорить о наличии общей частицы невозможно. С целью исключения парадоксов допущенных Дираком и на основании полученных замкнутых решений для уравнения аналогичного уравнению Шрёдингера с учётом изменения аргумента волновой функции вида в системе уравнений Дирака мы используем функцию , так как масса ‒ это константа, и она в динамике взаимодействия не участвует. После подстановки данной функции в (70), как эквивалента системы уравнений Дирака по результату в случае свободного движения частицы, мы получим:

, (72)

В этом случае мы имеем сочетание противоположностей в одной частице в виде:

, (73)

Иными словами, мы имеем два уравнения, соответствующие по результату уравнению Гамильтона-Якоби с отражением взаимодействия противоположностей в корпускулярном и волновом виде. Верхнее уравнение в (73) определяет соответствие энергии силам взаимодействия, характеризующим обменные процессы в самой частице. В нижнем уравнении мы имеем пространственно-временное искривление , исходя из скорости движения частицы в противоположности. Если исходить из того, что энергия частицы может быть как положительной, так и «отрицательной» (в соответствии с теорией Дирака), что выражается в смене знака перед членом , то в этом случае исходным будет функция вида . При этом поменяется знак с плюса на минус перед , во втором уравнении (73).

Ещё раз подчеркнём, что вариант (72) описывает взаимодействие по уравнению Гамильтона-Якоби внутри самой частицы. При этом вид (72) был нами получен на основе аналога уравнения Шрёдингера с учётом изменения аргумента волновой функции в виде . Кроме того, мы видим, что при функции , без учёта изменения аргумента волновой функции мы получаем частный вариант в виде уравнения (66), которое отражает решение с учётом внешнего поля. Иными словами, уравнение аналогичное уравнению Шрёдингера, с учётом изменения аргумента функции за счёт двойного дифференцирования, может отражать как внутреннее замкнутое взаимодействие частицы, так и замкнутое взаимодействие с учётом внешнего воздействия с учётом энергетического баланса.

Однако, так как в системе уравнений Дирака не используется вариант с двойным дифференцированием и есть подгонки под результат, допущенные Дираком с наличием парадоксов, то становится понятно, что использование одинакового вида функций не даёт перехода к уравнению Гамильтона-Якоби с наличием внешних сил через систему уравнений Дирака. Но в силу того, что в [1, с. 5-36] мы показали, что система уравнений Дирака с учётом замены волновых функций, характеризующих вероятность, на электромагнитные функции, так же как и уравнение (70), даёт соответствие уравнению энергии Эйнштейна, то такой переход к уравнению Гамильтона-Якоби должен существовать. Иначе переход от волновых свойств к корпускулярным свойствам принципиально не мог бы быть.

Необходимость такого описания перехода к уравнению Гамильтона-Якоби в том, что уравнение Гамильтона-Якоби не даёт, в отличие от системы уравнений Дирака, описание перехода от простейших электронных и мюонных нейтрино и антинейтрино (усовершенствованных уравнений Максвелла) как к волновым, так и к корпускулярным свойствам. То есть из аналога уравнения Шрёдингера (70) такого перехода от простого варианта к сложному варианту, получить нельзя. Однако, если есть переход от электромагнитных функций к свободному движению частицы, а результаты перехода к уравнению Гамильтона-Якоби получаются через аналог уравнения Шрёдингера, которое учитывает волновые свойства, то аналогичный вариант перехода должен быть и для системы уравнений Дирака. Тем более, что результаты для свободного движения частицы совпадают. Поэтому, чтобы получить аналогичные зависимости на основе уже системы уравнений Дирака и удовлетворить условию получения чистого соответствия с уравнениями Гамильтона-Якоби в противоположностях, необходимо иметь разное представление волновых функций для первой и второй пары в системе уравнений (26), которые отражают противоположности. Тогда для системы уравнений Дирака мы имеем следующий вид Ψ-функций в виде:

Ψ₁=exp[‒i(Et+mc²t‒P_xx‒P_yy‒P_zz)];

Ψ₂=exp[‒i(Et+mc²t‒P_xx‒P_yy‒P_zz)];

Ψ₃=exp[‒i(mc²t‒P_xx‒P_yy‒P_zz)];

Ψ₄=exp[‒i(mc²t‒P_xx‒P_yy‒P_zz)], (74)

Иными словами, для перехода в системе уравнений Дирака к уравнению Гамильтона-Якоби, мы изменили первые две волновые функции по аналогии с тем, как это сделал Дирак (это также следовало из удовлетворения уравнению (72)), а две последние функции фактически оставили в первоначальном виде . По сути, это соответствует представлению частицы в виде взаимодействия разомкнутой и замкнутой системы. То есть частица состоит из противоположностей. В этом случае, без учёта внешних сил, мы имеем систему уравнений Дирака в виде:

, (75)

Мы видим, что вид первых двух функций Ψ₁ и Ψ₂ соответствует волновому виду аналогично (17) и при этом энергия волны определяется величиной mc². Нижние две Ψ-функции Ψ₃ и Ψ₄ определяют фактически условие формирования излучения от величины mc² аналогично по формуле (27). В итоге имеем:

, (76)

Выразим одни функции через другие:

, (77)

Далее осуществляем подстановку функций:

, (78)

Иными словами, мы получаем уравнение Гамильтона-Якоби без внешних сил. Надо отметить, что если мы выберем вариант функций в виде:

Ψ₁=exp[‒i(‒mc²t‒P_xx‒P_yy‒P_zz)];

Ψ₂=exp[‒i(‒mc²t‒P_xx‒P_yy‒P_zz)];

Ψ₃=exp[‒i(Et‒mc²t‒P_xx‒P_yy‒P_zz)];

Ψ₄=exp[‒i(Et‒mc²t‒P_xx‒P_yy‒P_zz)], (79)

Получим решение для волновой функции Ψ₃ в виде:

, (80)

Это соответствует теории Дирака о наличии положительных и «отрицательных» энергий для частицы, что, собственно, и определяет представление противоположностей в виде длины и времени как противоположных зарядов.

Для учёта внешних электромагнитных сил необходимо учитывать физический смысл их воздействия на частицу. Само уравнение Гамильтона-Якобы уже способно определять детерминированное движение частицы, так как выводится из (10). Однако здесь требуется знать принцип образования внешних сил, воздействующих на частицу. В нашем случае ‒ это сила Кулона и сила Лоренца. Если исходить из принятого в физике представления этих сил, то для электрической силы, которая влияет на изменение импульса частицы, мы имеем:

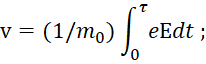
, (81)

Здесь Е ‒ напряжённость электрического поля, е – заряд частицы.

В данном случае электрическая сила учитывает воздействие на частицу с массой m₀, где сила Кулона эквивалентна ускорению и это следует из первого уравнения (81). Собственно, в противном случае мы не имеем реального представления, так как будет получаться, что сила Кулона ‒ это нечто отдельное от пространства и времени. Магнитная сила образуется в результате движения частицы в магнитном поле, и мы имеем закон:

, (82)

Здесь В – магнитная индукция и также учитывается, что по нашей теории m₀=1/c, а Н=сЕ.

Кроме того, мы в [1, с. 5-36] показали, что константы электрической и магнитной проницаемости зависят от кинетической энергии в противоположности, и эта зависимость выражается через обобщённое и усреднённое значение скорости частиц в противоположности v_пр. Как мы неоднократно отмечали, эти две силы противодействуют друг другу с учётом изменений в противоположностях. С учётом преобразования электрических сил в магнитные силы, и наоборот, и их противодействия друг другу, мы можем записать:

, (83)

Отсюда можно установить, что равенство сил в стационарном случае движения частицы будет при достижении некоторой тангенциальной скорости при условии:

, (84)

Иными словами, мы получаем уравнение окружности на основе значения скоростей в противоположностях Мироздания, из которого следует, что равенство силы действия и противодействия определяется значением обобщённой кинетической энергией в противоположности на основании . Понятно, что в этом случае будет движение частицы по окружности (электрона вокруг протона) с тангенциальной скоростью v. Так как мы имеем замкнутое преобразование между электрической и магнитной силой, на основе закона сохранения количества, то ничего иного в формулу наличия только этих сил вставить нельзя. Более того, отсюда следует, что законы Кулона и Лоренца ‒ это результат отражения пространственно-временного искривления по СТО и ОТО Эйнштейна.

В [5, с. 5-37] мы показали, что аналогичный переход к уравнению окружности дают и преобразования Лоренца, а также уравнение энергии Эйнштейна.

Если исходить из уравнения Гамильтона-Якоби, то при построении детерминированного движения частицы мы должны знать значения этих сил в каждой точке на протяжении всего маршрута, и по формулам (81) и (82) вычислять пройденный маршрут от одной точки пространства к другой по формуле:

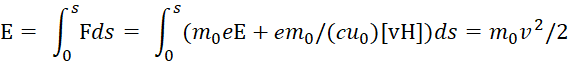, (85)

Отсюда следует вывод, что при наличии известных значений констант электрической и магнитной проницаемости, и амплитудных значений напряжённостей электрических и магнитных полей с учётом скорости в точках пространства в данный момент времени можно определять детерминированное движение частицы.

Собственно, здесь нет ничего нового, и именно так сейчас рассматривается движение частицы в электромагнитном поле. Однако сам принцип существования силы Лоренца и Кулона не был связан с взаимодействием противоположностей Мироздания, так как для этого надо было показать связь констант электрической и магнитной проницаемости с наличием кинетической энергии в противоположности с переходом кинетической электромагнитной энергии в потенциальную энергию пространственно-временного искривления по СТО и ОТО Эйнштейна. С учётом выбранных систем измерения СИ или СГС это было сделать невозможно.

Снова отметим, что уравнение Гамильтона-Якоби при вычислении детерминированного движения частицы за счёт знания наличия сил и скорости в каждой точке пространства учитывает также и наличие излучения и поглощения энергии частицей при равноускоренном движении. Однако как происходит этот процесс излучения и поглощения не был понятен в квантовой механике, так как волновые функции Ψ, характеризующие вероятность не были связаны с электромагнитными составляющими напряжённостей полей (вероятность с детерминированными процессами принципиально нельзя связать). Кроме того, система уравнений Дирака с представлением воздействия внешних сил в соответствии с (23) и (42) вообще игнорирует излучение и поглощение как необходимый процесс в орбитальном движении частицы. С учётом связи системы уравнений Дирака с электромагнитными составляющими на основе взаимодействия электронных и мюонных нейтрино и антинейтрино по нашей теории, которые при взаимодействии также приводят к образованию электромагнитной волны [1, с. 5-36], мы получаем об этом представление за счёт смены составляющих напряжённостей электромагнитных полей в системе уравнений Дирака.

Другими словами, указанное нами воздействие определяется по смене величины и направления скорости движения частицы, и равенство сил действия и противодействия достигается за счёт учёт влияния движения в противоположности. При этом получается, что излучение в одной противоположности характеризует значения констант электрической и магнитной проницаемости в другой противоположности, и наоборот. В противном случае не соблюдался бы закон сохранения количества между противоположностями, и именно это исключает парадокс падения электрона на ядро.

Таким образом, мы видим, что задача движения частиц решается классическим методом в силу того, что через электромагнитные волновые функции в системе уравнений Дирака мы получаем корпускулярные свойства и классическое уравнение Гамильтона-Якоби.

Соответственно возникает вопрос: «А можно ли на основании системы уравнений Дирака получить аналогичный результат детерминированного движения частицы, исходя из того, что в соответствии с (78) и (80) мы получаем уравнение Гамильтона-Якоби?»

Отличие от уравнения (85) здесь в том, что в уже существующее уравнение Гамильтона-Якоби вносятся энергетические составляющие от внешнего электромагнитного поля. Здесь надо определиться, исходя из чего, при этом, будут вычисляться вторые составляющие в операторах (23) вида еФ и е/сА. Далее следует понять, в каких случаях данное уравнение имеет применение. Так как мы не знаем смысл данного уравнения с точки зрения применения на практике, а хотим получить эквивалентный конечный результат, то введём вместо еФ и е/сА значения W и G. При этом конечно должно выполняться условие того, что эти значения должны быть напрямую связаны с электрической силой и магнитной силой, так как никаких иных сил в Мироздании нет и другого способа получения или изменения энергии через силы не существует. Более того, электромагнитные функции, которые мы ввели вместо волновых функций, характеризующих вероятность, могут взаимодействовать только с электрическими и магнитными силами.

Одновременно система уравнений Дирака в виде первых двух уравнений отражает одну противоположность, а два последних уравнения ‒ отражают другую противоположность. Отсюда логично предположить, что первые два уравнения с учётом представленных нами волновых функций (74) должны характеризовать взаимодействие с электрическими силами, а два оставшихся с магнитными силами. То есть, таким образом, мы отражаем внешнее воздействие с учётом того, что в противоположностях электрическая и магнитная сила меняются местами. Как мы увидим далее, это даёт единственный способ получения дополнительно зависимости от электрических и магнитных сил на основе системы уравнений Дирака. К чему приводит иной вариант, предложенный Дираком, мы показали выше, и он даёт парадоксы.

Отсюда получаем следующий вид:

, (86)

После операции дифференцирования по функциям имеем:

, (87)

Аналогично, как и ранее, выразим одни функции через другие:

, (88)

В результате после подстановки функций имеем:

(89)

На следующем шаге мы должны определить значения W и G, которые в системе уравнений Дирака представлены величинами еФ и е/сА. В квантовой механике значение Ф при наличии воздействии на частицу единичного заряда определяется в виде:

, (90)

И это даёт парадокс отсутствия пространственно-временного искривления среды распространения, что определяется константами электрической и магнитной проницаемости. Поэтому, мы будем исходить из более обширного понимания электрической силы в виде известного уравнения [17, с. 119]:

, (91)

Здесь q=ne, где n ‒ количество заряженных частиц от внешнего поля. В соответствии с (85) должны иметь следующее значение:

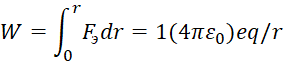, (92)

Вид формулы (90) отличается от вида (91) наличием учёта множителя и количеством внешних зарядов участвующих во взаимодействии q. Понятно, что в варианте (92) мы учитываем, что внешние заряды воздействуют на движущийся электрон через среду распространения, а она характеризуется электрической и магнитной проницаемостью. То есть среда имеет динамику изменения, иначе она бы не принадлежала Мирозданию как объект. В этом случае через среду не было бы взаимодействия. Понятно, что изменение энергетического состояния системы по (92) связано с изменением энергии W, что определяется изменением расстояния вдоль радиуса r. Однако такого изменения при вращении электрона вокруг протона не наблюдается, как и изменения скорости вращения. Отсюда добавление значения W или удаление значения W определяет только лишь значение кинетической энергии через скорость вращения v. В итоге получается, что влияния электрической силы на взаимодействие при вращении электрона вокруг протона нет, так как нет изменения электрической энергии при r=const. Такой вариант подходит только для описания статики при круговом движении частицы по орбите и в этом случае Бор использовал уравнение движение электрона в виде [7, с. 58-59]:

, (93)

В этой формуле есть только энергетический баланс. При этом Бор считал, что момент импульса электрона получается из уравнения гармонического осциллятора (3) и удовлетворяет условию:

, (94)

Однако и он не избежал парадокса, связанного с его постулатами, так как он ввёл запрет на излучение электроном на дискретных орбитах, в то время как по формуле (3) вычисление момента импульса электрона по формуле (94) связано именно с излучением.

Чтобы как-то обосновать внесение значения еФ и наличие влияния электрической силы на общую энергию частицы, Дирак в своей системе уравнений от двумерного варианта движения частицы вокруг протона был вынужден перейти к одномерному варианту по одной координате. Однако в этом случае он должен был решать задачу движения электрона вокруг протона отдельно по трём координатам длины с последующим получением объединённого решения. Такой вариант возможен при использовании трёх уравнений Гамильтона-Якоби по каждой из координат длины, но не в случае одномерного варианта использовано Дираком. В этом случае электрон должен телепортироваться через протон! Понятно, что ускоренное движение электрона по координатам длины неизбежно связано с излучением, как и для варианта гармонического осциллятора.

Для нахождения эквивалентности значения G по изменению магнитной силы, а значит и энергии в системе уравнений Дирака, мы, для описания взаимодействия через магнитную силу, будем исходить из равенств:

, (95)

Отсюда имеем значение магнитной силы для взаимодействия в виде:

, (96)

Иными словами, значение магнитной силы взаимодействия определяется через значения движения зарядов в виде токов. Собственно данный результат неотделимости движения частицы от магнитной силы связан с известным законом Био-Савара-Лапласа, с применением операции (rot) на основе стационарного магнитного поля. В электродинамике в дифференциальной форме он выражается в виде:

, (97)

Иными словами, всякое движение частицы со скоростью v (это может быть и вращение частицы) приводит к формированию замкнутого поперечного магнитного поля в некоторой точке пространства, выраженного в дифференциальной форме через ротор (rot). С точки зрения нашей теории это означает, что прямолинейное движение в одной противоположности означает замкнутое движение в другой противоположности. В противном случае между противоположностями нет отличий. Понятно, что известен также и обратный процесс, когда внешнее замкнутое магнитное поле приводит к формированию движения частицы (это видно по наличию тока в катушке индуктивности при отключении разности потенциалов электрического поля). Соответственно, известно уравнение Даламбера относительно векторного потенциала А, вывод которого мы показали в [1, с. 5-36], и это также было сделано в электродинамике [18, с. 119]:

, (98)

Суть наличия стороннего тока можно интерпретировать из классики электродинамики следующим образом. Пусть электрон движется со скоростью v по орбите r (рис.).

Рис. Движение электрона по орбите

Через площадку, расположенную в любом месте на пути электрона, перемещается в единицу времени заряд еv_об, где е – заряд электрона, а v_об число оборотов в секунду. Следовательно, движущийся по орбите электрон образует круговой ток силы I=ev_об. Поскольку заряд электрона отрицателен, направление движения электрона и направление тока противоположны. Магнитный момент создаваемого электроном тока равен:

, (99)

Произведение даёт скорость движения электрона v, поэтому можно написать:

, (100)

Момент по (100) обусловлен движением электрона по орбите, вследствие чего называется орбитальным магнитным моментом электрона. Направление вектора р_m образует с направлением тока правовинтовую, а с направлением движения электрона левовинтовую систему. Движущийся по орбите электрон обладает моментом импульса:

, (101)

Вектор L – называют орбитальным механическим моментом электрона. Он образует с направлением движения электрона правовинтовую систему. Следовательно, направления векторов р_m и L противоположны. Отношение магнитного момента элементарной частицы к её механическому моменту принято называть магнитомеханическим (или гиромагнитным) отношением. Для электрона с учётом связи скорости света с массой электрона оно равно;

, (102)

Учитывая, что в теории Дирака заряд элементарных частиц равен , то мы получаем, что поступательное движение электрона в одной противоположности определяет энергетический обмен в другой противоположности в статике величиной равной половине от максимума энергии. Собственно, это оправдывает нормировочный коэффициент с/2 в функции вида , что позволяет совместить волновые и корпускулярные свойства при учёте взаимодействия противоположностей вида . Однако, в данном варианте описания электрона мы учли его поступательное движение по орбите, но не учли его замкнутое (вращательное) движение (спин). Наличие спина определяет его как отдельный объект в Мироздании, и оно тоже связано с энергией. Учёт вращательного движения помимо поступательного движения отражён и в уравнении гармонического осциллятора (3), который используется Бором для получения момента импульса пропорционального значению величины постоянной Планка. Так как замкнутое движение в одной противоположности эквивалентно поступательному движению в другой противоположности с учётом закона сохранения количества, то значение гиромагнитного отношения для вращательного движения электрона ничем не отличается от расчёта орбитального момента. В итоге мы имеем значение общего стороннего тока в виде Иными словами, объект среды характеризуется обменом с максимальной энергией. Если учесть, что размер объекта среды распространения имеет размеры h=m₀=1/c, то получим характеристику объектов среды распространения как значение . В этом случае объекты среды распространения определяются через значение константы магнитной проницаемости в (98). Как мы это неоднократно отмечали, константа магнитной проницаемости в соответствии с СТО и ОТО Эйнштейна определяется движением частиц в противоположной системе наблюдения. В этом случае константа магнитной проницаемости определяет параметры волнового излучения на основе потенциальной энергии в каждой точке среды распространения в соответствии с принципом Гюйгенса-Френеля. При этом, решение уравнения (98), в волновом виде с соблюдением принципа Гюйгенса-Френеля соответствует гипотезе Луи де Бройля для представления объектов в виде волновых функций в том случае, если справа от знака равенства также присутствует значение векторного потенциала, как это было показано для волновой функции Ψ в [19, с. 30-31] и впервые введено Шрёдингером:

, (103)

В противном случае будет в конечном решении уравнения (98) также присутствовать волновая функция без возможности её сокращения. А это даст противоречие и отсутствие равенства. Отсюда имеем:

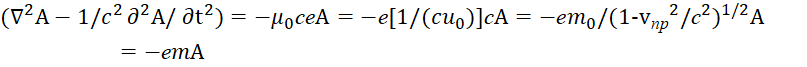, (104)

В данном случае мы рассматриваем изменения в среде распространения, которые влияют на движущуюся частицу на основе обобщённой и усреднённой кинетической энергии излучения от частиц в противоположности. Чтобы учесть воздействие в нашей системе наблюдения от наличия другой частицы на рассматриваемую движущуюся частицу надо вспомнить, что внешнее воздействие такой частицы характеризуется через векторные потенциалы Ф и А, на основе известной формулы связи векторных потенциалов из электродинамики [20, с. 165]:

, (105)

Здесь значение векторного потенциала Ф определяется по формуле:

, (106)

В этом случае вариант воздействия внешних сил на движущуюся частицу определяется через воздействие других частиц с учётом относительной скорости в общей системе наблюдения. Собственно иного описания воздействия частиц и их отличия не придумано. Так как значение константы электрической (магнитной) проницаемости мы уже учли в (104), то с учётом (104) и (105), мы получаем:

, (107)

На основе верхнего уравнения в (107) мы получаем связь движущейся частицы с излучением (поглощением) кинетической энергии. При этом перешли от зависимости излучения на основе сторонних токов от объектов среды распространения к описанию формирования импульса движения частицы (обычного тока) с получением или излучением волновой кинетической энергии. Это как раз никак не могли получить физики в электродинамике на основе (98). Дело в том, что они рассматривали векторные потенциалы при выводе волновых уравнений, аналогично электромагнитным составляющим, связанным через скорость света. Это видно из уравнений Даламбера в [18, с. 119], где переход от А к Ф даёт связь сА=Ф. Отсюда результат источников возбуждения мог выражаться только через сторонние токи в (98). В нашем случае мы учитываем, что волновые свойства в одной противоположности переходят в корпускулярные свойства в другой противоположности, и в этом случае векторные потенциалы имеют связь уже по уравнению (105), а не в виде сА=Ф. Следовательно, физикам, чтобы прийти к нашему результату, надо было учесть в (98), справа от знака равенства, наличие волновой функции по гипотезе Луи де Бройля, и также по этой же гипотезе учесть что корпускулярное движение в одной противоположности приводит к волновому процессу в другой противоположности, и наоборот, с учётом симметрии и закона сохранения количества в противоположностях. При этом необходимо вспомнить саму формулу Луи де Бройля [21, с. 63]:

, (108)

Как мы не раз показывали, эта формула выводится из аргумента волновой функции:

, (109)

Иными словами, формулой (107) мы лишь только подтвердили формулу Луи де Бройля, когда движение частицы с импульсом р в одной противоположности эквивалентно излучению с частотой f в другой противоположности. То есть, Луи де Бройль также интуитивно фактически ввёл излучение в противоположности для движущейся частицы в нашей системе наблюдения, так как в противном случае он получает парадокс наличия скорости распространения волны (u) выше скорости света исходя из формул:

, (110)

В нижнем уравнении в (107) мы сменили систему наблюдения, на противоположную систему наблюдения с переходом кинетической энергии излучения в потенциальную энергию за счёт умножения левой части уравнения на с². При этом (при смене системы наблюдения на противоположную систему наблюдения) происходит смена направленного движения на замкнутое движение (иначе отличий между противоположностями нет) со сменой системы координат от длины и времени на две оставшиеся координаты длины в перпендикулярной плоскости. В этом случае волновое направленное излучение превращается в ротор. Это соответствует закону Био-Савара-Лапласа (97) с наличием тока с движением заряженной частицы со скоростью .

Напомним, что по теории Дирака значение единичного заряда (е) равно . Так как значение заряда не входит в уравнение энергии Эйнштейна, то может отражать только знак. Полученный результат в (107) соответствует нашей теории, где волновые свойства в одной противоположности преобразуются в корпускулярные свойства в другой противоположности. Таким образом, волновое уравнение, связанное с излучением или поглощением в одной противоположности, эквивалентно движению заряженной частицы (току) в другой противоположности с соблюдением закона Био-Савара-Лапласа (97). Это соответствует уравнению гармонического осциллятора (3). Ещё раз напомним то, что любое движение связано с излучением и поглощением, фактически ввёл Луи де Бройль. Таким образом, мы видим, что ошибки физиков, с переходом к чудесам телепортации за счёт вероятностей, были связаны не с тем, что не было каких-то уравнений в физике, а с тем, что они не смогли правильно связать в единую логическую цепочку то, что давно использовалось интуитивно в физике. Именно в этом наша заслуга.

Следует отметить, что мы лишь за счёт использования вида волновых функций, которые также уже использовались до нас, и соответствующих матриц для векторных потенциалов с учётом наличия противоположностей, убрали из конечного результата в (52) противоречия. Напомним, что эти противоречия были связаны с наличием членов e²A²Ψ (это не соответствовало взаимодействию от магнитной силы) и удвоением величины взаимодействия внешней магнитной силы с импульсом частицы в виде 2ec PA Ψ, так как для силы Лоренца (95) такого удвоения нет при воздействии на частицу.

В итоге величина взаимодействия PG в конечной формуле (89) для случая отражения движения электрона должна представляться в виде:

, (111)

В результате, с учётом того, что по нашей теории m₀=1/c=const, изменение энергии под влиянием магнитной силы определяется уравнением:

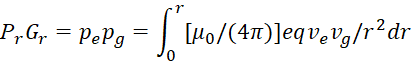, (112)

Здесь также аналогично варианту с электрической силой необходимо рассматривать вариант отдельного движения по трём координатам длины с использованием уравнений Гамильтона-Якоби по каждой из координат, так как иначе не будет зависимости от магнитной силы в силу того, что значения скорости при постоянном значении радиуса окружности орбиты электрона также не меняются. Понятно, что для случая движения заряда по стационарной орбите магнитная сила будет направлена противоположно электрической силе, и они компенсируют друг друга в динамике движения частицы.

Соответственно, необходимо указать практическое подтверждение использования электрической и магнитной силы при описании орбитального движения. С этой целью необходимо вспомнить формулу отношения магнитной силы к электрической на основании формул (91) и (96) при взаимодействии одинаковых точечных зарядов (e) в виде [17, с. 119]:

, (113)

Такое отношение для вращающегося электрона вокруг протона связано с тем, что мы имеем симметрию в противоположностях, которая обусловлена законом сохранения количества в противоположностях. При этом противоположные частицы в противоположностях имеют одинаковую скорость по отношению к абсолютной системе отсчёта, и если в одной системе наблюдения мы имеем электрон, то в противоположной системе наблюдения он будет интерпретироваться как антипротон, и наоборот. Иное исключает наличие противоположностей и симметрию с учётом закона сохранения количества в мироздании. Это значение в (113) должно определять отношение радиусов электрона и первой боровской орбиты в противоположной системе наблюдения. С этой целью необходимо иметь преобразование значения скорости в параметр длины среды распространения, аналогично тому, как поступил Бор. При этом соответственно используются значения констант электрической и магнитной проницаемости с учётом обратно-пропорциональной связи длины и скорости (последняя формула в (6)). Отсюда формулу (113) с учётом мы должны представить в виде:

, (114)

Здесь мы учитываем, что в отличие от системы СИ у нас отношение . Это связано с тем, что в системе СИ не учитывается различие констант электрической и магнитной проницаемости на скорость света как противоположностей по аналогии с длиной и временем. Это означает парадокс, так как отличие только количественное. Указанное нами не позволяет характеризовать пространственно-временное искривление среды по СТО и ОТО Эйнштейна. Кроме того, в данном случае длина с учётом последнего уравнения в (6) рассматривается как величина, соответствующая длине окружности. Поэтому, чтобы перейти к отношению радиусов мы должны учесть различие h² от на . При этом устойчивое состояние протона достигается за счёт максимума по спектру излучения, которое отличается от среднего значения в соответствии с формулой Планка [22, с. 31] на коэффициент 4,965. Отсюда отношение радиуса первой боровской орбиты r_бо к радиусу электрона r_э будет определяться в виде:

, (115)

В классике квантовой механики также проведены расчёты отношения радиуса первой боровской орбиты к радиусу электрона. При этом радиус электрона равен величие:

, (116)

Радиус первой боровской орбиты равен:

, (117)

В этом случае имеем:

, (118)

Кроме того, если сделать пересчёт при использовании постоянной тонкой структуры, то получим и . Их отношение даёт значение .

Иными словами, в классической квантовой механике получается практически аналогичный результат. Однако этот результат получен без учёта параметров среды распространения, таких как константы электрической и магнитной проницаемости, что говорит об отсутствии изменения самой среды и его применения как переносчика взаимодействия.

При этом значение заряда q = е = 1,602176487∙10^‒19 Кл противоречит уравнению энергии Эйнштейна, где под заряд нет энергии и . Следовательно, вычисление первой боровской орбиты на основе системы измерения СИ дало хорошие результаты в результате подгонки за счёт выбора соответствующих единиц измерения. В системе СГС константы электрической и магнитной проницаемости вообще равны единице.

Иными словами, среда распространения в системе единиц измерения, утверждёнными физиками, ‒ это некая «однородная» субстанция не подчиняющаяся СТО и ОТО Эйнштейна. Кроме того, введённые искусственно системы измерения СИ и СГС привели в итоге к обоснованию чёрных дыр из-за радиуса Шварцшильда, кварков и глюонов из-за дробности электрических зарядов, которые выражают энергию взаимодействия.

В результате имеем следующие выводы:

1. Изначальный подход использования в системе уравнений Дирака волновых функций, характеризующих вероятность, уже исключает методику подстановки одних функций через другие, так как вероятность связана с независимостью явлений. Поэтому, мы заменили волновые функции, характеризующие вероятность, на реальные электромагнитные функции. Именно на основе этих электромагнитных функций получается переход от простейших объектов ‒ электронных и мюонных нейтрино (антинейтрино), к корпускулярным и волновым свойствам всех остальных частиц;
2. Принцип перехода от системы уравнений Дирака к уравнению аналогичному уравнению Гамильтона-Якоби (уравнение Паули) должен был основываться на использовании влияния на частицу внешних независимых сил. Однако дифференциальный оператор 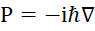в формуле (39), который при воздействии на волновую функцию характеризует импульс, вдруг стал воздействовать на внешний векторный потенциал е/сА с изменением при этом в напряжённость магнитного поля в виде Н=rot A. Это противоречит изначальному дифференциальному оператору, выражающему независимость этих величин в виде 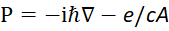. Иными словами, воздействие дифференциального оператора на внешнее магнитное поле, а также и электрическое поле в виде 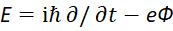, изначально не предусматривается. При этом, каким образом градиент вдруг превратился в ротор остаётся загадкой, так как при приведении подобных членов с противоположными знаками (как это мы показали выше) для этого нет причин;
3. Наличие внешнего векторного потенциала в виде еФ, также даёт парадокс, связанный с тем, что мы имеем выражение (31) вида E‒eФ=m₀v²/2, а это означает, что частица может иметь радиальную составляющую скорости от ядра атома. То есть, никакого удержания ядром электрона нет;
4. В системе уравнений Дирака отсутствует влияние среды распространения в виде констант электрической и магнитной проницаемости. Получается, что через среду невозможно оказывать воздействие в силу отсутствия её изменения под действием объектов. Парадокс и в том, что именно за счёт использования дробного значения величины заряда в системе измерения СГС и СИ получено совпадение с практикой отношения первой боровской орбиты к радиусу электрона, что противоречит уравнению энергии Эйнштейна, где заряд равен ;
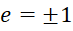5. Наличие парадоксов в вероятностной квантовой механике по системе уравнений Дирака означает необходимость нахождения такой математической модели движения электрона вокруг протона, которая не имела бы указанных парадоксов с учётом воздействия внешних сил. Поэтому, предлагаемый нами переход от системы уравнений Дирака к уравнению Гамильтона-Якоби основывается на известных законах и формулах, давно введённых в физику. Мы лишь связали их в единую логическую цепочку. При этом полученное нами теоретическое значение отношения первой боровской орбиты к радиусу электрона соответствует практическому результату без парадоксов предыдущих вычислений в квантовой механике;
6. Движение частицы по орбите связано с излучением, и это даёт парадокс падения электрона на ядро. Однако по нашей теории излучение в одной глобальной противоположности характеризуется как потенциальная энергия в другой глобальной противоположности, что определяется через константы электрической и магнитной проницаемости, что и даёт за счёт электрических и магнитных сил восполнение энергии движущейся частицы;
7. Излучение при движении частицы по орбите связано с постоянным воздействием от внешних электрических и магнитных сил. В этом случае, для описания такого движения, необходимо рассматривать изменение внешних электрических и магнитных сил относительно каждой из трёх координат длины на основе уравнений Гамильтона-Якоби;
8. В результате проведённых логических рассуждений, с учётом рассмотрения процессов от простого варианта к сложному варианту, мы показали последовательное использование формул физики и электродинамики для вычисления динамики детерминированного орбитального движения электрона вокруг протона на основе изначально известных электрических и магнитных сил, действующих на частицу.

Собственно иного варианта взаимодействия электромагнитных функций с иными силами, кроме как электрических и магнитных сил невозможно предположить. Понятно, что иной вариант приведёт только к чудесам телепортаций и возникновению неких виртуальных частиц и фотонов из вакуума. Можно, конечно, и дальше выдумывать новые частицы с кварками и глюонами, и придумывать для них странности, очарования и цвета, но дальнейшего продвижения физики, как науки, это не даст. Из стен университетов будут выходить умственно отсталые инженеры, которые не смогут на таком фундаменте продвигать далее науку, которая уже сейчас превратилась в новую религию.