Определение столкновений между объектами в видеоиграх

Введение

Видеоиграм приходится делить свое весьма ограниченное вычислительное время между несколькими задачами. Несмотря на ограничение ресурсов и использование относительно примитивных алгоритмов обнаружения столкновений, программистам удается создавать правдоподобные, хотя и неточные системы.

Долгое время в видеоиграх было очень ограниченное количество объектов для обработки, поэтому проверка всех столкновений не представляла проблемы. В двухмерных играх в некоторых случаях аппаратное обеспечение могло эффективно обнаруживать и сообщать о перекрывающихся пикселях между спрайтами на экране. В трехмерных играх часто используются методы пространственного разделения, а для проверки столкновений долгое время использовалась одна или несколько сфер на реальный 3D-объект. Точные проверки встречаются очень редко, только в играх, пытающихся точно имитировать реальность. Но, даже в этом случае точные проверки не обязательны.

Поскольку в играх не нужно имитировать реальную физику, стабильность не так важна. Почти во всех играх столкновения часто решаются с помощью очень простых правил. Например, если персонаж столкнулся с препятствием, его можно просто переместить обратно в последнее известное хорошее место. Некоторые игры рассчитывают расстояние, на которое персонаж может переместиться, прежде чем столкнётся с препятствием, и позволяют ему переместиться только на это расстояние.

Во многих случаях в видеоиграх для обнаружения столкновений с окружением достаточно аппроксимировать персонажей точкой. В этом случае двоичные деревья разбиения пространства (BSP) обеспечивают жизнеспособный, эффективный и простой алгоритм проверки того, пересекается ли точка с декорацией или нет.

Определение столкновений

При попытке определить произошло ли столкновение между двумя объектами, обычно используются данные вершин самих объектов, поскольку эти объекты часто имеют сложную форму; это, в свою очередь, усложняет обнаружение столкновений. По этой причине для обнаружения столкновений принято использовать более простые фигуры (которые обычно имеют хорошее математическое определение), их необходимо наложить поверх исходного объекта. Затем идёт проверка наличия столкновений на основе этих простых фигур; это упрощает код и значительно экономит производительность. В качестве примера можно привести: круги, сферы, прямоугольники и коробки; с ними гораздо проще работать, чем с произвольными сетками с сотнями треугольников.

Хотя простые формы дают нам более простые и эффективные алгоритмы обнаружения столкновений, их общим недостатком является то, что эти формы обычно не полностью окружают объект. В результате может быть обнаружено столкновение, у которого, на самом деле, не было соприкосновения с реальным объектом; следует всегда помнить, что эти фигуры являются лишь приближением к реальным фигурам.

Существует множество методов определения столкновений между объектами. Далее будет рассмотрено несколько основных способов.

AABB столкновения

AABB (Axis-Aligned Bounding Box) представляет собой прямоугольную фигуру столкновения, выровненную вдоль осей базиса сцены (для двумерного случая выравнивание происходит по осям x и y) (рис.1). Выравненность по оси означает, что прямоугольный бокс не вращается, а его края параллельны базовым осям сцены (например, левый и правый края параллельны оси y). Тот факт, что эти прямоугольники всегда выровнены по осям сцены, облегчает вычисления.

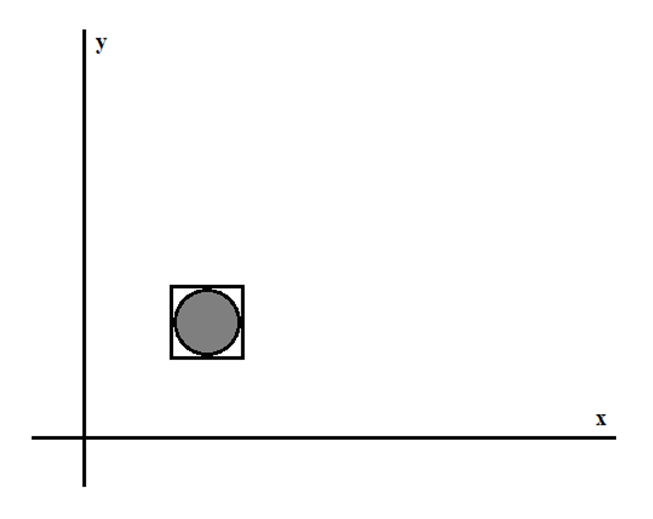
Рис. 1. Прямоугольная фигура столкновения

Столкновение происходит, когда две фигуры попадают в области друг друга, например, фигура, определяющая первый объект, каким-то образом оказывается внутри фигуры второго объекта (рис. 2). Для AABB это довольно легко определить благодаря тому, что они выровнены по осям сцены: нужно проверить для каждой оси, пересекаются ли края двух объектов на этой оси. Таким образом, мы проверяем, перекрываются ли горизонтальные и вертикальные края обоих объектов. Если и горизонтальные, и вертикальные грани пересекаются, происходит столкновение.

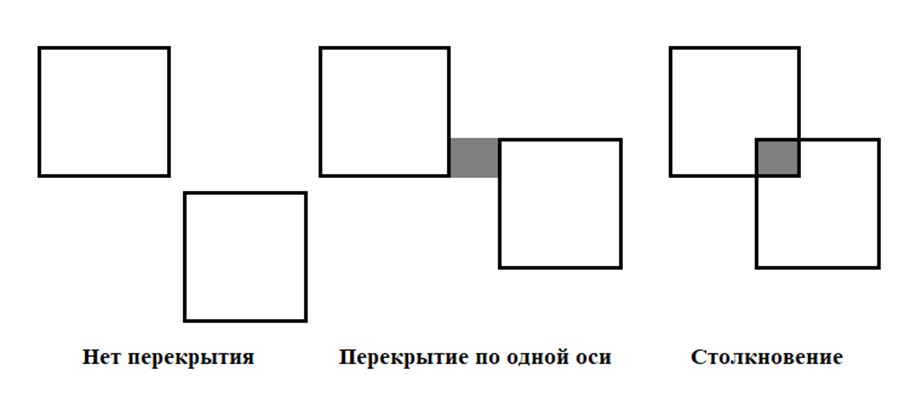
Рис. 2. Столкновение прямоугольников

Код этого метода относительно прост. Необходимо проверить перекрытие по обеим осям и, если это так, возвратить столкновение:

bool CheckCollision(GameObject &one, GameObject &two)

{

 bool collisionX = one.Position.x + one.Size.x >= two.Position.x && two.Position.x + two.Size.x >= one.Position.x;

 bool collisionY = one.Position.y + one.Size.y >= two.Position.y && two.Position.y + two.Size.y >= one.Position.y;

 return collisionX && collisionY;

}

Окружность и AABB

Обнаружение столкновений между окружностью и прямоугольником немного сложнее, он заключается в следующем: необходимо найти точку на AABB, которая находится ближе всего к кругу, и если расстояние от круга до этой точки меньше его радиуса, то столкновение произошло (рис. 3). Это означает, что придется обновить алгоритм обнаружения, поскольку в настоящее время он работает только между двумя AABB. Самое сложное – найти эту ближайшую точку на AABB.

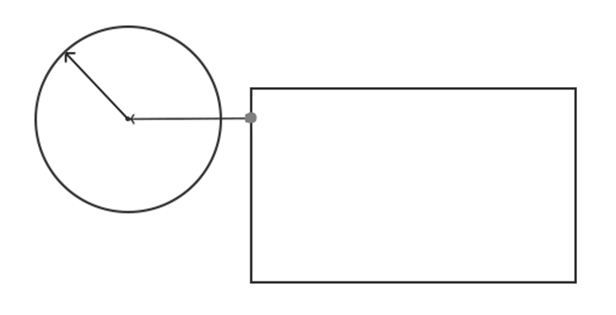
Рис. 3. Определение столкновения окружности и прямоугольника

Далее приведен код для определения столкновения между окружностью и прямоугольником:

bool CheckCollision(BallObject &one, GameObject &two)

{

 glm::vec2 center(one.Position + one.Radius);

 glm::vec2 aabb_half_extents(two.Size.x / 2.0f, two.Size.y / 2.0f);

 glm::vec2 aabb_center(

 two.Position.x + aabb_half_extents.x,

 two.Position.y + aabb_half_extents.y

 );

 glm::vec2 difference = center - aabb_center;

 glm::vec2 clamped = glm::clamp(difference, -aabb_half_extents, aabb_half_extents);

 glm::vec2 closest = aabb_center + clamped;

 difference = closest - center;

 return glm::length(difference) < one.Radius;

}

Столкновение двух окружностей

На данный момент определение столкновения двух окружностей между собой является самым простым и производительным алгоритмом. Метод подходит для простых игровых объектов или когда сложный объект описывается множеством окружностей. Столкновение основывается на вычислении расстояния между их центрами и сравнении этого расстояния с суммой их радиусов:

bool intersectSphere &sphere, Sphere &other)

{

 float dx = sphere.x - other.x;

 float dy = sphere.y - other.y;

 float dz = sphere.z - other.z;

 float distanceSquared = dx * dx + dy * dy + dz * dz;

 float radiusSum = sphere.radius + other.radius;

 return distanceSquared < (radiusSum * radiusSum);

}

Заключение

Определение столкновений является неотъемлемой частью разработки видеоигр, влияющей как на производительность, так и на качество игрового процесса. Правильный выбор алгоритмов и подходов к обнаружению столкновений, помогает поддерживать плавность игры и ее реалистичность. Разработчики должны находить баланс между точностью обнаружения столкновений и производительностью. Использование простых геометрических форм, таких как AABB и окружности, позволяет ускорить процесс, но может привести к ложным срабатываниям. Метод определения столкновений нужно выбирать тщательно в зависимости от целей игры. Аппроксимация сложных объектов простыми геометрическими фигурами, такими как прямоугольники и круги, значительно упрощает алгоритмы обнаружения столкновений и делает их более эффективными. Таким образом, понимание и применение различных подходов к обнаружению столкновений, является ключевым аспектом в разработке видеоигр, обеспечивающих высокое качество и производительность.