Развитие электродинамики и физики на основе теории мироздания. Часть 4. Подгонки под результат в квантовой механике и физике. Часть 9

В начале, следует отметить, что исходя из корпускулярно-волнового дуализма любого объекта, следует необходимость количественного равенства между глобальными противоположностями при обмене в формировании любого объекта Мироздания, если нет распада. Это означает равенство волнового уравнения Даламбера и корпускулярного уравнения Гамильтона-Якоби с точки зрения количественного преобразования и обмена между ними. Отсюда следует, что корпускулярное движение в одной противоположности представляется в электромагнитном виде напряжённостей полей в другой противоположности, и наоборот. Как нами было показано ранее в [1, с. 5-36; 2, с. 10-37; 3, с. 5-44] это вытекает из равенства электрических и магнитных полей в виде уравнения:

, (1)

При этом учитывалась динамика изменения векторных потенциалов в виде:

, (2)

Соответственно изменения векторных потенциалов связаны с движением корпускулярных частиц в противоположной системе наблюдения. Именно это и было применено Фейнманом [4, с. 273], но с ошибкой описания векторных потенциалов в той же системе наблюдения, что и электромагнитные составляющие с выводом наличия полей от значения, движущегося и неподвижного заряда, что также применяется и для электромагнитных составляющих. Это означает двойственность образования электромагнитных полей. С одной стороны, зависимость электромагнитных составляющих от заряда, за счёт значений по длине и времени, прямая, а для векторных потенциалов электромагнитные поля зависят от того же заряда, но с взятием производных от длины и времени. В итоге получается парадокс, при котором электрическое поле при изменении формирует само себя, что было показано нами в [3, с. 5-44]. Отсюда, суть разницы с нашей теорией в том, что в нашем случае результат образования электромагнитных составляющих в нашей системе наблюдения связан с обменным процессом от производных векторных потенциалов в противоположной системе наблюдения. Это достигается за счёт замкнутого движения частиц в виде ротора (по сути, это гармонический осциллятор), и прямолинейном движении частиц (если считать тангенциальную составляющую скорости), где обменный замкнутый процесс связан с преобразованием длины в проекцию на время в соответствии с СТО Эйнштейна, и наоборот. При этом наш подход позволил доказать симметрию представления электромагнитных процессов в противоположных системах наблюдения, при которых усовершенствованные уравнения Максвелла вида:

, (3)

Имеют аналогичный вид представления через векторные потенциалы:

, (4)

Здесь i=(‒1)^1/2, которая также впервые была введена не нами в уравнения Максвелла и использовалась для комплексных значений электрической и магнитной проницаемости, что мы показали в [1, с. 5-36]. Напомним, что сам принцип наличия противоположной системы наблюдения с преобразованием корпускулярных свойств в волновые свойства, и наоборот, был придуман не нами, а следовал из СТО и ОТО Эйнштейна, в силу того, что Эйнштейн в ОТО фактически ввёл для описания пространственно-временного искривления, для отражения значений скоростей, абсолютную систему отсчёта, связанную с нашей через скорость света. Понятно, что скорость, отражающая пространственно-временное искривление по ОТО Эйнштейна, не может представляться через значения по координатам осей в трёхмерном пространстве. Для такой скорости с учётом абсолютной системы отсчёта, связанной с нашей системой наблюдения через скорость света, отображение связано с проекцией на время. Только в этом случае будет выполняться как СТО, так и ОТО Эйнштейна. Понятно, что соответствие напряжённостей электромагнитных полей для подчинения СТО и ОТО Эйнштейна физики попытались связать по формуле, которая аналогична формуле связи длины и времени в виде:

, (5)

В итоге через векторные потенциалы получили выражение:

, (6)

Сравнивая нижнее уравнение (5) с уравнением (6), мы видим отличие (6) от нижнего уравнения (5) в том, что в уравнение (6) входит константа магнитной проницаемости , которая характеризует состояние среды распространения. Соответственно есть разница и на величину . Но эти отличия имеют объяснение. Так, константа магнитной проницаемости по ОТО Эйнштейна может характеризовать состояние среды только через пространственно-временное искривление, так как ничего другого и нет. Кроме того, по ОТО Эйнштейна это пространственно-временное искривление связано со значением скорости, которая отсчитывается от абсолютной системы отсчёта, связанной с нашей через скорость света. Поэтому, нам следует выразить константы магнитной и электрической проницаемости через усреднённое (интегральное) движение частиц, со скоростью (кинетической энергией) в противоположной системе наблюдения  , связанной с нашей системой наблюдения через скорость света в виде:

, (7)

Понятно, что константы электрической и магнитной проницаемости не могут иметь аналогичный вид, что исключает их представление как противоположностей, и поэтому они отличаются на значение с². Это не соответствует представлению этих констант в системе измерения СИ, где константы отличаются только количественно, так как их отношение это число, и они не отражают противоположности. При этом мы видим, что константы электрической и магнитной проницаемости имеют обратно-пропорциональную связь. Подход выбора усреднённого значения скорости в противоположности связан с тем, что это значение определяет условие термодинамического равновесия по формуле Планка, что определяет стабильность частиц в динамике обмена с окружающей средой. Совпадение по преобразованию нижнего уравнения (5) с (6) можно получить, если исходить из того, что при соблюдении того же закона преобразования составляющие не могут иметь один и то же вид при смене системы наблюдения. При связи противоположных систем наблюдения через скорость света электромагнитные компоненты меняются местами. Отсюда при смене электромагнитных компонент за счёт смены системы наблюдения будем иметь связь . При равенстве замкнутых преобразований для стабильного объекта имеем, что v=v_пр. В этом случае значение Е отражает в нижнем уравнении величину времени (5), а Н величину длины. Иными словами, связь электромагнитных составляющих по (6) отражает соблюдение СТО и ОТО Эйнштейна в более общем случае взаимодействия. Отсюда можно сделать следующие преобразования формулы (6):

, (8)

Последнее уравнение в (8) соответствует замкнутой системе двух противоположностей по уравнению окружности с учётом обратно-пропорциональной связи. Собственно, при условии сохранения объекта, динамика взаимодействия противоположных частей объекта, с учётом наблюдения из одной выбранной противоположности, будет выглядеть в нормированном к максимальной скорости обмена виде:

, (9)

Перепишем полученное уравнение в ином виде:

, (10)

Далее произведем следующие преобразования:

, (11)

Последнее уравнение по виду аналогично уравнению преобразований Лоренца. И отсюда мы также можем получить соответствие с уравнением энергии Эйнштейна, если сделать замену переменных и считать, что m=1/v₁, а m₀=1/c. В итоге имеем:

, (12)

Если умножить оба члена указанного последнего уравнения на одинаковую величину c²=с/h=N, то получим формулу энергии Эйнштейна в виде . Значение N определяет общее количество элементарных объектов в мироздании при обмене при их взаимосвязи через скорость света. Как мы видим, ограничение количества элементарных объектов в мироздании определяется константами в скорость света и постоянной Планка. Иного и быть не может в силу того, что изменение количества объектов в мироздании означает отсутствие замкнутости мироздания с наличием чудес исчезновения объектов и их возникновения из нуля. Соответственно мы видим, что энергия и масса выступают как противоположности, связанные обратно-пропорциональной связью, и фактически они заменяют соотношение неопределённостей Гейзенберга в детерминированном виде. Можно представить энергию Эйнштейна и в ином виде:

, (13)

Это означает, что из преобразований Лоренца, которые тоже связаны с формулой окружности, получается и уравнение энергии Эйнштейна. Учитывая, что в формулу Эйнштейна входят только две переменные величины, которые дают замкнутую систему по формуле окружности, то они и являются противоположностями друг для друга (аналогично длине и времени, которые связаны через скорость света, что было впервые сделано Минковским в [5, с. 226]), т. е. могут преобразовываться только друг в друга. А отсюда следует, что указанные величины не могут выражаться через один и тот же вид. Иначе такое преобразование ничем не зафиксировать в силу отсутствия различий между противоположностями. Однозначная связь скорости света и величины постоянной Планка в виде ch=1, с учётом необходимости смены представления объектов в противоположных системах наблюдения, означает необходимость записи m₀=h=1/с. Аналогичный вариант был предложен интуитивно физиками в системе измерения СИ в виде постоянной тонкой структуры . Однако, при этом нарушается необходимость взаимодействия с охватом всех частиц мироздания через значение скорости обмена (скорости света). Здесь, мы элементарную минимальную массу объекта представляем в виде величины, связанной с величиной постоянной Планка, так как мироздание оперирует в реальности количеством в виде объектов минимальной величины и закономерностями. То есть Мироздание ничего не знает о системах измерения массы (например, в килограммах), придуманных людьми. Отметим, что системы измерения, придуманные людьми, приводят к парадоксам в виде чёрных дыр (система измерения СИ) и обоснования вакуума как пустоты, подчинённой геометрии Эвклида (система измерения СГС, где в классических уравнениях Максвелла исключаются константы электрической и магнитной проницаемости для характеристики пространства и времени как объектов). Выбор дискретной величины для массы покоя равной постоянной Планка означает, что электрон и позитрон – это минимальные дискретные корпускулярные объекты, и их изменение связано только с переходом в противоположность в результате аннигиляции, а не распада на ещё более мелкие корпускулярные объекты. Соответственно в системе мироздания, если одна переменная величина выражает скорость v, то второй изменяемой переменной остаётся роль массы и при этом v₁=1/m. В противном случае определить наличие противоположностей невозможно, если вид объектов в противоположностях сохраняется. Так как операция сложения при инвариантной форме, за счёт переноса значения v², из левой части уравнения (9) от знака равенства в правую часть от знака равенства в (10), приводит к смене суммы на разность, то для соблюдения инвариантной формы в виде тождества необходимо сменить и закономерности. Другими словами, мы переходим из рассмотрения процесса в волновом виде к корпускулярному виду, и сложение в одной противоположности должно отображаться вычитанием в другой противоположности. Именно преобразования СТО требуют наличия разных систем наблюдения от длины и времени. Для показа этого мы сделаем следующие преобразования СТО Эйнштейна в замкнутом виде [6, с. 213]:

, (14)

Здесь , в этом случае аргументы имеют равенство по количеству.

И такая связь не наша выдумка, и была введена в квантовую механику в виде равенства x=ict [7, с. 317-318]; отличие лишь в том, что интуитивный подход физиков в нашей теории означает связь противоположностей и обеспечивает смену закономерностей, а значит и вида объектов Мироздания, при смене системы наблюдения на противоположную систему. Таким образом, мы фактически имеем подтверждение общей формулы Мироздания, которая была выведена нами в [8, с. 5-37] на основании СТО Эйнштейна, когда полная замкнутость действительна для варианта всего Мироздания с учётом v=c. Следовательно, если бы закономерности сохранялись при переходе, то уравнять сложение и вычитание, что характеризует обмен, было бы невозможно. То есть в физике, в отличие от математики, нельзя произвольно переставлять переменные интегрирования или дифференцирования в силу того, что изменение означает новый объект воздействия и исключает цикл Карно с наличием возможности вечного двигателя. Одновременно надо учитывать и смену знаков при переносе членов из одной части равенства в другую часть. Это позволяет сохранить тождество при инвариантной форме. То есть с этим переносом надо учесть и изменение представления с учётом смены места наблюдения. Надо отметить, что смену систему наблюдения с учётом обратно-пропорциональной связи впервые также фактически ввели не мы, а Бор. При этом он использовал уравнение гармонического осциллятора, которое (при нормировке) отражает уравнение окружности в виде [9, с. 58-59].

, (15)

Суть необходимости использования уравнения гармонического осциллятора для объяснения взаимодействия противоположностей с наличием частоты излучения мы покажем несколько ниже. Из (15) Бор получил формулы вида:

, (16)

При определении первой орбиты водорода он фактически использовал смену системы наблюдения за счёт формулы при замене импульса на радиус орбиты, и получил уравнение:

, (17)

Однако парадокс, допущенный Бором в том, что своим постулатом он исключил излучение при движении электрона на дискретных орбитах, в то время как уравнение гармонического осциллятора именно основано на излучении, в виде значения .

Отметим, что с учётом нашей теории разница на , не позволяет представить длину и скорость как противоположности с учётом условия охвата всех объектов Мироздания при взаимодействии. Величина радиуса характеризует систему наблюдение процесса, но не определяет взаимодействие в преобразовании величин. Отсюда правильная нормировка в динамике взаимодействия соответствует не радиусу, а длине окружности, по которой осуществляется взаимодействие с учётом формул:

, (18)

В результате изменения по скорости и длине с учётом систем наблюдения и обратно-пропорциональной связи равны. Отсюда никаких нормировочных коэффициентов в этом случае не требуется. Следует отметить, что, так как в среде распространения значение длины окружности отражается через пространственно-временное искривление, так как в противном случае мы имеем геометрию Эвклида без возможности связи по координатам, то в противоположной системе наблюдения это значение играет роль массы, и мы можем записать r=m=1/v. Это означает, что скорость в одной системе наблюдения представляется значением массы в противоположной системе наблюдения. Иное исключает противоположности и корпускулярно-волновой дуализм. Следовательно, мы расширили замену, введённую Бором исходя из того, что массы как таковой вне описания пространственно-временного искривления по СТО и ОТО Эйнштейна не существует. В современной физике сейчас господствует представление, что масса это нечто отдельное и отсюда возможна некая нейтральная масса внутри пространственно-временного искривления среды распространения. При этом придумано даже отдельное взаимодействие через гравитоны. О парадоксах, которые при этом имеют место, мы говорили в [3, с. 5-44].

Далее необходимо вспомнить саму формулу Луи де Бройля [10, с. 63]:

, (19)

Как мы не раз показывали, эта формула выводится из аргумента волновой функции , которая отражает условие, где количественные изменения в противоположностях равны:

, (20)

С учётом нашей теории для элементарной частицы с массой m₀=1/c мы можем связать частоту и скорость в виде:

, (21)

Здесь необходимо отметить, что представление через частоту и скорость относится к противоположным системам наблюдения, связанным через скорость света. Иными словами, мы имеем первоначальную связь через скорость света аналогично связи длины и времени по идее Минковского [5, с. 226]. Из формулы (21) также следует, что представление процесса и физических величин также зависит от системы наблюдения. Теперь вспомним известную формулу Луи де Бройля для описания «волн материи» по которой со всякой неподвижной частицей массой m связан некоторый периодический процесс частоты f [11, с. 216] и учтём ОТО Эйнштейна, а также что по нашей теории m₀=1/c=h:

, (22)

Соответственно, мы видим полное совпадение с нижней формулой (8), которая была выведена из связи электрических и магнитных составляющих. Это как раз подтверждает логику нашей теории, по которой движение в одной системе наблюдения отображается через электромагнитные составляющие в другой противоположной системе наблюдения, так как мы имеем общий закон преобразования. Отсюда, как раз и следует вывод о том, что некие «волны материи», которые придумал Луи де Бройль, отражают электромагнитные волны, но в противоположной системе наблюдения. Иными словами, корпускулярное движение в одной системе наблюдения отображается в виде электромагнитных составляющих в противоположной системе наблюдения, связанной с первой системой через скорость света без чудес волновых функций, характеризующих вероятность.

Таким образом, мы видим, что сами математические подходы с подчинением СТО и ОТО Эйнштейна по описанию возникновения электромагнитных составляющих за счёт движения были сделаны и до нас физиками, однако, они не учли сам принцип формирования этих составляющих связанный с преобразованием и обменным процессом между противоположностями с учётом противоположных систем наблюдения и наличием обратно-пропорциональной связи. При этом физикам не хватило логики мышления, чтобы сделать правильные выводы из теории и практики, хотя все необходимые для этого формулы и предпосылки были.

Отсюда, в продолжении развития электродинамики и физики на основе нашей теории нам необходимо показать каким образом получается собственный магнитный момент для частиц с учётом перехода от волновых свойств к корпускулярным свойствам, и наоборот. Детально переход от волновых электромагнитных свойств к корпускулярным свойствам был нами показан в [1, с. 5-36; 2, с. 10-37; 3, с. 5-44]. Сейчас мы рассмотрим этот переход с целью выявления магнитных моментов с исключением парадоксов, которые были допущены физиками.

Непосредственная связь ротора стороннего тока в одной противоположности с формированием волнового процесса в другой противоположности, была фактически показана физиками в [12, с. 117]:

, (23)

Сам вывод этого уравнения физики сделали без понимания, что собой представляет этот сторонний ток, и тем более они ничего не знали о наличии противоположностей с существованием разных систем наблюдения. Одновременно физики вывели волновые равенства в комплексном виде на основе векторных потенциалов и с взятием производной по времени в [13, с. 40]

, (24)

Уравнения в (24) фактически отражают формирование волновых процессов на основе источников излучения, которые формируются за счёт изменения (преобразования) сторонних электрических и магнитных токов. Понятно, что преобразование нечто нереального невозможно и отсюда уже должен был следовать вывод, что если данные токи не наблюдаются в нашей системе наблюдения, то должна быть противоположная иная система наблюдения, где эти сторонние токи должны иметь реальное воплощение через движение реальных частиц. Иначе чуда не избежать. Собственно такой вывод уже следовал из СТО и ОТО Эйнштейна, где время не наблюдаемая в пространстве величина превращалась в эквивалент длины в зависимости от скорости, и наоборот.

При этом известно уравнение Даламбера на основе электрического стороннего тока с наличием волнового представления векторных потенциалов в виде [14, с. 119]:

, (25)

Это означает, что волновой электромагнитный процесс в противоположной системе наблюдения определяется процессом пространственно-временного искривления среды распространения уже в нашей системе наблюдения на основе стороннего электрического тока. Здесь также используется калибровка Лоренца вида . При этом мы имеем . Это означает, что смена системы наблюдения, о чём говорит смена переменных дифференцирования, приводит к тому, что компенсация в одной системе наблюдения означает сумму в другой системе наблюдения. При связи сА=Ф, аналогично первоначальной связи по длине и времени (r=ct, по идее Минковского [5, с. 226]) и переходе к единому отображению переменных в одинаковых величинах имеем и . Иными словами, то что является разностью от системы наблюдения от А, является суммой от системы наблюдения от Ф.

Если исходить из (23) и первых двух уравнений в (24), то отсюда следует запись равенства уже для магнитного поля в нашей системе наблюдения от ротора электрического стороннего тока в виде:

, (26)

Данная запись была также представлена, но для реального тока на основе формулы Био-Савара-Лапласа с определением значений тока в пространстве на основе корпускулярного движения частицы, и это, казалось бы, означает практическое подтверждение. Однако сторонний электрический ток – это не реальный ток в нашей системе пространства. При этом мы видим противоречие с последним уравнением в (24) где есть зависимость не только от электрического стороннего тока, но и от магнитного стороннего тока. Это означает, что запись (26) не является полной.

Чтобы это доказать, мы отметим, что помимо (23) и (24) физиками была выведена связь волновых процессов на основе векторных потенциалов со сторонними электрическими и магнитными токами. При этом согласно [1, с. 5-36; 3, с. 5-44] для варианта магнитного стороннего тока электрические и магнитные поля меняются местами, то есть мы имеем иную систему наблюдения (аналогично и для векторных потенциалов). Это также было замечено физиками в [15, с. 36] и магнитный сторонний ток впервые ввели не мы. Отсюда был определён векторный потенциал для напряжённости электрического поля вида:

, (27)

Одновременно для напряжённости магнитного поля по аналогии должен быть вид:

, (28)

Далее, исходя из уравнения вида , имеем:

, (29)

Отсюда мы имеем зависимость между сторонними электрическими и магнитными токами вида:

, (30)

Это означает, что мы имеем обратно-пропорциональную зависимость между сторонними электрическими и магнитными токами, которая совпадает с обратно-пропорциональной зависимостью для объектов длины и времени по СТО Эйнштейна с соблюдением инвариантности. По сути дела, исходя из значений констант электрической и магнитной проницаемости мы получаем, что в уравнениях волны через векторные потенциалы А и А^м отображаются значения электрической и магнитной индукции в соответствующей системе наблюдения. При этом сторонние электрические и магнитные токи отражают иное представление, чем в системе наблюдения по уравнениям (24), и они фактически отображают значения М^э и М^м, что означает смену системы наблюдения. Однако отметим вид уравнений (30) не может дать равенства в силу того, что слева от знака равенства присутствует волновая функция, а справа от знака равенства она отсутствует. Это несоответствие было исправлено Шредингером, который ввёл в квантовой механике умножение на волновую функцию Ψ в [16, с. 30-31] для обеих частей равенства:

, (31)

Собственно такое изменение имеет объяснение на основе нашей теории, где в уравнениях Максвелла сторонние токи имеют вид производных от волновых функций в виде [1, с. 5-36]:

, (32)

В итоге с учётом смены системы наблюдения на противоположную систему, с учётом того, что масса и скорость в противоположностях меняются местами (это фактически ввёл Бор с учётом обратно-пропорциональной связи), при имеем вид уравнений:

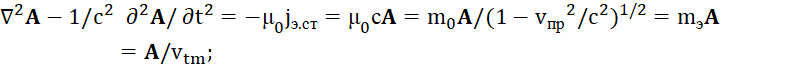
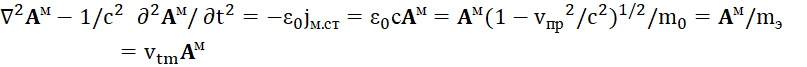, (33)

Таким образом, если для формирования магнитного или электрического волнового процесса в нашей системе наблюдения требовалась динамика изменения электрических и магнитных сторонних токов, то в противоположной системе наблюдения уже сам сторонний электрический или магнитный ток выступает источником формирования волновых процессов в противоположности. Иными словами, в одной системе наблюдения сторонние токи в динамике своего изменения (преобразования) формируют источник возбуждения волновых свойств, а в другой системе наблюдения уже сами являются источниками возбуждения волновых процессов. Однако в (33) мы имеем представление векторных потенциалов через первоначальную связь противоположностей через скорость света вида: , при этом волновые процессы в противоположности определяются состоянием среды распространения без корпускулярного движения частиц. Поэтому, для случая реального отображения этих векторных потенциалов в пространстве и времени в нашей системе наблюдения через корпускулярное движение частиц мы должны иметь их реальное преобразование в соответствии с СТО и ОТО Эйнштейна в зависимости от скорости в нашей системе наблюдения. Иное представление только в виде электромагнитных волн исключает обмен через излучение и поглощение из-за ассоциативного сложения и вычитания. Такое преобразование по аналогии с электромагнитными составляющими в (8) было также введено физиками на основе известной формулы связи векторных потенциалов из электродинамики [17, с. 165]:

, (34)

Отсюда при переходе в систему наблюдения от векторного потенциала А^м имеем для верхнего уравнения (33):

, (35)

Следовательно, если в случае отображения от системы наблюдения от векторного потенциала А мы имели зависимость формирования волнового процесса от константы магнитной проницаемости, выраженной через неподвижное пространственно-временное искривление в виде массы , то при отображении через векторный потенциал А^м, мы имеем представление от системы, связанной с наблюдением от времени, в которой масса движется со скоростью . Для нижнего уравнения в (33) мы должны учесть, что масса и скорость в противоположностях в соответствии с (18) и (33) меняются местами и в этом случае мы имеем уравнение (34) в виде:

, (36)

Отсюда имеем:

, (37)

Таким образом, мы видим, что волновой процесс в одной системе наблюдения формируется за счёт корпускулярного движения в системах противоположных данной системе волнового процесса с переходом массы в скорость, и наоборот. В одном случае смена системы наблюдения происходит за счёт умножения на скорость света как в уравнении (35), а в другом случае как в уравнении (37) в систему наблюдения за счёт деления на скорость света с учётом изменения уровня представления по иерархии в мироздании. Фактически мы имеем закон, по которому движущийся электрон в одной системе наблюдения представляется протоном в другой системе наблюдения. И данные представления частиц определяются на основе составляющих электромагнитной волны в соответствующей системе наблюдения.

Это как раз и говорит о том, что представление одного и того же объекта зависит от системы наблюдения и этот вывод, кстати, следовал по логике из уравнений, полученных самими физиками. Наша заслуга лишь в том, что мы учли, что в соответствии с СТО и ОТО Эйнштейна, с учётом связи противоположностей через скорость света, проекция на время переходит в проекцию длины, и наоборот, а это уже означает отображение в реальном виде в пространстве. Иными словами, то, что в одной системе наблюдения представляется в виде неподвижных объектов длины и времени с отображением через электрические и магнитные сторонние токи в виде пространственно-временного континуума через константы электрической и магнитной проницаемости, в противоположной системе наблюдения выглядит в качестве движущихся объектов длины и времени (противоположные заряды). Понятно, что сохранение вида в обеих системах наблюдения исключает преобразование с наличием самих противоположностей. Заметим, что отказ физиков от наличия иной системы наблюдения привёл к объяснению аномальных магнитных моментов через чудеса виртуальных кварков. При этом, как мы показали в [1, с. 5-36], волновые свойства для напряжённостей электрических и магнитных полей получаются также и в результате подстановки усовершенствованных уравнений Максвелла (электронные и мюонные нейтрино и антинейтрино) друг в друга, то есть всё определяется составляющими при взаимодействии. Ранее в (25) и в (29) рассматривалось взаимодействие через подстановку векторных потенциалов в уравнения Максвелла. При этом волновые уравнения связаны с производными по пространству и времени сторонних магнитных и электрических токов. То есть, для волновых электромагнитных процессов в нашей системе наблюдения были получены уравнения в [1, с. 5-36]:

, (38)

Иными словами, уже по уравнениям (24) и (38) следует ошибочность вывода волнового уравнения (23) в результате исключения симметрии процессов в противоположностях.

Собственно, необходимость формирования источников возбуждения электромагнитных полей от двух противоположностей, физиками в классической электродинамике была также предложена в виде записи через векторные потенциалы. Здесь источники возбуждения представляются в виде сумм [18, с. 39]:

, (39)

Анализируя уравнения (24), (38) и (39), мы видим, что вид волновых уравнений (38) и (39), в левой части от знака равенства совпадает. Отличие между сторонними токами и векторными потенциалами касается лишь знаков сложения и вычитания, что может означать смену системы наблюдения на противоположную систему. Отсюда, в соответствии с необходимостью симметрии между противоположностями для соблюдения закона сохранения количества, а также учитывая идентичность формул для векторных потенциалов и электромагнитных составляющих, что мы показали в [1, с. 5-36], можно сделать и обратную подстановку электромагнитных составляющих в векторные потенциалы. В результате по аналогии мы получим:

, (40)

Это аналогично виду для векторных потенциалов (33), что говорит о симметрии законов в противоположностях. Следовательно, мы видим, что все необходимые соотношения и формулы уже были получены в классической электродинамике, оставалось лишь логически связать эти соотношения с учётом нашей теории мироздания. При этом стабильная электромагнитная волна (фотон) рассматривается как замкнутая система, и для обеспечения её состояния как целого объекта мы имеем её представление в противоположности в корпускулярном виде как систему вращения электрона вокруг протона [3, с. 5-44]. Ещё раз подчеркнём, что волновые свойства в одной противоположности должны выражаться через корпускулярные свойства в другой противоположности, так как иначе различий нет. Собственно иное представление в противоположности в виде взаимодействия электрона и позитрона, не даст устойчивого состояния электромагнитной волны в нашей системе наблюдения, так, как если бы электромагнитная волна в противоположной системе наблюдения представлялась бы в виде частиц электрона и позитрона, то в этом случае была бы аннигиляция. Тогда корпускулярные свойства в разных системах наблюдения не могли в принципе возникнуть и во всех системах мы имели бы только волновое представление, что отрицает корпускулярно-волновой дуализм. Поэтому электрон в противоположной системе наблюдения представляется протоном с переходом кинетической энергии орбитального движения в дополнительную массу, что и следует из уравнений (35) и (37).

Следует отметить, что уравнения (33) с учётом отображения одинакового волнового вида при отражают закон связи силы Кулона и силы Лоренца, если учесть их взаимодействия через вычитание, как противоположностей в виде:

, (41)

Здесь была учтена связь противоположностей через значение с², которое аналогично связи Е=mc². В результате имеем аналогию связи силы Кулона с силой Лоренца при относительности электрических и магнитных полей [19, с. 274] в виде:

, (42)

Здесь, , и . Отличие в точке рассмотрения среды распространения от противоположной системы наблюдения связано со значением , так как константа электрической проницаемости уже связано со скоростью в противоположности. При этом, в силу того что в противоположности сила Кулона и сила Лоренца рассматриваются как результат констант электрической и магнитной проницаемости среды распространения, то в конкретной точке формирования этих сил значение отсутствует и этот член равен единице. Далее мы учтём, что по нашей теории f=cv=cu в (21),h=m₀=1/c. Отсюда получаем:

, (43)

Учитывая формулу гармонического осциллятора (15), при верхнем уравнении в (16) мы должны считать . При этом . Иными словами, взаимодействие сил, выраженное через напряжённости электрических и магнитных полей, связано с подчинением уравнению гармонического осциллятора. Поэтому нам надо обосновать причину такой связи исходя из условия замкнутого взаимодействия сил по уравнению Гамильтона-Якоби при наличии стабильного объекта Мироздания. По сути, это означает, что движение связано с излучением. С этой целью напомним, что гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы F=‒kx [20, с. 90]. Потенциальная энергия такой частицы имеет вид:

, (43)

Собственная частота классического гармонического осциллятора при массе частицы m₀ равна:

, (44)

Отсюда получим формулу для потенциальной энергии частицы в виде:

, (45)

Далее вспомним вывод уравнения Гамильтона-Якоби, которое при наличии силы F можно рассматривать как прямое следствие известного закона Ньютона:

F=ma=md²s/dt²= mdv/dt;

E=∫Fds=∫Fvdt=∫mvdv=mv²/2=p²/(2m), (46)

На следующем этапе по классической физике берётся некая функция действия с учётом равенств и . В результате имеем уравнение Гамильтона-Якоби без внешнего поля:

, (47)

С учётом внешнего поля уравнение Гамильтона-Якоби приобретает вид:

, (48)

После взятия производных мы имеем вид:

, (49)

Понятно, что движение с ускорением связано с излучением, одновременно для получения стабильного объекта необходимо и поглощение, что было замечено Эйнштейном для описания фотоэффекта в его уравнении вида [21, с. 36]:

, (50)

Отсюда с учётом равенства поглощения и излучения для наличия соблюдения закона сохранения количества между противоположностями при Е=hf получаем формулу гармонического осциллятора в виде (15). Однако далее необходимо обосновать замену потенциальной энергии на кинетическую энергию , и наоборот. Собственно такую замену мы обосновали в [2, с. 10-37]. Здесь мы только повторим данное доказательство, на основании которого Бор фактически получил значение первой боровской орбиты исходя из уравнения в (16) вида . Для этого более детально рассмотрим используемое в квантовой механике уравнение Шредингера, которое фактически связывает корпускулярные свойства с волновыми свойствами с учётом закона сохранения количества. При этом мы учитываем, что уравнение Шредингера с учётом внешних сил будет иметь вид [16, с. 30-31]:

, (51)

Собственно Шредингер попытался объединить чисто корпускулярное уравнение Гамильтона-Якоби на основе второго закона Ньютона с сочетанием при этом волновых свойств и внешнего воздействия U. Для этого он использовал нормировку на постоянную Планка и умножение первой производной от функции по времени на мнимую единицу. Соответственно, возведение в квадрат первой производной от функции по длине он заменил интуитивно двойным дифференцированием этой функции. В итоге волновой вид комплексной функции позволил получить решение аналогичное тому, какое следовало для уравнения Гамильтона-Якоби от второго закона Ньютона. Собственно совпадение решения для волновой функции с решением для функции для корпускулярной частицы означает возможность сочетания корпускулярных и волновых свойств в одном общем объекте. Но вид уравнений при этом оказался отличающимся. Тогда физики посчитали, что данное уравнение Шредингера должно удовлетворять условию, при котором оно должно в предельном случае переходить в уравнение Гамильтона-Якоби. С этой целью вместо волновой функции вводят функцию S при помощи соотношения [16, с. 30-31]:

, (52)

Далее учитывают равенства:


, (53)

Так как волновая функция Ψ входит во все члены лишь множителем, то её можно сократить, тогда получим:

, (54)

В предельном случае физики полагают, что при величине , данное уравнение переходит в уравнение Гамильтона-Якоби. Однако надо напомнить, что , а это означает, что перехода к уравнению Гамильтона-Якоби просто быть не может, так как нет варианта, при котором . А с учётом обратно-пропорциональной связи со скоростью света законов физики как таковых просто быть не может. То есть, при , получается однородность, нарушаются законы физики и, соответственно нет и самих противоположностей. Кроме того, в дальнейшем это уравнение (54) используется при методе Вентцеля-Крамерса-Бриллоэна (метод ВКБ) [22, с. 60] для сшивания функций на границе раздела с получением в конечном итоге правила квантования Бора-Зоммерфельда, на основании чего оправдывался туннельный эффект с прохождением через потенциальный энергетический барьер, а также наличие нулевой энергии по соотношению неопределённостей Гейзенберга. При этом исчезновение члена с величиной постоянной Планка исключало доказательство всех остальных преобразований. Парадоксы таких решений мы также подробно рассмотрели в [23, с. 5-27].

Понятно, что перехода к уравнению Гамильтона-Якоби от уравнения Шредингера в принципе быть не могло, так как это бы давало бы одинаковый результат при наличии разного взаимодействия, что означает двузначность законов физики.

Однако попытаемся понять, есть ли возможность перехода от уравнения Шредингера с волновой функцией Ψ к корпускулярному движению частицы, как это получилось для системы уравнений Дирака [24, с. 295]. Повторим, что суть отличия уравнения Шредингера от уравнения Гамильтона-Якоби, в том, что Шредингер ввёл двойное дифференцирование функции по длине, вместо возведения в квадрат значения первой производной от функции как в уравнении Гамильтона-Якоби (47). В этом случае с учётом того, что при взаимодействии через обмен (это выражается в изменениях) участвуют обе противоположности, которые в данном случае выражены через значения аргумента и функции, возведение в квадрат, как это показано, происходит на основании правил дифференцирования в математике с учётом закона сохранения количества. Таким образом, мы видим, что нормировочный коэффициент , в аргументе функции Ψ был необходим физикам для обоснования подгонки под результат перехода от уравнения Шредингера к уравнению Гамильтона-Якоби. Однако мы учитываем, что постоянная Планка ‒ это просто нормировочный коэффициент и его можно не учитывать, если рассматривать волновую функцию вида:

, (55)

Именно такой вид функции мы использовали при переходе от волновых свойств электромагнитных функций к корпускулярным свойствам на основании усовершенствованных уравнений Максвелла в [1, с. 5-36]. Однако отметим, что Дирак изменил правило дифференцирования при переходе от волновых свойств к корпускулярным свойствам при выводе своей системы уравнений [24, с. 295] в виде:

, (56)

Мы лишь аналогично убираем нормировку на величину постоянной Планка (), что следует при переходе от волновых функций Ψ, характеризующих вероятность, к реальным электромагнитным волновым функциям (55). Собственно постоянная Планка в результирующем уравнении в преобразованиях от системы Дирака также всё равно сокращается. Отсюда уравнение Шредингера с наличием замены на электромагнитные функции соответствует уравнению Гамильтона-Якоби без учёта внешних сил:

, (57)

Иными словами, волновая функция Ψ по (55) соответствует решению уравнения Гамильтона-Якоби, без добавочного умножения первой производной по времени на мнимую единицу, если учесть введённое Дираком правило (56), без которого переход от волновых свойств к корпускулярным свойствам был бы невозможен. Собственно, по логике нашей теории операции дифференцирования (интегрирования) также связаны с умножением на мнимую единицу [8, с. 5-37]. В противном случае не будет перехода от волнового вида к корпускулярному виду, и, наоборот, из-за отсутствия смены закономерностей и в силу того, что сложение в одной противоположности означает вычитание в другой противоположности. Повторяем ещё раз для оппонентов, что умножение на мнимую единицу при дифференцировании не наша выдумка, и было впервые применено интуитивно Дираком. Следует заметить, что добавочное дифференциальное изменение в уравнении Шредингера фактически означает, что это изменение даёт переход от функции, характеризующей корпускулярные свойства, к волновой электромагнитной функции. Более того отметим что нормировка аргумента волновой функции на в виде 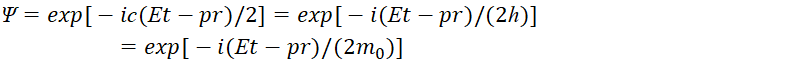позволяет совместить волновые и корпускулярные свойства через уравнение с учётом того, что в нашей теории h=m₀=1/с. Иными словами, изменение в одной противоположности, что выражается изменением по времени, в противоположности выражается изменением по длине. И обратная реакция даёт противодействие первоначальному изменению через двойное дифференцирование. Понятно, что данный результат, совмещения волновых и корпускулярных свойств, получить на основе отсутствия связи массы с пространственно-временным искривлением, помимо нашей теории, было невозможно. То есть корпускулярным свойствам, на основе уравнения Гамильтона-Якоби, соответствуют изменения волновых свойств на основе волновой функции вида с соблюдением закона противодействия на действие в виде . Деление на 2 в аргументе функции позволяет обеспечить переход к уравнению Гамильтона-Якоби с учётом перехода от уравнения силы F=ma. Как будет показано несколько ниже значение 1/(2m₀) соответствует гиромагнитному соотношению (), что используется при вычислении аномальных магнитных моментов. Иными словами, член 1/(2m₀) в аргументе функции характеризует коэффициент перехода от волновых свойств к корпускулярным свойствам. Отличие на величину с заменой на постоянную Планка h вместо , связано с тем, что в качестве системы наблюдения от длины рассматривается замкнутое движение частицы, с наличием силового воздействия и изменения по длине окружности. При системе наблюдения, связанной с радиусом, мы не можем иметь процессов изменений, так как радиус не изменяемая величина, отсюда никакой работы, а значит, излучения и поглощения наблюдаться не может. С этим мы столкнулись, когда определяли воздействие сил Кулона и Лоренца при орбитальном движении электрона вокруг протона [2, с. 10-37]. С аналогичной проблемой столкнулись и физики, когда посчитали что, так как магнитная сила всегда направлена перпендикулярно к скорости заряженной частицы, то она работы над частицей не совершает [25, с. 118]. Однако силового воздействия без энергетических затрат не существует, и эта проблема решается, если рассматривать движение частицы по каждой координате длины отдельно. При этом, в случае движения по окружности наблюдается излучение и поглощение для взаимосвязи через обмен с другими частицами. Иными словами, Шредингер, интуитивно, введя двойное дифференцирование по длине функции Ψ, тем самым осуществил переход к описанию движения через волновую функцию от противоположности с получением конечного результата, аналогичному для уравнения Гамильтона-Якоби. Однако, в уравнении (57), мы имеем дисбаланс в случае движения по окружности. Иными словами, есть формирование поглощения энергии под воздействием силы, но нет возможности изменить направление с потерей энергии через излучение в предыдущем направлении. Этот дисбаланс исключается для уравнения Гамильтона-Якоби за счёт наличия внешних сил. При этом мы имеем уравнение:

, (58)

Это уравнение в классике квантовой механики имеет решение в виде:

, (59)

Иными словами, добавление в аргумент функции значения U позволяет учитывать воздействие внешних сил на частицу. Понятно, что в замкнутой системе мироздания внешнее потенциальное поле U не может возникнуть чудом и оно формируется за счёт реакции на действие в виде движения частицы в нашей системе наблюдения.

Исходя из этого, теперь надо разобраться, что, собственно, даёт учёт взаимодействия корпускулярных и волновых свойств при законе сохранения количества за счёт перехода от возведения в квадрат первой производной функции от длины в уравнении Гамильтона-Якоби к двойному дифференцированию по длине этой же функции. Если волновая функция Ψ имеет вид (55), то мы имеем уравнение Гамильтона-Якоби (57). Однако, если исходить из (52), то здесь учитывается и изменение самого аргумента. То есть уравнение Шредингера может рассматривать процесс во взаимосвязи противоположностей, а не в варианте наличия одной противоположности по волновой функции Ψ с видом (55). При этом должно соблюдаться условие закона сохранения количества, так как объект не исчезает в результате движения.

В нашем случае, с учётом электромагнитных функций [1, с. 5-36], мы будем иметь вид без нормировочного коэффициента в виде величины постоянной Планка:

, (60)

В итоге получаем равенства:

, (61)

С учётом (60) и поскольку волновая функция Ψ в результате данного преобразования должна входить во все члены лишь множителем, мы можем её сократить. В итоге получаем:

, (62)

При учёте волновой функции Ψ вида (60) в одной системе наблюдения и волновой функции от аргумента в противоположной системе наблюдения, с учётом того, что дифференцирование соответствует условиям Дирака вида (56), мы имеем уравнение:

, (63)

Иными словами, мы показали переход от гармонического осциллятора (15) к верхнему уравнению в (16) на основе полного уравнения Гамильтона-Якоби с учётом внешних сил в виде потенциальной энергии, и с изменением аргумента S при функции Ψ. Это, с учётом (42) и (43) соответственно означает, что электрические и магнитные силы в одной системе наблюдения определяются движением по уравнению гармонического осциллятора в другой системе наблюдения. При этом наличие движущихся частиц есть в обеих глобальных противоположностях, и обмен между ними происходит через взаимное излучение с поглощением.

Собственно движение однозначно связано с наличием магнитной силы, которая в противоположности переходит в электрические силы на основании электромагнитного континуума. Поэтому, для рассмотрения образования собственного магнитного момента отдельной частицы необходимо рассмотреть её отдельное движение в противоположности по орбите. В этом случае мы должны представить суть наличия сторонних токов, которые формируют магнитное поле в нашей системе наблюдения, в системе наблюдения от времени, где они отображаются через движение реальных частиц.

Из классики электродинамики орбитальный магнитный момент вычисляется следующим образом [26, с. 159]. Пусть электрон движется со скоростью v по орбите r (рис. 1).

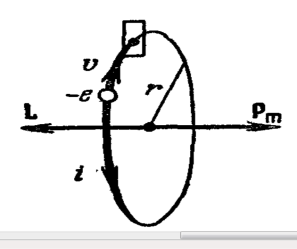
Рис. 1. Движение электрона по орбите

Через площадку, расположенную в любом месте на пути электрона, перемещается в единицу времени заряд еv_об, где е – заряд электрона, а v_об число оборотов в секунду. Следовательно, движущийся по орбите электрон образует круговой ток силы I=ev_об. Поскольку заряд электрона отрицателен, направление движения электрона и направление тока противоположны. Магнитный момент создаваемого электроном тока равен:

, (64)

Произведение даёт скорость движения электрона v, поэтому можно написать:

, (65)

Момент по (65) обусловлен движением электрона по орбите, вследствие чего называется орбитальным магнитным моментом электрона. Направление вектора р_m образует с направлением тока правовинтовую, а с направлением движения электрона левовинтовую систему. Движущийся по орбите электрон обладает моментом импульса:

, (66)

Вектор L – называют орбитальным механическим моментом электрона. Он образует с направлением движения электрона правовинтовую систему. Следовательно, направления векторов р_m и L противоположны. Отношение магнитного момента элементарной частицы к её механическому моменту принято называть магнитомеханическим (или гиромагнитным) отношением. Для электрона с учётом связи скорости света с массой электрона оно равно:

, (67)

Казалось бы, что ошибок нет, но вот тут надо заметить, что есть парадокс из-за наличия числового значения заряда , так как эта величина в формулу уравнения энергии Эйнштейна не входит. В теории Дирака [27, с. 349-350], которая следует из формулы энергии Эйнштейна, заряд элементарных частиц равен . Более того, мы имеем расхождение и с формулами Луи де Бройля, где энергия частицы, а значит и магнитного поля, зависит от импульса. При этом в формуле Луи де Бройля отсутствует количественное значение заряда . Кроме того, в [3, с. 5-44] мы показали, что начальная энергия волновых процессов, с наличием источника возбуждения, зависит от импульса, а не от количественного значения элементарного заряда. Это видно из формулы (37) с переходом к иной системе наблюдения через скорость света.

В этом случае мы имеем некую частицу с движением в противоположности с отражением всей кинетической энергии движения в окружающей среде распространения, через константы электрической и магнитной проницаемости. Отсюда формирование орбитального магнитного момента частицы не связано значением константы заряда , который связан с системой измерения для подгонки под результат. Следовательно, мы должны опираться на теорию Дирака при . В этом случае гиромагнитное соотношение имеет величину . Это означает, что никакой количественной разницы за счёт заряда элементарной частицы не может быть, так как иное бы означало расхождение в количественном плане при обмене между волновыми и корпускулярными свойствами. Значение гиромагнитного соотношения говорит о том, что орбитальное движение частицы не полностью определяет волновые свойства и соответственно общий магнитный момент. Как показывает практика помимо магнитного момента, формируемого за счёт орбитального движения, есть магнитный момент, связанный с вращением самой частицы (спин). Собственно, это следует и из уравнений гармонического осциллятора (15) и (49). При этом, так как принцип формирования связан в обоих случаях с корпускулярным вращением (иное противоречит корпускулярно-волновому дуализму), то для гиромагнитного соотношения для магнитного спина получаем . Однако если замкнутое движение, дающее магнитный момент при орбитальном движении связано с вращением электрона вокруг протона, то суть необходимости возникновения вращения самой частицы с точки зрения нашей системы наблюдения не имеет объяснения. Отсюда соответственно стоит вопрос о происхождении такого магнитного спина дополнительно к магнитному орбитальному моменту. При этом мы учитываем, что любой элементарный объект Мироздания должен отражаться как через пространственно-временное искривление (что связано с движением), так и через электромагнитные составляющие. В едином объекте одно не может существовать без другого в силу взаимосвязи через обмен с соблюдением закона сохранения количества. В противном случае объект без полного описания через пространственно-временное искривление и электромагнитные составляющие не соответствует замкнутой системе Мироздания. Данная проблема с собственным вращением частицы с образованием магнитного спина решается на основе нашей теории, где волновые электромагнитные свойства в одной противоположности формируют корпускулярные свойства в другой противоположности, и наоборот. Иными словами, созданные за счёт движения частиц в противоположной системе наблюдения, электромагнитные составляющие дают образование собственного вращения элементарной частицы в нашей системе наблюдения с формированием магнитного спина. По сути мы имеем аналогию с двойственностью образования пространственно-временного искривления по СТО и ОТО Эйнштейна, когда в одном случае по СТО пространственно-временное искривление формируется за счёт движения объекта в нашей системе наблюдения, а в другом случае по ОТО пространственно-временное искривление формируется за счёт движения в противоположности с наличием излучения электромагнитных составляющих. Если исходить из уравнения гармонического осциллятора (49), то магнитный спин определяется потенциальной энергией окружающей среды. Отсюда пространственно-временное искривление, связанное с этой потенциальной энергией, а это аналогично наличию электрических сил в противоположности, формирует вращение и магнитный спин частицы, что даёт необходимое излучение для обмена между противоположными зарядами, которые отображаются через объекты длины и времени. Таким образом, принцип образования магнитного орбитального момента и магнитного момента от спина, связан с взаимодействием противоположностей в виде кинетической и потенциальной энергии самой частицы. Соответственно, так как мы имеем связь противоположностей через скорость света, то пространственно-временное искривление за счёт потенциальной и кинетической энергии в каждой точке окружающей среды формируется на основе электрических и магнитных сторонних токов по (33) в виде:

, (68)

Иными словами, противодействие между противоположностями, представленными как орбитальный магнитный момент и магнитный спин выражается в соответствии с СТО и ОТО Эйнштейна в силу замкнутости Мироздания. И это также было замечено физиками в квантовой механике [7, с. 317-318] где магнитный спин в нерелятивистском случае вычислялся по формуле:

, (69)

Здесь ‒ масса электрона, ‒ двухрядная матрица Паули.

Двухрядная матрица Паули не влияет на количественное соотношение. Значение заряда по теории Дирака и нашей теории равно , соответственно . Далее учитываем, что и разница на величину связана с переходом от движения по длине окружности к величине радиуса частицы. Однако для размеров электрона не может быть величины меньше, чем постоянная Планка h, так как только по длине окружности выражаются изменения и обмен с излучением и поглощением, то есть электрон как реальный объект взаимодействия определяется излучением и поглощением именно по длине окружности. Собственно ‒ это тоже не наша выдумка и с учётом нашей теории следует из классической электродинамики [28, с. 276] в виде уравнения:

, (70)

Отсюда имеем:

, (71)

Отметим, что данное представление в (71) соответствует гипотезе Уленбека и Гаудсмита, по которой, собственный механический момент электрона равен [29, с. 272]. Разница в нормировке связана с выбором системы исчисления и наблюдения, и мы должны отметить, что ни одна реальная величина не может быть меньше постоянной Планка h. Иными словами, использование правил по нашей теории, при подстановке в выражения формул квантовой механики, привело к тому, что начальный магнитный спин стал интерпретироваться как механический собственный магнитный момент электрона, с величиной меньшей постоянной Планка , что также означает подгонку под результат в квантовой механике. Однако мы не должны выдумывать гипотезы, а должны опираться на реальные физические законы. В этом случае гиромагнитное отношение для любой вращающейся элементарной частицы с учётом нашей теории должно быть равно , что означает переход от механического момента к магнитному моменту. Собственно, иное исключает однозначную связь вращения с магнитными силами. Но, корпускулярные свойства в виде механического момента и электромагнитные волновые свойства ‒ это противоположности, связанные обратно-пропорциональной связью. Это означает, что при переходе от механических свойств к электромагнитным свойствам, так же как в (41) мы должны учесть связь противоположностей, образующих магнитные моменты через значение с², которое аналогично связи Е=m₀c². Отсюда с учётом нашей теории и поправок магнитный спин будет определяться начальным гиромагнитным соотношением:

, (72)

Далее физики отмечают, что при переходе к релятивистскому случаю необходимо вместо массы подставить её релятивистское значение . В результате имеем:

, (73)

Соответственно, чем больше скорость частицы, тем меньше магнитный спиновый момент, что наблюдается на практике. При этом, так как гиромагнитное отношение связано с массой, мы получаем зависимость этой величины с учётом СТО и ОТО Эйнштейна аналогично зависимости с точки зрения длины или времени. Мы видим, что отличие (73) от нижней формулы в (68) в плане числовых значений связано с коэффициентом ½. Это объясняется тем, что в электромагнитной волне рассматривается взаимодействие двух противоположных частиц, отражающих объекты длины и времени, а не одной частицы. Выше мы отмечали, что гиромагнитное соотношение для орбитального движения частицы с формированием магнитного момента также определяется соотношением . Но, в этом случае импульс частицы возрастает за счёт значения массы, а значит, растёт с ростом энергии и формируемый орбитальный магнитный момент. Иное исключало бы однозначную связь энергии и силы. С учётом релятивистского эффекта, так как стоит в знаменателе, мы будем иметь соотношение для магнитного орбитального момента:

, (74)

Понятно, что мы имеем соответствие с верхней формулой (68). Таким образом формирование общего магнитного момента определяется взаимодействием противоположностей в объекте от длины и времени в соответствии с СТО и ОТО Эйнштейна с соблюдением инвариантности магнитного поля от системы отсчёта. Так же понятно, что противодействие противоположностей выражается через обратно-пропорциональную связь относительно величины .

В результате для общего начального магнитного момента получим:

, (75)

Иными словами, магнитная составляющая отражает частицу в виде объекта длины в противоположности в состоянии покоя или объект времени, движущийся со скоростью света. При этом мы имеем однозначную связь движения и образуемого общего магнитного момента. Соответственно из-за связи противоположностей через скорость света и смене по этой причине электрических сил на магнитные силы, и наоборот, можно считать, что магнитный спин связан с наличием пространственно-временного искривления (по сути это аналог электрических сил), создаваемым в противоположности за счёт корпускулярного движения.

Как мы отмечали выше, движущийся в противоположной системе электрон отображается протоном в нашей системе наблюдения, и здесь влияние скорости движения в противоположности v_пр на собственный магнитный момент определяется через массу протона. Собственно, это также не наша выдумка и было отмечено физиками в [7, с. 317-318]. Отсюда в квантовой механике получено выражение:

, (76)

Здесь ‒ масса протона.

Надо отметить, что отношение массы протона к массе электрона в физике не имеет обоснования (из-за представления протона через кварки), но это отношение массы протона к массе электрона было получено в нашей теории. С учётом нашей теории масса протона вычисляется исходя из волнового сопротивления среды распространения с учётом максимума энергии излучения по формуле Планка с учётом коэффициента 4,965. Здесь мы учитываем, что в отличие от системы СИ у нас отношение , а не просто число . Это связано с тем, что в системе СИ или СГС не учитывается различие констант электрической и магнитной проницаемости на скорость света как противоположностей по аналогии с длиной и временем. Это означает парадокс, когда противоположности, отражённые через константы электрической и магнитной проницаемости, не имеют отличия, связанного со скоростью обмена (скорости света), то есть не соблюдается правило противоположностей с подчинением СТО и ОТО Эйнштейна, что исключает представление этих констант в виде противоположных объектов длины и времени. А это означает, что нет реального отображения констант в объектах Мироздания, и тогда для системы Мироздания они не существуют. В итоге получаем уравнение для отношения массы протона к массе электрона:

, (77)

Понятно, что некоторое небольшое отличие от практики (1836,1) в числовом значении есть, и оно связано с тем, что наши расчёты выполнены для более общего случая с делением только на протон и электрон. Кроме того, при динамике обмена обязательно должна быть энергия с соответствующей массой для излучения. Выше на основе уравнения (62) мы показали решения на основе отдельного представления орбитального и спинового магнитного момента как противоположностей от объектов длины и времени. При этом использовалась волновая функция вида . Далее учитываем интегральное значение выражения кинетической энергии движения частиц в противоположности, которые определяют в нашей системе наблюдения наличие протона. Отсюда аргумент волновой функции можно выразить через электрическую проницаемость . Здесь значение учитывает коэффициент 4,965 для условия стабильного состояния протона на пике излучения по формуле Планка [30, с. 30-31] при термодинамическом равновесии. Кроме того, мы учитываем связь импульса и энергии в аргументе волновой функции в виде Е=ср, аналогично такой же связи для длины и времени. В этом случае мы будем иметь волновую функцию для решения уравнения (62) в виде:

, (78)

Отсюда с учётом следует решение (62):

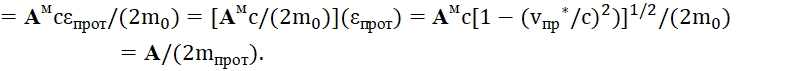, (79)

Иными словами, средняя интегральная кинетическая энергия от орбитального движения частицы в одной противоположности определяет магнитный спиновый момент частиц в другой противоположности при замкнутой системе от длины и времени. При этом необходимо учесть, что магнитные и электрические силы через силу Лоренца и Кулона в противоположностях при связи через скорость света меняются местами в соответствии с электромагнитным континуумом [4, с. 273]. В этом случае мы имеем общее магнитное поле, определяемое как орбитальным, так и спиновым движением, так как и в том и другом случае пространственно-временное искривление формируется за счёт движения, но в противоположностях. Отсюда, отдельная частица представляется через взаимодействие составляющих её противоположностей, и при этом в этом случае с учётом последней формулы в (14) мы должны иметь общую функцию в виде:

, (80)

Не надо думать, что такое представление наша выдумка. Данный вид уже следовал из применения в электродинамике комплексных значений электрической и магнитной проницаемости. Кроме того, чтобы оправдать связь массы покоя с частотой, Луи де Бройль постулировал существование волнового поля:

, (81)

Не зная, что собой физически представляет это волновое поле, физики стали интерпретировать его как функцию, которая характеризует вероятность. Но мы отметим, что при эксперименте Дэвиссона и Джермера [10, с. 63] с однозначно получаемой формулой, случайностей нет. И это как раз исключает связь функции Луи де Бройля со случайными процессами, По сути Луи де Бройль утвердил представление объектов мироздания в одной противоположности в виде волновых процессов, а в другой противоположности в виде корпускул с массой покоя. Отсюда следует, что способ отражения корпускулярно-волновых свойств, исходя из функции Луи де Бройля (81), с соответствующим представлением значения Ψ₀ по геометрии Минковского через экспоненциальную функцию с учётом нижней формулы (14), может быть представлен в виде:

, (82)

При таком представлении объект имеет корпускулярно-волновое отображение в обеих противоположностях и за счёт мнимой единицы происходит смена корпускулярного представления на волновое представление, и наоборот. То есть, если в аргументе функции (78) значения по энергии и импульсу при времени и длине выражены в единой системе наблюдения, то в формуле (80), они отображены как противоположности. Соответственно, противоположности в одной системе наблюдения и компенсацией друг друга, представляют собой единое целое в другой противоположной системе наблюдения (иначе отличий нет). В этом случае уравнение вида (62) должно давать разные результаты в зависимости от системы наблюдения, что также не наша выдумка и было использовано при калибровке Лоренца (это было показано в (25)). Далее из (79) мы учитываем, что С учётом правила дифференцирования по Дираку (56), а также из условия, что разность в противоположности меняется на сумму, подстановка в (62) даст решение аналогичное по виду нижнему уравнению (68) . С учётом имеем:

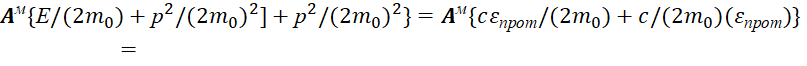
, (83)

Иными словами, мы имеем симметричный закон отображения составляющих, но с точки зрения системы наблюдения от векторного потенциала А. При этом соблюдается закон сохранения количества между корпускулярными и волновыми свойствами.

Таким образом, мы обосновали наличие значений магнитных моментов  (волновые функции) на основе вращательных движений с учётом соответствия гиромагнитному отношению. Однако помимо магнитных моментов связанных с орбитальным и спиновым значением в нашей системе наблюдения на практике обнаружили и так называемые аномальные магнитные моменты (например, для протона и нейтрона), которые физики попытались объяснить на основе виртуальных частиц, таких как кварки и глюоны [31, с. 297]. В соответствии с этой гипотезой, за которую Гелл-Манну дали Нобелевскую премию по физике, все элементарные частицы построены из трёх частиц, названных кваркам. Этим частицам приписываются дробные квантовые числа, в частности электрический заряд, равный +2/3, -1/3, -1/3 соответственно для каждого из трёх кварков. Соответственно для всех кварков при этом спин равен ½. Каждому кварку приписывается одинаковый магнитный момент , величина которого из теории не определяется. Понятно, что разница в значении электрического заряда для кварков с наличием одного и того же магнитного момента означает уже то, что физики отделили электрические силы от магнитных сил, то есть придумали неоднозначные законы связи электрических и магнитных сил. Далее, так как значение магнитного момента кварка невозможно никак вычислить, то делается очередная подгонка под результат при которой значение магнитного момента кварка выбирается равной общему значению магнитного момента протона, с учётом, как аномального магнитного момента, так и обычного магнитного момента , то есть . Для нейтрона .

Соответственно мы сразу видим парадокс в вычислении аномального магнитного момента для нейтрона с помощью магнитного момента для кварка, который имеет зависимость отдельную зависимость от магнитного момента Дирака, который зависит от скорости движения. При этом из экспериментальных данных опытов Блоха-Альвареца [32, с. 319], нейтрон обладает аномальным магнитным моментом, равным . Понятно, что мы, в отличие от физиков, не должны придумывать частицы и явления, которые не опираются на известные практические физические законы. В частности, мы должны учитывать однозначную связь корпускулярных и волновых свойств, где движение однозначно связано с наличием магнитных моментов. Доказательство связи с учётом получения гиромагнитного соотношения для орбитального движения и спина, было показано выше и не является нашей выдумкой. Понятно, что и аномальный магнитный момент не может формироваться чудодейственным способом, и он тоже должен быть связан с движением. Однако отсутствие понимания наличия противоположностей с наличием собственных систем наблюдения помешало физикам понять истинную причину появления аномальных магнитных моментов. Поэтому, они вышли из тупика за счёт виртуальных мезонов () [33, с. 240]. Здесь мы имеем обмен, в соответствии с виртуальным процессом:

, (84)

Нейтрон (n) часть времени проводит в виртуальном состоянии в виде протона (р) и отрицательного мезона (). Орбитальное движение отрицательного мезона () приводит к возникновению наблюдаемого у нейтрона отрицательного магнитного момента. Аномальный магнитный момент протона (), вместо одного ядерного магнетона () физики также объясняют орбитальным движением положительного мезона () в течение того промежутка времени, когда протон находится в виртуальном состоянии (). Иными словами, физики, при использовании виртуальных частиц, не ушли от самого принципа образования существования магнитного момента за счёт движения. Они при отсутствии понимания логики необходимости существования разных систем наблюдения от противоположностей придумали орбитальное движение виртуальных частиц, и тем самым пришли к чудесам. Мы же изначально исходим из зависимости представления объектов с учётом разных систем наблюдения из противоположностей, так как иное противоречит необходимости симметрии между противоположностями с соблюдением условия сохранения количества.

Понятно, что противоположности воздействуют друг на друга с поддержанием термодинамического равновесия. В этом случае противоположности связаны между собой как аргумент функции и сама функция. Это связано с тем, что одна противоположность выступает как воздействующая величина, а другая является объектом воздействия. Соответственно законы формирования корпускулярных и волновых свойств в противоположностях совпадают. При этом аргумент функции, который характеризует некий объект Мироздания, например, вида (78) с функцией должен иметь реальное воплощение с отражением через корпускулярные и волновые свойства, так как иначе воздействия (от нереального не отражённого в корпускулярно-волновом виде), как такового не получить. Исходя из нашей теории, протон в противоположности представляет собой движущийся электрон, и отсюда мы получили его собственный ядерный магнитный момент с учётом орбитального движения в противоположности. Однако помимо орбитального движения элементарной частицы в противоположности, существует и спиновое вращение, которое определяется от кинетической энергии движения с учётом при этом излучения всех частиц уже в нашей системе наблюдения. Соответственно связь магнитного момента со спиновым вращением отражается через значение гиромагнитного соотношения, где учитывается, что кинетическая энергия, взаимодействующая с элементарной частицей, также в соответствующей системе наблюдения выражается через электрон и протон с разницей масс, иначе при представлении через электрон и позитрон будет неустойчивое состояние с аннигиляцией. При этом эта кинетическая энергия в аргументе волновой функции для спина частицы, которая представляется движущимся электроном (в нашей системе наблюдения это протон), отражается на основе суммы от воздействия этих противоположных частиц, характеризующих кинетическую энергию (фотон) электрона. Поэтому мы должны аргумент функции (78), представить с учётом смены вычитания на сложение. Отсюда формирование аномального магнитного момента через движение, связанное со спином, в противоположной системе наблюдения, отражается через гиромагнитное соотношение с учётом изменения по СТО и ОТО Эйнштейна в виде:

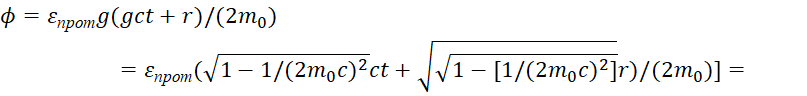
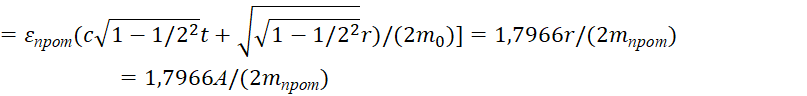, (85)

Здесь, ‒ аргумент волновой функции Луи де Бройля по (82), , r=сt=A. Таким образом, аргумент имеет выражение (что связано с движением в соответствующей системе наблюдения) по закону (85), что определяет и наличие соответствующего магнитного момента. Как будет показано ниже закон в виде это тоже не наша выдумка, и он также следует из уравнения гармонического осциллятора. Отсюда при сложении с ядерным магнитным моментом протона (79) мы получим полный магнитный момент протона с учётом аномального магнитного момента в виде:

, (86)

Необходимо иметь в виду, что в данном случае система наблюдения связанна с отображением взаимодействия через магнитные составляющие. Так как магнитный спин электрона (в нашей системе наблюдения это протон), формируемый в противоположности зависит от кинетической энергии всех частиц в нашей системе наблюдения по условию термодинамического равновесия, то у него нет зависимости от скорости движения самого протона в нашей системе наблюдения. Отличие аномального магнитного момента от нейтрона заключается в том, что он формируется за счёт спинов от двух частиц, протона, и электрона. При этом, так как электрон и протон являются противоположностями, то их движения с точки зрения обычных магнитных моментов Дирака имеют противоположные знаки и компенсируют друг друга. То есть орбитальное движение электрона в соответствующей системе наблюдения, дающее магнитный орбитальный момент, компенсируется за счёт орбитального движения позитрона (в системе наблюдения электрона ‒ это протон) тоже в соответствующей системе наблюдения. Аномальные магнитные моменты, от спинов электрона и позитрона (с учётом рассмотрения их в своих системах наблюдения), которые наблюдаются в противоположности и дают в нашей системе наблюдения нейтрон, наоборот, складываются. Причём составляющие в аргументе функции для протона складываются, а для электрона (в противоположности) сумма составляющих в аргументе функции сменяется на разность. В противном случае нет основного отличия для противоположностей, когда сумма в одной противоположности означает разность в другой противоположности. В итоге общую сумму от двух противоположных частиц для общего аномального магнитного момента нейтрона, выраженного через аргумент функции можно представить в виде в виде:

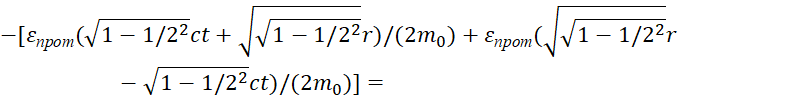
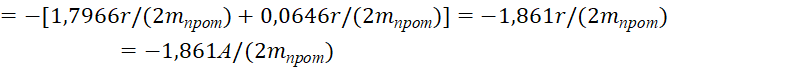, (87)

Отрицательный знак аномального магнитного момента означает, что системы наблюдения нейтрона и того же протона являются противоположными. Действительно, нейтрон в нашей системе наблюдения распадается на электрон, протон и антинейтрино, что интерпретируется в противоположной системе наблюдения как движущейся электрон (в нашей системе наблюдения ‒ это антинейтрино) с кинетической энергией (в нашей системе наблюдения ‒ это электрон и протон). Протон тоже интерпретируется в противоположности как движущаяся частица, но здесь эта частица отражается, например, как электрон, а кинетическая энергия от противоположности представляется дополнительной массой в нашей системе наблюдения. Полученный нами результат для аномальных магнитных моментов совпадает с вариантами подгонки под результат на основе гипотезы Гелл-Манна. Однако как было сказано выше, из экспериментальных данных опытов Блоха-Альвареца, нейтрон обладает аномальным магнитным моментом, равным . Понятно, что различие на 0,049 может быть связано с условиями проведения эксперимента, но мы склонны считать, что это связано с тем, что нейтрон не является устойчивым и подвержен распаду. Распад по нашей теории связан с тем, что в противоположной системе наблюдения не соблюдается условие термодинамического равновесия, и в этом случае электрон находится на орбите выше, чем это нужно для соблюдения термодинамического равновесия, что даёт излучение в противоположности и распад нейтрона на антинейтрино, протон и электрон в нашей системе наблюдения. В этом случае можно считать, что, так как магнитный момент определяется более высокой скоростью движения , то увеличение аномального магнитного момента нейтрона происходит за счёт добавочной скорости движения, что может быть учтено поправкой в виде:

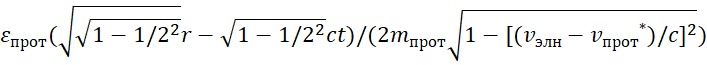, (88)

Отметим, что для любой частицы мы исходим из её соответствия корпускулярно-волновому дуализму в соответствии с функцией Луи де Бройля по (82). Именно в этом случае аргументы функции и выступают как воздействующие величины с наличием действия и противодействия (электрические и магнитные силы). Следует отметить, что вычисление магнитного момента с соответствующей энергией по формуле (85) – это не наша выдумка. Нечто подобное было применено при нахождении энергии ротатора в квантовой механике [34, с. 195] в виде:

, (89)

При имеем вид:

, (90)

Понятно, что член , также в квантовой механике связали с аналогом классической функции Гамильтона при классическом вращении в виде [35, с. 190]:

, (91)

Здесь: , а . Здесь вращение связано с центробежной силой и чем больше радиус r, тем выше центробежная энергия и сила. Однако в теории водородоподобного атома в квантовой механике [36, с. 208] уравнение Шредингера представили в виде:

, (92)

При этом классический аналог представляется в виде:

, (93)

Для квантового случая ввели эффективную потенциальную энергию электрона в виде:

, (94)

При этом физики предположили, что второй член в (94) связан с центробежными силами, то есть . Сравнивая с формулой (85), мы видим, что различие со значением g(g+1) связано с тем, что в волновой функции есть член . В нашем варианте в (60) у нас такой нормировки нет, в силу того, что аргумент также представляет собой функцию. Кроме того, мы рассматриваем круговое движение при вращении (спин), дающее пространственно-временное искривление, а не наличие неких центробежных сил. Подчеркнём, что понятие центробежных сил, а также сил гравитации, по нашей теории должно иметь представление через силу Кулона и силу Лоренца как единственных сил, отражающих взаимодействие противоположностей. Соответственно здесь r отражает радиус, связанный с частотой вращения, а – длину окружности пути прохождения при вращении. Собственно такой подход отражения замкнутого движения (другой вариант исключён в силу того, что не будет взаимодействия через излучение и поглощение) основан на получении магнитных свойств с наличием гиромагнитного соотношения. В этом случае при связи частоты и скорости по (21) в соответствии с формулой Луи де Бройля и с учётом нашей теории, мы получаем:

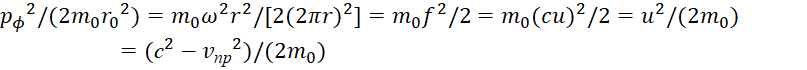, (95)

Соответственно для движущейся частицы с наличием спина мы получаем уравнение гармонического осциллятора в виде:

, (96)

Здесь мы учитываем, что в реальности не существует одномерной модели гармонического осциллятора, и движение происходит по кругу. В этом случае прямолинейное движение определяется кинетической энергией тангенциальной составляющей , которая связана с изменением направления, что не может происходить без излучения.

Понятно, что при нормировке на Е=hf в (96) мы имеем связь противоположностей по уравнению окружности вида:

, (97)

Соответственно мы видим, что добавление ещё одного члена в (92) и (93) в виде , не вписывается в замкнутую систему взаимодействия двух противоположностей. Собственно этого члена нет и в уравнении гармонического осциллятора на основе уравнения Шредингера, которое имеет вид [37, с. 90]:

, (98)

Более того, член выступает как потенциальная энергия сдерживающих сил для движения частицы, что, собственно, замещает член . Отсюда в (92) аналог члена рассматривается как центробежная сила, противодействующая энергии , а в (97) этот член выступает как энергия сдерживающих сил. Такой двузначный подход стал необходим физикам, что благодаря эффективной потенциальной энергии электрона (94) они оправдали подгонку под результат с потенциальной ямой для волновой функции частицы, характеризующей вероятность нахождения в потенциальной яме по рисунку 2.

Рис. 2. График зависимости эффективной потенциальной энергии (сплошная кривая) от расстояния по формуле (93). Штрихпунктирной кривой показан ход волновой функции, которая характеризует вероятность нахождения частицы

Иными словами, учёные тем самым утвердили в физике чудеса телепортации с прохождением через потенциальный барьер. В этом случае законы физики теряют смысл, так как там, где чудеса законы физики не нужны.

Отметим, что закон g²+g, который интуитивно использовали физики, а также закон g²‒g, следуют из равенства от гармонического осциллятора вида . Здесь можно записать:

, (99)

Значения скоростей v_пр и v и импульсов относятся к противоположностям с учётом обратно-пропорциональной связи между противоположностями. При условии инвариантности, а также, исходя из закона сохранения количества, имеем равенство m₀v_пр=m₀v. Отсюда при представлении значения m₀v_пр через значение m₀v мы осуществляем переход от системы наблюдения от всего Мироздания к системе наблюдения в одной противоположности. Собственно такой переход осуществил и Бор сделав замену при определении первой боровской орбиты. В этой общей системе наблюдения от одной противоположности имеем:

, (100)

Иными словами, законы g²+g и g²‒g ‒ это результат отображения закона замкнутого взаимодействия противоположностей при наблюдении процессов из одной общей системы на основе выполнения уравнения гармонического осциллятора. Чтобы перейти к виду для отображения аномального магнитного момента нейтрона (87) мы должны изменить нормировку, так как рассматривается в движении конкретный объект Мироздания, а не всё Мироздание в динамике взаимодействия противоположностей. Отсюда имеем представление аномального магнитного момента нейтрона в виде:

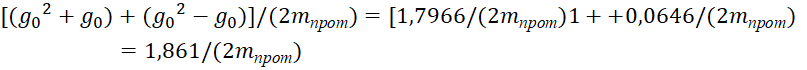, (101)

Соответственно , это конкретное число, связанное с гиромагнитным соотношением 1/(2m₀) на основе движения частицы и пересчётом механического момента в магнитный момент. Только в этом случае соблюдается условие зависимости магнитного спина в противоположности от общего значения кинетической энергии в нашей системе наблюдения. В противном случае мы бы не имели связи каждого объекта мироздания с другими объектами.

В результате следуют следующие выводы:

1. Учёные принципиально не могли решить задачу возникновения аномальных магнитных моментов, так как опирались на существование одной единственной системы наблюдения, пренебрегая тем самым наличием противоположностей и корпускулярно-волновым дуализмом.
2. Само наличие магнитного спина физики также не могли объяснить, то есть никакой классической теории спина по их представлению не существует [29, с. 272]. В нашей теории магнитный спин связан с отображением кинетической энергии излучения частиц в противоположности, что выражается через вращение в нашей системе наблюдения с соответствующим пространственно-временным искривлением. Иными словами, у нас магнитный спин это не некое квантовое число как в квантовой механике, а реальный физический процесс формирования магнитного поля за счёт движения.
3. Попытка объяснения физиками аномальных магнитных моментов на основе виртуальных мезонов и кварков связана с чудесами соотношения неопределённостей Гейзенберга, телепортацией и деления протона и нейтрона, а также и других известных частиц на виртуальные и более мелкие. Это противоречит идее Ломоносова, по которой, объект состоит из того, на что он распадается. В нашей теории мы опираемся на идею рассмотрения процессов взаимодействия в зависимости от системы наблюдения. Это позволяет понять переход от простых объектов Мироздания (электронные и мюонные нейтрино и антинейтрино) к более сложным объектам, таких как фотон, электрон, позитрон, протон и нейтрон с учётом преобразования волновых свойств в корпускулярные, и наоборот, в зависимости от системы наблюдения.
4. Отсутствие понимания логики взаимодействия, на основе противоположностей, привело к тому, что учёные стали рассматривать движение электрона в атоме водорода в виде волновой функции, характеризующей вероятность нахождения электрона в виде орбиталей, с наличием потенциальной ямы. Это не соответствует классике орбитального движения уже потому, что при одной и той же энергии возможно наличие разных орбит, что видно из рисунка 2.
5. В этой статье мы показали, как на основе классической теории решается задача наличия магнитного спина и аномальных магнитных моментов с совпадением теоретических расчётов и экспериментальных данных при использовании уже известных формул на основе логики теории Мироздания.