Корни квадратного трехчлена

Уравнение вида:

pх²+qх+r= 0, (1)

Где p, q, r – некоторые числа и p ≠ 0, x – неизвестное, называется квадратным уравнением.

Многочлен:

pх²+qх+r, (2)

Где а≠ 0, называют квадратным трехчленом; p – старший коэффициент, q – средний коэффициентом и r – свободный член квадратного трехчлена.

Значения аргумента х, при которых квадратный трехчлен pх²+qх+r равен нулю, называют корнями квадратного трехчлена. Иначе говоря, корнями трехчлена pх²+qх+r называют решения квадратного уравнения pх²+qх+r= 0.

Следовательно, задача решения квадратного уравнения (1) равносильна задаче нахождения корней квадратного трехчлена (2).

Корни квадратного трехчлена с комплексными коэффициентами в поле комплектных чисел. Рассмотрим квадратный трехчлен pх²+qх+r с произвольными комплексными коэффициентами, считая, что множество допустимых значений аргумента х – это поле комплексных чисел.

Сначала найдем корни квадратного трехчлена. Для этого, учитывая, что а ≠ 0, выполним тождественное преобразование:

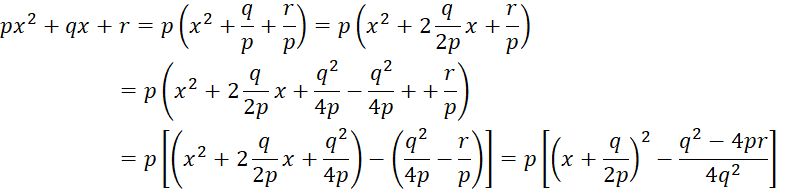
Следовательно,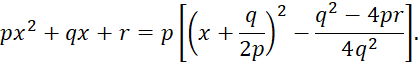

Такое преобразование квадратного трехчлена называют выделением полного квадрата.

Поскольку q≠0, то трехчлен тогда и только тогда будет равен нулю, когда:

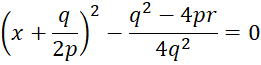, (3)

И, таким образом, корнями трехчлена будут такие значения x, при которых имеет место равенство:

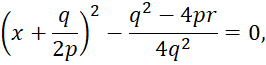
А значит, и равенство:

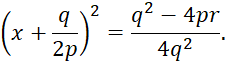
Из этого равенства получаем:

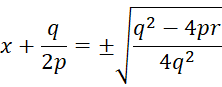
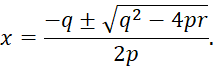
Таким образом, корнями квадратного трехчлена а значит и квадратного уравнения будут значения x, которые определяются следующей формулой:

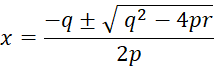, (4)

Пусть x₁ и x₂ – корни квадратного уравнения, то исходя из формулы (4):

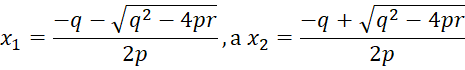, (5)

Пример. Найти корни квадратного трехчлена . По формулам (4) и (5) имеем:

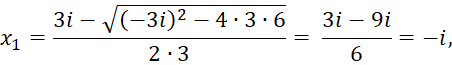
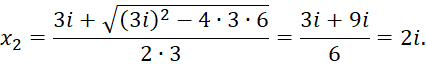
Выражение называют дискриминантом квадратного трехчлена (уравнения).

Поскольку коэффициенты p, q, r – числа комплексные, то и дискриминант d квадратного трехчлена будет числом комплексным (в некоторых случаях он может быть числом действительным).

Возможны случаи: d=0 и d≠0.

Трехчлен имеет два равных корня: x₁=x₂=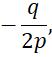 если дискриминант d=0 (4).

Если же дискриминант d≠0, то квадратный трёхчлен имеет два различных корня:

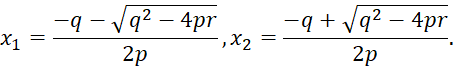
Наоборот, если квадратный трехчлен имеет два равных корня, то его дискриминант равен нулю, а если трехчлен имеет два различных корня, то его дискриминант отличен от нуля, так как. Если бы d=0, то в силу доказанного выше трехчлен имел бы двукратный корень.

Следовательно, теорема доказана.

Квадратный трехчлен с любыми комплексными коэффициентами имеет в поле комплексных чисел или двукратный корень, или два различных корня. Для того чтобы трехчлен имел двукратный корень, необходимо и достаточно, чтобы его дискриминант d был равен нулю; для того, чтобы он имел два различных корня, необходимо и достаточно, чтобы его дискриминант d был отличным от нуля.

Примеры:

1. Трехчлен 4ix²+8x–4i имеет двукратный корень: x₁=x₂=i; дискриминант этого трехчлена равен 0.
2. Трехчлен 4x²–10ix–4 имеет два неравных корня 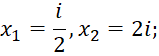дискриминант этого трехчлена равен

Корни квадратного трехчлена с действительными коэффициентами в поле комплектных чисел.

В том случае, когда коэффициенты p, q, r квадратного трехчлена действительные числа, его дискриминант тоже будет действительным числом, при этом он может быть равным нулю, большим нуля или меньшим нуля.

1. Рассмотрим случай, когда дискриминант . Пусть , где , тогда:

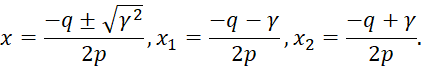
В этом случае трехчлен имеет два различных корня:

.

.

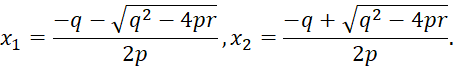
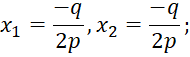В этом случае мы получили два равных между собой корня. Т. е. трехчлен имеет двукратный действительный корень.

2. Тогда где , значит Корнями квадратного трехчлена будут:

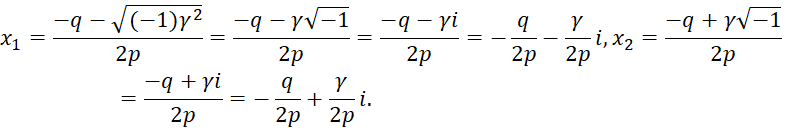
Получается, что корни трехчлена в этом случае комплексные сопряженные.

Наоборот, если корни квадратного трехчлена с действительными коэффициентами p, q, r действительные различные, то его дискриминант больше нуля.

Если трехчлен имеет двукратный корень, то его дискриминант равен 0, так как, в соответствие с выше доказанным, в противном случае трехчлен имел бы различные корни.

Если квадратный трехчлен с действительными коэффициентами имеет комплексные сопряженные корни, то его дискриминант меньшее нуля число, в противном случае он бы имел действительные корни.

Следовательно, мы доказали теорему.

Примеры:

1. Трехчлен x²–5x+6=0 имеет два действительных корня: x₁=3, x₂=2, так как дискриминант .
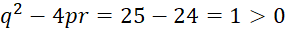2. Трехчлен 7x²-14x+7=0 имеет два равных между собой корня: x₂–x₂=1, т. к. его дискриминант q²-4pr=196-196=0.
3. Трехчлен 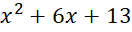имеет два комплексно сопряженных корня:

, так как его дискриминант .

Учитывая, что коэффициенты, корни, дискриминант квадратного трехчлена pх²+qх+r – это коэффициенты, корни и дискриминант квадратного уравнения pх²+qх+r=0, все доказанные нами утверждения, касающиеся квадратного трехчлена, будут справедливы и для квадратного уравнения.