Основные свойства неравенств

Неравенства, как и уравнения играют существенную роль во всех разделах современной математики.

Неравенство – это соотношение между двумя числами, которое указывает, какое из них больше и какое меньше. Для обозначения неравенства употребляют знак > или <, который направлен острием к меньшему числу. Например, если число (величина) p больше, чем число (величина) q то это записывается так: p > q или q < p. Другими словами, неравенства – это соотношения вида:

p > q, p < q

Если число m не меньше, чем число n, то записывается это так: или

Нестрогими неравенствами называются соотношения вида

Если неизвестно, какое из чисел p и q больше, а какое меньше, но известно, что они не равны, то это можно записать так: Соотношение такого вида тоже называют неравенством. Для обозначения неравенств часто употребляются знаки ∨ и ˅. Знак ˅ может заменить любой из символов тогда знаком ˄ обозначают символ противоположного смысла, т. е. соответственно

Неравенствами одинакового смысла называют неравенства, в которых левые части больше, чем их правые части, или левые части меньше, чем правые части. Неравенствами различного или противоположного смысла называют неравенства, если в одном из них левая часть больше правой части, а в другом левая часть меньше правой части. Например, неравенства 6 > 3 и 9 > 7 называют неравенствами одинакового смысла, а неравенства 3 > 1 и –1 < 9 называются неравенствами противоположного смысла.

Теорию неравенств можно построить только в упорядоченном поле. Такими являются среди числовых поля рациональных и действительных чисел. Мы будем рассматривать неравенства в этих полях.

Числа, которые больше нуля, называют положительными, а числа, которые меньше нуля – отрицательными. Число больше, чем число q, тогда и только тогда, когда разность p – q есть положительное число.

Основные свойства неравенств:

1. Если p > q и q > r, то p > r.

Это свойство транзитивности неравенств, непосредственно вытекающее из второго определения упорядоченного поля.

2. Если p > q, то p + r > q + r для любого числа r, т. е. если обе части неравенства сложить с одним и тем же числом, то это неравенство не изменится.

Следствие. Если всякое слагаемое из одной части верного неравенства перенести в другую, изменив при этом его знак на противоположный, то получится верное неравенство.

Если p + q > r, то, если прибавить к обеим частям неравенства –q, получим p > r –q, т. е., слагаемое перенесено из левой части в правую, поменяв знак на противоположный.

3. Если p > q, r > s, то p + r > q + s, т.е. если почленно сложить два неравенства одинакового смысла, то получится неравенство того же смысла.

Доказательство. Если p > q, то p + r > q + r, и если, r > s, то q + r > q + s.

Следовательно, по свойству транзитивности получаем, что p + r > q + s, что и требовалось доказать.

4. Если p > q, то pr > qr при r > 0 и pr < qr, при r < 0, а именно, знак неравенства не изменится, если обе части верного неравенства умножить на одно и то же положительное число, а если обе части верного неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.

Доказательство. Если p > q, то p – q > 0. Отсюда, разность pr – qr = r (p – q) имеет тот же знак, что и число r, если r – число положительное, то и разность pr – qr положительна, а значит pr > qr, а если число r отрицательное, то разность pr – qr меньше нуля, значит pr < qr.

5. Если p > q и r < s, то p – r < q – s, иначе говоря, если из данного верного неравенства почленно вычесть неравенство противоположного смысла, то получится неравенство одинакового смысла с данным.

Доказательство. Так как r < s, то – r > – s, значит, по выше доказанному свойству, p + (–r) < q + (–s), т. е. p – r < q – s.

6. Почленное умножение обеих частей верных неравенств дает положительное число, т. е. при p < q и r < s, где p, q, r, s – положительные числа, справедливо неравенство pr < qs.

Доказательство. Так как r и s – положительные числа, то из неравенства p < q получаем, что pr < qr, а из неравенства r > s получаем неравенство qr < qs, следовательно, pr < qs.

7. Если p > q > 0, то при любом натуральном , будем иметь т. е. неравенство, содержащее положительные члены не изменится, если обе части его возвести в степень с одним и тем же натуральным показателем.

Доказательство. При неравенство справедливо по условию. Предположим, что оно верно при где произвольно выбранное число из множества натуральных чисел, т. е. что Умножим неравенство почленно на неравенство p > q, имеем:

Иначе говоря, утверждение справедливо и при . Отсюда, в силу принципа математической индукции оно справедливо для любого натурального

Рассмотрим тождественное неравенство, которое применяется при решении многих задач.

Неравенство Коши. При любых действительных значениях выполняется неравенство:

Или, кратко:

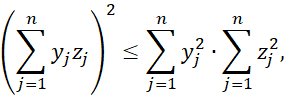
Притом, равенство имеет место тогда и только тогда, когда значения пропорциональны, т. е. когда

Доказательство. Приняв в тождестве Лагранжа:

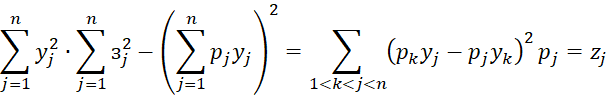
Будем иметь:

Так как при любых действительных значениях правая часть данного тождества, которая является суммой квадратов действительных чисел, является неотрицательной, то:

И, отсюда:

Равенство будет верным тогда и только тогда, когда все слагаемые правой части тождества равно нулю, т. е. когда:

Но если эти равенства выполняются, то и, следовательно,

Для любых положительных чисел выполняется неравенство причем равенство имеет место тогда и только тогда, когда:

.

Доказательство. Для любых действительных чисел выполняется неравенство а следовательно, и неравенство причем равенство имеет место тогда и только тогда, когда .

Если числа положительные, то, разделив обе части этого неравенства на получим:

Этим справедливость неравенства доказана.