Числовые функции и их роль в изучении арифметических свойств натуральных чисел

1. Число и сумма натуральных чисел. Мультипликационные числовые функции

1.1. Число и сумма натуральных делителей

Функции, заданные на множестве натуральных чисел и связанные с арифметической природой этих чисел, называют числовыми функциями. Примерами таких функций могут служить:

1. Число 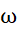(n) всех натуральных делителей n;
2. Сумма 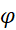(n) всех натуральных делителей числа n;
3. Число (n) натуральных чисел, меньших n и взаимно про­стых с n (функция Эйлера).

Выведем формулу, с помощью которой вычисляют (n), зная каноническое разложение n: . Нам уже известно, что любой делитель числа n имеет вид:

Где для любого j, , выполняются неравенства .

И потому показатель может принимать различных значений: 0, 1, ..., , показатель принимает различное значение, ..., показатель принимает различных значений. Другими словами, в кортеже () первая координата может принимать () значений, вторая – () значений, ..., т-я – () значений. Но число таких кортежей равно .

Таким образом, мы доказали следующую теорему:

Теорема 1. Если каноническая запись числа n такая, что:

, (1)

То число натуральных делителей n равно:

, (2)

Пример. Так как 80 = 2⁴ 5, то:

(80) = (4+1) (1 + 1) = 5  2 = 10.

Делителями числа 80 являются 1,2, 4, 5, 8, 10, 16, 20, 40, 80. Их число действительно равно 10.

А теперь формула для (n) – суммы всех натуральных делителей.

Пусть Рассмотрим произведение:

, (2')

Раскрыв скобки, получим сумму членов вида где при любом j, , выполняется неравенство .

A такие члены являются делителями n, и притом каждый делитель входит в сумму только один раз. Поэтому произведение (2') равно сумме всех делителей n, т. е. (n). Итак:

Но каждая сумма является суммой геометрической прогрессии со знаменателем . Применив формулу суммы членов геометрической прогрессии, получим:

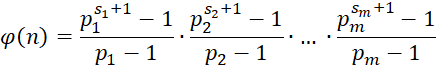, (3)

Таким образом, мы доказали следующую теорему.

Теорема 2. Если каноническая запись числа n имеет вид:

то (п) выражается формулой (3).

Пример. Найдем сумму натуральных делителей числа 180. Так как 180 = 2² З² 5, то:

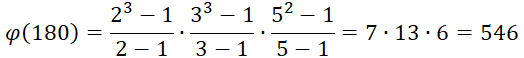
1.2. Мультипликативные числовые функции

Формулы для и являются частными случаями более общей формулы, связанной с мультипликативными числовыми функциями.

Определение 1. Числовая функция называется мультипликативной, если:

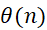1. определена для всех натуральных n, причем ;
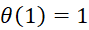2. для любых взаимно простых натуральных чисел n и k выполняется равенство:

, (1)

Примером мультипликативной функции может служить функция:

где – любое число, а . Действительно, и для любых натуральных п и k (даже не взаимно простых) выполняется равенство:

Докажем следующие свойства мультипликативных функций:

Теорема 3. Если числа попарно взаимно просты, а – мультипликативная функция, то:

, (2)

Доказательство будет проводить с помощью математической индукции. При равенство (2) верно по определению мультипликативности. Пусть уже доказано, что оно верно при m = i, и пусть – любые попарно взаимно простые числа. Тогда числа взаимно просты, и потому:

Но, так как равенство (2) верно при , то  и потому:

Итак, равенство (2) верно при m = 2 и из его справедливости при m = i следует справедливость и при . Значит, равенство (2), верно, для любого числа попарно взаимно простых сомножителей.

Следствие. Если каноническая запись числа n имеет вид:

, – мультипликативная функция, то:

Утверждение вытекает непосредственно из того, что числа попарно взаимно просты, и из теоремы 3.

Теорема 4. Если каноническая запись числа n имеет вид:

, – мультипликативная функция, то:

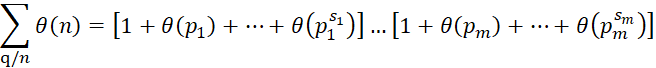, (3)

Где слева сумма распространена на все делители числа q.

Доказательство. Чтобы доказать формулу (3) достаточно раскрыть скобки в правой части и принять во внимание, что по теореме 4:

Причем – делитель числа .

Формулы для и выведенные выше, являются частны­ми случаями общей формулы (3). Чтобы вывести формулу для надо положить . Тогда слева получится сумма единиц, причем число слагаемых равно числу делителей n, т. е. , а справа – произведение чисел

. А формула для  получается, если положить (эта функция мультипликативна). Тогда слева получится сумма всех делителей n, т. е. а справа – произведение:

С помощью формулы (3) можно вывести новые формулы. Например, полагая выводим, что при

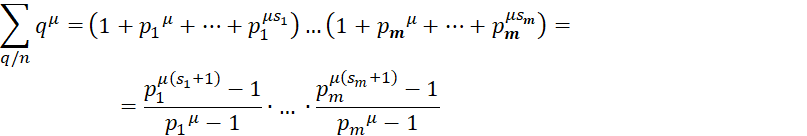, (4)

Теорема 5. Если и – мультипликативные функции, то их произведение тоже является мультипликативной функцией.

Доказательство. Мы имеем:

и если , то:

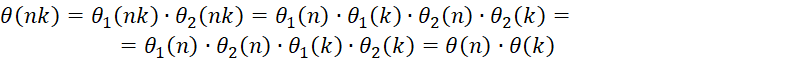
2. Распределение простых чисел. Асимптотический закон распределения

2.1. Доказательство бесконечности множества простых чисел (доказательство Эйлера)

Чтобы убедиться в крайней нерегулярности их распределения в натуральном ряду, достаточно просто взглянуть на таблицу простых чисел. С одной сторо­ны, встречаются пары простых чисел, отличающиеся друг от друга лишь на две единицы (например, 11 и 13, 17 и 19, 41 и 43). Такие пары простых чисел назы­ваются близнецами. Известны очень большие пары чисел-близнецов; вопрос о том, конечно ли их множество или нет (проблема близнецов), не решен до сих пор. С другой стороны, в натуральном ряду есть сколь угодно длинные промежутки, свободные от простых чисел.

Поэтому уже давно математиков интересовал вопрос о распределении про­стых чисел в натуральном ряду. В XVIII веке новое доказательство бесконеч­ности множества простых чисел было дано членом Петербургской Академии наук, выдающимся математиком своего времени Леонардом Эйлером. В основе этого доказательства лежит формула, которая приведена в 2.1.

Запишем эту формулу в несколько ином виде:

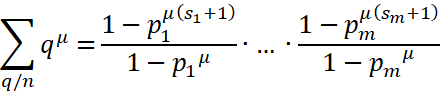, (1)

Где

Устремим показатели к бесконечности. При имеем 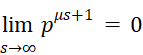, и потому в пределе получим:

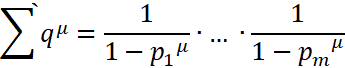, (2)

Тут сумма левой части превратилась в бесконечный ряд, распространенный на все q, в каноническое разложение которых входят лишь числа

Заменяя μ на -t, a q на n, получаем, что при .

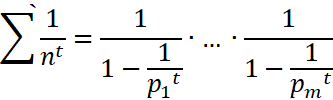, (3)

Где сумма в левой части распространена лишь на числа n вида:

В частности, при имеем:

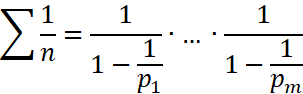, (4)

Если бы множество простых чисел было конечно, например состояло бы лишь из чисел то лишь эти простые числа входили бы в каноническое разложение всех натуральных чисел, и потому левая часть равенства (4) имела бы вид 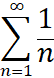. Мы получили бы равенство:

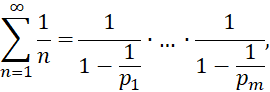
Которое невозможно, поскольку ряд 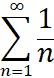(гармонический ряд) расходится, и его сумма не может быть равна никакому числу. Следовательно, такое предположение неверно, и множество простых чисел бесконечно.

Если , то ряд 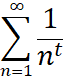сходится. Переходя в равенстве (3) к пределу при , получим:

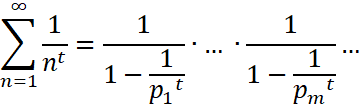, (5)

Где бесконечное произведение распространено на все простые числа Эта замечательная формула Эйлера позволяет преобразовать при ряд 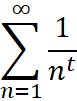в бесконечное произведение, распространенное на все простые числа. Когда , обе части равенства (5) стремятся к бесконечности. Логарифмируя равенство (5), Эйлер вывел, что ряд 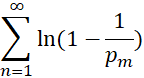расходится, а отсюда нетрудно получить, что расходится и ряд 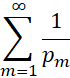, где суммирование ведется по множеству всех простых чисел. Это утверждение означает, что простые числа распространены в натуральном ряду «не слишком редко», что члены вида составляют «весомую часть» в расходящемся гармоническом ряде .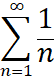

Однако сделать какие-либо точные выводы о распределении простых чисел из расходимости ряда 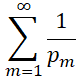невозможно.

2.2. Асимптотический закон распределения простых чисел

Математики конца XVIII и начала XIX века обратились к изучению таблиц простых чисел. Обозначим через (x) количество простых чисел на промежутке [2, x). Поскольку из-за нерегулярности распределения простых чисел явного выражения для (x) получить не удавалось, математики попытались получить асимптотическое приближение для (x). Будем говорить, что функции z=g(x) и z=ψ(x) асимптотически равны при x, если они бесконечно велики при:

x  и 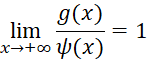. В этом случае пишут g(x)ψ(x).

В 1808 г. французский математик Лежандр опубликовал гипотезу, согласно которой:

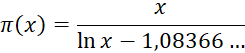
Еще ранее великий немецкий математик К. Гаусс (1777–1855) пришел к предположению, что:

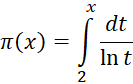
Этот интеграл, называемый интегральным логарифмом, не выражается через элементарные функции. Его обозначают li x.

Однако эти предположения не были доказаны (а гипотеза Гаусса не была и опубликована). Первым после Евклида, кто пошел верным путем в вопросе о распределении простых чисел и достиг важных результатов, был великий русский математик Пафнутий Львович Чебышев (1821–1894). В 1849 г. он доказал, что гипотеза Лежандра ложна и что если при некоторых B и C формула 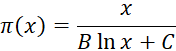верна с точностью до слагаемого порядка  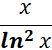, то , . Отсюда вытекает, что, если существует 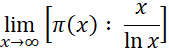, этот предел должен равняться 1.

Утверждение:

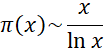
Или равносильное ему утверждение:

Называют асимптотическим законом распределения простых чисел.

П. Л. Чебышев глубоко изучил свойства функции:

,

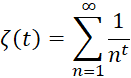Введенной Л. Эйлером. Он получил для этой функции выражение через интегралы и изучил характер ее стремления к бесконечности при .

Получить окончательное доказательство асимптотического закона рас­пределения простых чисел П. Л. Чебышеву не удалось – он не доказал су­ществования предела 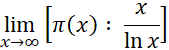. Иной подход к проблеме распределения простых чисел П. Л. Чебышев развил во втором мемуаре о простых числах, появившемся в 1850 г. В нем он доказал, что:

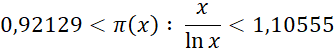
Неравенства Чебышева. Отсюда он вывел следующую теорему, впервые вы­сказанную без доказательства французским математиком Бертраном: между и всегда есть хоть одно простое число.

В 1859 г. немецкий математик Б. Риман изучил функцию не только для действительных, но и для комплексных значений t. Это позволило применить к изучению весьма сильные теоремы, которые были доказаны для функций комплексного переменного. Используя идеи Римана, почти одновременно французский математик Ж. Адамар и бельгийский математик Ш. Валле-Пуссен доказали в 1896 г. асимптотический закон распределения простых чисел.

Основная мысль статьи заключается в том, что правильное применение канонического разложения и свойств числовых функций позволяет эффективно исследовать арифметические свойства натуральных чисел, что является как теоретическим, так и практическим вкладом в области математики.