К вопросу работы ригеля при изгибе со стеснённым кручением

В современном мире широко распространено применение тонкостенных стержней – элементов, у которых три линейных размера величины разных порядков. К таким стержням можно отнести весь сортамент стальных профилей. Напряженно-деформированное состояние балки при чистом изгибе хорошо изучено и формулы для расчёта прочности таких конструкций достаточно точно учитывают напряжения, возникающие в поперечном сечении элемента. Но реальная работа строительных конструкций отличается от идеализированной модели, так как чистый изгиб встречается достаточно редко. Поэтому многие расчёты имеют некоторые допущения в работе. В общем случае при отсутствии возможности искажения плоскости поперченного сечения при изгибе балки появляется стеснённое кручение, что в свою очередь приводит к возникновению, помимо изгибающих моментов, поперечной силы и крутящего момента, бимомента. Бимомент приводит к появлению дополнительных нормальных и касательных напряжений, которые могут как догружать поперечное сечение, так и разгружать его, тем самым давая некий запас прочности.

В свою очередь конструкции из тонкостенных элементов замкнутого сечения мало подвержены воздействию стесненного кручения и поэтому можно пренебречь усилиями, которые возникают в плоскости сечения конструкции. Поэтому в дальнейшем речь будет идти о тонкостенных сечениях открытого профиля, таких как двутавры и швеллеры.

Стоит отметить, что в нашей стране изучали проблематику работы балки при изгибе со стеснённым кручением. Стоит привести основные из них.

В 1905-1906 г. С. П. Тимошенко смог определить экспериментально крутильную жёсткость двутавровой балки и обнаружить возникновение нормальных и касательных напряжений, а уже в 1920 году предложил точный способ нахождения центра изгиба сечения элемента.

1936 – В. З. Власов разработал общую теорию расчёта тонкостенных незамкнутых профилей при кручении с изгибом. Он смог доказать, что закон плоских сечений – это частный случай закона секториальных площадей. Его труд позволил сформировать более понятную методику определения нормальных и касательных напряжений в поперечном сечении элемента.

1940 г. – выходит книга В. З. Власова «Тонкостенные упругие стержни».

1962 г. – издание книги Д. В. Бычкова «Строительная механика стержневых тонкостенных конструкций». В этом труде приведены методики и примеры расчёта балочных тонкостенных систем. Это первый справочник для проектировщиков, в котором указаны примеры расчёта при стеснённом кручении.

2011 г. – выход СП 16.13330.2011 «Стальные конструкции», где введена формула для расчёта стальных конструкций с учётом бимомента.

Таким образом данная проблема широко изучена в нашей стране и разработана методика расчёта реальных конструкций.

В тонкостенных стержнях не всегда применим принцип Сен-Венана и гипотеза плоских сечений. Вследствие этого наблюдается депланация поперечного сечения стержня – перемещение точек сечения в направлении продольной оси стержня. На неё влияет условие закрепления, если депланация не одинакова в разных поперечных сечениях, то такое деформирование называют стеснённым кручением. В свою очередь депланация приводит к возникновению бимомента, который можно представить в виде противоположно направленных моментов, находящихся на определенном расстоянии друг от друга (рис. 1.)

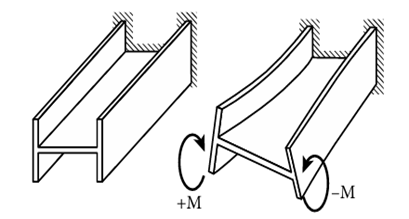
Рис. 1. Действие бимомента

Поэтому для возможности учёта стеснённого кручения используют теорию Власова В. З., которая использует следующие допущения:

• по толщине нормальные напряжения распределены равномерно;
• продольные волокна не давят друг на друга;
• контур поперечного сечения не деформируется (рис. 2).

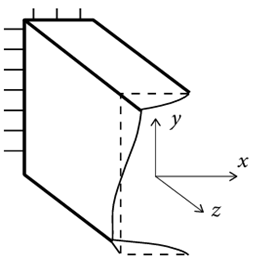
Рис. 2. Депланация сечения

Поэтому формула для стесненного кручения с изгибом, когда не работает гипотеза плоских сечений, примет вид:

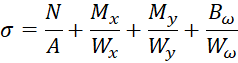, (1)

В свою очередь:

, (2)

Где:

– бимомент, кН м²;

– секториальный момент инерции;

– секториальный момент сопротивления;

– секторальная координата.

В общем виде исходя из принципа суперпозиции силу, приложенную с эксцентриситетом в двух направлениях, можно разложить на 4 варианта, которые влияют на 4 усилия (продольная сила, моменты в двух плоскостях и бимомент (рис. 3)):

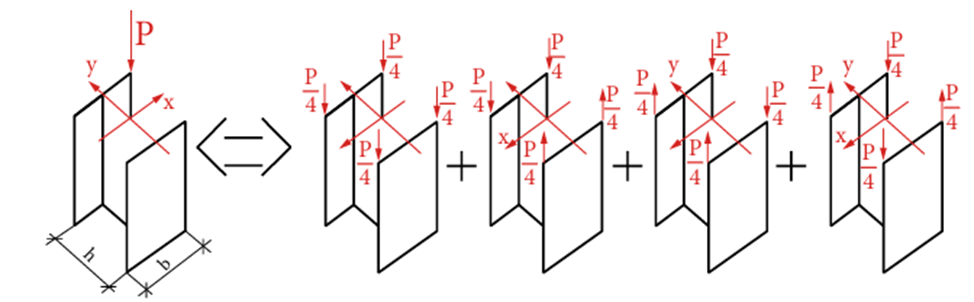
Рис. 3. Разложение силы с эксцентриситетом по правилу суперпозиции

Но данная формула предполагает упругую работу материала, что предполагает завышенное значение поперечного сечения. Как показывают натурные испытания, максимально приближённые к реальной работе с учётом пластических деформаций прочность двутавровой балки повышается примерно на 19%. При этом потеря несущей способности всё равно наступает раньше, чем у балки, работающей только на изгиб. Это связано с дополнительными секторальными напряжениями, которые суммируются с нормальными напряжениями от изгиба.

По результатам экспериментов установлено, что текучесть наступает в первую очередь в местах сечения, где напряжения бимомента и изгибающего момента сонаправлены. Примечательно, что дальнейшее развитие пластических деформаций, после начала текучести в некоторых местах полки двутавра сопровождается малыми отклонениями углов поворота сечения от упругих значений. Но с началом текучести по всей ширине полки и образованием пластического шарнира происходит потеря несущей способности балки. Получается, что развитие пластических деформаций в некоторых участках поперечного сечения элемента не гарантируют скорую потерю несущей способности элемента. Кроме того, разные по знакам напряжения разгружают части элемента. При определении дополнительных напряжений от стесненного кручения требуется учитывать вид закрепления стержня по концам. При работе балки в составе рамы следует учитывать жесткость узлов и податливость колонны, к которой она закреплена.

Резюмируя всё вышесказанное можно сказать, что влияние бимомента при изгибе со стеснённым кручением может быть существенным и сильно влияет на несущую способность конструкции. Возможность численного расчёта резервов прочности с учетом пластических деформаций является актуальной задачей, которая требует дополнительных исследований. Пренебрежение учета бимомента в строительных конструкциях чревато чрезвычайными ситуациями в процессе эксплуатации.