В начале, следует отметить, что мы ничего не придумываем того, чтобы фактически не было бы использовано физиками в том или ином виде. Мы просто показываем логику связи явлений, что уже нашло как теоретическое, так и практическое применение в физике. Различие нашей теории Мироздания с общепринятой теорией физиков в том, что они использовали чудодейственное возникновение и исчезновение придуманных ими частиц, таких как виртуальные фотоны, гравитоны, кварки и глюоны с отсутствием математического взаимодействия и возникновением их из вакуума. На этом основан принцип взаимодействия через телепортацию, что отрицает необходимость наличия самих законов физики и, следовательно, развивать в физике стало нечего. Мы же опираемся на закон Ломоносова М. В., по которому объекты состоят из того, на что они распадаются.
Исходя из этого понятно, что первым основополагающим явлением, в объективной реальности, является взаимодействие противоположностей в любом существующем объекте Мироздания. Это явление получило название корпускулярно-волнового дуализма. В философии это было обозначено в виде закона единства и борьбы противоположностей [1, с. 5-37]. Логика такого явления объясняется довольно просто: исходя из противоречий, от обратного. Действительно, как можно выявить существование отдельного объекта, если отсутствие противоположностей означает однородность? Да, никак! Однако определив необходимость наличия противоположностей в Мироздании, мы должны определить их взаимодействие. В противном случае скатываемся вновь к наличию не одной, а нескольких однородностей, которые имеют независимое существование в наших фантазиях. Отсюда следует требование обязательного взаимодействия противоположностей. Это взаимодействие может быть связано только с взаимным преобразованием объектов одной противоположности в объекты другой противоположности, и наоборот. В противном случае мы приходим к чудесам возникновения из ничего и исчезновения в ноль, и здесь, собственно, нет и самого взаимодействия, так как нет взаимного влияния через изменения. Отсюда сам принцип взаимодействия с преобразованием математически основан на увеличении объектов первой противоположности (сложение) за счёт уменьшения объектов второй противоположности (вычитание), и наоборот. Другого способа взаимодействия в принципе не существует, так как иное исключает влияние через изменения. Соответственно при наличии влияния через количественные изменения (это связано со скоростью обмена) стоит вопрос о необходимости равенства перехода объектов по количеству из одной противоположности в другую противоположность, так как иное приводит к исчезновению одной из противоположностей. Иными словами, различие противоположностей на основе неравенства количества приводит к чудесам возникновения из нуля, или исчезновение в ноль. Такое равное преобразование противоположностей означает их замкнутое взаимодействие. Понятно, что мы также должны дать характеристику различия противоположностей с точки зрения описания самих объектов этих противоположностей. Однако как это представить с точки зрения математики? Если исходить из количественной оценки, то здесь различий противоположностей быть не может, так как обмен между противоположностями равный. Отсюда остаётся единственный вариант отличия противоположностей с точки зрения математики через влияние противоположностей друг на друга, что выражается в переходе объектов через операции сложения и вычитания, которые являются основополагающими для различия любых закономерностей. Соответственно, операция сложения объектов в одной противоположности выглядит вычитанием в другой противоположности, и наоборот. Иными словами, различие объектов по существованию в противоположностях основано на рассмотрении процессов взаимодействия от системы наблюдения в зависимости от противоположности. Однако, если рассматривать процессы взаимодействия противоположностей по математике только с точки зрения обычного количественного сложения и вычитания, то мы будем иметь превращение противоположностей в однородность одной противоположности. Это говорит о том, что для соблюдения вечного существования противоположностей в Мироздании необходимо наличие более сложных закономерностей, которые обеспечивали равенство операций сложения и вычитания. Необходимость замкнутости глобальных противоположностей друг на друга, для избегания чудес, требует равного количественного преобразования, а это означает, что действие равно противодействию. Отсюда воздействие первой противоположности на вторую связано с ответной реакцией, что выражается в исключении влияния первой противоположности через отрицание со знаком минус. Соответственно вычитание в одной глобальной противоположности рассматривается как сложение в другой глобальной противоположности, так как иначе нет отличий между противоположностями из-за различий по закономерностям. Отсюда единственным атрибутом отличия объектов в противоположностях с точки зрения математики и логики является мнимая единица i=(‒1)1/2, которая обеспечивает отрицание при возврате в начальную противоположность со знаком минус. Ничего другого без чудес придумать невозможно. Более подробно мы это рассмотрели в [1, с. 5-37], в результате чего была выведена общая формула Мироздания:
| (1) |
Здесь ![]() , в этом случае аргументы имеют равенство по количеству. При этом мы имеем различие противоположностей на основе атрибута в виде мнимой единицы, что даёт смену закономерностей в зависимости от системы наблюдения. Понятно, что наша логика законов должна соответствовать практике замкнутых законов преобразования в физике. Поэтому посмотрим, какое соответствие имеет выведенный нами закон (1) с теорией относительности Эйнштейна. Для показа этого мы сделаем следующие преобразования СТО Эйнштейна в замкнутом виде [2, с. 213]:
, в этом случае аргументы имеют равенство по количеству. При этом мы имеем различие противоположностей на основе атрибута в виде мнимой единицы, что даёт смену закономерностей в зависимости от системы наблюдения. Понятно, что наша логика законов должна соответствовать практике замкнутых законов преобразования в физике. Поэтому посмотрим, какое соответствие имеет выведенный нами закон (1) с теорией относительности Эйнштейна. Для показа этого мы сделаем следующие преобразования СТО Эйнштейна в замкнутом виде [2, с. 213]:
| (2) |
Последнее уравнение в (2) будет соответствовать уравнению (1), если vx=c, и при этом для достижения равенства на основе нашей логики используются закономерности. Иными словами, общий закон Мироздания в СТО Эйнштейна обеспечивается при связи систем наблюдения через скорость света (скорость обмена). Собственно, в таком подходе мы не являемся первопроходцами, так как впервые связь СТО и ОТО Эйнштейна с гиперболическими косинусами и синусами, а также и с обычными косинусами и синусами показал ещё Минковский [3, с. 226]. Выясним теперь, что представляют собой в геометрии Минковского преобразования Лоренца. Здесь, соответственно вводятся обозначения:
![]() , (3)
, (3)
При этом полагается:
![]() , (4)
, (4)
Запишем преобразования Лоренца, отвечающие движению системы отсчёта вдоль оси Х1 по рисунку 1 в следующем виде:
| (5) |
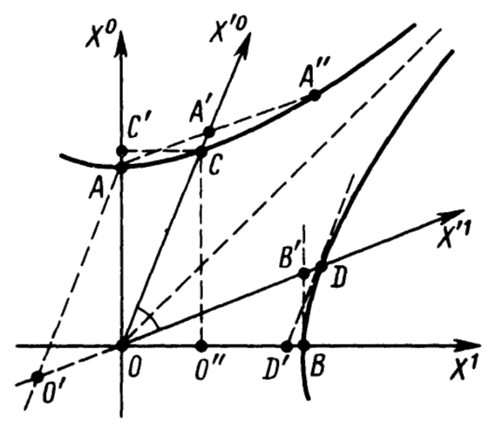
Рис. 1. Геометрия Минковского
Здесь учитывается, что:
![]() , (6)
, (6)
Очевидно, преобразования (5) представляют собой переход от прямоугольной системы координат к косоугольной с дополнительным растяжением. При таком переходе каждая точка плоскости занимает некоторое положение на соответствующей ей гиперболе с выполнением равенства:
![]() , (7)
, (7)
Далее учитываем, что:
| (8) |
Отсюда гиперболический поворот можно представить в виде поворота на мнимый угол ![]() , где
, где ![]() :
:
| (9) |
Таким образом, роль окружностей за счёт поворота на мнимый угол (действительный в другой противоположности) в псевдоевклидовой геометрии Минковского играют гиперболы. Иными словами, Минковский ещё до нас математически связал интуитивно сложение и вычитание, но не понял, что это означает связь глобальных противоположностей.
Чтобы обосновать представление последнего уравнения (2) через закономерности по геометрии Минковского, мы должны учесть:
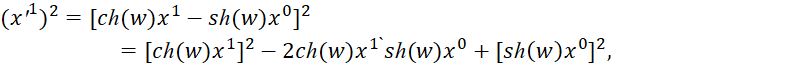 | (10) |
Отсюда мы видим, что при вычитании имеем инвариантную форму:
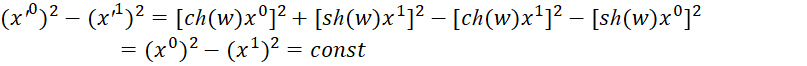 , (11)
, (11)
Учитывая, что данная форма на основе закона сохранения количества для каждого объекта остается инвариантной в полученной нами системе, следует вывод: сумма данных форм от всех объектов также будет равна константе, а значит, может быть приведена к единичному уровню.
Также учитывая, что для выполнения СТО Эйнштейна требуется необходимость соблюдения тождества последнего уравнения в (2) следует условие представления любого объекта Мироздания как закономерности, зависящей от количественного значения в аргументе функции с учётом атрибута принадлежности к системе наблюдения соответствующей противоположности. Собственно, получили выполнение философского закона перехода количества в новое качество. Это происходит в силу изменения воздействий для выполнения закона сохранения количества между противоположностями, при сложении в одной противоположности и вычитании в другой противоположности. Иначе, в противном случае, не обеспечить закон сохранения количества между противоположностями, что означает исчезновение одной из них с переходом к однородности. Отсюда, можно прийти к следующему выводу: если сумма значений всех объектов по координате ![]() соответствует ch(w), а по координате
соответствует ch(w), а по координате ![]() равна sh(w), так как иначе не будет замкнутой системы Мироздания с учётом инвариантной формы, то в этом случае сразу приходим к инвариантной нормированной к единице форме:
равна sh(w), так как иначе не будет замкнутой системы Мироздания с учётом инвариантной формы, то в этом случае сразу приходим к инвариантной нормированной к единице форме:
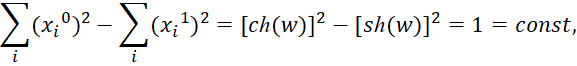 | (12) |
Если учесть соотношения (5) и (9) с наличием смены принадлежности аргумента за счёт наблюдения из противоположной системы со сменой вычитания на сложение при ![]() , то в противоположной системе наблюдения получим соотношение:
, то в противоположной системе наблюдения получим соотношение:
![]() , (13)
, (13)
Таким образом, логику формулы (1) в соответствии с СТО и ОТО Эйнштейна фактически показал Минковский, только он так же, как и другие физики не учёл наличие представления объектов в зависимости от системы наблюдения, исходя из наличия противоположностей в каждом объекте. Минковский фактически представил переход от преобразований Лоренца через гиперболический косинус и синус к уравнению окружности с заменой за счёт мнимой единицы закономерностей, что, собственно, и позволяет получить тождество по формуле Мироздания (1). Однако он не понял, что, заменив вещественное значение аргумента у функций на то же вещественное значение аргумента, но с атрибутом в виде мнимой единицы, он тем самым поменял систему наблюдения.
Отметим, что представление объектов в зависимости от системы отсчёта (наблюдения) ввёл ещё Эйнштейн, так как в зависимости от системы отсчёта один и тот же объект может рассматриваться с различной энергией. Разница лишь в том, что мы основываемся на факте связи глобальных противоположностей через скорость света. Аналогичный вывод о зависимости от системы наблюдения следовал и из наличия помимо СТО Эйнштейна из ОТО Эйнштейна, так как в ОТО пространственно-временное искривление рассматривалось относительно скорости, которое реально не наблюдалось в системе отсчёта для скорости в СТО. При этом, как в СТО, так и в ОТО, рассматривалось наличие пространственно-временного искривления в зависимости от скорости. Замкнутость Мироздания на противоположности означает симметрию в выполнении законов физики, а это означает, что мы иначе, чем через скорость представить пространственно-временное искривление не можем. Но если это значение скорости по ОТО не наблюдается в пространстве через проекции по координатам длины, то остаётся единственный вариант, что эта скорость по ОТО выражается в проекции на время. Так как длина и время в противоположностях меняются местами из-за скорости обмена (скорости света), то длина переходит во время, а время переходит в длину, и это уже обозначает скорость от временной проекции в противоположности как реальную величину по координатам длины. Таким образом, единственным выходом из указанного парадокса между СТО и ОТО Эйнштейна является логическое умозаключение, что представление о скорости меняется в зависимости от системы наблюдения в противоположностях. Тогда с учётом перехода на практике корпускулярных свойств в волновые свойства, например, при аннигиляции позитрона и электрона, а также при переходе фотона при столкновении с электроном в дополнительную пару электрона и позитрона, мы сделали вывод, что в противоположностях корпускулярные свойства переходят в волновые свойства, и наоборот. А это означает переход потенциальной энергии в кинетическую энергию, и наоборот. Собственно иного способа взаимосвязи противоположностей попросту нет, так, как если бы при переходе от одной системы наблюдения к другой системе наблюдения не было бы изменений корпускулярных свойств на волновые свойства, и наоборот, то говорить о противоположностях и о корпускулярно-волновом дуализме было бы невозможно. Как говорится, если нет изменений, то, значит, нет и отличий, и мы имеем однородность.
Далее отметим, что вариант, представленный в последнем уравнении (2), соответствует частному случаю движения некоторого объекта со скоростью vx. Однако при сохранении самого объекта этот вариант также должен подчиняться общему закону Мироздания, иначе распад объекта. Для исключения распада объекта должно быть его такое взаимодействие с окружающей средой (ничего другого для взаимодействия и нет) при котором существует равноценный обмен. Отсюда в (2) на основе величины vx/с, мы имеем для сохранения движущегося объекта взаимодействие через окружающую среду. Как это будет показано несколько ниже, окружающая среда характеризуется константами электрической и магнитной проницаемости, которые определяются интегральным движением в противоположности с выполнением условия термодинамического равновесия по формуле Планка. Повторим, что иного способа взаимодействия объекта, минуя окружающую среду, не существует. Понятно, что физики тоже не смогли обойти взаимодействия с окружающей средой, но, как всегда, пошли по пути чудес, придумав электромагнитный и электронно-позитронный вакуум.
Далее мы замечаем, что наличие ограничения в скорость света в СТО Эйнштейна у многих физиков также вызывает сомнение, поэтому была выдвинута гипотеза существования тахионов [4, с. 291], частиц, которые движутся со скоростью выше скорости света. Однако физики явно забыли, что, например, бесконечная скорость света (обмена, изменения) означает с точки зрения замкнутой системы на две глобальные противоположности мгновенный ответ действия на противодействие, что исключает изменение объектов во времени. Иными словами, самой теории относительности, с выполнением аналогичных законов физики в разных системах отсчёта по СТО Эйнштейна, в этом случае в принципе быть не может. Понятно, что и нулевое значение скорости света означает отсутствие взаимодействия. Отсюда требование наличия скорости света как константы, так как в противном случае инвариантной формы в разных системах отсчёта не получить и будет вариант, когда объект в одной системе отсчёта должен сохраняться, а в другой системе отсчёта он будет иметь, например, распад, что на практике не наблюдается.
Замкнутость Мироздания на две глобальные противоположности определяет её равенство константе (в противном случае чудеса). И если Мироздание является константой, то обмен между глобальными противоположностями может проходить только с одной постоянной скоростью с исключением значения бесконечности и нуля. Иначе мироздание автоматически становится закономерностью и, соответственно, не может быть замкнутой величиной. Понятно, что эта константа в скорость света не может меняться в зависимости от системы отсчёта и при переходе в противоположность, так как в этом случае возникает неравенство на величину отличия и это подразумевало бы иные законы взаимодействия, что противоречит симметрии противоположностей на основе закона сохранения количества. Наличие количества, связанного с дискретностью в виде элементарных объектов, определяется необходимостью взаимодействия через обмен между двумя глобальными противоположностями. Если нет реальных дискретных объектов (что определяется в виде количества в математике), то и обмениваться нечем, и нет взаимодействия, а значит, нет существования противоположностей. Поэтому в физике ограничение шага дискретизации константой постоянной Планка исключает полную однородность, которая была бы в случае значения постоянной Планка равной нулю и тогда противоположности в принципе бы не существовали. При этом, необходимость константы в виде постоянной Планка (h) связывают с отсутствием «ультрафиолетовой катастрофы» и ростом энергии, а значит и ростом количества до бесконечности. При замкнутости Мироздания на две глобальные противоположности шаг дискретизации тоже автоматически следует из постоянства скорости обмена. То есть, определить скорость обмена для бесконечно малого объекта не представляется возможным. Отсюда следует известный парадокс математики, при котором быстроногий Ахиллес, при отображении движения через приращения дискретных величин практически до нуля, никогда не догонит неторопливую черепаху, если в начале движения черепаха находится впереди Ахиллеса.
Так, задавшись величиной минимального объекта Nнач, и определив его скорость передачи (обмена, изменения) как S, мы при наличии бесконечно малых объектов другой величины всегда можем представить этот объект как Nнач=kn, где n ‒ это еще меньший по величине объект. Соответственно, скорость передачи s для отдельного объекта n должна быть выше в k раз, чтобы обеспечить взаимодействие со всеми объектами, так как в противном случае получаются объекты без взаимодействия, а значит, их и нет в мироздании. В этом случае при стремлении шага величины дискретизации к нулю нет и предела скорости обмена, которая вырастает до бесконечности. Это противоречит физике необходимости связи длины и времени по СТО и ОТО Эйнштейна с наличием пространственно-временного континуума и приводит к геометрии Эвклида с независимостью координат длины и времени, что исключает и наличие самих объектов. При этом мы напоминаем, что любые изменения у нас связаны с переходом в противоположность, поэтому вариант с движением в одной противоположности, например движение поезда, здесь не подходит, так как в этом случае рассматривается вариант без взаимодействия с противоположностью, то есть отрицается необходимость самих противоположностей. Понятно, что возникает также вопрос о возможности смены значений констант на другие величины, однако он также отпадает в силу того, что глобальные противоположности в мироздании также существуют вечно и их отличие определяется только закономерностями в зависимости от системы наблюдения при сохранении количества, что будет показано несколько ниже.
Отсюда вывод: замкнутость Мироздания на две глобальные противоположности определяет как константы, и значение максимальной скорости обмена (света) и значение минимального шага дискретизации для элементарных объектов, что требует наличие единичных объектов воздействия. При этом константа Мироздания определяется величиной произведения скорости обмена на шаг дискретизации с равенством единице.
В противном случае были бы единичные элементы, которые не участвуют в обмене, а значит, независимы от процессов в мироздании. Такая независимость означает отсутствие взаимодействия, а взаимодействие означает обмен. Поэтому, если единичный объект не принимает участие в обмене, то он и не взаимодействует, и значит, независим. Но участие в обмене определяется скоростью. Поэтому скорость обмена должна быть такова, чтобы изменению подверглись все единичные элементы мироздания. А иначе неохваченные элементы автоматически становятся независимыми.
Отсюда получаем: произведение скорости света (с) на величину постоянной Планка (h) определяет значение константы нашего мироздания по взаимодействию:
![]() , (14)
, (14)
Данная формула для констант аналогична требованию инвариантности по формуле, полученной из преобразований Лоренца в СТО Эйнштейна с наличием обратно-пропорциональной связи в динамике взаимодействия, где в качестве противоположностей выступают длина и время:
![]() , (15)
, (15)
Здесь мы имеем следующую логическую цепочку. Замкнутость мироздания определяет постоянство скорости обмена при взаимодействии, что приводит и к наличию минимального шага дискретизации. Так как взаимодействие возможно только в случае обмена, то исключить независимость отдельных элементов можно только тогда, когда общий количественный обмен, который и характеризует энергию взаимодействия, определяется по формуле произведения скорости света и постоянной Планка!
Понятно, что данные утверждения должны соответствовать формулам для физических явлений, поэтому отметим, что необходимость связи скорости света с постоянной Планка уже была введена до нас в физике как постоянная тонкой структуры [5, с. 341]:
![]() , (16)
, (16)
Разница лишь в нормировке связанная с системой измерения. Её можно пересчитать, если учесть, что заряд q по теории Дирака [6, с. 349] можно считать равным плюс или минус единице, так как заряда нет в формуле энергии Эйнштейна, и его роль сводится к представлению операции излучения или поглощения, то есть не количества, а действия – закономерности. Отсутствие значения заряда в формуле энергии Эйнштейна означает и отсутствие у заряда силового воздействия, так как нет энергии для этого. Ещё раз отметим, что придумать иной принцип взаимодействия помимо обмена − невозможно, а обмен обязательно характеризуется скоростью и величиной шага дискретизации. Собственно, и физики не смогли обойтись без взаимодействия, но придумали для этого виртуальные фотоны и гравитоны. Помимо этого, надо ещё раз отметить, что произведение скорости обмена (света) на шаг дискретизации (постоянная Планка) имеет значение, равное единице, в противном случае либо скорость обмена, либо шаг дискретизации имеют иную величину. Одновременно из формулы (14) следует необходимость и ограничение числа объектов в Мироздании по формуле:
![]() , (17)
, (17)
Фактически это означает, что ни один объект не может войти или выйти из замкнутой на две глобальные противоположности системы Мироздания.
Понятно, что замкнутая система Мироздания и определяет законы физики. Поэтому покажем, как на основе закона окружности получается известная формула энергии Эйнштейна. Отсюда при условии сохранения объекта (замкнутая система обмена) динамика взаимодействия противоположных частей объекта, с учётом наблюдения из одной выбранной противоположности, будет выглядеть с учётом максимальной скорости обмена в виде:
![]() , (18)
, (18)
Перепишем полученное уравнение с учётом переноса:
![]() , (19)
, (19)
Далее произведем следующие преобразования:
| (20) |
Последнее уравнение по виду аналогично уравнению преобразований Лоренца. И отсюда мы также можем получить соответствие с уравнением энергии Эйнштейна, если сделать замену переменных и считать, что m=1/v1, а m0=1/c. В итоге имеем:
| (21) |
Если умножить оба члена указанного последнего уравнения на одинаковую величину c2=с/h=Nоб, то получим формулу энергии Эйнштейна в виде ![]() . Значение Nоб определяет общее количество элементарных объектов в мироздании при обмене и их взаимосвязи через скорость света. Соответственно мы видим, что энергия и масса выступают как противоположности, связанные обратно-пропорциональной связью, и фактически они заменяют соотношение неопределённостей Гейзенберга в детерминированном виде. Можно представить энергию Эйнштейна и в ином виде:
. Значение Nоб определяет общее количество элементарных объектов в мироздании при обмене и их взаимосвязи через скорость света. Соответственно мы видим, что энергия и масса выступают как противоположности, связанные обратно-пропорциональной связью, и фактически они заменяют соотношение неопределённостей Гейзенберга в детерминированном виде. Можно представить энергию Эйнштейна и в ином виде:
| (22) |
Это означает, что из преобразований Лоренца, которые тоже связаны с формулой окружности, получается и уравнение энергии Эйнштейна. Учитывая, что в формулу Эйнштейна входят только две переменные величины, которые дают замкнутую систему по формуле окружности, то они и являются противоположностями друг для друга (аналогично длине и времени, которые связаны через скорость света, что было впервые сделано Минковским в [3, с. 226]), то есть могут преобразовываться только друг в друга. Отсюда следует, что указанные величины как противоположности не могут выражаться через один и тот же вид. Иначе такое преобразование ничем не зафиксировать в силу отсутствия различий между противоположностями. Однозначная связь скорости света и величины постоянной Планка, в виде ch=1, с учётом требования смены представления объектов в противоположных системах наблюдения, означает необходимость записи переменных в виде m0=h=1/с. То есть минимальная масса определяется минимально возможной величиной постоянной Планка, и эта величина должна выражаться в виде значения одной из противоположностей. В противном случае была бы независимость от обмена. Повторим, что аналогичный вариант, из-за однозначной связи также следует из предложения физиков в системе измерения СИ в виде постоянной тонкой структуры ![]() . Однако, в варианте физиков нарушается необходимость взаимодействия с охватом всех частиц Мироздания через значение скорости обмена (скорости света). Таким образом, мы элементарную минимальную массу объекта представляем в виде величины, связанной с величиной постоянной Планка, так как Мироздание оперирует в реальности количеством в виде объектов минимальной величины и закономерностями. То есть Мироздание ничего не знает о системах измерения массы (например, в килограммах), придуманных людьми. Отметим, что системы измерения, придуманные людьми, приводят к парадоксам в виде чёрных дыр (система измерения СИ) и обоснования вакуума как пустоты, подчинённой геометрии Эвклида (система измерения СГС, где в классических уравнениях Максвелла исключаются константы электрической и магнитной проницаемости для характеристики пространства и времени как объектов). Выбор дискретной величины для массы покоя равной постоянной Планка означает, что электрон и позитрон ‒ это минимальные дискретные корпускулярные объекты и их изменение связано только с переходом в противоположность в результате аннигиляции, а не распада на ещё более мелкие корпускулярные объекты. Соответственно в системе Мироздания, если одна переменная величина выражает скорость v, то второй изменяемой переменной остаётся роль массы и при этом v1=1/m. В противном случае определить наличие противоположностей невозможно, если вид объектов в противоположностях сохраняется. Так как операция сложения при инвариантной форме, за счёт переноса значения v2, из левой части уравнения (18) от знака равенства в правую часть от знака равенства в (19), приводит к смене суммы на разность, то для соблюдения инвариантной формы в виде тождества необходимо сменить и закономерности. В противном случае в математике возникают решения с делением на ноль и бесконечными значениями. Именно этим логика физики отличается от логики математики. Другими словами, мы переходим из рассмотрения процесса в волновом виде к корпускулярному виду, и сложение в одной противоположности должно отображаться вычитанием в другой противоположности. Таким образом, замкнутые преобразования по СТО Эйнштейна требуют наличия разных систем наблюдения от длины и времени с переходом этих величин друг в друга в зависимости от системы наблюдения и сменой закономерностей.
. Однако, в варианте физиков нарушается необходимость взаимодействия с охватом всех частиц Мироздания через значение скорости обмена (скорости света). Таким образом, мы элементарную минимальную массу объекта представляем в виде величины, связанной с величиной постоянной Планка, так как Мироздание оперирует в реальности количеством в виде объектов минимальной величины и закономерностями. То есть Мироздание ничего не знает о системах измерения массы (например, в килограммах), придуманных людьми. Отметим, что системы измерения, придуманные людьми, приводят к парадоксам в виде чёрных дыр (система измерения СИ) и обоснования вакуума как пустоты, подчинённой геометрии Эвклида (система измерения СГС, где в классических уравнениях Максвелла исключаются константы электрической и магнитной проницаемости для характеристики пространства и времени как объектов). Выбор дискретной величины для массы покоя равной постоянной Планка означает, что электрон и позитрон ‒ это минимальные дискретные корпускулярные объекты и их изменение связано только с переходом в противоположность в результате аннигиляции, а не распада на ещё более мелкие корпускулярные объекты. Соответственно в системе Мироздания, если одна переменная величина выражает скорость v, то второй изменяемой переменной остаётся роль массы и при этом v1=1/m. В противном случае определить наличие противоположностей невозможно, если вид объектов в противоположностях сохраняется. Так как операция сложения при инвариантной форме, за счёт переноса значения v2, из левой части уравнения (18) от знака равенства в правую часть от знака равенства в (19), приводит к смене суммы на разность, то для соблюдения инвариантной формы в виде тождества необходимо сменить и закономерности. В противном случае в математике возникают решения с делением на ноль и бесконечными значениями. Именно этим логика физики отличается от логики математики. Другими словами, мы переходим из рассмотрения процесса в волновом виде к корпускулярному виду, и сложение в одной противоположности должно отображаться вычитанием в другой противоположности. Таким образом, замкнутые преобразования по СТО Эйнштейна требуют наличия разных систем наблюдения от длины и времени с переходом этих величин друг в друга в зависимости от системы наблюдения и сменой закономерностей.
Надо отметить, что использование при математических расчётах смены системы наблюдения применил интуитивно и Бор при вычислении радиуса движения электрона по орбите вокруг протона. При этом он использовал уравнение гармонического осциллятора, которое (при нормировке на ![]() ) отражает уравнение окружности в виде [7, с. 58-59].
) отражает уравнение окружности в виде [7, с. 58-59].
![]() , (23)
, (23)
Суть необходимости использования уравнения гармонического осциллятора для объяснения взаимодействия противоположностей с наличием частоты излучения мы покажем несколько ниже. Из (23) Бор получил формулы вида:
| (24) |
При определении первой орбиты водорода Бор фактически использовал смену системы наблюдения за счёт формулы ![]() при замене импульса на радиус орбиты. Иными словами, он сделал пересчёт кинетической энергии в потенциальную энергию пространственного искривления и тем самым фактически сменил систему наблюдения на противоположную систему с учётом связи через скорость света (при соответствующей нормировке на
при замене импульса на радиус орбиты. Иными словами, он сделал пересчёт кинетической энергии в потенциальную энергию пространственного искривления и тем самым фактически сменил систему наблюдения на противоположную систему с учётом связи через скорость света (при соответствующей нормировке на ![]() ). Отсюда Бор получил уравнение:
). Отсюда Бор получил уравнение:
| (25) |
Однако парадокс, допущенный Бором в том, что своим постулатом по дискретным орбитам он исключил излучение при движении электрона на дискретных орбитах, в то время как уравнение гармонического осциллятора именно основано на излучении, в виде значения ![]() .
.
Отметим, что с учётом нашей теории разница на ![]() , не позволяет представить длину и скорость как противоположности с учётом условия охвата всех объектов Мироздания при взаимодействии. Величина радиуса характеризует систему наблюдение процесса, но не определяет взаимодействие в преобразовании величин. При этом использование радиуса при взаимодействии приводит к парадоксам, как, например, магнитная сила при движении заряда по окружности не может осуществлять работы [8, с. 118-119]. Однако это означает существование силы без затрат энергии по второму закону Ньютона, чего быть не может. Иными словами, использовать неизменное значение радиуса как константы для описания динамики взаимодействия сил нельзя. Отсюда правильная нормировка в динамике взаимодействия соответствует не радиусу, а длине окружности, по которой осуществляется взаимодействие с учётом формул:
, не позволяет представить длину и скорость как противоположности с учётом условия охвата всех объектов Мироздания при взаимодействии. Величина радиуса характеризует систему наблюдение процесса, но не определяет взаимодействие в преобразовании величин. При этом использование радиуса при взаимодействии приводит к парадоксам, как, например, магнитная сила при движении заряда по окружности не может осуществлять работы [8, с. 118-119]. Однако это означает существование силы без затрат энергии по второму закону Ньютона, чего быть не может. Иными словами, использовать неизменное значение радиуса как константы для описания динамики взаимодействия сил нельзя. Отсюда правильная нормировка в динамике взаимодействия соответствует не радиусу, а длине окружности, по которой осуществляется взаимодействие с учётом формул:
| (26) |
В результате изменения по скорости и длине с учётом систем наблюдения и обратно-пропорциональной связи равны. Отсюда никаких нормировочных коэффициентов в этом случае не требуется. Следует отметить, что, так как в среде распространения значение длины окружности отражается через пространственно-временное искривление, так как в противном случае мы имеем геометрию Эвклида без возможности связи по координатам, то в противоположной системе наблюдения это значение играет роль массы, и мы можем записать r=m=1/v. Это означает, что скорость в одной системе наблюдения представляется значением массы (длины, отражающей пространственное искривление) в противоположной системе наблюдения. Действительно, если рассматривать массу как нечто отдельное от пространственно-временного искривления, то надо придумать механизм (закон) влияния этой массы на изменение пространственно-временное искривление, а его как раз и нет. Следовательно, мы расширили замену, введённую Бором исходя из того, что массы как таковой вне описания пространственно-временного искривления по СТО и ОТО Эйнштейна не существует. Повторим, что в современной физике сейчас господствует представление, что масса ‒ это нечто отдельное и отсюда возможна некая нейтральная масса внутри пространственно-временного искривления среды распространения. При этом придумано даже отдельное взаимодействие через гравитоны. О парадоксах, которые при этом имеют место, мы говорили в [9, с. 5-44].
Далее необходимо вспомнить саму формулу Луи де Бройля [10, с. 63] отражающую корпускулярно-волновой дуализм:
![]() , (27)
, (27)
Как мы не раз показывали, эта формула выводится из аргумента волновой функции ![]() , которая отражает условие, где количественные изменения в аргументах функций в противоположностях равны:
, которая отражает условие, где количественные изменения в аргументах функций в противоположностях равны:
| (28) |
С учётом нашей теории для элементарной частицы с массой m0=1/c мы можем связать частоту и скорость в виде:
| (29) |
Здесь необходимо отметить, что представление через частоту и скорость относится к противоположным системам наблюдения, связанным через скорость света. Иными словами, мы имеем первоначальную связь через скорость света аналогично связи длины и времени по идее Минковского [3, с. 226]. Из формулы (29) также следует, что представление процесса и физических величин также зависит от системы наблюдения. Теперь вспомним известную формулу Луи де Бройля для описания «волн материи» по которой со всякой неподвижной частицей массой m связан некоторый периодический процесс частоты ![]() [11, с. 216] и учтём ОТО Эйнштейна, а также что по нашей теории m0=1/c=h:
[11, с. 216] и учтём ОТО Эйнштейна, а также что по нашей теории m0=1/c=h:
| (30) |
Таким образом, мы вновь приходим к уравнению окружности, то есть замкнутой системы на две противоположности, где в общей системе наблюдения скорости от противоположностей выражаются в обратно-пропорциональной зависимости. Как будет показано несколько ниже, такой же вид получается и в случае взаимодействия электрических и магнитных составляющих, что говорит о симметрии законов в противоположностях.
Таким образом, из нашей теории Мироздания следуют законы физики, которые показывают связь скорости, массы, частоты исходя из наличия противоположностей, замкнутых друг на друга с наличием обмена между ними. Собственно, чтобы оправдать связь массы покоя с частотой, Луи де Бройль постулировал существование волнового поля:
![]() , (31)
, (31)
Не зная, что собой физически представляет это волновое поле, физики стали интерпретировать его как функцию, которая характеризует вероятность. Но мы отметим, что при эксперименте Дэвиссона и Джермера [10, с. 63] с однозначно получаемой верхней формулой (29), случайностей нет, так как при случайностях величины в опыте также были бы случайными. И это как раз исключает связь функции Луи де Бройля со случайными процессами, По сути Луи де Бройль утвердил представление объектов Мироздания в одной противоположности в виде волновых процессов, а в другой противоположности в виде корпускул с массой покоя. Отсюда следует, что способ отражения корпускулярно-волновых свойств, исходя из функции Луи де Бройля (31), с соответствующим представлением значения Ψ0 по геометрии Минковского [3, с. 226] через экспоненциальную функцию с учётом нижней формулы в (1), может быть представлен в виде:
| (32) |
Это означает, что объект отображается в одной противоположности пространственно-временным искривлением, а в другой противоположности ‒ волновым процессом соответствующей частоты. При таком представлении объект имеет корпускулярно-волновое отображение в обеих противоположностях и за счёт мнимой единицы происходит смена корпускулярного представления на волновое представление, и наоборот. Учитывая необходимость однозначной связи волновых и корпускулярных свойств в каждом объекте Мироздания, с учётом обмена с условием закона сохранения количества, Дирак интуитивно предложил переход от корпускулярных свойств к волновым свойствам через уравнение энергии Эйнштейна на основе волновых функций Луи де Бройля, которые в (1) формируют общее уравнение Мироздания.
В этом случае первоначальное уравнение энергии Эйнштейна с учётом «линеаризации» имеет вид [12, с. 295-298]:
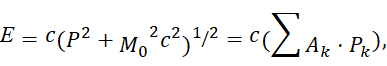 | (33) |
Здесь k изменяется от 0 до 3; P0=M0c; P1=Px ; P2=Py ; P3=Pz. Из этой записи при использовании матриц для разложения (33):
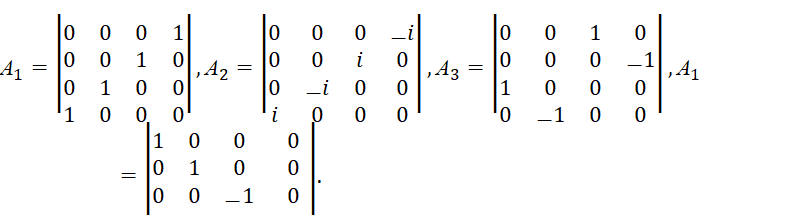 | (34) |
Следуют известные уравнения, которые дают систему уравнений Дирака. При этом система уравнений имеет вид:
| (35) |
Далее конкретные числовые значения заменяются дифференциальными операторами в виде:
| (36) |
Которые должны воздействовать на волновую функцию Ψ, и которая, в свою очередь, характеризует вероятность. В дифференциальном виде мы получим систему уравнений Дирака:
| (37) |
Понятно, что при «линеаризации» Дирак не опирался на реальные физические процессы для получения уравнения энергии Эйнштейна вида (33) и использовал функции, которые характеризуют вероятность вида:
![]() , (38)
, (38)
Такой вид соответствует функции Луи де Бройля для объектов Мироздания в отдельном замкнутом виде. Так как постоянная Планка ![]() присутствует при дифференцировании во всех членах, то её можно исключить из дальнейшего рассмотрения. Соответственно имеем вид функций при движении частицы без наличия внешних сил:
присутствует при дифференцировании во всех членах, то её можно исключить из дальнейшего рассмотрения. Соответственно имеем вид функций при движении частицы без наличия внешних сил:
![]() , (39)
, (39)
При выражении одних функций через другие, с учётом дифференцирования для свободной частицы без внешнего электромагнитного поля, получаем:
| (40) |
Далее выражаем одни функции через другие:
| (41) |
На следующем этапе подставляем одни функции вместо других и сокращаем подобные члены:
| (42) |
Сокращая на волновую вероятностную функцию Ψ1, получаем уравнение энергии Эйнштейна для взаимодействующих противоположных частиц:
| (43) |
Аналогичный результат мы имеем и для других волновых функций.
Однако следует отметить, что полученный вид через систему уравнений Дирака для движущихся корпускулярных частиц не соответствует уравнению Гамильтона ‒ Якоби, которое следует из второго закона Ньютона:
F=ma=md2s/dt2= mdv/dt; E=∫Fds=∫Fvdt=∫mvdv=mv2/2=p2/(2m). | (44) |
На следующем этапе по классической физике берётся некая функция действия S(r,t) с учётом равенств ![]() и
и ![]() . В результате имеем уравнение Гамильтона – Якоби без внешнего поля:
. В результате имеем уравнение Гамильтона – Якоби без внешнего поля:
![]() , (45)
, (45)
И в том и другом случае мы имеем движущуюся частицу без воздействия внешних сил, но законы разные, и это означает неоднозначность и парадокс. Поэтому надо показать причину такого различия и с этой целью учтём, что уравнение Гамильтона ‒ Якоби при наличии внешнего поля приобретает вид:
![]() , (46)
, (46)
Далее покажем связь данного уравнения с уравнением гармонического осциллятора, но при этом считаем, что сила притяжения потенциального поля равна силе отталкивания. При этом напомним, что гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы F=‒kx [13, с. 90]. Потенциальная энергия такой частицы имеет вид:
![]() , (47)
, (47)
Собственная частота классического гармонического осциллятора при массе частицы m0 равна:
![]() , (48)
, (48)
Далее получим формулу для потенциальной энергии частицы в виде:
![]() , (49)
, (49)
После взятия производных в (45) мы имеем уравнение:
![]() , (50)
, (50)
Понятно, что движение с ускорением связано с излучением, одновременно для получения стабильного объекта необходимо и поглощение, что было замечено Эйнштейном для описания фотоэффекта в его уравнении вида [14, с. 36]:
![]() , (51)
, (51)
Отсюда с учётом равенства поглощения и излучения для наличия соблюдения закона сохранения количества между противоположностями при Е=hf получаем формулу гармонического осциллятора в виде (23). Однако далее, исходя из получения зависимости ![]() в (24) необходимо обосновать замену потенциальной энергии
в (24) необходимо обосновать замену потенциальной энергии ![]() на кинетическую энергию
на кинетическую энергию ![]() , и наоборот. Собственно такую замену мы обосновали в [9, 5-44; 15, с. 32-56], здесь мы только укажем, какие противоречия помешали учёным прийти к необходимому результату и как они должны были быть решены с учётом правил, применённых самими физиками. Для этого более детально рассмотрим используемое в квантовой механике уравнение Шредингера, которое фактически связывает корпускулярные свойства с волновыми свойствами с учётом закона сохранения количества. При этом мы учитываем, что уравнение Шредингера без учёта внешних сил будет иметь вид [16, с. 30-31]:
, и наоборот. Собственно такую замену мы обосновали в [9, 5-44; 15, с. 32-56], здесь мы только укажем, какие противоречия помешали учёным прийти к необходимому результату и как они должны были быть решены с учётом правил, применённых самими физиками. Для этого более детально рассмотрим используемое в квантовой механике уравнение Шредингера, которое фактически связывает корпускулярные свойства с волновыми свойствами с учётом закона сохранения количества. При этом мы учитываем, что уравнение Шредингера без учёта внешних сил будет иметь вид [16, с. 30-31]:
![]() , (52)
, (52)
Собственно Шредингер попытался объединить чисто корпускулярное уравнение Гамильтона ‒ Якоби на основе второго закона Ньютона с присутствием волновых свойств. В этом случае должно быть равенство корпускулярных и волновых свойств для одного и того же уравнения, что было выполнено для случая в системе уравнений Дирака. При этом волновые функции по синусу и косинусу при подстановке в уравнение Гамильтона ‒ Якоби при взятии первой и второй производных не обеспечивают равенство. Поэтому Шредингер был вынужден использовать комплексную волновую функцию Луи де Бройля по формуле (38) с нормировкой на постоянную Планка и умножением первой производной от функции по времени на мнимую единицу. Соответственно, возведение в квадрат первой производной от функции по длине он заменил интуитивно двойным дифференцированием этой функции. В итоге волновой вид комплексной функции позволил получить решение аналогичное тому, какое следовало для уравнения Гамильтона ‒ Якоби от второго закона Ньютона. Совпадение решения для волновой функции с решением для функции для корпускулярной частицы означает возможность сочетания корпускулярных и волновых свойств в одном общем объекте. Но вид уравнений при этом оказался отличающимся. Тогда физики посчитали, что данное уравнение Шредингера должно удовлетворять условию, при котором оно должно в предельном случае переходить в уравнение Гамильтона – Якоби. С этой целью вместо волновой функции ![]() вводят функцию S при помощи соотношения [16, с. 30-31]:
вводят функцию S при помощи соотношения [16, с. 30-31]:
![]() , (53)
, (53)
Далее учитывают равенства:
| (54) |
Так как волновая функция Ψ входит во все члены лишь множителем, то её можно сократить, тогда получим:
![]() , (55)
, (55)
В предельном случае физики полагают, что при величине ![]() , мнимая составляющая пропадает и данное уравнение переходит в уравнение Гамильтона ‒ Якоби. Однако надо напомнить, что
, мнимая составляющая пропадает и данное уравнение переходит в уравнение Гамильтона ‒ Якоби. Однако надо напомнить, что ![]() , а это означает, что перехода к уравнению Гамильтона ‒ Якоби просто быть не может, так как нет варианта, при котором
, а это означает, что перехода к уравнению Гамильтона ‒ Якоби просто быть не может, так как нет варианта, при котором ![]() . А с учётом обратно-пропорциональной связи со скоростью света законов физики как таковых просто быть не может. То есть, при
. А с учётом обратно-пропорциональной связи со скоростью света законов физики как таковых просто быть не может. То есть, при ![]() , получается однородность, нарушаются законы физики и, соответственно нет и самих противоположностей. Кроме того, в дальнейшем это уравнение (55) с учётом внешнего потенциального поля используется при методе Вентцеля –Крамерса ‒ Бриллоэна (метод ВКБ) [17, с. 60] для сшивания функций на границе раздела с получением в конечном итоге правила квантования Бора ‒ Зоммерфельда, на основании чего оправдывался туннельный эффект с прохождением через потенциальный энергетический барьер, а также наличие нулевой энергии по соотношению неопределённостей Гейзенберга. При этом исчезновение члена с величиной постоянной Планка исключало доказательство всех остальных преобразований. Парадоксы таких решений мы также подробно рассмотрели в [18, с. 5-27].
, получается однородность, нарушаются законы физики и, соответственно нет и самих противоположностей. Кроме того, в дальнейшем это уравнение (55) с учётом внешнего потенциального поля используется при методе Вентцеля –Крамерса ‒ Бриллоэна (метод ВКБ) [17, с. 60] для сшивания функций на границе раздела с получением в конечном итоге правила квантования Бора ‒ Зоммерфельда, на основании чего оправдывался туннельный эффект с прохождением через потенциальный энергетический барьер, а также наличие нулевой энергии по соотношению неопределённостей Гейзенберга. При этом исчезновение члена с величиной постоянной Планка исключало доказательство всех остальных преобразований. Парадоксы таких решений мы также подробно рассмотрели в [18, с. 5-27].
Надо отметить, что Шредингер был близок к истине, если бы учёл, что основой уравнения Гамильтона ‒ Якоби для совмещения корпускулярных и волновых свойств является закон действия и противодействия для противоположностей. В этом случае должно соблюдаться равенство:
![]() , (56)
, (56)
Соответственно это равенство определяет и вид волновой функции Луи де Бройля вида ![]() :
:
![]() , (57)
, (57)
Далее мы учитываем, что Дирак любое дифференцирование ещё до нас связал с дополнительным умножением на мнимую единицу по формулам в (36). Мы лишь в теории мироздания [1, с. 5-37] дали этому логическое обоснование. Отсюда получается решение:
| (58) |
Надо отметить, что в [15, с. 32-56] мы дали логическое объяснение коэффициенту 1/(2h) в (57) как величине связи между механическим движением и магнитным моментом (это и отражает необходимость корпускулярно-волнового дуализма любого объекта), и значение ½ связано с тем, что учитывается только одна – магнитная составляющая при связи противоположностей через скорость света. Следует отметить, что величина 1/(2m0) гиромагнитного отношения по нашей теории играет основную роль в вычислении аномальных магнитных моментов. Действительно, равенство, использованное Бором в формуле (25), соответствует третьему закону Ньютона, когда сила действия при изменениях равна силе противодействия Fд=-Fпр [19, с. 56] (по сути, формула (56)). Соответственно, с учётом нашей теории по получению нижней формулы в (26), а также в соответствии с теорией Дирака, уравнение (25) примет вид:
| (59) |
При этом мы учитываем, что последнее уравнение в (59) относится к связи противоположностей как аргумента и функции, где представление через значения s соответствуют аргументу волновой функции Луи де Бройля при описании корпускулярного движения частицы. Это означает, что мы будем иметь решение для корпускулярного движения частицы по уравнению Гамильтона ‒ Якоби, если не в нашей системе наблюдения присутствует закон сохранения количества по замкнутому циклу с действием и противодействием. Причём в одной противоположности длина выражается величиной s, а в другой противоположности мы имеем эквивалент в виде (s)1/2. Так как разность в противоположности меняется на сумму, то противодействие в одной противоположности означает наличие общего объекта, выраженного через воздействие (силу) в другой противоположности. Соответственно мы учитываем, что пространственно-временное искривление, что характеризуется значением s вызвано движением в противоположности по ОТО Эйнштейна, и определяется при связи волновых и корпускулярных свойств гиромагнитным отношением 1/(2m0)=с/2. Отсюда с учётом СТО и ОТО Эйнштейна получаем выражение для коэффициента аномального магнитного момента на основе пространственного искривления которое формируется в противоположностях в виде противодействующих друг другу электрических и магнитных сил в одной противоположности и одной общей суммарной (магнитной) силы в другой противоположности (иначе отличий нет):
| (60) |
Сумма s+(s)1/2=1,7966 даёт необходимый коэффициент при вычислении аномального магнитного момента для протона [20, с. 317-318], который при практическом вычислении с учётом влияния внешней среды составил величину 1,79. Так как пространственно-временное искривление для массы протона формируется в противоположности, и именно на этом основании получается аномальный магнитный момент, то соответственно в нашей системе наблюдения этот аномальный магнитный момент, полученный на основе замкнутого действия и противодействия, не зависит от скорости движения протона как, например, дираковский магнитный момент. Далее учтём, что разница теоретического значения с экспериментом на 0,0066 связана с тем, что в (60) учитывается наличие отдельного существования одного атома водорода, а в реальности в эксперименте этого не получить. Для учёта аномального магнитного момента нейтрона необходимо учесть, что нейтральность обеспечивается наличием двух противоположных частиц, и коэффициент для аномального магнитного момента нейтрона формируется суммой и разностью, и разностью от них в силу взаимодействия. Так как сложение в одной противоположности означает вычитание в другой противоположности, то результат такого замкнутого взаимодействия [‒s‒(s)1/2‒(s)1/2+s]=2(s)1/2=‒1,86. Собственно такое предположение связано с процессом реальных изменений с превращением протона в нейтрон и нейтрона в протон по реакциям синтеза и распада. Примером электронного захвата может служить превращение калия К40 в аргон Ar40 [21, с. 248]:
![]() , (61)
, (61)
Обратный процесс можно привести на примере превращение азота N13 в углерод С13:
![]() , (62)
, (62)
Понятно, что взаимодействие частиц с их превращением в новые частицы осуществляется через окружающую среду, а значит, зависит от её пространственно-временного искривления. Это в корне отличается от концепции физиков, которые пытаются получить нейтрон за счёт кинетической энергии и столкновения протонов в результате преодоления неких ядерных сил. Иными словами, мы видим, что аномальные магнитные моменты связаны с физикой реального процесса пространственно-временного искривления за счёт замкнутого движения в противоположностях. Кроме того, не надо думать, что указанные вычисления для аномального магнитного момента через движение с учётом разного представления объектов в противоположных системах наблюдения ‒ это наши выдумки. Как не хотели физики, но они были вынуждены при описании аномального магнитного момента использовать орбитальное движение виртуальных пи-мезонов [22, с. 240], что, собственно, также определяется связью магнитных свойств с движением через гиромагнитное отношение. Кроме того, они использовали для описания аномальных магнитных моментов мифические кварки и создали противоречие с неоднозначной связью электрических и магнитных сил из-за дробности зарядов при одном и том же магнитном спине. Мы же, исходя из СТО и ОТО Эйнштейна, также ориентируемся на орбитальное движение, но в противоположностях на другом уровне иерархии в соответствующих системах наблюдения. Само изменение представления о взаимодействиях в противоположностях, при переходе от одной системы наблюдения в другую систему, связано с исключением однородности, с учётом изменения разности на сумму (иначе нет различий между противоположностями). Однако использование кварков дало ещё один парадокс, при котором значение магнитного момента кварка невозможно вычислить, так как неизвестно само его происхождение. Поэтому физиками делается очередная подгонка под результат, при которой значение магнитного момента кварка выбирается равной общему значению магнитного момента протона, с учётом, как аномального магнитного момента, так и обычного магнитного момента ![]() , то есть
, то есть ![]() . В итоге для аномального магнитного момента нейтрона физики получили [23, с. 297]:
. В итоге для аномального магнитного момента нейтрона физики получили [23, с. 297]:
![]() , (63)
, (63)
Собственно полученный коэффициент в (63) совпадает с нашими вычислениями, но при эксперименте получена величина ‒1,91. С точки зрения нашей теории это связано с тем, что условия эксперимента не могут быть идентичными условиям теоретического расчёта из-за влияния окружающей среды. Таким образом, выбор у оппонентов небольшой, либо ориентироваться на чудеса орбитального движения в виде виртуальных частиц (какие при этом размеры орбитали или орбиты тоже не известны), возникающих и исчезающих в ноль, либо рассматривать взаимодействие за счёт движения в зависимости от системы наблюдения, что следует из СТО и ОТО Эйнштейна и нами подробно рассмотрено в [15, с. 32-56].
Однако, теперь попытаемся понять, есть ли возможность перехода от уравнения (56) с волновой функцией Ψ по (57) к корпускулярному движению частицы, как это получилось для системы уравнений Дирака [12, с. 295-298]. Иными словами, мы пытаемся доказать, что уравнение Гамильтона ‒ Якоби не полностью описывает частицу исходя из корпускулярно-волнового дуализма, то есть замкнутой системы. Следовательно, теперь надо разобраться, что, собственно, даёт учёт взаимодействия корпускулярных и волновых свойств, при законе сохранения количества за счёт перехода от возведения в квадрат первой производной функции от длины в уравнении Гамильтона ‒ Якоби к двойному дифференцированию по длине этой же функции. Если волновая функция Ψ имеет вид (57), то мы имеем уравнение Гамильтона ‒ Якоби (58). Однако, если исходить из (53), то здесь учитывается и изменение самого аргумента. То есть уравнение Шредингера может рассматривать процесс во взаимосвязи противоположностей, а не в варианте наличия одной противоположности по волновой функции Ψ с видом (57). При этом должно соблюдаться условие закона сохранения количества, так как объект не исчезает в результате движения.
В нашем случае, функция S(r,t) отражает изменяемую величину всего аргумента как единого целого, и поэтому мы будем иметь вид без нормировочного коэффициента в виде величины постоянной Планка:
![]() , (64)
, (64)
В итоге с учётом правила дифференцирования с умножением на мнимую единицу, предложенного в (36) Дираком, и доказанного в нашей теории [1], получаем равенства:
| (65) |
С учётом (64) и поскольку волновая функция Ψ в результате данного преобразования должна входить во все члены лишь множителем, мы можем её сократить. В итоге получаем:
![]() , (66)
, (66)
При учёте волновой функции Ψ вида (64) в одной системе наблюдения и волновой функции от аргумента ![]() в противоположной системе наблюдения, с учётом того, что дифференцирование соответствует условиям Дирака вида (36), мы имеем уравнение:
в противоположной системе наблюдения, с учётом того, что дифференцирование соответствует условиям Дирака вида (36), мы имеем уравнение:
| (67) |
Иными словами, мы показали переход от гармонического осциллятора (23) к верхнему уравнению в (24) на основе полного уравнения Гамильтона ‒ Якоби с учётом сил в виде потенциальной энергии (которое и определяет уравнение гармонического осциллятора), и с изменением аргумента S при функции Ψ. То есть при учёте корпускулярно-волнового дуализма движущегося объекта полное уравнение Гамильтона – Якоби соответствует уравнению гармонического осциллятора, которое также соответствует уравнению окружности. А выше мы также показали, как уравнение окружности переходит в уравнение энергии Эйнштейна, из которого выводится система уравнений Дирака. Тем самым мы разрешили парадокс неоднозначности, который был между уравнением энергии Эйнштейна и уравнением Гамильтона – Якоби исходя из наличия корпускулярно-волнового дуализма. Соответственно, если уравнение Гамильтона ‒ Якоби (46) описывает корпускулярное движение частицы в некотором внешнем потенциальном поле, то уравнение (66) описывает условие сохранения самой частицы как корпускулярно-волнового объекта на основе равенства силы действия и противодействия с учётом кинетической и потенциальной энергии. Таким образом, интуитивные подходы физиков, которые использовались при практических расчётах, имеют логическое обоснование по нашей теории с учётом наших поправок на основе того, что уже было предложено самими физиками, но требовало разъяснений.
Однако мы должны отметить, что использованные Шредингером и Дираком волновые функции Луи де Бройля описывались как волновые функции, характеризующие вероятность, и никак не были связаны с реально существующими электромагнитными функциями. Но, так как мы не можем опираться на чудеса вероятностей в замкнутой системе Мироздания, то возникает вопрос: «Как совместить волновые функции Луи де Бройля, которые соответствуют функциям в уравнении (1) с электромагнитными функциями?» Понятно, что в этом случае система уравнений Дирака должна вытекать из законов электродинамики, которые в свою очередь должны следовать из общей формулы Мироздания (1). Подробно описание такого перехода мы показали в [24, с. 5-36]. Сейчас мы уделим особое внимание симметрии преобразований противоположностей при переходе от корпускулярного вида к волновому виду, и наоборот. С этой целью мы попытаемся объяснить необходимость первоначальной формулы, используемой в электродинамике по связи магнитных и электрических полей вида [25, с. 25]:
| (68) |
Здесь ![]() и
и ![]() константы магнитной и электрической проницаемости окружающей среды. В классической электродинамике в системе измерения СИ используется формула для вычисления волнового сопротивления среды в виде [26, с. 299]:
константы магнитной и электрической проницаемости окружающей среды. В классической электродинамике в системе измерения СИ используется формула для вычисления волнового сопротивления среды в виде [26, с. 299]:
![]() , (69)
, (69)
Для системы измерения СГС вообще нет констант электрической и магнитной проницаемости в окружающей среде (вакууме) и таким образом вакуум соответствует геометрии Эвклида. В системе СИ электрическая и магнитная составляющая волны в среде распространения отличаются друг от друга только количественно, и не являются противоположностями, как, например, длина и время, которые связаны по теории Минковского [3, с. 226] через скорость света. А если отличия только количественные, то это означает, что и законы физики должны быть одинаковые, чего на практике не наблюдается, так как нет никаких магнитных зарядов в пространстве, которые физики безуспешно ищут. Кроме того, отсутствие отличий исключает и взаимодействие, что соответствует противоположностям, так как для величин отличающихся только количественно происходит ассоциативное сложение или вычитание. Это означает парадокс и отсюда следует, что должна быть иная интерпретация констант электрической и магнитной проницаемости, при которой мы имели представление электрических и магнитных составляющих как противоположностей. Учитывая скорость распространения электромагнитных волн со скоростью света, нам остаётся предположить, что электромагнитные составляющие относятся к противоположной системе наблюдения, где выполнение по преобразованиям Лоренца ‒ Минковского соблюдается на основе проекции скорости на время. В этом случае кинетическая энергия электромагнитной волны в противоположной системе наблюдения будет выражаться потенциальной энергией по ОТО Эйнштейна в нашей системе наблюдения через константы электрической и магнитной проницаемости.
Поэтому, нам следует выразить константы магнитной и электрической проницаемости через усреднённое (интегральное) движение частиц, со скоростью (кинетической энергией) в противоположной системе наблюдения ![]() , связанной с нашей системой наблюдения через скорость света. Усреднённое интегральное значение кинетической энергии от противоположности говорит о том, что любая частица в одной противоположности связана с взаимодействием и всеми частицами в другой противоположности. И это тоже не наша выдумка, так как на этом построена идея получения формулы Планка для замкнутой системы с исключением варианта «ультрафиолетовой катастрофы», с использованием закона Больцмана вида
, связанной с нашей системой наблюдения через скорость света. Усреднённое интегральное значение кинетической энергии от противоположности говорит о том, что любая частица в одной противоположности связана с взаимодействием и всеми частицами в другой противоположности. И это тоже не наша выдумка, так как на этом построена идея получения формулы Планка для замкнутой системы с исключением варианта «ультрафиолетовой катастрофы», с использованием закона Больцмана вида ![]() . По сути, это закон связи между распадом в одной противоположности и синтезом в другой противоположности. Отсюда имеем формулы для констант магнитной и электрической проницаемости в виде:
. По сути, это закон связи между распадом в одной противоположности и синтезом в другой противоположности. Отсюда имеем формулы для констант магнитной и электрической проницаемости в виде:
| (70) |
В этом случае константы электрической и магнитной проницаемости не имеют аналогичный вид, а это даёт их представление как противоположностей, и поэтому они отличаются на значение с2. Понятно, что наличие констант электрической и магнитной проницаемости в окружающей среде должно определять и соответствующие параметры частиц в Мироздании, так как взаимодействие частиц происходит именно через параметры окружающей среды. Поэтому с учётом нашей теории масса протона вычисляется исходя из волнового сопротивления среды распространения с учётом максимума энергии излучения по формуле Планка с учётом коэффициента 4,965 [27, с. 27]. Здесь мы учитываем, что в отличие от системы СИ у нас отношение ![]() , а не просто число
, а не просто число ![]() [26, с. 299]. В итоге получаем уравнение для отношения массы протона к массе электрона:
[26, с. 299]. В итоге получаем уравнение для отношения массы протона к массе электрона:
![]() , (71)
, (71)
Некоторое небольшое отличие от практики (1836,1) в числовом значении есть, и оно связано с тем, что наши расчёты выполнены для более общего случая с делением только на протон и электрон. Кроме того, при динамике обмена обязательно должна быть энергия с соответствующей массой для излучения. Таким образом наша теория позволяет определить и разницу масс между протоном и электроном на основе СТО и ОТО Эйнштейна. Понятно, что в силу симметрии между противоположностями и замкнутости Мироздания, начальные значения напряжённостей электрических и магнитных полей так же, как и начальные значения длины и времени по геометрии Минковского [3, с. 226] должны быть связаны через скорость света, то есть Н=сЕ. Собственно, только в этом случае можно объяснить отсутствие магнитных зарядов в нашей системе наблюдения и отличие законов для силы Кулона и Лоренца.
| (72) |
Иными словами, мы имеем инвариантную форму в нашей системе наблюдения вне зависимости от движения в противоположности согласно ОТО Эйнштейна при представлении через одну общую переменную Е, аналогично пространственно-временному искривлению согласно (15) в соответствии с СТО в нашей системе наблюдения. При Е=с имеем Е2=с2=с/h=Nоб=const. Это фактически соблюдение закона сохранения количества объектов при преобразованиях. Кроме того, окружающая среда (вакуум) не может описываться через Эвклидову геометрию, с отсутствием констант электрической и магнитной проницаемости. То есть, любой объект мироздания является корпускулярно-волновым объектом с описанием, как через электромагнитные составляющие, так и через пространство и время, и в этом случае мы имеем общий пространственно-временной и электромагнитный континуум с взаимным переходом составляющих друг в друга, что определяется замкнутостью Мироздания. Собственно этот взаимный переход и составляет интерес наших дальнейших исследований с целью выявления, каким образом электромагнитные составляющие при взаимодействии дают корпускулярное движение частиц, и наоборот. Понятно, чтобы получить взаимосвязь корпускулярных и волновых свойств надо иметь представление уравнений электродинамики аналогичное представлению уравнений в системе Дирака. И надо отметить, что некоторое подобие физики получили в классической электродинамике. То есть физики вывели волновые равенства в комплексном виде на основе векторных потенциалов и с взятием производной по времени в [28, с. 39-40]:
| (73) |
Уравнения в (73) фактически отражают получение волновых процессов на основе источников излучения, которые формируются за счёт изменения (преобразования) сторонних электрических и магнитных токов. Понятно, что преобразование нечто нереального невозможно и отсюда уже должен был следовать вывод, что если данные токи не наблюдаются в нашей системе наблюдения, то должна быть противоположная иная система наблюдения, где эти сторонние токи должны иметь реальное воплощение через движение реальных частиц. Иначе чуда не избежать. Собственно такой вывод уже следовал из СТО и ОТО Эйнштейна, где время не наблюдаемая в пространстве величина превращалась в эквивалент длины в зависимости от скорости, и наоборот. Однако представленный вид уравнений в (73) не соответствует полностью виду (37), который используется для получения корпускулярного движения частицы, поэтому детально этот переход мы показали в [24, с. 5-36]. Здесь мы остановимся лишь на последовательности логики получения указанного перехода с учётом симметрии законов в противоположностях. В соответствии с этим нами были использованы усовершенствованные уравнения Максвелла вида:
| (74) |
Однако векторное представление не показывает полную схему преобразования по координатам. Поэтому при росписи по отдельным координатам для усовершенствованных уравнений Максвелла мы получим вид:
| (75) |
Исходя из преобразований противоположностей друг в друга через комплексные функции, существует и комплексно-сопряжённой форма записи, в зависимости от знака у мнимой единицы (![]() ). В итоге система уравнений (74) дала при подстановке одних уравнений в другие, что отражает взаимодействие, волновые процессы вида:
). В итоге система уравнений (74) дала при подстановке одних уравнений в другие, что отражает взаимодействие, волновые процессы вида:
| (76) |
Однако в (73) по первым двум уравнениям ![]() мы имеем источники возбуждения, что соответствует принципу Гюйгенса ‒ Френеля. Причём эти источники возбуждения
мы имеем источники возбуждения, что соответствует принципу Гюйгенса ‒ Френеля. Причём эти источники возбуждения ![]() должны иметь отображение в напряжённостях электрических и магнитных полей с учётом параметров окружающей среды, так как иначе отсутствует взаимодействие с возможностью смены направления движения, что на практике не наблюдается. Однако в классической электродинамике [28, с. 39-40] источники возбуждения на основе Е и Н выражаются через векторные потенциалы, а не через сторонние электрические и магнитные токи в виде:
должны иметь отображение в напряжённостях электрических и магнитных полей с учётом параметров окружающей среды, так как иначе отсутствует взаимодействие с возможностью смены направления движения, что на практике не наблюдается. Однако в классической электродинамике [28, с. 39-40] источники возбуждения на основе Е и Н выражаются через векторные потенциалы, а не через сторонние электрические и магнитные токи в виде:
| (77) |
Соответственно необходимо показать, каким образом решается указанная неоднозначность по нашей теории. С этой целью нам необходимо показать, чем являются векторные потенциалы и сторонние токи по отношению друг к другу. Собственно, и здесь мы не являемся первопроходцами, и эта связь была получена в классической электродинамике в виде уравнения Даламбера, например, на основе электрического стороннего тока с наличием волнового представления векторных потенциалов в виде [29, с. 119]:
| (78) |
Это означает, что волновой электромагнитный процесс, отражённый через векторный потенциал в противоположной системе наблюдения определяется процессом пространственно-временного искривления среды распространения уже в нашей системе наблюдения на основе стороннего электрического тока. Это говорит о том, что формирование так называемого фонового излучения по формуле Планка связано с пространственно-временным искривлением окружающей среды на основе констант электрической и магнитной проницаемости, и это противоречит концепции физиков о возникновении и исчезновении виртуальных фотонов в электромагнитном вакууме. Само же пространственно-временное искривление в нашей системе наблюдения связано с корпускулярным движением частиц в противоположной системе наблюдения, и наоборот. Здесь также используется калибровка Лоренца вида ![]() . При этом мы имеем
. При этом мы имеем ![]() . Это означает, что смена системы наблюдения, о чём говорит смена переменных дифференцирования, приводит к тому, что компенсация в одной системе наблюдения означает сумму в другой системе наблюдения. То есть физики уже до нас утвердили правило смены суммы на разность в зависимости от системы наблюдения от противоположностей. При связи сА=Ф, аналогично первоначальной связи по длине и времени (r=ct, по идее Минковского [3, с. 226]) и переходе к единому отображению переменных в одинаковых величинах имеем
. Это означает, что смена системы наблюдения, о чём говорит смена переменных дифференцирования, приводит к тому, что компенсация в одной системе наблюдения означает сумму в другой системе наблюдения. То есть физики уже до нас утвердили правило смены суммы на разность в зависимости от системы наблюдения от противоположностей. При связи сА=Ф, аналогично первоначальной связи по длине и времени (r=ct, по идее Минковского [3, с. 226]) и переходе к единому отображению переменных в одинаковых величинах имеем ![]() и
и ![]() . Таким образом, то, что является разностью от системы наблюдения от А, является суммой от системы наблюдения от Ф, которые как противоположности связаны через скорость света.
. Таким образом, то, что является разностью от системы наблюдения от А, является суммой от системы наблюдения от Ф, которые как противоположности связаны через скорость света.
Теперь надо показать, что уравнения для векторных потенциалов идентичны усовершенствованным уравнениям Максвелла, что характеризует векторные потенциалы как величины, отражающие электромагнитные свойства в противоположности. Это можно сделать с учётом равенств электрических и магнитных полей по уравнениям через векторные потенциалы в виде:
| (79) |
Физики при использовании систем измерения СИ или СГС не могли прийти к наличию такого равенства. Соответственно изменения векторных потенциалов связаны с движением корпускулярных частиц в противоположной системе наблюдения. Именно это и было применено Фейнманом [30, с. 265], но с ошибкой описания векторных потенциалов в той же системе наблюдения, что и электромагнитные составляющие с выводом наличия полей от значения, движущегося и неподвижного заряда, что также применяется и для электромагнитных составляющих. Это означает двойственность образования электромагнитных полей. С одной стороны, зависимость электромагнитных составляющих от заряда, за счёт значений по длине и времени, прямая, а для векторных потенциалов электромагнитные поля зависят от того же заряда, но с взятием производных от длины и времени. В итоге получается парадокс, при котором электрическое поле при изменении формирует само себя, что было показано нами в [9, с. 5-44]. Отсюда, суть разницы с нашей теорией в том, что в нашем случае результат образования электромагнитных составляющих в нашей системе наблюдения (а это, по сути, источники возбуждения электромагнитных полей) связан с обменным процессом от производных векторных потенциалов в противоположной системе наблюдения. Это достигается за счёт замкнутого движения частиц в виде ротора (по сути, это гармонический осциллятор), и прямолинейном движении частиц (если считать тангенциальную составляющую скорости), где обменный замкнутый процесс связан с преобразованием длины в проекцию на время в соответствии с СТО Эйнштейна, и наоборот. При этом наш подход позволил доказать симметрию представления электромагнитных процессов в противоположных системах наблюдения, при которых усовершенствованные уравнения Максвелла (75) имеют аналогичный вид представления через векторные потенциалы:
| (80) |
Здесь i=(‒1)1/2, которая также впервые была введена не нами в уравнения Максвелла и использовалась для комплексных значений электрической и магнитной проницаемости, что мы показали в [24, с. 5-36].
Напомним, что сам принцип наличия противоположной системы наблюдения с преобразованием корпускулярных свойств в волновые свойства, и наоборот, был придуман не нами, а следовал из СТО и ОТО Эйнштейна, в силу того, что Эйнштейн в ОТО фактически ввёл для описания пространственно-временного искривления, для отражения значений скоростей, абсолютную систему отсчёта, связанную с нашей через скорость света. Понятно, что скорость, отражающая пространственно-временное искривление по ОТО Эйнштейна, не может представляться через значения по координатам осей в трёхмерном пространстве. Для такой скорости с учётом абсолютной системы отсчёта, связанной с нашей системой наблюдения через скорость света, отображение связано с проекцией на время. Соответствие напряжённостей электромагнитных полей для подчинения СТО и ОТО Эйнштейна физики попытались связать по формуле, которая аналогична формуле связи длины и времени в виде:
| (81) |
В итоге Фейнман получил выражение [31, с. 269]:
![]() , (82)
, (82)
Сравнивая нижнее уравнение (81) с уравнением (82), мы видим отличие (82) от нижнего уравнения (81) в том, что в уравнение (82) входит константа магнитной проницаемости ![]() , которая характеризует состояние среды распространения. Соответственно есть разница и на величину
, которая характеризует состояние среды распространения. Соответственно есть разница и на величину ![]() . Отсюда можно сделать следующие преобразования формулы (82):
. Отсюда можно сделать следующие преобразования формулы (82):
| (83) |
Последнее уравнение в (83) соответствует замкнутой системе двух противоположностей по уравнению окружности с учётом обратно-пропорциональной связи. Это совпадает с результатом в (30), которое получено из формулы Луи де Бройля hf=mc2. Иными словами, мы получаем один и тот же закон, что означает симметрию в противоположностях, и соответствует представлению электромагнитных составляющих в одной системе наблюдения как величин длины (массы) и времени (обратно-пропорциональна частоте) в противоположной системе наблюдения.
При этом в усовершенствованных уравнениях Максвелла присутствует и магнитный сторонний ток. Это также было замечено физиками в [32, с. 36] и магнитный сторонний ток впервые ввели не мы. Отсюда был определён векторный потенциал для напряжённости электрического поля вида:
![]() , (84)
, (84)
Одновременно для напряжённости магнитного поля по аналогии должен быть вид:
![]() , (85)
, (85)
Далее, исходя из уравнения вида ![]() , имеем:
, имеем:
| (86) |
В результате мы имеем зависимость между сторонними (фиктивными) электрическими и магнитными токами вида:
| (87) |
Это означает, что мы имеем обратно-пропорциональную зависимость между сторонними электрическими и магнитными токами, которая совпадает с обратно-пропорциональной зависимостью для объектов длины и времени по СТО Эйнштейна с соблюдением инвариантности. По сути дела, исходя из значений констант электрической и магнитной проницаемости мы получаем, что в уравнениях волны через векторные потенциалы А и Ам отображаются значения электрической и магнитной индукции в соответствующей системе наблюдения. При этом сторонние электрические и магнитные токи отражают иное представление, чем в системе наблюдения по уравнениям (73), и они фактически отображают значения Мэ и Мм, что означает смену системы наблюдения. Однако отметим вид уравнений (87) не может дать равенства в силу того, что слева от знака равенства присутствует волновая функция, а справа от знака равенства она отсутствует. Это несоответствие было исправлено Шредингером, который ввёл в квантовой механике умножение на волновую функцию Ψ в [16, с. 30-31] для обеих частей равенства:
![]() , (88)
, (88)
Собственно такое изменение имеет объяснение на основе нашей теории, где в уравнениях Максвелла сторонние токи имеют вид производных от волновых функций в виде (74), а само наличие представления объектов через волновые функции связано с необходимостью изменения объектов при условии их сохранения (отсюда экспоненциальный вид функций) на основе наличия корпускулярно-волнового дуализма.
В итоге с учётом смены системы наблюдения на противоположную систему, когда масса и скорость в противоположностях меняются местами (это фактически ввёл Бор с учётом обратно-пропорциональной связи и следует также из нашей теории), при ![]() имеем вид уравнений:
имеем вид уравнений:
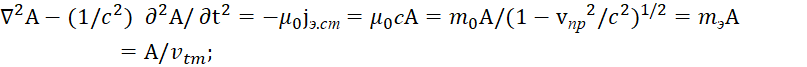 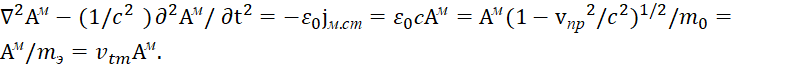 | (89) |
Таким образом, если для формирования магнитного или электрического волнового процесса в нашей системе наблюдения требовалась динамика изменения электрических и магнитных сторонних токов (76), то в противоположной системе наблюдения уже сам сторонний электрический или магнитный ток с учётом (89) выступает источником формирования волновых процессов в противоположности. Иными словами, в одной системе наблюдения сторонние токи в динамике своего изменения (преобразования) формируют источник возбуждения волновых свойств, а в другой системе наблюдения уже сами являются источниками возбуждения волновых процессов. Однако в (89) мы имеем представление векторных потенциалов через первоначальную связь противоположностей через скорость света вида: сА=Ам, при этом волновые процессы в противоположности определяются состоянием среды распространения без корпускулярного движения частиц. Поэтому, для случая реального отображения этих векторных потенциалов в пространстве и времени в нашей системе наблюдения через корпускулярное движение частиц мы должны иметь их реальное преобразование в соответствии с СТО и ОТО Эйнштейна в зависимости от скорости в нашей системе наблюдения. Иное представление только в виде электромагнитных волн исключает обмен через излучение и поглощение из-за ассоциативного сложения и вычитания. Такое преобразование по аналогии с электромагнитными составляющими в (83) было также введено физиками на основе известной формулы связи векторных потенциалов из электродинамики [33, с. 165]:
![]() , (90)
, (90)
Здесь Ф=Ам. Собственно представление в (90) соответствует описанию движения объектов в нашей системе наблюдения с выполнением СТО Эйнштейна. Отсюда при переходе в систему наблюдения от векторного потенциала Ам имеем для верхнего уравнения (89):
| (91) |
При этом для волновых свойств, при скорости движения волны со скоростью света, мы учитываем, что в соответствующей системе наблюдения Ам=сА. Данный подход соответствует идее Луи де Бройля, где волновой процесс в одной противоположности однозначно связан с импульсом движения частицы в другой противоположности с учётом обмена между противоположностями со скоростью света. Это отличается от концепции физиков, где формирование электромагнитного поля связывают с неким электрическим зарядом, который не имеет энергии, так как не входит в уравнение энергии Эйнштейна, что было учтено Дираком (![]() ). Следовательно, если в случае отображения от системы наблюдения от векторного потенциала Ам мы имели зависимость формирования волнового процесса от константы магнитной проницаемости, выраженной через неподвижное пространственно-временное искривление в виде массы
). Следовательно, если в случае отображения от системы наблюдения от векторного потенциала Ам мы имели зависимость формирования волнового процесса от константы магнитной проницаемости, выраженной через неподвижное пространственно-временное искривление в виде массы ![]() , то при отображении через векторный потенциал А, мы имеем представление от системы, связанной с наблюдением от времени, в которой масса
, то при отображении через векторный потенциал А, мы имеем представление от системы, связанной с наблюдением от времени, в которой масса ![]() уже движется со скоростью
уже движется со скоростью ![]() . Отсюда сохранение вида объектов при переходе в противоположность, например, только с заменой длины на время, и наоборот, исключало бы возможность взаимодействия и различия объектов за счёт изменения. Действительно представление изменения окружающей среды в противоположностях путём превращения длины на время, и наоборот, даёт однородность без объектов. А это означает отсутствие взаимодействия. Для нижнего уравнения в (89) мы должны учесть, что масса и скорость в противоположностях в соответствии с (26) и (89) меняются местами с учетом обратно-пропорциональной связи (r=m=1/v) и в этом случае мы имеем уравнение (90) в виде:
. Отсюда сохранение вида объектов при переходе в противоположность, например, только с заменой длины на время, и наоборот, исключало бы возможность взаимодействия и различия объектов за счёт изменения. Действительно представление изменения окружающей среды в противоположностях путём превращения длины на время, и наоборот, даёт однородность без объектов. А это означает отсутствие взаимодействия. Для нижнего уравнения в (89) мы должны учесть, что масса и скорость в противоположностях в соответствии с (26) и (89) меняются местами с учетом обратно-пропорциональной связи (r=m=1/v) и в этом случае мы имеем уравнение (90) в виде:
![]() , (92)
, (92)
Отсюда получаем:
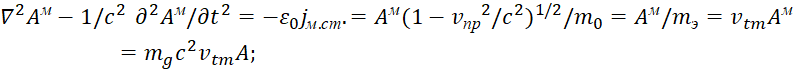 | (93) |
Таким образом, мы видим, что волновой процесс в одной системе наблюдения формируется за счёт корпускулярного движения в противоположной системе наблюдения, и наоборот. Фактически мы имеем закон, по которому движущийся электрон в одной системе наблюдения представляется протоном в другой системе наблюдения, за счёт смены скорости на массу, и данные представления частиц определяются на основе составляющих электромагнитной волны в соответствующей системе наблюдения.
Это как раз и говорит о том, что представление одного и того же объекта зависит от системы наблюдения и этот вывод, кстати, следовал по логике из уравнений, полученных самими физиками. Наша заслуга лишь в том, что мы учли, что в соответствии с СТО и ОТО Эйнштейна, с учётом связи противоположностей через скорость света, проекция на время переходит в проекцию длины, и наоборот, а это уже означает отображение в реальном виде в пространстве. Иными словами, то, что в одной системе наблюдения представляется в виде неподвижных объектов длины и времени с отображением через электрические и магнитные сторонние токи в виде пространственно-временного континуума через константы электрической и магнитной проницаемости, в противоположной системе наблюдения выглядит в качестве движущихся объектов длины и времени (противоположные заряды). Понятно, что сохранение вида объектов в обеих системах наблюдения исключает преобразование (распад или синтез объектов) с наличием самих противоположностей. Собственно, мы доказали, что формирование волновых электромагнитных полей связано как с движением корпускулярно-волновых объектов, так и при их представлении в качестве окружающей среды распространения в соответствии с гипотезой Луи де Бройля. При этом, как мы показали в [24, с. 5-36], что волновые свойства для напряжённостей электрических и магнитных полей получаются также и в результате подстановки усовершенствованных уравнений Максвелла (электронные и мюонные нейтрино и антинейтрино) друг в друга, то есть всё определяется составляющими при взаимодействии.
Необходимость формирования источников возбуждения электромагнитных полей от двух противоположностей, физиками в классической электродинамике была также предложена в виде записи через векторные потенциалы по формулам (77). Иными словами, физики фактически заменили и без нас электрические и магнитные сторонние токи в (73) и (76) на векторные потенциалы. Отличие в том, что по нашей теории без взятия производной по времени источники возбуждения представляются в виде сумм:
| (94) |
Анализируя уравнения (73), (89) и (94), мы видим, что вид волновых уравнений (89) и (94), в левой части от знака равенства совпадает при замене сторонних токов на векторные потенциалы. Отличие между сторонними токами и векторными потенциалами касается лишь знаков сложения и вычитания, что может означать смену системы наблюдения на противоположную систему. Отсюда, в соответствии с необходимостью симметрии между противоположностями для соблюдения закона сохранения количества, а также учитывая идентичность формул для векторных потенциалов и электромагнитных составляющих, что мы показали в [24, с. 5-36], можно сделать и обратную подстановку электромагнитных составляющих в векторные потенциалы. В результате по аналогии с (89) мы получим:
| (95) |
Полученные уравнения соответствуют соблюдению принципа Гюйгенса-Френеля с учётом вторичного излучения, в этом случае при ![]() мы имеем решения вида:
мы имеем решения вида:
| (96) |
Понятно, что при отсутствии вторичных источников излучения волновые уравнения оказываются полностью независимыми от среды распространения, что не наблюдается на практике. Иными словами, мы видим полное совпадение вида законов для электромагнитных составляющих и векторных потенциалов, но с отображением этих законов в противоположностях. При условии закона сохранения количества в объектах при поглощении и излучении, что связано с равенством процессов в противоположностях, выраженных через волновой электромагнитный вид, и волновой вид через векторные потенциалы, мы можем сделать замену источников возбуждения Е и Н на векторные потенциалы. То есть равный количественный обмен между противоположностями позволяет привести уравнения в зависимости от одной переменной. Для учёта волновых свойств от напряжённости электрического поля с учётом принципа Гюйгенса ‒ Френеля имеем:
| (97) |
Для учёта волновых свойств от напряжённости магнитного поля с учётом принципа Гюйгенса ‒ Френеля имеем:
| (98) |
Здесь мы учитываем, что напряжённости электрических и магнитных полей – это противоположности к векторным потенциалам, что определяется умножением на мнимую единицу, и такой переход впервые ввели не мы, а было сделано в квантовой механике в виде x4=ict или iФ=А4 [20, с. 317-318]. Кроме того, в силу противодействия электрической составляющей к магнитной составляющей, мы должны при переходе к общей системе наблюдения сделать замену знаков, так как законы физики, связанные с количественными изменениями, не могут иметь двузначный вид для одной общей переменной. Собственно, в предпоследнем уравнении в (96) смену знака перед значением ротора (![]() ) с минуса на плюс можно рассматривать как смену действия на противодействие, или как смену переменных по координатам длины, так как иное в противоположных системах наблюдения означает отсутствие преобразований с влиянием противоположностей друг на друга. Таким образом, мы получаем два уравнения относительно одной переменной
) с минуса на плюс можно рассматривать как смену действия на противодействие, или как смену переменных по координатам длины, так как иное в противоположных системах наблюдения означает отсутствие преобразований с влиянием противоположностей друг на друга. Таким образом, мы получаем два уравнения относительно одной переменной ![]() в виде:
в виде:
| (99) |
То есть так как объекты сохраняются, то вместо электрических и магнитных сторонних токов можно ввести векторные потенциалы, исходя из идентичности законов в противоположностях. Здесь учитывается, что если для формирования магнитного или электрического волнового процесса в нашей системе наблюдения требовалась динамика изменения электрических и магнитных сторонних токов (76), то в противоположной системе наблюдения уже сам сторонний электрический или магнитный ток с учётом (89) выступает источником формирования волновых процессов в противоположности. В силу симметрии законов Мироздания в противоположностях для соблюдения закона сохранения количества это правило распространяется и на векторные потенциалы, а также электромагнитные составляющие.
Таким образом, мы выразили уравнения через векторные потенциалы, с учётом, что, ![]() и
и ![]() . Иными словами, мы учитываем, что векторный потенциал по координате длины отличается от векторного потенциала по координате времени на величину, связанную с усреднённой интегральной кинетической энергией в противоположности, выраженной через значение скорости
. Иными словами, мы учитываем, что векторный потенциал по координате длины отличается от векторного потенциала по координате времени на величину, связанную с усреднённой интегральной кинетической энергией в противоположности, выраженной через значение скорости ![]() по уравнению вида:
по уравнению вида: ![]() в соответствии с ОТО Эйнштейна. Здесь аналог для магнитных составляющих
в соответствии с ОТО Эйнштейна. Здесь аналог для магнитных составляющих ![]() , и аналог для электрических составляющих
, и аналог для электрических составляющих ![]() . Если исходить из известных законов физики, то в уравнениях (98) значение
. Если исходить из известных законов физики, то в уравнениях (98) значение ![]() выражает закон Фарадея, а уравнение
выражает закон Фарадея, а уравнение ![]() соответствует поглощению или излучению в окружающей среде. Однако с точки зрения нашей теории и с целью исключения парадоксов замкнутая система ротора определяет объект в виде константы в противоположности
соответствует поглощению или излучению в окружающей среде. Однако с точки зрения нашей теории и с целью исключения парадоксов замкнутая система ротора определяет объект в виде константы в противоположности ![]() , а оставшаяся часть определяет динамику изменения между противоположностями в пространстве и времени в виде
, а оставшаяся часть определяет динамику изменения между противоположностями в пространстве и времени в виде ![]() в соответствии с СТО и ОТО Эйнштейна. Действительно, если допустить, что изменения по времени не приводят к изменениям по длине в соответствии с СТО и ОТО Эйнштейна, то тем самым исключается связь противоположностей и парадоксы с чудесами неизбежны.
в соответствии с СТО и ОТО Эйнштейна. Действительно, если допустить, что изменения по времени не приводят к изменениям по длине в соответствии с СТО и ОТО Эйнштейна, то тем самым исключается связь противоположностей и парадоксы с чудесами неизбежны.
В результате мы видим, что уравнения (98) и (99) имеют сходство с видом уравнений из системы Дирака (37), а отсюда естественно возникает мысль, что с целью исключения чудес, необходимо показать замену волновых функций, характеризующих вероятность, на реальные электромагнитные функции, которые однозначно связаны с векторными потенциалами. С этой целью вспомним, что система уравнений Дирака при массе покоя равной нулю m0=0 в квантовой механике переходит в волновые уравнения нейтрино и антинейтрино (рис. 2).
Рис. 2. Нейтрино и антинейтрино
Понятие «материи» не имеет в нашей теории никакого физического обоснования, так как не имеет математического описания с наличием количества, и оно связано с отсутствием понимания учёными происходящих в мироздании процессов. Для описания нейтрино и антинейтрино используется уравнение с двухрядными матрицами Паули (уравнение Вейеля), либо уравнение Дирака, с расщеплением на два независимых уравнения [34, с. 355]:
| (100) |
Так как масса покоя для нейтрино и антинейтрино равна нулю, то отсюда следует вывод об их движении со скоростью света, что соответствует необходимости представления функций Ψ через электромагнитные составляющие, так как с такой скоростью не могут двигаться объекты с иным представлением. О связи функций Ψ с вероятностью также речи быть не может из-за постоянства скорости света. При этом, мы видим, что отличий между первой и второй парой в системе (100) только в обозначении функций. При этом мы не можем оставить прежние обозначения функций, отражающих составные объекты, так как при отсутствии массы покоя происходит преобразование из корпускулярного вида в волновой вид. Это конечно подразумевает иное взаимодействие составных объектов, иначе бы не было изменений. Собственно изменения касаются перехода от корпускулярного представления (потенциальная энергия) в волновое представление (кинетическая энергия), и наоборот. Это по нашей теории в соответствии с общей формулой Мироздания (1) интерпретируется через смену закономерностей за счёт умножения на мнимую единицу. На основании наших рассуждений с учётом сокращения видов функций Ψ в одном уравнении до двух (Ψ1 и Ψ2, или Ψ3 и Ψ4), мы можем представить второе и четвёртое уравнение в системе (100) в виде:
| (101) |
Сокращение функций до двух (Ψ1 и Ψ2, или Ψ3 и Ψ4) означает отсутствие связи через массу покоя, а наличие двух функций в уравнении характеризует необходимость наличия в объекте противоположностей. Сократив на постоянную Планка ћ, и умножив на (–i), что означает переход в противоположную систему наблюдения, мы получим:
| (102) |
Иными словами, мы имеем два идентичных уравнения, которые могут только отличаться через функции. Вид уравнений (102) соответствует виду усовершенствованных уравнений Максвелла (75). Следовательно, если исходить из усовершенствованных уравнений Максвелла (75), то для получения идентичности мы можем выразить функции Ψ следующим образом:
| (103) |
Иными словами, мы получаем физические аналоги реализаций функций Ψ1 и Ψ2, а также Ψ3 и Ψ4, выраженных через реальные электромагнитные составляющие по (75) с учётом констант электрической и магнитной проницаемости, то есть состояния среды. Это означает, что усовершенствованные уравнения Максвелла отражают реальные объекты в виде электронных и мюонных нейтрино и антинейтрино. Собственно, это объясняет эффект аннигиляции электрона и позитрона, которые описываются системой уравнения Дирака с получением фотонов, тем что взаимодействие усовершенствованных уравнений Максвелла даёт электромагнитную волну по (76). Это происходит на основе взаимодействия электронных и мюонных нейтрино (антинейтрино). Кроме того, мы имеем физический смысл различий между электронными нейтрино и мюонными нейтрино за счёт констант электрической и магнитной проницаемости без выдумывания левой и правой материи. При этом наличие антинейтрино вытекает из комплексно сопряжённого представления по уравнениям (75). По сути, можно считать, что в нейтрино за счёт наличия мнимой единицы заложено направление преобразования компоненты напряжённости поля от координаты длины в координату времени. Отрицательный знак мнимой единицы в уравнении характеризует антинейтрино и связан с обратным преобразованием координаты времени в координату длины. Отсутствие мнимой единицы не позволяет получить разницу в делении на нейтрино и антинейтрино в силу того, что смена направления наблюдения относительно движущейся частицы меняет и представление о правовинтовом или левовинтовом вращении.
Если расписать систему уравнений (98) относительно приравнивания к нулю, и с учётом m0=1/c, а также, что ![]() , то мы получим:
, то мы получим:
| (104) |
С учётом умножения на мнимую единицу будем иметь:
| (105) |
В соответствии с системой Дирака (37), мы должны представить уравнения (105) в частных производных в зависимости аргумента функций по соответствующим переменным в виде:
| (106) |
Понятно, что волновая функция Ам в каждом случае соответствующих производных по координатам длины и времени должна соответствовать волновым функциям Ψ по условию закона сохранения количества при преобразованиях. Действительно видно, что первое уравнение в (106) соответствует волновой функции Ψ2, с соответствующими производными по частям во втором, третьем, и четвёртом уравнениях системы Дирака (37). Разница между функциями только в том, что вместо значения в скорость света (с), присутствует величина (u). И это разница связана с тем, что в системе уравнений Дирака на основе волновых функций, характеризующих вероятность, не учитывается состояние окружающей среды, в отличие от электромагнитных функций. Кроме того, при учёте влияния функции Ψ1 в системе уравнений Дирака, мы должны рассматривать условие смены системы наблюдения на противоположную систему, при котором сумма сменяется на разность, и наоборот. Иными словами, в своей системе уравнений Дирак использовал взаимодействие противоположностей с учётом рассмотрения от соответствующих систем наблюдения при переходе от волновых свойств к корпускулярным свойствам с учётом движения и смене знаков. Таким образом, мы при переходе от Ψ функций к реальным электромагнитным функциям через векторные потенциалы будем использовать те же условия взаимодействия, что применил Дирак. Иными словами, Дирак тоже не обошёлся без представления объектов в зависимости от системы наблюдения. Соответственно замену волновых функций Ψ на векторные потенциалы можно представить в виде:
| (107) |
При этом волновые функции Ψ Луи де Бройля при соответствии уравнению энергии Эйнштейна имеют вид:
![]() , (108)
, (108)
Далее мы можем расписать уравнения на основе векторных потенциалов аналогично системе уравнений Дирака (37) с учётом (107) в виде:
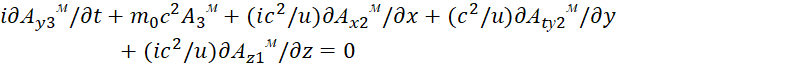 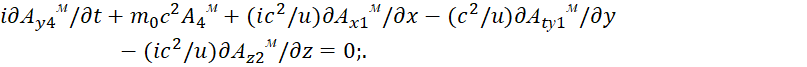 | (109) |
Здесь мы учитываем, что взаимодействие компонент векторных потенциалов при преобразовании и переходе от волновых свойств к корпускулярным свойствам меняется, так как иное означало отсутствие самого взаимодействия. После взятия производных по волновым функциям аналогичным (108) получим вид:
| (110) |
С учётом выражения одних функций через другие для свободной частицы без внешнего электромагнитного поля получаем:
| (111) |
Далее подставляем одни функции вместо других и сокращаем подобные члены:
| (112) |
С учётом сокращения на общую волновую функцию ![]() , имеем энергию в квадрате для частиц с учётом кинетической энергии от противоположности. Для отражения движения без наличия внешних сил, как положительных (позитрон), так и отрицательных (электрон) частиц, имеем формулу энергии Эйнштейна:
, имеем энергию в квадрате для частиц с учётом кинетической энергии от противоположности. Для отражения движения без наличия внешних сил, как положительных (позитрон), так и отрицательных (электрон) частиц, имеем формулу энергии Эйнштейна:
![]() , (113)
, (113)
Таким образом, мы получили переход от волновых свойств к корпускулярным свойствам на основе векторного потенциала Ам. В итоге уравнение (113) соответствует так называемым заряженным элементарным частицам, которые отражают реально движение объектов длины или времени, что мы показали в [9, с. 5-44; 15, с. 32-56]. Здесь есть формирование на основе движения таких объектов со скоростью v замкнутого волнового процесса, с поглощением и излучением по формуле Луи де Бройля, что соответствует формулам (91) и (93). Иной способ получения корпускулярных свойств помимо движения объектов самой среды распространения дал бы независимость пространства и времени от таких объектов, как это получилось с массой покоя и зарядами у физиков, на основе выбранной и придуманной ими системы измерения СИ или СГС.
Как мы отмечали выше, Мироздание основано на замкнутой системе и в этом случае с учётом необходимости взаимодействия противоположностей мы имеем подчинение процессов уравнению гармонического осциллятора (23), с орбитальным движением элементарной частицы (электрон), характеризующей одну противоположность, относительно противоположной частицы с большей массой покоя (протон). Соответственно в этом случае нас интересует вопрос: «Каким образом можно вычислить отношение радиуса орбиты электрона к самому так называемому радиусу электрона?» Это необходимо сделать потому, что вычисление боровских орбит без использования системы измерения СИ или СГС только с применением количественных оценок по нашей теории Мироздания даёт парадокс. Так вычисление первой боровской орбиты на основании формулы, применённой Бором (25), даёт по нашей теории с учётом ![]() и теории Дирака
и теории Дирака ![]() значение:
значение: ![]() . Иными словами, приходим к тому, что первая боровская орбита меньше постоянной Планка.
. Иными словами, приходим к тому, что первая боровская орбита меньше постоянной Планка.
Поэтому будем определять значение боровских орбит исходя из равенства электрической и магнитной силы, как мы это сделали в [35, с. 10-37]. С этой целью необходимо вспомнить формулу отношения магнитной силы к электрической силе при взаимодействии одинаковых точечных зарядов (e) в виде [8, с. 118-119]:
![]() , (114)
, (114)
Такое отношение для вращающегося электрона вокруг протона связано с тем, что мы имеем симметрию в противоположностях, которая обусловлена законом сохранения количества в противоположностях. При этом противоположные частицы в противоположностях имеют одинаковую скорость по отношению к абсолютной системе отсчёта, и если в одной системе наблюдения мы имеем электрон, то в противоположной системе наблюдения он будет интерпретироваться как антипротон, и наоборот. Иное исключает наличие противоположностей и симметрию с учётом закона сохранения количества в мироздании. По (114) отношение магнитной силы определяется значением скорости, а в противоположности это значение длины, характеризующей пространственное искривление, что определяет значение электрической силы и произведение этих величин инвариантно в любой системе координат. В условиях статики это значение в (114) должно определять отношение радиусов электрона и первой боровской орбиты в противоположной системе наблюдения. С этой целью необходимо иметь преобразование значения скорости в параметр длины среды распространения, аналогично тому, как поступил Бор. При этом соответственно используются значения констант электрической и магнитной проницаемости с учётом обратно-пропорциональной связи длины и скорости (последняя формула в (26)). Отсюда формулу (114) с учётом ![]() мы должны представить в виде:
мы должны представить в виде:
![]() , (115)
, (115)
Здесь мы учитываем, что в отличие от системы СИ у нас отношение ![]() . Это связано с тем, что в системе СИ не учитывается различие констант электрической и магнитной проницаемости на скорость света как противоположностей по аналогии с длиной и временем. Это означает парадокс, так как отличие только количественное. Указанное это отличие, связанное с системами измерения не позволяет характеризовать пространственно-временное искривление среды по СТО и ОТО Эйнштейна. Кроме того, в данном случае длина с учётом последнего уравнения в (26) рассматривается как величина, соответствующая длине окружности, по которой осуществляется взаимодействие. Поэтому, чтобы перейти к отношению радиусов мы должны учесть различие h2 от
. Это связано с тем, что в системе СИ не учитывается различие констант электрической и магнитной проницаемости на скорость света как противоположностей по аналогии с длиной и временем. Это означает парадокс, так как отличие только количественное. Указанное это отличие, связанное с системами измерения не позволяет характеризовать пространственно-временное искривление среды по СТО и ОТО Эйнштейна. Кроме того, в данном случае длина с учётом последнего уравнения в (26) рассматривается как величина, соответствующая длине окружности, по которой осуществляется взаимодействие. Поэтому, чтобы перейти к отношению радиусов мы должны учесть различие h2 от ![]() на
на ![]() , что было учтено и Бором. При этом устойчивое состояние протона достигается за счёт максимума по спектру излучения, которое отличается от среднего значения в соответствии с формулой Планка на коэффициент 4,965. Отсюда отношение радиуса первой боровской орбиты rбо к радиусу электрона rэ будет определяться в виде:
, что было учтено и Бором. При этом устойчивое состояние протона достигается за счёт максимума по спектру излучения, которое отличается от среднего значения в соответствии с формулой Планка на коэффициент 4,965. Отсюда отношение радиуса первой боровской орбиты rбо к радиусу электрона rэ будет определяться в виде:
![]() , (116)
, (116)
В классике квантовой механики также проведены расчёты отношения радиуса первой боровской орбиты к радиусу электрона с учётом единиц измерения. При этом радиус электрона равен величие:
![]() , (117)
, (117)
Радиус первой боровской орбиты равен:
![]() , (118)
, (118)
В этом случае имеем:
![]() , (119)
, (119)
Кроме того, если сделать пересчёт при использовании постоянной тонкой структуры, то получим ![]() и
и ![]() Их отношение даёт значение
Их отношение даёт значение ![]() .
.
Иными словами, в классической квантовой механике получается практически аналогичный результат. Однако этот результат получен без учёта параметров среды распространения, таких как константы электрической и магнитной проницаемости, что говорит об отсутствии изменения самой среды и его применения как переносчика взаимодействия.
При этом значение заряда q = е = 1,602176487∙10‒19 Кл противоречит уравнению энергии Эйнштейна, где под заряд нет энергии и ![]() . Следовательно, вычисление первой боровской орбиты на основе системы измерения СИ дало хорошие результаты в результате подгонки за счёт выбора соответствующих единиц измерения. В системе СГС константы электрической и магнитной проницаемости вообще равны единице.
. Следовательно, вычисление первой боровской орбиты на основе системы измерения СИ дало хорошие результаты в результате подгонки за счёт выбора соответствующих единиц измерения. В системе СГС константы электрической и магнитной проницаемости вообще равны единице.
Иными словами, среда распространения в системе единиц измерения, утверждёнными физиками, ‒ это некая «однородная» субстанция не подчиняющаяся СТО и ОТО Эйнштейна. Кроме того, введённые искусственно системы измерения СИ и СГС привели в итоге к обоснованию чёрных дыр из-за радиуса Шварцшильда, кварков и глюонов из-за дробности электрических зарядов, которые выражают энергию взаимодействия.
Таким образом, мы получили не только теоретическое подтверждение связи корпускулярных и волновых свойств с учётом симметрии законов физики в противоположностях, но смогли с помощью нашей теории объяснить и вычислить практические результаты. Это касается аномальных магнитных моментов протона и электрона, разницы масс протона и электрона и отношения первой боровской орбиты к радиусу электрона без парадоксов. Отметим, что ни одна теория даже близко не подошла к решению парадоксов, и физики, поэтому использовали подгонку под результат с элементами чудес.
.png&w=384&q=75)
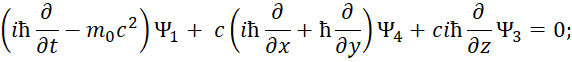
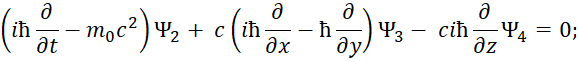
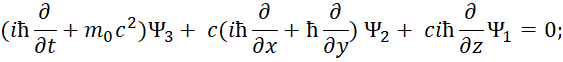
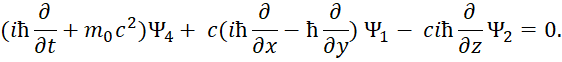
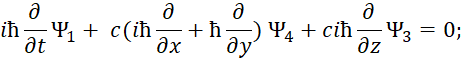
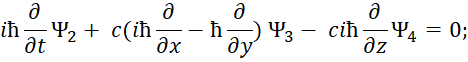
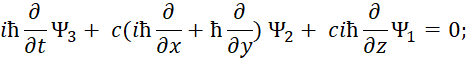
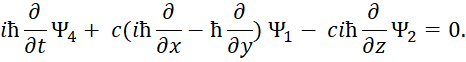
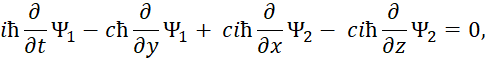
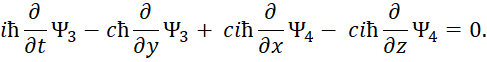
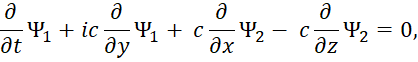
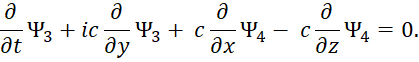
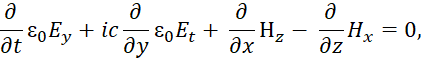
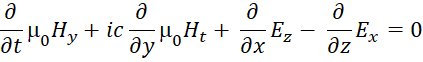
.png&w=640&q=75)