Сравнительный анализ основных алгоритмов поиска пути в играх

Введение

Поиск пути в играх – это процесс нахождения оптимального маршрута для перемещения объекта от одной точки к другой, с учётом различных препятствий, условий окружающей среды и заданных целей. Задача поиска пути является важным элементом в реализации механик, связанных с перемещением по миру, будь то исследование открытого пространства, прохождение уровней или взаимодействие с другими объектами и персонажами. Разработчики используют разнообразные алгоритмы поиска пути для создания более реалистичного и динамичного опыта, а также для эффективного использования ресурсов системы. В этом контексте важно понимать, какие алгоритмы поиска пути наиболее эффективны, в зависимости от размера и сложности игрового мира, а также от требований ко времени отклика и точности решений.

Основные алгоритмы поиска пути

1. Алгоритм A*

Это один из самых популярных и эффективных алгоритмов для поиска пути. A* использует эвристическую функцию для оценки стоимости пути от начальной точки до цели, комбинируя расстояние от текущей точки до начальной (g) и предполагаемое расстояние до цели (h). Алгоритм гарантирует нахождение оптимального пути, если эвристика является допустимой (не переоценивает расстояние до цели).

Преимущества:

Обеспечивает оптимальный и относительно быстрый путь. Широко используется в играх для поиска путей в больших и сложных мирах.

Недостатки:

Может быть ресурсоёмким при больших размерах карты или сложных задачах.

Алгоритм A* ориентируется на два параметра:

• g(n) – фактическая стоимость пути от начальной точки до текущей клетки/узла n.
• h(n) – эвристическая оценка оставшегося пути от текущей клетки до целевой.

Таким образом, каждый узел имеет суммарную оценку f(n), которая вычисляется как: f(n)=g(n)+h(n).

Алгоритм работает следующим образом (рис. 1):

1. Начинаем с начальной точки и добавляем её в открытый список.
2. Извлекаем узел с наименьшей оценкой f(n) из открытого списка.
3. Если этот узел является целевым, путь найден.
4. Для каждого соседнего узла: если сосед не был посещён или найден более короткий путь, обновляем его стоимость g(n), а также пересчитываем f(n); добавляем соседний узел в открытый список, если он ещё не был там.
5. Повторяем процесс, пока не найдём путь или не исследуем все возможные узлы.

Рис. 1. Визуализация работы алгоритма A*

2. Алгоритм Дейкстры

Алгоритм Дейкстры находит кратчайший путь от одной точки до всех остальных точек в графе без использования эвристики. Он всегда выбирает наименьшую стоимость пути на каждом шаге и расширяет исследуемую область.

Преимущества:

Обеспечивает оптимальный путь, если граф не содержит отрицательных весов. Хорошо подходит для поиска кратчайшего пути в графах без заранее известной цели.

Недостатки:

Менее эффективен, чем A*, если требуется найти путь только до одной цели, так как алгоритм вычисляет пути до всех точек.

Алгоритм работает следующим образом (рис. 2):

1. Инициализация:

• Алгоритм начинается с выбора стартовой вершины, которой присваивается стоимость пути, равная нулю.
• Для всех других вершин графа устанавливается бесконечность в качестве стоимости пути, так как они ещё не были достигнуты.
• Составляется список или очередь с приоритетом для хранения вершин, которые нужно обработать. В начале только стартовая вершина находится в списке.

2. Выбор вершины с минимальной стоимостью:

• На каждом шаге алгоритм выбирает вершину с наименьшей стоимостью пути среди ещё не обработанных вершин.
• Для этой вершины алгоритм проверяет все её соседние вершины и пытается обновить их стоимости путём прохождения через текущую вершину. Если путь через текущую вершину оказывается более коротким, чем уже найденный для соседней вершины, то обновляется стоимость этой вершины.

3. Обработка всех вершин:

• Когда все соседние вершины обработаны, текущая вершина помечается как обработанная, и она больше не будет участвовать в дальнейшем процессе.
• Алгоритм продолжает выбирать вершины с минимальной стоимостью и обновлять соседей, пока все вершины графа не будут обработаны или пока не будет найден путь к целевой вершине.

4. Завершение:

• Как только все вершины были обработаны или когда найден путь к целевой вершине (если мы ищем кратчайший путь только к одной вершине), алгоритм завершает выполнение.

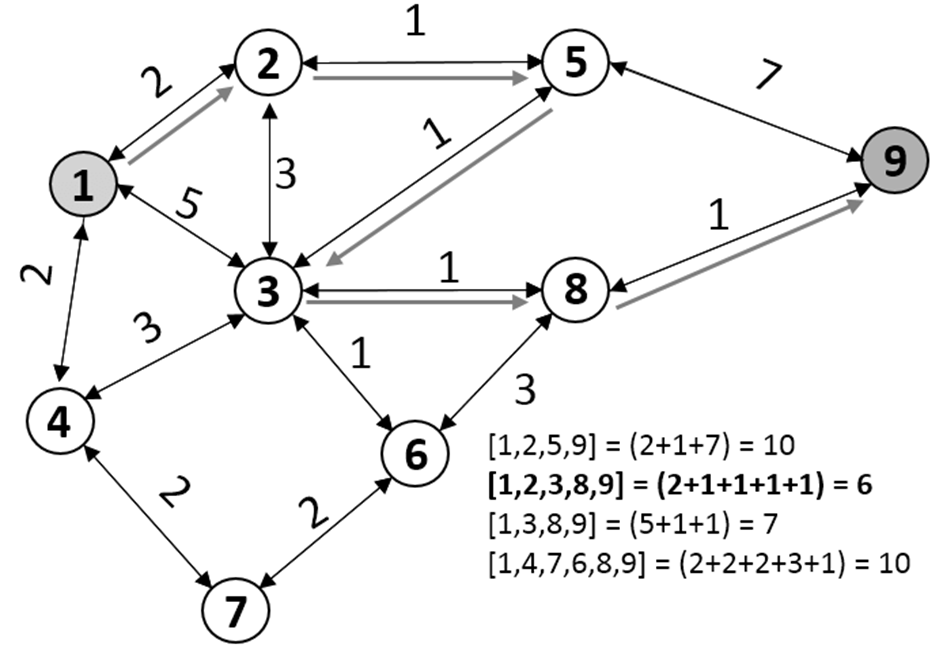
Рис. 2. Визуализация работы алгоритма Дейкстры

3. Волновой алгоритм

Волновой алгоритм используется для поиска кратчайшего пути с равными затратами на переход между клетками. Алгоритм начинается с исходной точки и «распространяет волну» на соседние клетки, постепенно заполняя все возможные клетки. Процесс продолжается, пока не будет достигнута целевая точка, после чего путь восстанавливается, следуя от цели к началу.

Преимущества:

• Простота реализации.
• Гарантирует нахождение кратчайшего пути в равномерных пространствах.
• Эффективен для небольших карт и регулярных пространств.

Недостатки:

• Неэффективен на графах с переменными затратами или сложными структурами.
• Требует значительных ресурсов на больших картах.
• Не использует эвристики для ускорения поиска, что снижает его производительность на больших картах.

Алгоритм работает следующим образом (рис. 3):

1. Инициализация:

• Начинаем с исходной клетки или точки старта и ставим её в очередь.
• Помечаем её как посещённую и присваиваем стоимость пути для этой клетки, равной нулю.
• Все остальные клетки изначально имеют неограниченно большую стоимость (или помечены как непосещённые).

2. Распространение волны:

• Извлекаем клетку с наименьшей стоимостью из очереди.
• Для этой клетки исследуем её соседей (вверх, вниз, влево, вправо или по диагонали, в зависимости от условий задачи).
• Каждому соседу присваиваем стоимость, равную стоимости текущей клетки + 1 (если шаги одинаковые по стоимости).
• Добавляем непосещённые соседние клетки в очередь и помечаем их как посещённые.

3. Продолжение поиска:

• Повторяем процесс, пока не достигнем целевой клетки или не исследуем все возможные клетки.
• Когда цель будет достигнута, восстанавливаем путь, двигаясь от цели к начальной точке, используя информацию о предыдущих клетках (которые ведут к целевой).

4. Завершение:

• Алгоритм завершится, когда целевая клетка будет посещена или если все возможные клетки будут исследованы, и не найдена цель (в случае отсутствия пути).

Рис. 3. Визуализация работы волнового алгоритма

Сравнение производительности в играх

Для сравнения рассмотрим ключевые аспекты производительности этих алгоритмов, такие как время выполнения, память, гарантии оптимальности пути и подходящие сценарии использования (рис. 4).

1. Алгоритм A*

Время выполнения:

• Время работы алгоритма A* зависит от выбранной эвристики и структуры карты. В худшем случае его сложность – O(b^d), где b – это максимальное количество потомков в узле, а d – глубина дерева поиска. Если эвристика является «достаточно хорошей», A* может быть значительно быстрее, чем другие алгоритмы, так как сокращает количество проверяемых узлов. Эвристики, такие как евклидово или манхэттенское расстояние, ускоряют выполнение алгоритма.

Память:

• A* использует память для хранения всех открытых и закрытых узлов. Это может быть значительным в случае больших карт, что делает алгоритм довольно требовательным к памяти.
• В худшем случае (если эвристика не даёт хорошего приближения) алгоритм может потребовать хранения множества узлов.

Оптимальность:

• A* гарантирует нахождение оптимального пути, если эвристика является допустимой (то есть не переоценивает расстояние до цели).

Подходит для:

• Игры с открытым миром (например, RPG, шутеры с открытым миром) и стратегии, где требуется динамичный поиск пути.
• Сложные игровые миры с перемещением в 2D или 3D, где важно иметь оптимальный путь при большом количестве возможных путей.

2. Алгоритм Дейкстры

Время выполнения:

• Время работы алгоритма Дейкстры зависит от структуры данных, используемых для хранения графа. Если используется очередь с приоритетом (min-heap), сложность составит O((E + V) log V), где E – количество рёбер, а V – количество вершин. В случае графов с большим количеством рёбер и вершин, алгоритм может быть достаточно медленным, так как он исследует все возможные пути от источника.

Память:

• Дейкстра требует хранения информации о стоимости пути для каждой вершины, что требует значительных вычислительных ресурсов, особенно на больших картах.

Оптимальность:

• Дейкстра всегда находит оптимальный путь, так как он гарантирует, что путь, найденный первым, будет кратчайшим. Однако, в отличие от A*, алгоритм Дейкстры не учитывает цель, что делает его менее эффективным при поиске пути от одной точки до конкретной цели.

Подходит для:

• Стратегии, где нужно найти кратчайшие пути от одной точки до всех остальных. Реалистичные симуляции или анализ больших сетей, где необходимо вычислить кратчайшие пути для множества точек (например, навигация по городам).

3. Волновой алгоритм

Время выполнения:

• Время работы волнового алгоритма пропорционально числу клеток на карте, т. е. O(n * m), где n и m – размеры карты (или графа). Это означает, что алгоритм работает за линейное время относительно общего числа клеток. Алгоритм достаточно быстрый для карт малых и средних размеров, но может стать медленным для карт большого размера.

Память:

• Волновой алгоритм использует память для хранения информации о том, на каком «этапе» находится каждая клетка. Память используется пропорционально числу клеток, что делает алгоритм менее требовательным, чем A* или Дейкстра.
• Память также зависит от размера карты, но, в целом, алгоритм экономичен по сравнению с другими методами.

Оптимальность:

• Волновой алгоритм находит оптимальный путь, если все рёбра графа имеют одинаковую стоимость.

Подходит для:

• Лабиринты, головоломки или платформеры, где карта имеет регулярную структуру и одинаковые затраты на перемещение.
• Игры с небольшими или статичными картами, где пути не меняются часто.

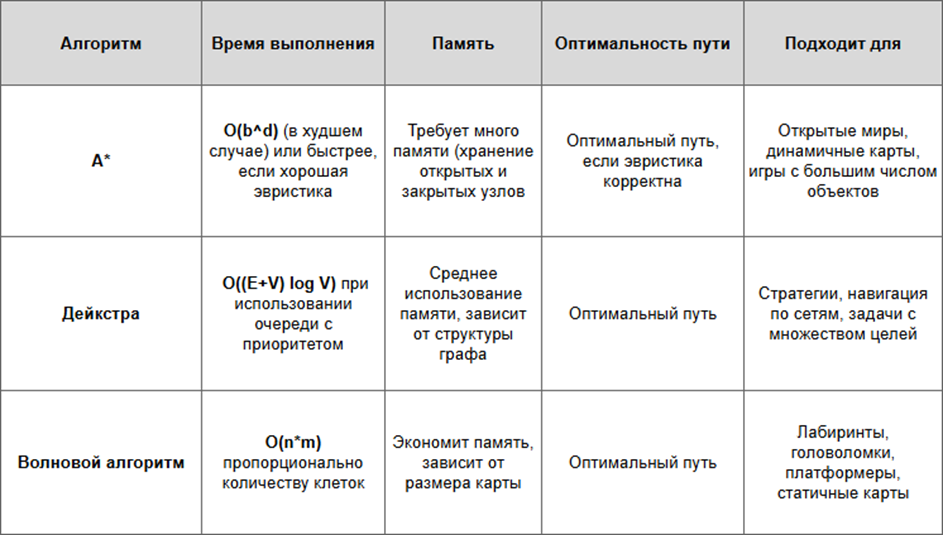
Рис. 4. Сравнение алгоритмов поиска пути

Заключение

В выборе алгоритма поиска пути для игр важным фактором является баланс между производительностью, оптимальностью пути и требованиями к вычислительным ресурсам. На основе проведённого сравнения можно выделить несколько ключевых выводов, которые помогут выбрать наиболее подходящий алгоритм в зависимости от особенностей игры.

Алгоритм A* является наиболее универсальным и эффективным для динамичных и открытых миров, где требуется быстрое и точное нахождение кратчайшего пути, особенно при наличии сложных препятствий и разнообразных затрат на передвижение. Он идеально подходит для игр с большим количеством объектов, таких как ролевые игры или шутеры с открытым миром, но его производительность может снижаться на очень больших картах из-за высокого потребления памяти.

Алгоритм Дейкстры идеально подходит для задач, где необходимо найти кратчайшие пути от одной точки ко всем остальным, что делает его отличным выбором для стратегий и сетевых приложений, где анализируются все возможные маршруты или пути. Однако, из-за отсутствия эвристики, алгоритм может быть медленнее и менее эффективным, чем A*, особенно при поиске пути только до одной цели.

Волновой алгоритм – это простой и быстрый метод, особенно подходящий для небольших карт с одинаковыми затратами на передвижение, как в случае с головоломками, лабиринтами или платформерами. Он значительно экономит ресурсы и требует минимального использования памяти, но ограничен в применении и не подходит для сложных динамичных карт с переменными затратами.

Таким образом, для открытых миров и динамичных игр с высокими требованиями к производительности и оптимальности, лучше всего использовать A*, для анализов больших графов или сетей – Дейкстру, а для простых карт с одинаковыми затратами – Волновой алгоритм. Выбор конкретного алгоритма всегда зависит от специфики задачи и особенностей игрового процесса, и знание их сильных и слабых сторон поможет создать оптимальный опыт для игроков.