Длинные линии (ДЛ) относятся к цепям с распределенными параметрами, где параметры r, L, С распределены и неотделимы один от другого.
ДЛ – это система проводов, у которых длина l соизмерима с длиной волны λ, распространяемых вдоль линии электромагнитных колебаний или значительно больше ее.
При передаче по линии ЭМ энергии, в силу конечной скорости распространения энергии с < ∞ изменение напряжения на нагрузке U2 будет происходить с запаздыванием относительно изменения напряжения на входе U1 на время tз равное tз = l/c.
Между напряжениями U2 и U1 возникает сдвиг фаз δ = ω tз, который зависит от длины линии и от длины волны сигнала, т. е. от его частоты:
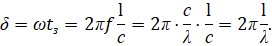
Таким образом, является ли данная линия цепью с распределенными параметрами зависит от соотношения l/λ.
Практически линию считают цепью с распределенными параметрами, если ее длина примерно равна длине волны передаваемого сигнала, т.е. l ≥ 0,1 λ. Линию (любой кабель) при этих условиях называют длинной линией.
При использовании длинных линий на высоких частотах, когда ωL0 >> R0 и ωC0 >> G0, значения R0 и G0 можно принять равными нулю. Такие линии называют линиями без потерь.
На конце линии выделяют следующие режимы работы зависимости от нагрузки Zн:
- линия с разомкнутыми выходными зажимами, Zн = ∞ (режим холостого хода);
- линия с замкнутыми накоротко выходными зажимами Zн = 0 (режим короткого замыкания);
- подключение к линии реактивной нагрузки Zн = ± jX;
- подключение к линии согласованной нагрузки Zн = ZВ;
- подключение к линии несогласованной нагрузки Zн ≠ ZВ.
В режиме холостого хода коэффициент отражения по напряжению равен единице:
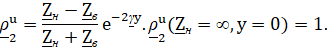
Амплитуды падающей и отраженной волн напряжения равны и совпадают по фазе.
На конце линии образуется пучность напряжения.
Амплитуды падающей и отраженной волн тока равны и находятся в противофазе. На конце линии образуется узел тока: ρi-2-=-1. → I2 = Im.п – Im.о = 0.
С течением времени распределение действующих значений напряжения и тока вдоль линии остается неизменным.
Вышеописанный режим колебаний называют режимом стоячих волн.
Стоячие волны являются результатом сложения падающей и отраженной волн с равными амплитудами. В этом режиме в линии имеются точки, где амплитуда колебаний всегда равна нулю (узлы напряжения или тока) и точки, где амплитуда колебаний максимальна и вдвое больше амплитуды падающей волны (пучности напряжения или тока).
В узлах фазы противоположны и амплитуда суммарной волны равна нулю. Узлы (нули) и пучности (максимумы) не меняют своего положения, (волны напряжения и тока с течением времени не перемещаются вдоль линии, а совершают колебания вблизи точек максимумов). Отрезки ДЛ длиной кратной λ/4 энергетически между собой не связаны.
Входное сопротивление линии зависит от длины линии l и реактивно, т.е. потери энергии отсутствуют:
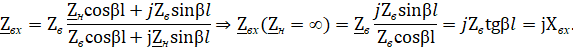
Следовательно, изменяя длину линии можно имитировать емкостное или индуктивное сопротивления. В режиме короткого замыкания амплитуды, падающей и отраженной волн напряжения равны и находятся в противофазе. На конце линии образуется узел напряжения.
Коэффициент отражения по току равен единице. Амплитуды падающей и отраженной волн тока равны и совпадают по фазе. На конце линии образуется пучность тока. Изменяя длину линии, также можно имитировать емкостное или индуктивное сопротивления, а также колебательные контура. Входное сопротивление согласованной линии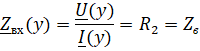 
активное, равно волновому сопротивлению и не зависит от длины линии.
В линии без потерь при резистивной несогласованной нагрузке существует режим смешанных волн.
При нагрузке линии на индуктивность или емкость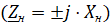 
также образуются стоячие волны, как и в режимах холостого хода и короткого замыкания.
Реактивный элемент, подключаемый к линии в качестве нагрузки, можно заменить эквивалентным отрезком линии, входное сопротивление которого равно сопротивлению реактивного элемента.
Компьютерная система схемотехнического моделирования Micro-Cap позволяет с помощью экспериментов на компьютере провести широкие исследования распределения напряжений и токов в длинных линиях без потерь в режиме бегущих и стоячих волн при различных видах нагрузки: коротком замыкании линии, при холостом ходе, при активной и реактивной нагрузке.
.png&w=640&q=75)
