Виды и формы движения в неоклассической физике

Неоклассическая физика понимает под видами движения перемещения механических систем (объектов, тел) в Пространстве с различной интенсивностью, показателем которой может быть скорость, ускорение, либо ускоренность.

Под формами движения неоклассическая физика понимает траекторию перемещения механических систем (объектов, тел) в Пространстве либо прямолинейно, либо криволинейно.

Равномерное прямолинейное движение

Этот вид и форма движения характеризует перемещение механических систем (далее по тексту МС) с постоянной скоростью без каких-либо отклонений от прямолинейной траектории.

Равномерное прямолинейное движение, это всегда есть результат воздействия на МС либо внутренней, либо внешней силы, которая описывается уравнением:

F = m * u, (1)

Где:

m – масса МС;

u = ℓ/t – скорость перемещения МС в Пространстве;

ℓ – путь пройденный МС за время t.

Если на механическую систему воздействует только одна сила, то она всегда движется прямолинейно в направлении действия этой силы. Если на МС воздействует одновременно несколько разнонаправленных сил, то она двигается всегда только прямолинейно в направлении результирующего вектора геометрического сложения всех воздействующих на неё сил. В зависимости от исследовательских задач сила может быть, как векторной, так и скалярной величиной.

В любом случае, движение МС, это всегда результат воздействия на неё той или иной силы. Без такого воздействия МС остаётся неподвижной, или иначе, в состоянии покоя, в формулировке классической физики.

Чтобы равномерное прямолинейное движение было реализовано неограниченно долго во времени МС должна постоянно получать внешний или внутренний импульс движения, который определяется из выражения:

Y = (m*u) / t, (2)

Где:

t – одна единица времени использованная в определении скорости.

То есть, в этом случае речь идет о мгновенном импульсе, обеспечивающим постоянное равномерное движение в единицу времени.

Этот единичный механический импульс соответствует мгновенной кинергии равномерного прямолинейного движения, то есть, количеству энергии, которое необходимо передать МС при её перемещении на расстояние, которое преодолевает МС за единицу времени:

К = Y * ℓ = [(m*u) / t] * (u*t )= m * u², (3)

Где:

ℓ = u*t – расстояние, которое преодолевает МС двигаясь со скоростью u за время t.

u – постоянная скорость движения МС /1/.

Работа, которую необходимо совершить для реализации равномерного прямолинейного движения, есть произведение мгновенной кинергии на полное время движения МС:

А = К * Т = m * u² * Т = m * u * L = F * L, (4)

Где:

Т – полное время продолжительности равномерного прямолинейного движения в единицах времени использованной в определении скорости;

L – полный путь (расстояние) пройденный МС за время Т;

u – постоянная скорость движения МС.

Итак, мы видим, в отличие от классической физики методология неоклассической физики позволяет вычислять для равномерного прямолинейного движения силу, импульс, мгновенную кинергию и работу, совершаемую при этом МС.

Равномерно ускоренное прямолинейное движение

Равномерно ускоренное прямолинейное движение МС в отличие от движения с постоянной скоростью характеризуется понятием мгновенной силы:

F_мг = m * u_max, (5)

Где:

u_max – мгновенная скорость в конце пути равномерно ускоренного прямолинейного движения МС при u₀=0.

Также равномерно ускоренное прямолинейное движение МС характеризуется средней силой, определяемой из выражения:

F_ср = m * u_ср = m* (u₁ + u₂), (6)

Где:

u₁ – скорость МС в начале пути;

u₂ = u_max – скорость МС в конце пути.

При u₁=0 выражение (6) преобразуется к виду:

F_ср = m * u_ср = m * u_max, (7)

Соответственно, при равномерно ускоренном прямолинейном движении на МС воздействует механический импульс, определяемый из выражения:

Y = F / T = [m*u_max] / T = [m*Δu] / T = m * a, (8)

Где:

Т – полное время равномерно ускоренного прямолинейного движения МС;

а = (u_max – 0)/T = (u₂ – u₁)/Т – ускорение равномерно переменного прямолинейного движения МС.

Кинергия МС в конце пути равномерно ускоренного прямолинейного движения находится из выражения:

К = Y*L = F_max * u_max = m * u_max², (9)

Где:

Y – механический импульс инициирующий движение МС;

L – путь пройденный МС под воздействием механического импульса;

F_max – сила воздействующая на МС в конце пути;

u_max – скорость МС в конце пути;

m – масса МС.

Средняя кинергия равномерно ускоренного прямолинейного движения МС определяется из выражения:

К_ср = (К₂ – К₁) = ΔК, (10)

При К₁=0; К₂=К_max

К_ср = К₂ = mu_max², (11)

Таким образом, при использовании традиционного выражения классической физики среднего значения мгновенной кинергии равно ускоренного прямолинейного движения МС необходимо понимать, что при этом в выражении (11) должна использоваться не средняя скорость процесса, а её максимальное значение в конце пути.

Работа равно ускоренного прямолинейного движения МС в неоклассической физике определяется как произведение средней кинергии процесса на время его продолжительности из выражения:

А = К_ср * T = mu_max² * Т = mu_max * L, (12)

Где:

Т – полное время продолжительности процесса движения;

L – полный путь (расстояние) пройденный МС за время равномерно ускоренного прямолинейного движения.

Особо следует отметить, что длительное движение с ускорением, можно наблюдать только в космических масштабах. В земных условиях механический импульс, это, как правило, кратковременное явление, которое используется либо как источник самого движения, так и изменения его интенсивности во времени. Любое движение начинается с положительного ускорения и заканчивается отрицательным (торможением). Без особой необходимости движение между этими двумя точками, начала и конца движения, как правило, проходит с постоянной (или условно постоянной) скоростью, которое то же требует энергетических затрат. В классической физике этот этап движения, с точки зрения закона сохранения энергии не рассматривался. Это стало доступным только в неоклассической физике. В связи с этим работа полного цикла движения МС рассматривается как сумма работ отдельных этапов движения. Причём завершающий этап, торможение, рассматривается как отрицательная работа, энергию которой при определённых условиях можно вернуть источнику /2/.

Второй принципиально важный момент в анализе динамики движения, это определение мощности движения. В классической физике эта задача решалась через работу. Сначала вычислялась работа, как произведение силы, вычисленной по Второму закону Ньютона, на путь:

А = m * a * L = m * u², (13)

Не трудно видеть, что в этом случае вычислялась максимальная кинергия МС в конце пути при движении с ускорением. Чтобы этого не произошло, и вычислялась бы средняя энергия, длину пути вычисляли для движения с ускорением, что представляется вполне логичным:

L = u² / 2a, (14)

Тогда выражение (13) преобразовывалось к виду:

А = (m*u²) = К_ср, (15)

Причём скорость в этом выражении соответствует максимальной скорости движения с ускорением в конце пути (11), о чём стыдливо умалчивалось.

Затем полученное значение средней кинергии относилось ко времени проведенному МС в пути [7, с. 208]:

N = A / T = [ (m*u²)] / Т = К_ср / Т, (16)

С точки зрения физического содержания, это выглядит как совершенный абсурд. Работа в данном случае вычислена как половина максимальной кинергии в конце пути, которая в этом случае представляет собой среднюю мгновенную энергию процесса движения с переменной скоростью. Иными словами, с физической точки зрения работа в этом случае не вычислялась вовсе, а вычислено среднее значение мгновенной кинергии движения в единицу времени.

Отношение мгновенной энергии к длительности самого процесса движения физического содержания не имеет. Это абстрактное математическое действие, к физическому процессу не имеющее никакого отношения.

Таки образом, мы видим, что уже в фундамент классической физики математики протащили свои виртуальные абстракции. Поэтому в неоклассической физике отсутствует понятие «мощность», как не имеющее физического содержания, вместо него используется понятие «мгновенная энергия» процесса в единицу времени, что, собственно, по своей физической сути и есть мощность движения.

Неравномерно ускоренное движение

В общем виде неравномерно ускоренное движение представляет собой движение с переменным ускорением или ускоренностью во времени:

у` = da / dt

у`` = dу` / dt

у``` = dу`` / dt

И т. д.

Где:

у^\n\ – ускоренность энного порядка;

da – изменение ускорения во времени;

dt – интервал времени в течении которого происходит изменение ускорения или ускоренности, как правило, соответствует единице времени.

В макро процессах этот вид движения может встречаться не далее первого порядка, то есть, переменного ускорения. Высшие порядки переменности характера движения необходимы для анализа процессов эволюции материи, так как позволяют понять эналлизм переменности плотности материи во времени и пространстве, и связанного с её дискретным уменьшением от плотности Планка до плотностей близким к абсолютному вакууму. Поэтому этот вид движения более подробно будет рассмотрен в разделе «эволюция материи» в будущих публикациях.

Формы движения

Прямолинейное движение

Все МС, без какого-либо исключения, в отсутствии каких-либо внешних воздействий на них всегда двигаются в Пространстве только и только прямолинейно. Наглядным примером этому служит движение электромагнитных квантов, которые однажды получив импульс к движению продолжают его бесконечно долго по прямой линии, которая связывает их источник с наблюдателем. Как показывает анализ сверх мощных излучений, расстояние между источником и наблюдателем при этом может составлять квадриллионы св. лет, т. е. условно говоря бесконечность.

Анализ динамики прямолинейного движения рассмотрен выше

Криволинейное движение

В случае внешнего или внутреннего воздействия на МС она может отклониться от прямолинейного движения. В этом случае её движение приобретает форму криволинейного движения, но стремление к прямолинейному движению у неё сохраняется до тех пор, пока не исчерпается энергия импульса, стимулирующего её движение.

В этом случает всегда действует правило центробежной силы, которая пытается вернуть траекторию движения МС к прямолинейной траектории. Направление центробежной силы всегда направлено в противоположную сторону искривления траектории, поэтому утверждение классической физики о центростремительной силе глубоко ошибочно, такой силы в природе не существует.

В неоклассической физике центробежная сила является следствием тангенциальной силы, как результата прямолинейного импульса. При этом прямолинейный импульс криволинейного движения всегда направлен по касательной к его траектории, в то время как центробежная сила всегда направлена по радиусу кривизны в противоположную от его центра сторону (рис.). При этом важно понимать, что самостоятельного, отдельного центробежного импульса в природе не существует. Существует один единственный тангенциальный импульс, которой порождает сначала тангенциальную силу, и лишь спустя определённое время силу центробежную, направленную перпендикулярно тангенциальной силе.

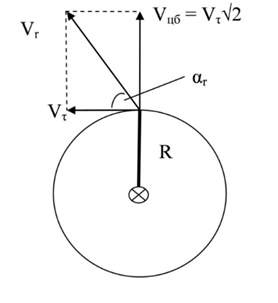
Рис.  Соотношение тангенциальной и центробежной скоростей

Поскольку источником движения МС является тангенциальный импульс прямолинейного движения, то время для формирования центробежной силы отличается от времени необходимого для формирования тангенциальной силы. Этот вывод является результатом анализа механизма передачи энергии движения в перпендикулярном направлении:

, (17)

Где:

t_r – время формирования радиальной (центробежной) силы;

t_τ – время формирования тангенциальной (прямолинейной) силы.

Сила связана с импульсом следующим выражением: F = Y*t. Откуда:

, (18)

Соответственно, угол выхода МС с криволинейной траектории на прямолинейную составит .

Выражение (18) позволяет вычислить, например, соотношение первой (V1) и второй (V2) космических скоростей.

V1 = 7900 м/с

Завершая проведённое исследование можно сделать следующие выводы.

Неоклассическая физика выделяет три вида движения: равномерное с постоянной скоростью, равномерно ускоренное с постоянным ускорением и неравномерное с переменным по времени ускорением; в двух формах: прямолинейном и криволинейном.

Равномерное движение с постоянной скоростью характеризуется отсутствием ускорения и присутствием постоянной силы, как источника движения МС. При этом, для сохранения постоянного движения неограниченно долго в макро МС неизбежные потери движения должны компенсироваться непрерывной последовательностью механических импульсов сообщающих МС необходимую для этого кинергию равную m*u².

Для оценки динамической мощности движения в неоклассической физике используется понятие «мгновенная кинергия (энергия)», поэтому отдельного, самостоятельного понятия «мощность», как это принято в классической физике, не используется.

Работа механической системы в неоклассической физике рассматривается как произведение кинергии на время в течении которого МС находится в этом состоянии. Для равномерного движения с постоянной скоростью кинергия равна m*u². Для равномерно ускоренного движения энергия для вычисления работы равна 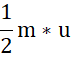, при этом скорость u равна максимальному значению в конце пути с ускорением.

Неравномерно ускоренное движение характеризует ускоренность разных порядков и рассматривается в неоклассической физике в разделе «эволюция материи».

Все МС без исключения, приобретая импульс формирующий их движение, стремятся только и только к прямолинейному движению. Любое отклонение от прямолинейности связано с внешним или внутренним воздействием на МС, отклоняющим её траекторию от прямолинейности. Поскольку единственным источником движения МС при этом остается импульс прямолинейного движения, который в этом случае становится тангенциальным импульсом, то пытаясь вернуть МС к прямолинейному движению, он формирует необходимую для этого центробежную силу, которая всегда направлена по радиусу кривизны траектории от центра в противоположную от направления кривизны сторону. Поэтому в неоклассической физике нет такого понятия как «центростремительная сила», используемое в классической физики, так как в природе такой силы не существует.

Отношение тангенциальной силы (первичной) к центробежной (вторичной) равно , так как время формирования центробежной силы равно , что делает центробежную силу в больше силы тангенциальной, а угол выхода МС с криволинейной траектории на прямолинейную равным , что мы и наблюдаем в технике метания молота олимпийскими чемпионами, так как он даёт возможность, при прочих равных условиях, пролететь молоту максимально возможное расстояние (рис.).

Примечания

/1/ Не трудно заметить, что это выражение (3) практически совпадает с эйнштейновской эквивалентностью массы и энергии, представляющую собой физическую концепцию теории относительности, согласно которой полная энергия физического объекта (физической системы, тела) в состоянии покоя равна его массе, умноженной на размерный множитель квадрата скорости света в вакууме: Е = m*c². То есть, Эйнштейну хватило сообразительности понять, что электромагнитное излучение перемещается в пространстве с постоянной скоростью, и использовать формулу вычисление расстояния для равноускоренного движения не верно, а вот всем остальным это почему-то не понятно. Мало этого предпринимаются попытки доказать, что Эйнштейн ошибся. Так, например, Кочетков А. В., профессор, доктор технических наук ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет» считает: «Нужно говорить, что тело излучает два фотона, которые движутся в противоположных направлениях и имеют суммарную энергию Е = m₀c². При этом каждый фотон имеет энергию Е = m₀c²/2.» (Интернет-журнал «НАУКОВЕДЕНИЕ» Том 7, № 6, ноябрь-декабрь 2015)

Т. е., профессор вполне «обоснованно» считает, что фотон двигается с ускорением. На этом примере мы видим, что современные учёные и специалисты не видят разницы между движением с постоянной скоростью и с ускорением. Именно это непонимание основ классической физики и стало триггером для формирования базиса неоклассической физики.

/2/ На этом явлении основана энергетическая рекуперация торможения МС электрическим двигателем, который в этом случае становится генератором электрической энергии, которая возвращается в систему электроснабжения МС.