Дисциплина «География» представляется в системе современного высшего образования одной из составляющих системы наук о земле. Географическое образование всё больше интегрируется со смежными научными и предметными областями, в числе которых, в обязательном порядке, присутствует математика. Следует также отметить, что «Математика», как дисциплина, находится в тесной связи с другими дисциплинами учебного плана практически всех гуманитарных направлений подготовки бакалавров [1, с.37]. Проведенные психолого-педагогические исследования показывают, что изучение математики студентами различных специальностей и направлений способствует углублению процесса фундаментализации высшего образования, обеспечению профессиональной компетентности, формированию эрудиции и высокого уровня общей культуры у будущего специалиста.
Как правило, математика для студентов гуманитарных направлений изучается на начальных курсах и одной из задач при изучении математики является формирование математических навыков в качестве инструментария для других наук. Помимо этого, согласно исследованиям психологов и многолетнего опыта преподавания, при изучении основных разделов математики у студентов развивается причинно-следственное и творческое мышление, короткая и длинная память, умение ясно излагать свои мысли, способность корректно ставить вопросы и многое другое.
Вместе с тем, надо отметить те сложности, с которыми сталкивается любой преподаватель математики при разработке своего курса для студентов гуманитарных направлений. Часто студенты-гуманитарии, имеют слабую школьную подготовку по математике, основная масса сдавала ЕГЭ по математике для базового уровня. Навыки самостоятельной работы у таких студентов плохо сформированы и, соответственно, особого интереса к математике, как предмету, они не имели еще во время учебы в школе. Поэтому, поступив в вуз, студенты-первокурсники считают этот предмет малоинтересным и ненужным, не понимая о возможности применения изучаемых понятий и объектов в своей дальнейшей практической деятельности. Как следствие, преподаватели часто сталкиваются с чисто психологическим барьером у своих студентов на начальном этапе изучения вузовской математики.
Надо отметить, что математика, как дедуктивная наука, строится таким образом, что все частные результаты выводятся из небольшого числа общих положений (аксиом). Если же и при построении курса сохранять логически последовательную цепочку заключений, то есть использовать формально-логический метод, то следует делать акцент на строгой последовательности, формальной определенности, логической связности излагаемого материала. Это говорит о так называемом академическом стиле, согласно которому изложение материала происходит дедуктивным методом. Несомненно, что такой стиль был и есть приоритетным в преподавании математики основной массы преподавателей вузов. Однако, одно дело, когда характерные для академического стиля моменты: строгая последовательность в изложении, систематичность материала и его формализация используются при обучении студентов математических специальностей и направлений. В данном случае, они обоснованы и весьма полезны. Но для студентов гуманитарных направлений академический стиль приводит к своего рода сложностям. Принципы академического стиля требуют от студентов держать свои мысли в полном соответствии с мыслями преподавателя. Формальное изложение теоретических сведений очень сложно воспринимать и перерабатывать студенту-гуманитарию. Нельзя также забывать о слабой школьной подготовке многих студентов. Малый объем часов, отведенный в учебных планах на изучение математики, также приводит к снижению качества обучения. Результат такого преподавания может быть сведен к нулю. Это означает, что следует искать альтернативные подходы к преподаванию математики для студентов гуманитарных направлений.
В связи с вышесказанным, первостепенной задачей каждого преподавателя математики является повышение мотивации к изучению математики. Для этого необходима тщательно продуманная корректировка содержания дисциплины (нужно отметить, что современные стандарты позволяют проводить подобные корректировки по усмотрению составителя рабочей программы курса).
Данная статья приводит опыт преподавания математики для студентов направлений «География», «Картография и геоинформатика», «Геология», «Экология и природопользование», обучающихся в Волгоградском Государственном университете.
Для всех этих направлений в преподавании математики делался акцент на иллюстрацию изучаемых понятий примерами и приложениями из географии. Основной материал лекционного курса дополняется элементами математического моделирования процессов и явлений, изучаемых студентами выше указанных направлений на профильных предметах. В силу ограниченности часов, отведенных в учебном плане на практические занятия, некоторые задачи, представленные для самостоятельной работы студентов, подобраны так, чтобы показать возможность применения математических знаний в будущей профессиональной деятельности.
Элементы математического анализа изучаются в курсе математики для всех указанных направлений. Этот раздел имеет возможность наглядного использования математических понятий и методов в географии и геологии при изучении темы: «Приложения производной в географии».
Практика показывает, что большинство студентов тяжело воспринимают основные понятия этого раздела, им сложно ориентироваться в многочисленном для них наборе определений и формул, они не проявляют никакого интереса к предмету. Авторский опыт нескольких лет показал, что повышению мотивации к изучению способствует иллюстрация излагаемого программного материала примерами из предметной области.
Покажем примеры применения развитого математического аппарата исследования функции в географии. Отдельным пунктом лекции по теме: «Выпуклость функции. Точки перегиба» рассматривается пример «Аналитическая классификация элементов рельефа на плоскости» [2, с.197].
Пример. Области с мягким рельефом в виде чередования возвышенностей и понижений рисуются на профиле плавной волнистой линией, аналитическое выражение которой можно представить как непрерывную функцию H=H(x). На таком профиле между точками возвышенностей (гребневыми точками) и точками понижений (килевыми точками) выделяются участки с однообразным уклоном – склоны. В пределах каждого склона касательные к графику функции наклонены везде в одну сторону. Это участки монотонного возрастания или убывания функции.
Известно, что уклон профиля в данной точке равен производной высоты по расстоянию, взятой с отрицательным знаком (ось абсцисс при этом предполагается направленной по падению склона):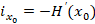 
.
С этой точки зрения склон можно определить как участок профиля, на котором производная высоты по расстоянию везде положительна либо отрицательна.
Рассмотрим широко распространенную в природе форму склона, выпуклого вверх в верхней части и выпуклого вниз в нижней (рис. 1).
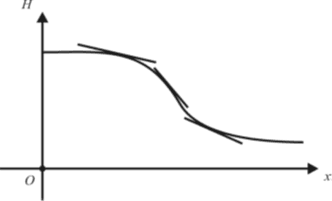
Рис. 1
В нескольких точках склона проведем касательные, наглядно показывающие, как изменяется вдоль склона производная H’= H’(x). Поскольку касательные к графику образуют с положительным направлением оси Ox тупые углы, то функция является убывающей на рассматриваемом промежутке. На выпуклой вверх части склона вторая производная отрицательна: H’’(x)<0, а на выпуклой вниз части склона вторая производная положительна: H’’(x)>0. В точке перегиба от выпуклой вверх части склона к выпуклой вниз части склона вторая производная обращается в нуль: H’’(x)=0.
Таким образом, знак второй производной позволяет различать выпуклые вверх и выпуклые вниз склоны, а ее абсолютная величина указывает степень выпуклости.
Напомним, что вторую производную можно также использовать для нахождения максимумов – гребневых точек (H’’(x)<0) и минимумов – килевых точек (H’’(x)>0).
Как показывает опыт, данный пример вызывает у студентов интерес, они видят наглядное представление изучаемых понятий в предметной области. Многие признаются, что наконец-то увидели смысл изучения математических понятий и теорем.
Для активации учебной деятельности студентов также можно предложить использование в преподавании создания проблемных ситуаций. В математике это несложно сделать через постановку задач с практическим содержанием. Покажем это на примере рассмотрения темы: «Исследование функции с помощью аппарата производной» [2, с.199]. В этом случае для актуализации знаний по изученной теме предлагается рассмотреть решение следующей задачи:
Задача. Область, имеющая четко выраженный горный рельеф, задана аналитически функцией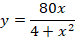 
, описывающей зависимость высоты от расстояния (0 ≤ х ≤ 20).
1) Определить уклон профиля области в точке х0=1.
2) Найти гребневые точки и килевые точки функции H, а также значения функции H в этих точках.
3) Указать участки области с однообразным уклоном (склоны).
4) Определить выпуклые вверх и выпуклые вниз части склонов и точки перегиба.
Решение.
1) Находим
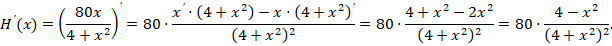
Откуда
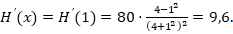
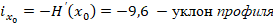
2) Найдем критические точки:
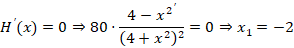и x2=2. В области определения функции Н находится только одна критическая точка x2=2.
Она является точкой максимума или гребневой точкой функции Н. Значение функции Н в этой точке равно: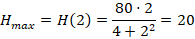 
.
Килевых точек функция не имеет.
3) Участки области с однообразным уклоном характеризуются тем, что на этих участках H’’(x)>0 или H’’(x) <0.
На участке [0; 2) функция Н монотонно возрастает (возрастающий склон); на участке (2; 20] функция Н монотонно убывает (убывающий склон).
4) Определим теперь выпуклые вверх и выпуклые вниз части склонов. Для этого найдем вторую производную функции Н:
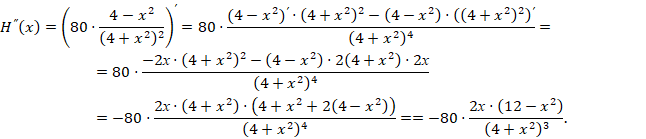
Уравнение H’’(x)=0 имеет в области определения функции Н два корня: x2=0 и x2=2√3 причем на участке (0;2√3) H’’(x) <0, а на участке (2√3;20] H’’(x)>0. Следовательно, на участке (0;2√3) склон является выпуклым вверх, а на участке (2√3;20] – выпуклым вниз.
Далее вычисляем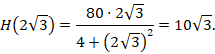 
Точка М(2√3;10√3) является точкой перегиба.
Для наглядности проведенного исследования схематически строится график функции Н=Н(х), характеризующий рассматриваемый в задаче горный рельеф области (рис. 2).
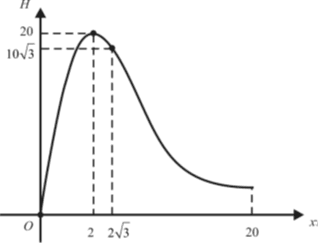
Рис. 2
Это лишь некоторые примеры, которые подобраны для наглядной трактовки приложений производной. Умелое использование подобных приемов обеспечивает развитие познавательного интереса у студентов, более сознательное усвоение материала, позволяет установить межпредметные связи (математика, геология, геодезия и картография), способствует формированию научного мировоззрения, вырабатывает правильную методологию.
