Практические вопросы использования интегральной формулы дисконтирования в постпрогнозный период

Как хорошо известно, для оценки доходообразующих систем наиболее точным и объективным является метод дисконтирования денежных потоков. Классическая формула дисконтирования денежных потоков CF со ставкой дисконта q выглядит следующим образом:

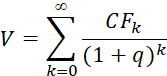, (1)

Как нами было показано [1, с. 31-32], наиболее общий вид выражение для дисконтирования бизнес-систем имеет вид:

, (2)

Но вернемся к этому выражению чуть ниже.

Строго говоря, для использования классической формулы дисконтирования необходимо составить прогноз денежного потока на очень продолжительный период времени (более 80 лет), за пределами которого текущая стоимость денежных потоков бесконечно мала (см. ниже). Очевидно, что такой прогноз невозможно сделать как достаточно подробным, так и достаточно обоснованным, а трудоемкость при этом значительна. Поэтому из практических соображений при построении (прогнозировании) денежных потоков период прогнозирования разбивается на два интервала: прогнозный в течение времени Т и постпрогнозный период:

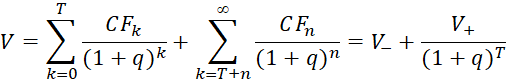, (3)

При этом видно, что дисконтированная стоимость всех денежных потоков в постпрогнозный период определяет стоимость оцениваемого актива в конце прогнозного периода Т:

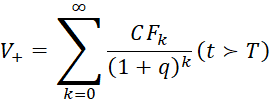, (4)

Анализ и построение денежного потока в прогнозный период и вычисление значения 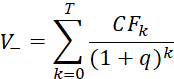мы оставим за рамками настоящего исследования.

Нашей целью является рассмотрение возможностей при оценке денежного потока CF в постпрогнозный период. В литературе существует несколько терминов, определяющих значение , в частности:

• стоимость будущей продажи [2]
• стоимость реверсии [3]
• продленная стоимость [4]

В настоящей статье мы выберем самое короткое определение: стоимость реверсии.

На текущий момент оценка стоимости реверсии является одним из самых слабых мест модели дисконтирования денежных потоков (DCF). Многие аналитики концентрируют все внимание анализу денежного потока в прогнозный период, достаточно легко относятся к оценке стоимости реверсии. При этом они полагают, что при достаточно большом горизонте расчета (прогнозном периоде), как правило, более пяти лет, значительные колебания в оценке значений практически полностью сглаживаются процедурой дисконтирования, держа в уме классический пример из «любимой» книги российских оценщиков [2]. В таблице приведены значения текущей стоимости будущих поступлений FV через различные временные периоды N при ставке дисконта 20%:

Таблица

Видно, что при периоде 20–30 лет текущая стоимость составляет всего 0,6%–2,6% от номинального значения денежных поступлений и существенные колебания будущих поступлений не окажут существенного влияния на итоговое значение дисконтированной стоимости в целом. Однако, реально картина выглядит несколько иначе и значимость стоимости реверсии в конечном результате значительно выше. Во-первых, численное значение стоимости реверсии в несколько раз выше периодических денежных потоков () и, во-вторых, прогнозный период T, как правило, на практике не превышает 5–10 лет.

В результате вольности в оценке стоимости реверсии приводят к существенному искажению результата оценки систем, полученного методом DCF. В подтверждение значимости корректной оценки стоимости реверсии приведем данные о доле текущей стоимости реверсии в совокупной стоимости компаний по некоторым отраслям США [4].

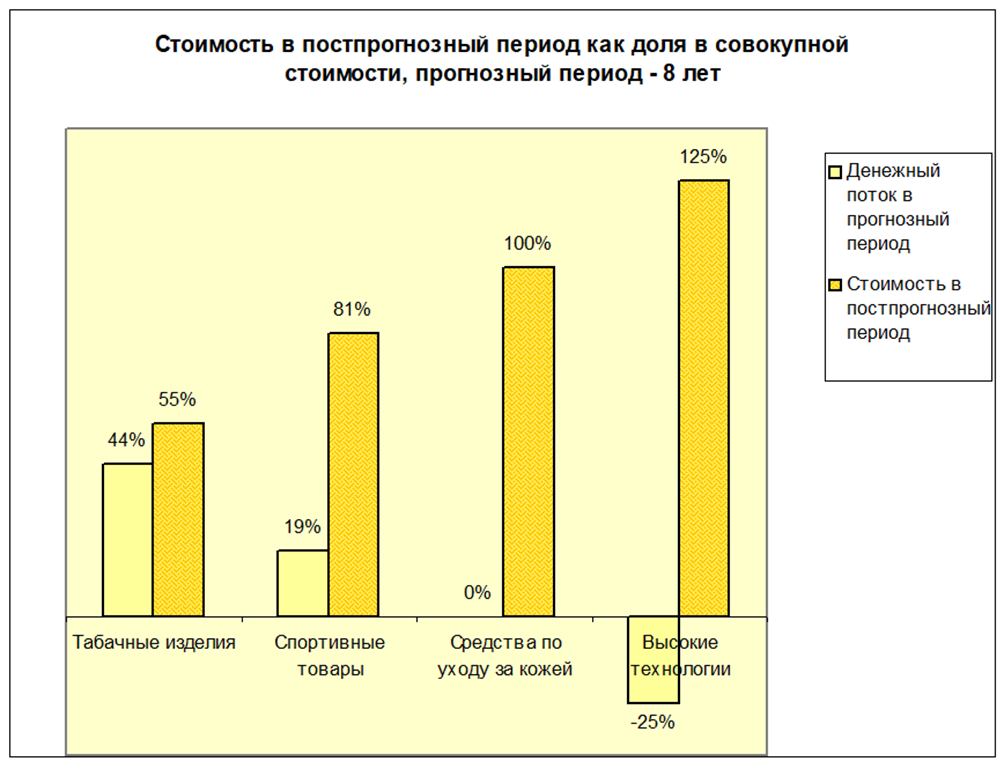
Рис. 1. Источник: данные McKinsey

Рассмотрим существующие, часто используемые на практике, методы оценки стоимости реверсии на примере оценки стоимости действующих компаний:

1. Метод ликвидационной стоимости;
2. Метод стоимости замещения;
3. Метод рыночных мультипликаторов;
4. Метод прямой капитализации;
5. Формула Гордона (метод растущего CF);
6. Формула факторов стоимости.

Первые три метода не основываются на анализе денежного потока в постпрогнозный период, т. е. определяется не на основе формулы 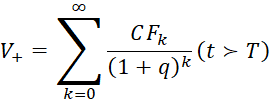, а с использованием других факторов, определяющих стоимостные показатели компании. Использование этих методов часто приводит к ошибочным оценкам стоимости реверсии, поскольку требует очень осмотрительного использования. Остановимся кратко на недостатках этих подходов.

Метод ликвидационной стоимости основан на оценке доходов от продажи всех активов предприятия за вычетом обязательств и всех расходов по реализации в конце прогнозного периода. Очевидно, что если предприятие не собирается закрываться, то мы получим заниженную оценку действующего предприятия , поскольку не будут учитываться нематериальные составляющие бизнеса. Если же отрасль находится в стагнации, то ликвидационная стоимость будет выше действующего предприятия. Кроме того, процедура оценки ликвидационной стоимости достаточно трудоемка, а с учетом низкой достоверности оценок активов и обязательств в конце прогнозного периода, этот метод малополезен и малоинформативен. Аналогичные сложности и болезни присущи методу стоимости замещения.

Метод рыночных мультипликаторов подразумевает оценку стоимости реверсии с использованием мультипликаторов Цена/Выручка (Ц/В), Цена/Прибыль (Ц/П) или Цена/Балансовая стоимость активов (Ц/БА). Поскольку построение денежного потока в прогнозный период непосредственно вытекает из прогнозируемых балансовых отчетов и отчетов о финансовых результатах, то в конце прогнозного периода в нашем распоряжении «автоматически» оказываются такие параметры как выручка, прибыль, балансовая стоимость активов. Поэтому, на первый взгляд, этот метод является очень удобным. Необходимо решить только две проблемы:

• выбрать соответствующий мультипликатор, поскольку рассчитать мы можем только текущее значение мультипликаторов, а их использование в конце прогнозного периода некорректно. Текущее значение мультипликаторов отражает настроения и ожидания инвесторов на настоящий момент, но какие они (настроения и ожидания) будут в конце прогнозного периода, никто не знает и, соответственно, корректно определить значение мультипликатора невозможно.
• мультипликаторы Ц/В, Ц/П и Ц/БА, как правило, определяются по сделкам с акциями аналогичных компаний на фондовом рынке, т. е. с миноритарными (неконтрольными) пакетами акций. Следовательно, для оценки действующего предприятия необходимо внести поправки, связанные со степенью контроля.

Кроме этих чисто «теоретических» вопросов существуют еще как минимум две практические проблемы оценки с использованием мультипликаторов в российских условиях. Во-первых, фондовый рынок России слишком мал и для оценки большинства отечественных предприятий невозможно достаточно обосновано рассчитать мультипликаторы; текущее значение мультипликаторов, рассчитанных на базе зарубежных компаний, как правило, намного выше аналогичных российских показателей. Во-вторых, как показал наш анализ, для отечественных предприятий основных отраслей коэффициент корреляции между рыночной стоимостью компании и прибылью не превышает 0,5, т. е. между прибылью отечественных предприятий и их стоимостью практически нет никакой взаимосвязи. Ну, а о проблеме достоверности балансовой оценки различных показателей любой аналитик знает не хуже нас.

Поэтому наибольшее практическое применение для оценки получили методы, основанные на модели дисконтирования денежных потоков, исходя из выражения 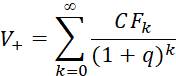. Как мы уже говорили выше, самый «простой» способ долгосрочного прогнозирования CF не работает, поэтому основным инструментом расчета стоимости реверсии стало использование моделей, задающих изменение денежного потока в постпрогнозный период таким образом, с помощью которого бесконечная сумма 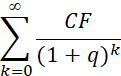сворачивается в конечное число слагаемых.

На текущий момент, основное распространение получили наиболее простые модели, приводящие бесконечную сумму к геометрической прогрессии: модель постоянного CF (прямая капитализация) и модель постоянного роста (формула Гордона). В модели постоянного роста закладывается предположение о постоянном росте денежного потока в постпрогнозном периоде с темпом роста g. В результате для стоимости реверсии мы получаем выражение:

, (5)

Несмотря на заложенные в этой модели недостатки [5], эта модель является наиболее распространенной для оценки стоимости реверсии. Этим она обязана тому, что существует целый класс объектов, для которых результаты DCF, полученные с использованием этой модели, неплохо согласуются с рыночными данными.

Другим часто используемым методом оценки стоимости реверсии является формула факторов стоимости [4], которая оперирует чистой прибылью за вычетом скорректированных налогов NOPLAT и рентабельностью инвестированного капитала ROIC и выглядит следующим образом:

, (6)

Эта формула имеет несколько преимуществ, связанных с использованием всем понятной величины NOPLAT и непосредственным оперированием с основными факторами стоимости: темпом роста прибыли g и рентабельностью основного капитала ROIC. В [4] показана полная эквивалентность модели Гордона и формулы факторов стоимости.

Однако, даже эти, наиболее здравые из используемых, модели оценки стоимости реверсии имеют один существенный недостаток – они в своей основе используют предположение о постоянном бесконечном росте дохода с постоянным темпом роста. Очевидно, что это только первое приближение к реальности. Технические приемы, с помощью которых прогнозный период разбивают на несколько интервалов с различными темпами роста g не решает основной проблемы, указанной выше.

Поэтому хотелось бы поговорить о возможностях построения моделей, более реалистично отражающих изменение денежных потоков в постпрогнозном периоде. Возможности аппарата математического анализа по работе с бесконечными числовыми рядами достаточно ограничены и не очень наглядны. В данном случае интересно посмотреть потенциал концепции непрерывного дисконтирования. Поэтому вернемся к формуле интегрального дисконтирования. При разделении периода прогнозирования на два интервала: прогнозный в течение времени Т и постпрогнозный период выражения для интегрального дисконтирования имеет вид:

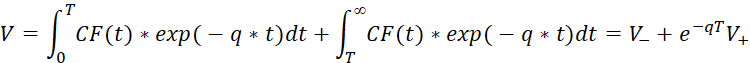, (7)

И, соответственно:

, (8)

Еще раз подчеркнем, что выражения 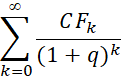и не являются альтернативными, это просто различные альтернативные записи одного процесса. Однако формула позволяет задавать более реалистичные аналитические выражения для изменения функции CF(t) в постпрогнозном периоде, t>T.

Причем, аналитические выражения можно задавать как для функции денежного потока CF(t), так и для темпа роста дохода g(t).

В частности, использование функции позволит «сшить» двух- и трехфазные модели [6, с. 26-29] в одну непрерывную фазу, устранив необъяснимые с теоретической точки зрения скачки.

Например, при оценке новых быстрорастущих компаний приходится использовать многофазные модели, в которых темпы роста скачкообразно снижаются, причем как временные интервалы изменения, так и величину самих изменений темпов роста приходится задавать «руками».

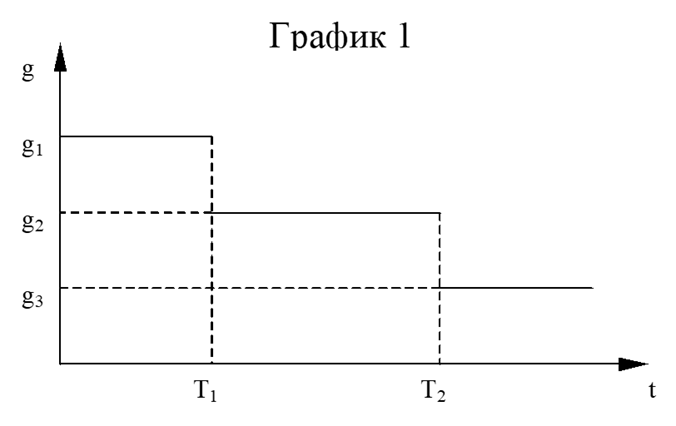
Рис. 2

Интегральная формула дисконтирования для модели постоянного роста имеет следующий вид [6, с. 26-29]:

, (9)

Этот вид формулы дисконтирования позволяет нам использовать более реалистичные модели изменения темпов роста. Например, мы можем для описания постепенного снижения темпов роста со значения в период времени Т до величины в отдаленном будущем использовать следующую функцию g(t):

, (10)

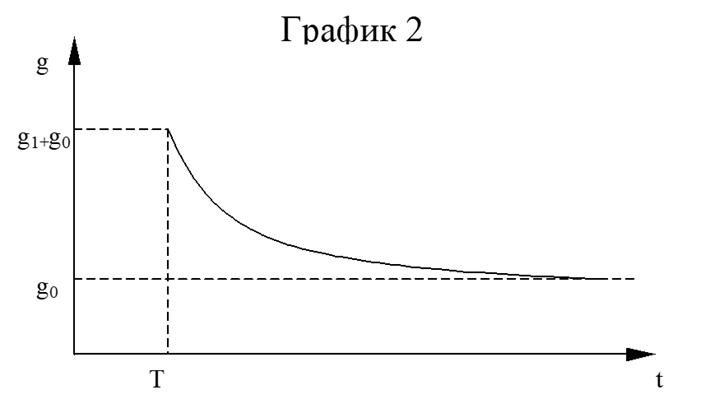
Рис. 3

Подставляя это выражение в формулу для определения стоимости реверсии, получаем:

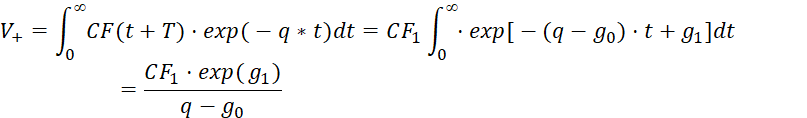, (10)

В качестве второго примера рассмотрим аналитическое выражение для самой функции CF(t). Рассмотрим равномерно убывающую систему:

, (11)

В этом случае для стоимости реверсии получим выражение:

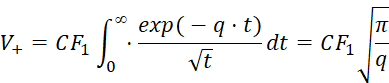, (12)

Мы продемонстрировали на примере двух простейших случаев большой потенциал формулы интегрального дисконтирования. Особенно красиво «сворачивается» несколько многочленов в каждой фазе в модели постоянного роста в конечное выражение (10).

В целом же, для интегральной формулы дисконтирования с учетом некоторых ограничений на функцию CF(t) можно использовать преобразование Лапласа, которое переводит функцию CF(t) в функцию V(q) [7]:

, (13)

Обратное преобразование, определяющее функцию CF(t) как решение интегрального уравнения (13) при заданной функции V(q) дается формулой:

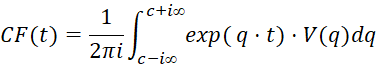, (14)

Мы не ставим себе задачей углубляться в теорию функции комплексной переменной. Важно, что преобразование Лапласа позволяет воспользоваться большим количеством готовых решений для различных функций CF(t). Кроме того, возможно, зная функцию V(q), например, по рыночным данным, определить соответствующее функциональное поведение функции денежного потока.