Exploring counting capabilities of multimodal large language models

1. Introduction

In recent years, artificial intelligence has witnessed remarkable advancements in multimodal large language models (LLMs), which can process and generate content across various modalities such as text, images, and audio. These models, exemplified by systems like GPT-4 and its predecessors, have demonstrated impressive capabilities in understanding context, generating human-like text, and even performing complex reasoning tasks. However, as these models become increasingly integrated into various applications, it is crucial to understand their strengths and limitations across different types of tasks and input modalities.

One fundamental cognitive skill that has yet to be extensively explored in the context of multimodal LLMs is counting. The ability to accurately count objects or occurrences is a basic yet essential task that humans perform effortlessly across various domains. Natural language processing might involve counting the frequency of specific characters or words in a text. In computer vision, it could mean enumerating objects within an image. While these tasks may seem straightforward, they present unique challenges for AI systems, particularly when dealing with different input modalities.

This study aims to evaluate and compare the counting capabilities of multimodal LLMs across two distinct input types: text and images. Specifically, we will assess their performance in counting character occurrences in text and object instances in images. By conducting this comparative analysis, we seek insights into how these models handle quantitative tasks across modalities, potentially uncovering any discrepancies or biases in their performance.

Our research methodology involves creating specialized datasets for both text and image-counting tasks. For the text modality, we utilize a vocabulary of English words, categorized by length, and map specific characters to frequency counts. We leverage existing image datasets in the image domain and employ object detection techniques to generate object frequency data. These carefully curated datasets will serve as the foundation for our evaluation.

We employ a range of multimodal LLMs to assess the models' performance, focusing on the GPT family of models. Our experimental design incorporates two prompt engineering strategies: zero-shot and few-shot learning. This approach allows us to examine how different levels of task-specific guidance affect the models' counting accuracy across modalities.

Through this investigation, we aim to contribute to the growing body of knowledge on multimodal LLMs and provide a unique perspective on their quantitative reasoning capabilities across different input modalities.

The remainder of this paper is structured as follows:

• Section 2 reviews related work on counting tasks in natural language processing and computer vision, providing context for our study.
• Section 3 outlines our methodology, detailing dataset preparation, model selection, and prompt engineering strategies for both text and image-counting tasks.
• Section 4 describes the experimental setup, including procedures for text and image counting tasks and our chosen evaluation metrics.
• Section 5 presents results and analysis, comparing model performance across modalities and analyzing factors affecting counting accuracy.
• Section 6 discusses the implications of our findings, exploring the limitations of current models and considering broader impacts on future development.

2. Related Work

2.1. Counting in Natural Language Processing

Recent advancements in Natural Language Processing (NLP) have brought increased attention to numerical reasoning and counting tasks, particularly with the rise of large language models (LLMs). Wallace et al. [1, p. 5307-5315] conducted pioneering work in this area, probing the numerical understanding capabilities of word embeddings. Their study revealed that standard embeddings naturally possess a surprising degree of numeracy, with character-level embeddings showing even greater precision. This work laid the foundation for understanding how numerical capabilities emerge in NLP models.

Building on this, Thawani et al. [2, p. 644-656] provided a comprehensive survey on number representation in NLP, proposing a taxonomy of numeracy tasks along dimensions of granularity and units. Their work underscores the complexities of teaching machines to understand and generate numerical content, offering insights into various approaches and their effectiveness.

The emergence of powerful language models has further advanced the field of numerical reasoning in NLP. Brown et al. [3, p. 1877-1901] introduced GPT-3, demonstrating its impressive few-shot learning capabilities on various tasks, including arithmetic and complex reasoning. This work showed that scaling up model size can lead to significant improvements in performance across a wide range of NLP tasks. Wei et al. [4] explored the "emergent abilities" of LLMs, noting that certain capabilities, potentially including advanced numerical reasoning, only become apparent at larger model scales. These findings suggest that as models grow in size, they may develop unexpected competencies in areas such as numerical processing.

Prompt engineering has become a crucial aspect of leveraging LLMs for specific tasks, including counting. Kojima et al. [5, p. 22199-22213] investigated zero-shot reasoning strategies, demonstrating how carefully crafted prompts can elicit numerical reasoning from LLMs without task-specific fine-tuning. However, as Mielke et al. [6] discuss, the impact of tokenization on various NLP tasks, including numerical processing, remains a critical consideration. Their work highlights the ongoing debate about the optimal level of text granularity for different NLP tasks, which has implications for how models handle numbers and counting.

2.2. Object Counting in Computer Vision

Object counting in computer vision has evolved significantly over the past decade. Lempitsky and Zisserman [7, p. 1324-1332] introduced a learning-to-count approach using CNNs without explicit object detection. Zhang et al. [8, p. 589-597] developed a Multi-column CNN for crowd counting, showing strong performance in dense scenarios. Object detection methods, which implicitly involve counting, saw advancements with Redmon et al.'s [9, p. 779-788] YOLO system for real-time detection and He et al.'s [10, p. 2961-2969] Mask R-CNN, which added high-quality segmentation capabilities. Du et al. [11, p. 3664-3678] proposed a redesigned multi-scale neural network for crowd counting, introducing a hierarchical mixture of density experts and a new relative local counting loss.

Recent research has focused on reducing annotation requirements and expanding applicability to diverse object types. D'Alessandro et al. [12] introduced AFreeCA, an annotation-free approach using text-to-image models to generate counting datasets for various object categories. This method shows promise in counting diverse objects without relying on specific pre-existing datasets. Tabernik et al. [13, p. 110540] proposed CeDiRNet, a point-supervised learning approach that predicts directional information across images to locate object centers. Their method addresses the challenge of uneven pixel distribution in point annotations and comprises domain-specific and domain-agnostic components, demonstrating improved performance across multiple datasets. These recent works contribute to the development of more efficient and adaptable object-counting systems, capable of handling diverse scenarios with reduced annotation effort.

2.3. Multimodal LLMs and Their Capabilities

Multimodal Large Language Models (MLLMs) represent a significant advancement in AI, capable of processing diverse input types including text, images, and other modalities. Hao et al. [14] pioneered this field by proposing language models as a general-purpose interface for various foundation models, enabling both in-context learning and open-ended generation through a combination of causal and non-causal modeling approaches.

Meta's recent introduction of Llama 3 [15] exemplifies the rapid evolution of MLLMs. This series of models demonstrates native support for multilingualism, coding, reasoning, and tool usage. The most advanced Llama 3 model, boasting 405B parameters and a context window of 128K tokens, exhibits performance comparable to leading models like GPT-4 across a wide range of tasks. Notably, the Llama 3 project extends its capabilities to image, video, and speech processing, showcasing competitive performance with state-of-the-art multimodal models.

Comprehensive evaluations have provided critical insights into the current capabilities and limitations of MLLMs. The MME-RealWorld benchmark by Zhang et al. [16], comprising over 13,000 high-quality images and 29,429 question-answer pairs across 43 subtasks in 5 real-world scenarios, has been particularly illuminating. Evaluations of 29 prominent MLLMs, including GPT-4v, Gemini 1.5 Pro, and Claude 3.5 Sonnet, revealed significant challenges. Even the most advanced models struggled to achieve 60% accuracy, highlighting specific difficulties in processing high-resolution images and comprehending complex real-world scenarios.

Despite these advancements, the specific capabilities of MLLMs in numerical tasks, particularly counting characters in words or objects in visual scenes, remain largely unexplored. This gap presents a unique opportunity to investigate the intersection of visual perception and numerical reasoning in these models. Our research aims to evaluate how MLLMs interpret and quantify visual information, potentially revealing both their strengths and limitations in tasks that bridge multiple modalities. This investigation into counting abilities not only addresses a practical aspect of real-world problem-solving but also offers insights into the cognitive-like processes of MLLMs.

3. Dataset Preparation

To evaluate the counting capabilities of Multimodal Large Language Models (MLLMs), we constructed a custom dataset consisting of both textual and image data, tailored specifically to the objectives of our study. The dataset was designed to thoroughly test the models' ability to count characters in words and objects in images. Below, we provide an overview of the preparation process for the textual and vision parts of the dataset.

Textual Dataset

The textual dataset was derived from the words corpus available in the Natural Language Toolkit (NLTK), a widely used resource for linguistic data. For each word, we calculated its length and analyzed the frequency of each character within it. The character that occurred most frequently was identified, and in cases of ties, one of the frequent characters was selected at random to avoid bias. This process resulted in a mapping between each word, its most frequent character, and its length.

To evaluate MLLMs' counting performance across different word lengths, the words were grouped into three categories based on their length. Words with lengths from one to seven characters were placed in the first group, those between eight and fourteen characters in the second group, and words with fifteen or more characters in the third group. Initially, the dataset contained 50,492 words in the first group, 148,930 words in the second group, and 12,053 words in the third group. Due to the large size and imbalanced distribution of the groups, we randomly sampled 1000 words from each category, resulting in a final, balanced dataset of 3000 words. Each word was associated with its most frequent character and corresponding length, providing a diverse set for evaluation.

To gain a deeper understanding of the dataset’s characteristics, we conducted a statistical analysis of the sampled words. Table 1 and Figure 1 display the distribution of words by the frequency of their most frequent character.

Table 1

Distribution of words by the frequency of the most frequent character

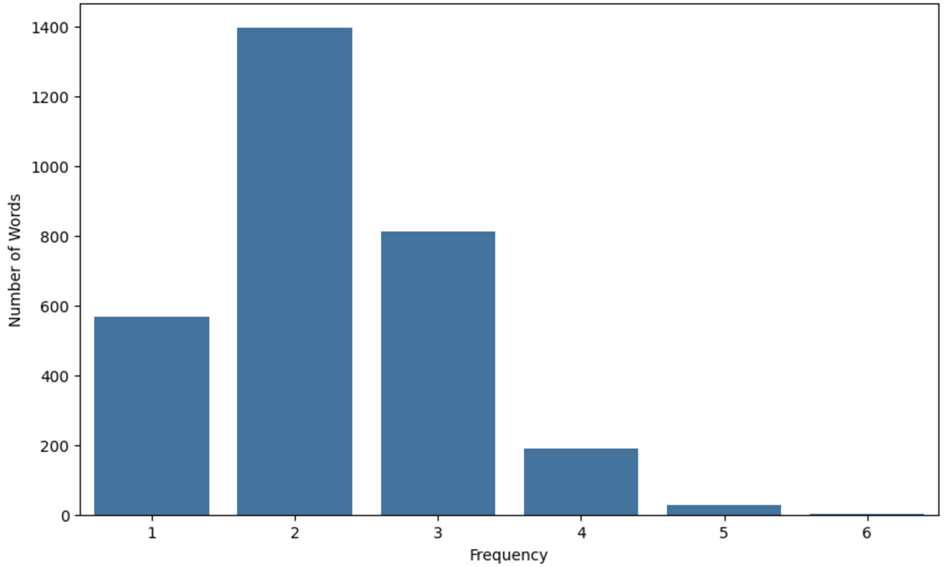
Fig. 1. Distribution of words by the frequency of the most frequent character

Table 2 and Figure 2 display the distribution of words by their most frequent character.

Table 2

Distribution of words by their most frequent character

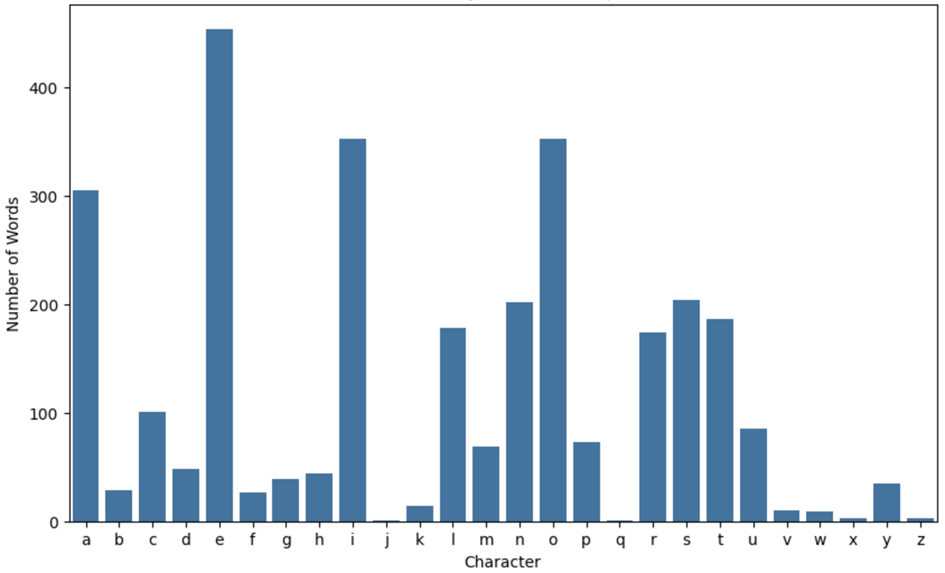
Fig. 2. Distribution of words by their most frequent character

Image Dataset

The evaluation of MLLMs' counting capabilities included a visual dataset in addition to the textual data. For this purpose, we utilized the Pascal Visual Object Classes (VOC)² dataset, a well-known benchmark in computer vision. This dataset comprises various annotated images across multiple categories, making it suitable for assessing object-counting tasks. Figure 3 demonstrates an example from the Pascal VOC dataset.

Fig. 3. Pascal VOC dataset image samples

Similarly to the textual dataset, we conducted a statistical analysis of the sampled images. The distribution of images by the frequency of the most frequent object class is presented in Figure 4. It can be concluded that most of the top objects by frequency appear only once per image.

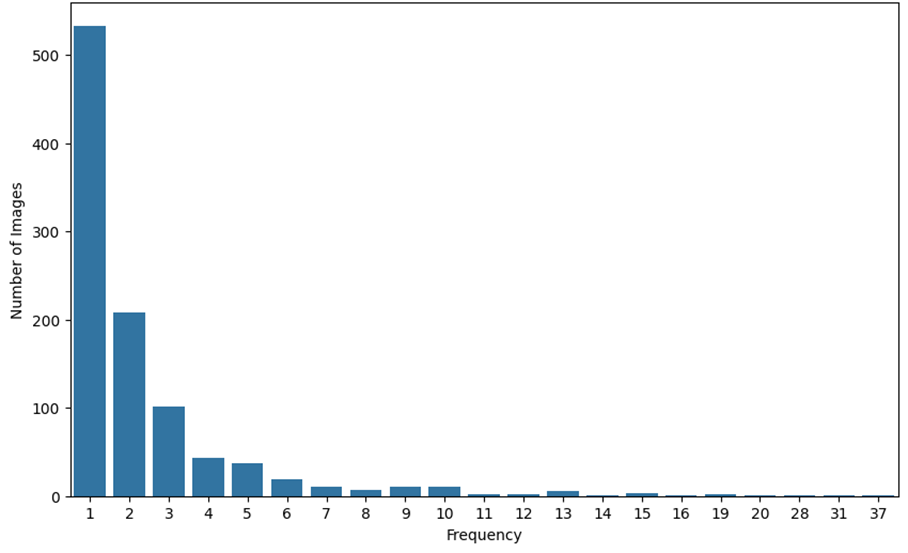
Fig. 4. Distribution of images by the frequency of the most frequent object class

Figure 5 demonstrates the count of images for each object class, where the object class is the most frequent one in the image.

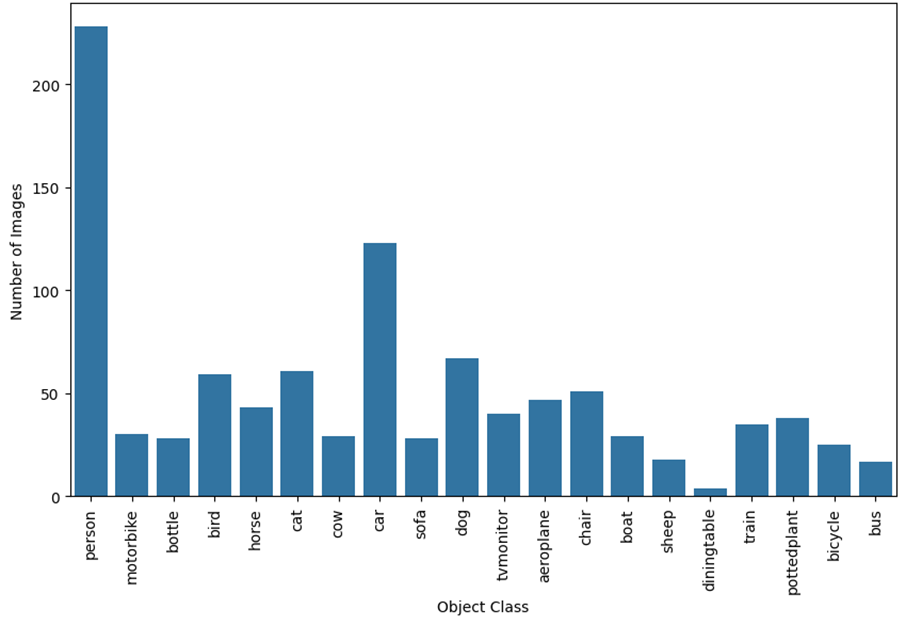
Fig. 5. Distribution of images by the most frequent object class

4. Experimental Setup

4.1. Model Selection

We chose OpenAI's gpt-4o model to evaluate the counting capabilities of multimodal large language models on both textual and visual data. gpt-4o was selected for its state-of-the-art multimodal performance and proven effectiveness across various benchmarks. Although other MLLMs, like Claude from Anthropic, are available, gpt-4o demonstrated the strongest results in almost all of the existing tasks from benchmarks. Since our focus is on assessing MLLMs' counting abilities in general rather than comparing specific models, gpt-4o serves as an ideal choice for this evaluation.

4.2. Prompt Engineering

Our approach to prompt engineering is intentionally straightforward. Instead of crafting complex, layered prompts, we focus on clear, simple instructions to evaluate how well multimodal large language models can handle basic counting tasks. By providing minimal guidance, we aim to assess the models’ effectiveness in performing the tasks without additional contextual help. Below are the prompts used for evaluating the counting capabilities on both textual and visual data.

Textual Prompt

Objective: Count the occurrences of a specific character in a given word.

Prompt: "Count how many times the character '[character]' appears in the word '[word]'. Output only the number."

Visual Prompt

Objective: Count the occurrences of a specific object class in an image.

Prompt: "Count the number of '[object class]' instances in the image. Output only the number."

4.3. Evaluation Metrics

To evaluate the counting capabilities of multimodal large language models (MLLMs) on both textual and visual data, we focus on two key metrics: Accuracy and Mean Absolute Error (MAE). These metrics were chosen for their simplicity and effectiveness in assessing the core objective of our study: to determine the ability of MLLMs to produce precise and reliable counts in straightforward counting tasks.

Accuracy serves as a direct measure of how often the model’s counts are exactly correct. This metric is particularly relevant here, as it provides a clear indication of the model’s success in meeting the counting requirements without deviation. High accuracy reflects the model's ability to consistently provide the correct count in response to simple counting prompts, which is essential in validating its counting proficiency on both text (character counting) and image (object counting) tasks. This metrics is calculated as follows:

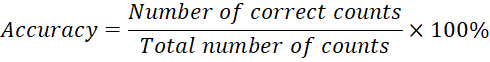(1)

MAE complements accuracy by quantifying the average difference between the model’s predicted counts and the actual counts. While accuracy gives a binary perspective (correct or incorrect), MAE provides a nuanced view of the model's performance when counts are not exact. Lower MAE values indicate that the model’s estimates are generally close to the actual values, even if not always perfectly accurate. Here is the MAE formula:

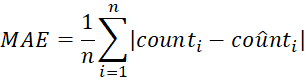(2)

5. Results and Analysis

5.1. Character Counting Results

We performed calculations of metrics both for groups of words with the same lengths and with the same frequency of the most common character. At the same time we have calculated performance metrics independent of groups. Overall metrics are presented in the Table 3.

Table 3

Overall performance metrics

Performance by Word Length Group

Table 3 and Figure 5 present results of counting performance for accuracy and mean average error for groups by word length.

Table 4

Metrics by the word length group

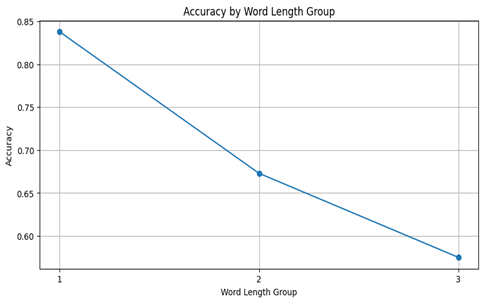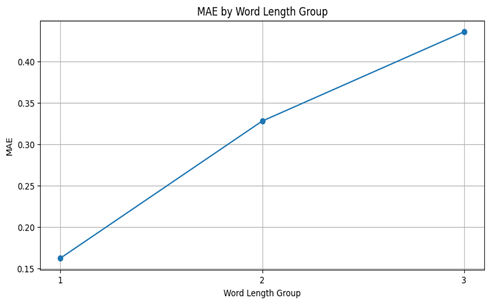Fig. 6. Metrics by the word length group

Performance by Character Frequency

Table 5 and Figure 7 present results of metrics for groups by the top-character frequency.

Table 5

Metrics by the top-character frequency

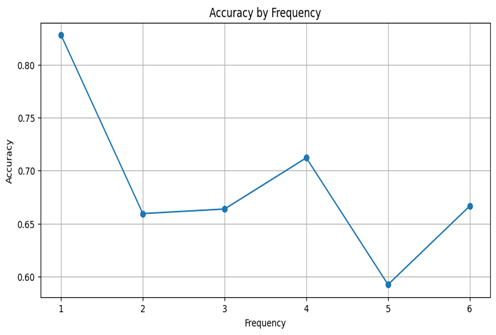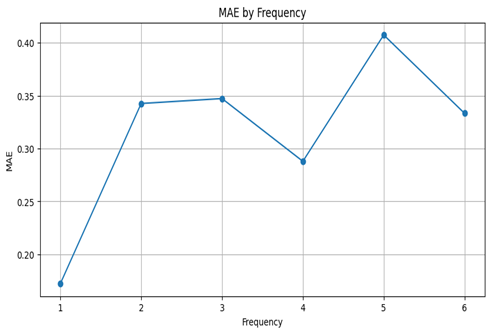Fig. 7. Metrics by the top-character frequency

5.2. Object Counting Results

Similarly to the words, we performed calculations of metrics groups of images with the same most frequent object class and with the same frequency of the most frequent object class. Overall group-independent metrics are in the Table 6.

Table 6

Overall performance metrics

Performance by Object Class

Table 7, Figure 8, and Figure 9 present the metric results for image groups categorized by the most frequent object class. Table 7 focuses exclusively on results for object classes commonly encountered in daily life, while the figures display results for all object classes.

Table 7

Metrics by object class

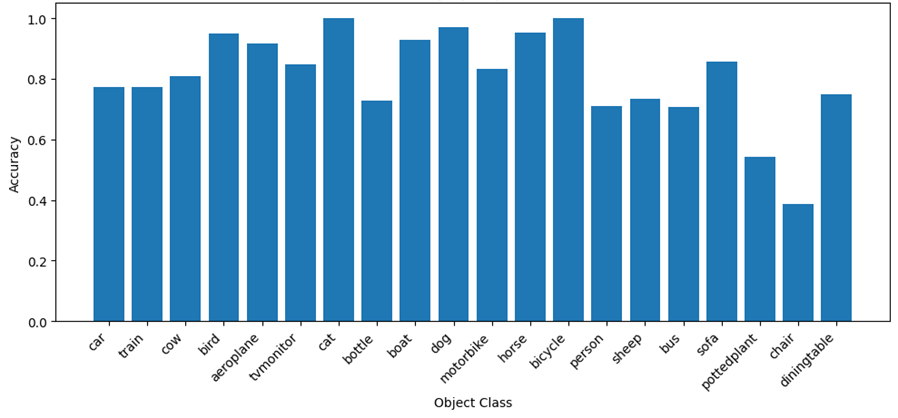
Fig. 8. Accuracy by object class

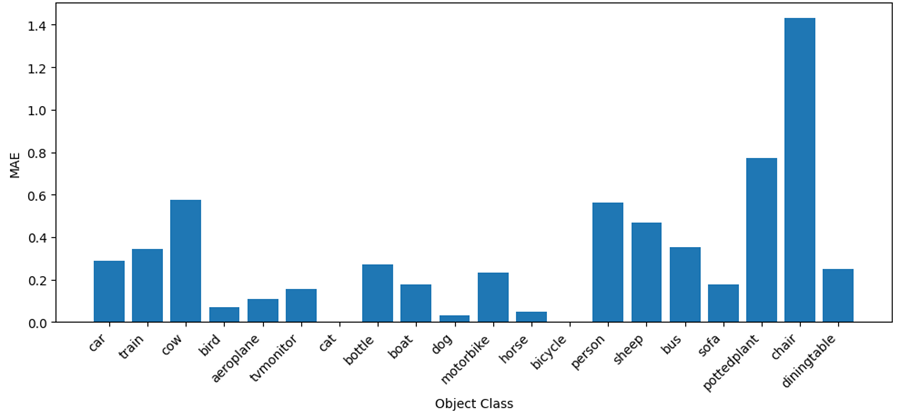
Fig. 9. MAE by object class

Performance by Object Frequency

Table 7 and Figure 10 present the metric results for image groups categorized by the frequency of the most frequent object class.

Table 8

Metrics by object frequency

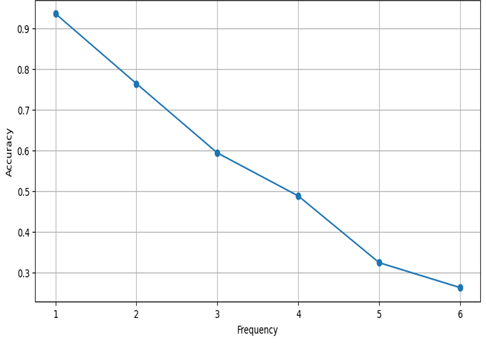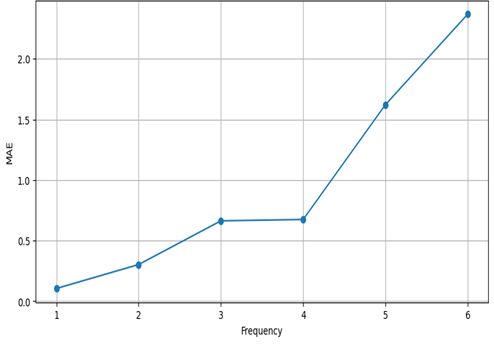Fig. 10. Metrics by object frequency

6. Discussion

Results

Our evaluation highlights that the model achieves moderate accuracy in counting tasks, with 69.5% accuracy and an MAE of 0.31 for text, and 80.3% accuracy with an MAE of 0.34 for images. However, performance varies based on the complexity of the input.

In the textual dataset, the model performs well on shorter words, achieving 83.8% accuracy for single-character words but dropping to 57.5% for three-character words. This decline may be due to the increased complexity of longer words, where characters are harder to isolate, and the model must manage additional contextual information. For character frequency, the model achieves high accuracy at a frequency of 1 (82.7%) but sees diminishing returns as frequency rises. This decline could be due to difficulty tracking multiple identical characters in close proximity, which may lead to errors in distinguishing occurrences.

In the image dataset, the model performs exceptionally well on visually distinct classes, such as cats (100% accuracy) and dogs (97%), likely because these classes have unique, recognizable features that simplify object detection and counting. In contrast, the model struggles with classes like chairs (39% accuracy, MAE of 1.43), where object boundaries may be ambiguous, leading to miscounting. Performance also declines sharply as object frequency increases, with accuracy dropping from 93.6% for single-object images to 26.3% for images containing six objects. This trend likely reflects the model’s difficulty in distinguishing multiple overlapping or clustered instances, which may lead to under- or over-counting in dense settings.

Limitations of Current Multimodal LLMs in Counting Tasks

While the model demonstrates competence in simpler counting tasks, several limitations emerge in more complex scenarios. Performance declines with increased input complexity–longer words or dense object arrangements–suggest that current multimodal LLMs struggle to manage intricate visual and textual patterns where objects or characters require fine-grained distinction. These results imply that while multimodal LLMs are promising for straightforward counting, they require refinement to handle more nuanced counting tasks, particularly in high-density or context-rich environments.

7. Conclusion

This study examined the counting capabilities of a multimodal large language model (MLLM) across textual and visual data, using simple prompts to assess its ability to accurately count characters in words and objects in images. The model showed moderate success, achieving 69.5% accuracy in text-based counting tasks and 80.3% in image-based tasks. However, performance varied significantly with input complexity: accuracy declined as word length increased or as object counts and density grew in images. These results suggest that while the model can handle basic counting tasks, it faces limitations when confronted with intricate structures, such as longer words or densely populated images.

The findings highlight both the promise and the current limitations of MLLMs in counting tasks, with strengths in clear, simple contexts but challenges in complex, overlapping, or high-density scenarios. This points to an opportunity for future work to refine MLLMs to improve their handling of more demanding counting tasks, enhancing their utility in applications requiring precise object or character quantification.