The STEM Project M-MOTR: an economic-mathematical model for optimizing transport routes in logistics and supply chain management

In 2022, research on the promising The STEM Project M-MOTR was launched at the Academy of Industrial Technologies in St. Petersburg. And in the present year, 2025, we would like to share the first results and successes of our research.

In an era marked by the rapid expansion of global trade, the logistics and supply chain management sector faces unprecedented challenges in ensuring the efficient movement of goods. As consumer demands evolve and market dynamics fluctuate, the optimization of transport routes has emerged as a critical element in enhancing operational efficiency and maintaining competitive advantage. The STEM Project M-MOTR addresses these challenges by presenting a novel economic-mathematical model specifically designed to optimize transport routes within complex logistics frameworks.

M-MOTR stands out as a pioneering initiative that leverages advanced mathematical concepts and data-driven approaches to refine logistics strategies. Its primary objective is not only to reduce transportation costs and minimize delivery times but also to adapt dynamically to a myriad of changing variables including traffic patterns, fluctuating fuel costs, and the availability of vehicles. By integrating real-world economic factors into a robust algorithm, M-MOTR serves as a comprehensive tool tailored to address the intricacies of modern supply chain networks.

Key achievements of the M-MOTR project include the successful development and implementation of an algorithm that shows remarkable adaptability to the ever-changing logistics landscape. Extensive testing and validation across diverse logistical contexts have demonstrated the model's capacity to significantly enhance route optimization outcomes compared to traditional methodologies. Such empirical findings highlight the transformative potential of mathematical modeling in reshaping logistics strategies, paving the way for more efficient and sustainable supply chain practices.

Foreign experience shows that a qualitative "leap" in the field of transport is transportation that meets modern requirements and high international standards it is possible to achieve this only through the use of new technologies for ensuring logistics processes, in particular, by expanding the development of logistics thinking and the principles of logistics [1, p. 122-127].

In this regard, it is interesting to compare our findings with those of colleagues from the research group of the Voronezh State University of Engineering Technologies.

The mathematical model of the transport problem looks like this:

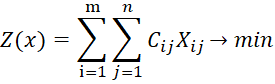, (1)

The mathematical description of the complete inventory of transport service providers is a system of equalities:

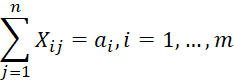, (2)

The math. description of customer satisfaction is expressed by the ratio:

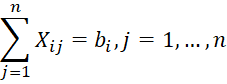, (3)

The condition of non-negativity of all variables of the problem has the form:

, (4)

Next, you need to add a mathematical description of the general inventory of suppliers and consumers, indicating the types of tasks. If equality occurs, then we have a task type with the correct balance, and the model is closed, if it is not respected, then the model looks like:

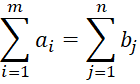, (5)

At the end of the reflections, the stages of solving transport problems using the potential method are given [2, p. 226-232].

Colleagues from Belarusian State University of Transport, Gomel, Republic of Belarus they offer returning to the need for a qualitative selection of factors for factor analysis in the design and development of passenger hubs, it is important to note that in order to provide passengers with a seamless transportation experience, different nations have different selections of criteria that influence the utilization of passenger transportation hubs [3, p. 16-21].

Other colleagues from the St. Petersburg Federal Research Center of the Russian Academy of Sciences believe that figures 4 and 5 show statistics on the number of cases in which simple routes have been improved by complex ones.

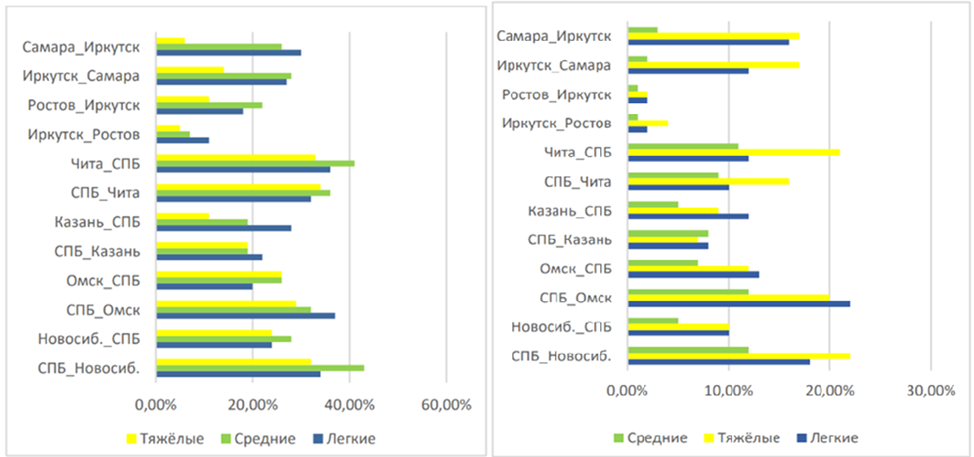
Fig. Statistics of a simple route cost increase by complex ones in selected directions and statistics of significant improvements in a simple route cost by complex ones in selected directions

The cost of transportation between Any pair of cities was calculated for three categories of cargo, with three cargoes in each category. As a result, in more than 40% of cases, for goods classified as "medium", that is, from 50 to 500 kg, a composite route was found that turned out to be cheaper than a direct route [4, p. 309-319].

It is also necessary to improve transport and logistics infrastructure, taking into account the provision of a wide range of services in any direction. Here it is necessary to consider the competitiveness of tariffs and to create conditions for further improvement of corridors for transit cargo flows on a permanent basis. In transport logistic terms of cargo passage and their directions, cost and systematic use of transport corridors should be clearly defined [5, p. 88-96].

Some assistants of the Azerbaijan State University Oil and Industry, Baku, Azerbaijan believe that obstacles to intermodal transportation. Since a significant proportion of transshipment costs is a key factor preventing the wider use of intermodal transport over shorter distances, one of the important aspects of intermodal efficiency is nodal points. Facilities at the nodes should be standardized to provide efficient services, accessibility to these nodes should be developed or improved, and transportation the systems must be integrated [6, p. 108-112].

Real-world applications of mathematical models in logistics are typically scrutinized through empirical evidence or case studies, which illustrate how theoretical approaches can be applied to solve practical challenges. Without such examples, the research risks being perceived as abstract or devoid of operational significance, limiting its contribution to the field of transport logistics.

Mathematical modeling in the logistics sector represents a powerful approach to solving complex problems while optimizing operations and enhancing efficiency. Below is a comprehensive overview of mathematical modeling's objectives, methodologies, and applications in the logistics sector, particularly in relation to projects such as M-MOTR.

Model Types various types of mathematical models are utilized, including.

Linear Programming (LP): Used for problems where relationships are linear, such as minimizing costs subject to constraints. Linear Programming is a technique used for optimization where the objective function and constraints are all linear relationships.

An LP problem can be expressed as follows:

, (6)

Subject to constraints:

Optimizing the shipment of goods from multiple suppliers to multiple consumers. Allocating hours among employees to minimize costs while meeting labor laws and customer demand.

Mixed-Integer Programming (MIP): Combines integer and continuous variables to address more complex logistics scenarios. Mixed-Integer Programming extends linear programming by allowing some decision variables to be constrained to take on integer values.

A MIP problem can be specified as follows:

, (8)

Subject to constraints:

Deciding where to locate warehouses or distribution centers while minimizing operational costs. Determining optimal routes for delivery vehicles while taking into account capacity constraints.

Dynamic Programming: Useful for problems that involve sequential decision-making. Dynamic Programming is an algorithmic technique for solving complex problems by breaking them down into simpler subproblems. It is particularly effective for problems where decisions are made in stages and where optimal solutions can be constructed from optimal solutions of subproblems.

Stochastic Models: These incorporate randomness and uncertainty, reflecting real-world variability. Stochastic models incorporate randomness and uncertainty into the modeling process, reflecting the inherent variability of real-world logistics scenarios. These models are particularly useful for predicting outcomes when certain parameters (e.g., demand, lead times) are not predictable.

Simulation Models: Allow for the testing of scenarios through computational models to predict outcomes based on different parameter settings. Simulation models replicate the operations of a logistics system over time, allowing for "what-if" analyses and scenario testing. These models can accommodate complexity and variability in operations that might be difficult to capture with analytical models.

Mathematical models are widely used to optimize transportation routes, taking into consideration various factors such as time, cost, distances, and capacities. Projects like M-MOTR demonstrate how dynamic algorithms can adjust routes based on real-time conditions. Models help determine optimal order quantities, reorder points, and inventory levels to minimize holding costs while ensuring that customer demand is met promptly. Mathematical models assist in determining the best locations for warehouses and designing their layouts to minimize transportation costs and maximize service coverage. The advancement of technologies, such as IoT, big data analytics, and AI allows for the incorporation of real-time data into mathematical models, improving their accuracy and effectiveness.

The M-MOTR project presents a comprehensive framework for optimizing transport routes, and its successful preliminary testing in large logistics companies in state indicates promising potential across multiple domains. The expected results highlight improvements in efficiency, cost savings, and sustainability, positioning participating companies to thrive in an increasingly competitive and dynamic logistics environment. As organizations continue to embrace data-driven and algorithmic approaches, the long-term impact of M-MOTR could significantly transform logistics strategies and practices.

The M-MOTOR project, which focuses on improving transport logistics performance, uses a special algorithm designed to optimize processes based on existing solutions. This algorithm combines elements of artificial intelligence, machine learning, graph theory and optimization mathematics, which makes it possible to manage the flow of goods much more efficiently and reduce costs.

Mathematical modeling is a cornerstone of effective logistics and supply chain management. By utilizing various methodologies to optimize routes, minimize costs, and enhance service levels, organizations can navigate the complexities of modern supply chains more effectively. The M-MOTR project exemplifies how advanced mathematical models can address real-world challenges, driving operational efficiency and sustainable practices in logistics.