Прежде чем приступить к анализу теорий излучения и поглощения на основе уравнений в классической электродинамике, мы вынуждены отметить и повторить, что многие парадоксы, допущенные физиками, связаны с упрощениями, сделанными в математике с исключением логики Мироздания на основе замкнутой системы из двух глобальных противоположностей [2, с. 5-37]. Само наличие противоположностей в Мироздании связано с логикой исключения парадоксов. Действительно, представить наличие объекта в однородной среде невозможно, так как нет признаков отличий. Замкнутость противоположностей друг на друга с взаимодействием через действие и противодействие, и обмен, связана с тем, что иначе они друг для друга не существуют. Соответственно мы должны остановиться на правилах взаимодействия противоположностей, так как математика с её допущениями даёт парадоксы в физике. Так, в математике вычитание приводит к обнулению, в физике это даёт преобразование в иной вид, например аннигиляция электрона и позитрона связана с превращением в фотоны, а столкновение фотона с препятствием даёт электрон и позитрон. То есть, основной вопрос, который не смогла решить современная наука, касался принципа взаимодействия, что связано с излучением и поглощением, что, собственно, мы и рассмотрим в этой статье. Именно поэтому Бор решил отказаться от идеи классического закона электродинамики, связанного с излучением на дискретных орбитах, при вращении электрона вокруг протона, так как не знал способа возвращения (обратного поглощения) энергии. Однако только через обмен чем-то между объектами можно объяснить их взаимодействие, иначе они независимы друг от друга, так как полностью замкнуты сами на себя. Для разрешения парадокса следовал вопрос: «Что должно излучаться и поглощаться, и какая логика должна при этом быть?» Проблема усугублялась тем, что наряду с отталкиванием объектов, связанным с передачей кинетической энергии, есть ещё и притяжение объектов, что передачей кинетической энергии при однородности фотонов не объяснишь. И здесь логика основывается на том, что обмен связан с движением, а значит и кинетической энергией, и именно поэтому энтропия по закону Больцмана возрастает до бесконечности [3, с. 333]. При этом физики из этого сделали вывод о бесконечном расширении, что связано с силами отталкивания и отсюда была предложена космологическая инфляционная теория [4]. Как решить эту проблему без парадокса однородности фотонов, связанного с отталкиванием? Собственно выход уже был связан с тем, что на практике наблюдалось притяжение противоположно заряженных частиц и отталкивание однородно заряженных частиц и это определяло наличие у объектов обмена разных свойств. Однако тут же возникал вопрос: «С чем связано такое различие и деление, и каким образом обеспечивается это самое притяжение и отталкивание?» Не найдя объективного решения физики, придумали виртуальные фотоны, которые извлекаются и исчезают в тоже выдуманном электромагнитном вакууме [5, с. 147-338]. Именно через их воздействие они решили объяснять как отталкивание, так и притяжение. Но вот тут сразу возникают вопросы. Виртуальные фотоны из электромагнитного вакуума, которые становятся реальными, должны обладать кинетической энергией, а значит иметь направление движения. В противном случае нет возможности их обнаружить. Тогда первый вопрос: «Каким образом в электромагнитном вакууме формируются виртуальные фотоны с нужным направлением движения, что позволяет в одном случае при одноимённых зарядах обеспечивать отталкивание, а при разноимённых зарядах – притяжение?» Иными словами, виртуальные фотоны должны различать заряды, но при однородности виртуальных фотонов это невозможно в силу того, что нет признака отличия для оказания разного действия. Второй вопрос касается закона сохранения количества (энергии). Действительно, если предположить электромагнитный вакуум как бесконечный источник энергии для превращения виртуальных фотонов в реальные фотоны, то каким образом происходит это преобразование, и из чего? Если виртуальные фотоны возникают из нуля, то в этом случае это аналогично чудесам без необходимости наличия законов физики с условием закона сохранения количества и здесь нет противодействия на действие, что равносильно существованию Бога. Ситуацию не спасает и соотношение неопределённостей Гейзенберга, так как воздействие виртуальных фотонов, существующее даже короткое время, даёт реальный эффект в виде энергии, но, тогда как уже реальная энергия вдруг исчезает в вакууме и по какому закону? А если электромагнитный вакуум не ноль, то должно быть его реальное описание как объекта через свойства присущие всем объектам Мироздания, так как в противном случае получается его независимость, и нет взаимодействия на основе законов физики. То есть, повторим, что парадокс касается того, что виртуальные фотоны должны передавать кинетическую энергию заряженным объектам для притяжения и отталкивания. Одновременно при потере этой энергии должно происходить излучение по законам электродинамики уже реальных фотонов, а они исчезнуть в электромагнитном вакууме не могут, нет механизма превращения в ноль. Иными словами, выдуманные виртуальные фотоны и электромагнитный вакуум, как некая среда без представления через физические величины для взаимодействия в уравнениях физики, дают неразрешимые парадоксы.
Кроме того, чтобы электромагнитный вакуум создавал необходимые виртуальные фотоны с нужным направлением, должен быть признак, который формируется от воздействия заряженных объектов на электромагнитный вакуум, но тогда вопрос: «За счет, каких объектов, и каким образом формируется это воздействие?» Иными словами, должно быть взаимодействие заряженных объектов с электромагнитным вакуумом, а как мы показали выше, это может происходить только через обмен чем-то. Причём эти объекты для обмена, формирующие признак различия, должны быть разные в соответствии с наименованием заряда, иначе для электромагнитного вакуума нет разницы в формировании виртуальных фотонов по направлению. Так как объекты с разноимёнными зарядами сохраняются во времени, то это означает, что помимо излучения при взаимодействии должно быть и поглощение этого нечто. Однако, если ориентироваться на излучение и поглощение фотонов (виртуальных или реальных), то есть варианта, когда излучается то, что поглощается, то получить различие во взаимодействии относительно разноимённых зарядов невозможно, так как нет признака и различия самих зарядов по взаимодействию. На основании сказанного следует вывод, что различие между противоположными зарядами объектов основано на том, что объекты с противоположными зарядами имеют излучение объектов, отличающихся друг от друга. Но как мы отметили выше, объекты сохраняются во времени без распада, а это означает, что должно быть восполнение объектов излучения. Если объекты противоположных зарядов излучают тоже что и поглощают, то мы имеем вариант отсутствия необходимости взаимодействия противоположных зарядов, так как между ними нет обмена. Поэтому остаётся только вариант, при котором, для взаимодействия и обмена между противоположно заряженными объектами, то, что излучается объектом одной полярности (вида), поглощается объектом другой полярности, и наоборот. Понятно, что поглощение одних объектов и излучение других объектов, означало бы перерождение объектов, чего на практике не наблюдается. Поэтому остаётся вариант, когда сами объекты являются преобразователями из одного вида в другой вид в обратном направлении. Это означает, что внешний обмен с взаимодействием противоположно заряженных объектов, с различием объектов взаимодействия, компенсируется обратным внутренним противоположным обменом и взаимодействием в объекте. Собственно, обнаружить объект, который не вносит преобразования невозможно. Это означает однородность и исключает наличие противоположностей. Отметим, что даже смена направления движения объекта связана с преобразованиями, так как при этом передаются (излучаются) одни компоненты, а поглощаются другие компоненты, так как иначе изменения направления движения не получить (имеем так называемое инерционное движение объекта). При этом мы имеем различие так называемых противоположно заряженных объектов по противоположным друг другу схемам преобразования по поглощению и излучению. Из сказанного следует, что помимо фотонов, которые поглощаются и излучаются противоположными объектами мироздания, должны быть объекты, отличие которых обеспечивает представление физиков о противоположных зарядах. Соответственно возникает вопрос: «Что собой должны представлять эти объекты для взаимодействия и обмена?» При этом, если исходить из схемы формирования объектов от простого к сложному (иное даёт разрыв, а значит утверждает чудеса), то должен быть переход от самых элементарных объектов к более сложным за счёт взаимодействия. Кроме того, здесь возникает вопрос и о взаимодействии этих объектов с окружающей средой. То есть должна быть альтернатива электромагнитному вакууму в версии физиков, так как взаимодействие объектов осуществляется через среду распространения, и именно её взаимодействие через обмен с объектом определяет его характеристики по сохранении во времени и движению. Собственно влияние среды на объекты отражено и через искривление движения электромагнитных волн в пространстве с наличием принципа Гюйгенса-Френеля, так как в противном случае было бы только прямолинейное движение без огибания волной препятствия. При решении указанных вопросов в объектах взаимодействия мы неизменно приходим к понятию скорости обмена (поглощения, излучения).
В [1, с. 7-38] мы показали и обосновали не только необходимость ограничения скорости света (обмена), но и наличие минимального объекта в Мироздании в соответствии с формулой:
![]() , (1)
, (1)
То есть мы получили: произведение скорости света (с) на величину постоянной Планка (h) определяет значение константы нашего мироздания по взаимодействию.
Понятно, что при скорости обмена равной нулю взаимодействия нет, и объекты друг для друга не существуют. При скорости обмена равной бесконечности законы физики не существуют, так как изменений при законе сохранения количества зафиксировать невозможно. Действие тут же компенсируется противодействием, а это исключает изменения, а значит и законы физики. Отсюда остаётся вариант, когда скорость обмена между глобальными противоположностями определяется некоторым количественным значением. В силу того, что глобальные противоположности в Мироздании замкнуты друг на друга за счёт взаимодействия и отсутствия исчезновения одной из них, то Мироздание является константой, то есть не является закономерностью и как в константу в неё входят все закономерности. А отсюда следует, что скорость обмена между глобальными противоположностями также является константой. Собственно, с практической точки зрения представление скорости обмена как константы было определено и Эйнштейном в его специальной теории относительности (СТО) в виде скорости света. Однако непонимание физиками самой логики наличия скорости света (скорости обмена) как константы привело к тому, что они выдвинули гипотезу о существовании тахионов, движущихся со скоростью большей, чем скорость света [6, с. 216-217]. Собственно эта ошибка была связана с отсутствием понимания равноправия в системах наблюдения от противоположностей и исходила из наличия волн Луи де Бройля, которые по предположению физиков должны были двигаться со скоростью больше, чем скорость света (аналог фазовой скорости в волноводе, но без наличия металлической оболочки отражения). Учитывая замкнутость Мироздания, скорость света (обмена) должна быть такой, что во взаимодействии должны участвовать все объекты Мироздания, иначе их нет в нашем Мироздании. Понятно, что в этом случае количество объектов в Мироздании должно быть ограничено. То есть, определить скорость обмена для бесконечно малого объекта не представляется возможным. Отсюда следует известный парадокс математики, при котором быстроногий Ахиллес, при отображении движения через приращения дискретных величин практически до нуля, никогда не догонит неторопливую черепаху, если в начале движения черепаха находится впереди Ахиллеса.
Так, задавшись величиной минимального объекта Nнач, и определив его скорость передачи (обмена, изменения) как S, мы при наличии бесконечно малых объектов другой величины всегда можем представить этот объект как Nнач=kn, где n ‒ это еще меньший по величине объект (собственно физики это и сделали через кварки и глюоны). Соответственно, скорость передачи s для отдельного объекта n должна быть выше в k раз, чем значение S, чтобы обеспечить взаимодействие со всеми объектами, так как в противном случае получаются объекты без взаимодействия, а значит, их и нет в мироздании. В этом случае при стремлении шага величины дискретизации (h) к нулю нет и предела скорости обмена (c), которая вырастает до бесконечности. При этом мы напоминаем, что любые изменения у нас связаны с переходом в противоположность, поэтому вариант с движением в одной противоположности, например движение поезда (чисто корпускулярное движение), здесь не подходит, так как в этом случае рассматривается вариант без взаимодействия с противоположностью, то есть отрицается необходимость самих противоположностей.
Здесь мы имеем следующую логическую цепочку. Замкнутость мироздания определяет постоянство скорости обмена при взаимодействии, что приводит и к наличию минимального шага дискретизации. Так как взаимодействие возможно только в случае обмена, то исключить независимость отдельных элементов можно только тогда, когда общий количественный обмен, который и характеризует энергию взаимодействия, определяется по формуле произведения скорости света и постоянной Планка!
Понятно, что данные утверждения должны соответствовать формулам для физических явлений, поэтому отметим, что необходимость связи скорости света с постоянной Планка уже была введена до нас в физике как постоянная тонкой структуры [7, с. 341]:
![]() , (2)
, (2)
Разница лишь в нормировке связанная с системой измерения. Её можно пересчитать, если учесть, что заряд по теории Дирака [8, с. 349] имеет значение равное плюс или минус единице (![]() ), так как величины заряда нет в формуле энергии Эйнштейна, и его роль сводится к представлению операции излучения или поглощения, то есть не количества, а действия через знак (
), так как величины заряда нет в формуле энергии Эйнштейна, и его роль сводится к представлению операции излучения или поглощения, то есть не количества, а действия через знак (![]() ) – закономерности. Отсутствие значения заряда в формуле энергии Эйнштейна означает и отсутствие у заряда силового воздействия, так как нет энергии для этого. Ещё раз отметим, что придумать иной принцип взаимодействия помимо обмена − невозможно, а обмен обязательно характеризуется скоростью и величиной шага дискретизации. Собственно, и физики не смогли обойтись без взаимодействия, но придумали для этого виртуальные фотоны и гравитоны, которые имеют воздействие через телепортацию (так как нет математического аппарата и физических законов связи). Помимо этого, надо ещё раз отметить, что произведение скорости обмена (света) на шаг дискретизации (постоянная Планка) имеет значение, равное единице, в противном случае либо скорость обмена, либо шаг дискретизации имеют иную величину. С учётом нашей теории мы имеем
) – закономерности. Отсутствие значения заряда в формуле энергии Эйнштейна означает и отсутствие у заряда силового воздействия, так как нет энергии для этого. Ещё раз отметим, что придумать иной принцип взаимодействия помимо обмена − невозможно, а обмен обязательно характеризуется скоростью и величиной шага дискретизации. Собственно, и физики не смогли обойтись без взаимодействия, но придумали для этого виртуальные фотоны и гравитоны, которые имеют воздействие через телепортацию (так как нет математического аппарата и физических законов связи). Помимо этого, надо ещё раз отметить, что произведение скорости обмена (света) на шаг дискретизации (постоянная Планка) имеет значение, равное единице, в противном случае либо скорость обмена, либо шаг дискретизации имеют иную величину. С учётом нашей теории мы имеем ![]() . С физической точки зрения это означает, что объект с радиусом r в одной противоположности формируется за счёт движения по окружности величиной
. С физической точки зрения это означает, что объект с радиусом r в одной противоположности формируется за счёт движения по окружности величиной ![]() в другой противоположности. При этом, как будет показано ниже, длина в одной противоположности не является длиной в другой противоположности и здесь есть также обратно-пропорциональная связь. То есть постоянная тонкой структуры в интерпретации изменений за счёт систем измерения выступает как единица пересчёта между противоположностями. Надо отметить, что взаимодействие через обмен происходит именно при движении по окружности, так как только в этом случае происходит изменение составляющих. Радиус в данном случае выступает как константа и поэтому характеризовать динамику взаимодействия не может. Именно поэтому уравнение гармонического осциллятора выбрано в физике для описания взаимодействия объектов. Одновременно из формулы (1) следует необходимость и ограничения числа объектов в Мироздании по формуле:
в другой противоположности. При этом, как будет показано ниже, длина в одной противоположности не является длиной в другой противоположности и здесь есть также обратно-пропорциональная связь. То есть постоянная тонкой структуры в интерпретации изменений за счёт систем измерения выступает как единица пересчёта между противоположностями. Надо отметить, что взаимодействие через обмен происходит именно при движении по окружности, так как только в этом случае происходит изменение составляющих. Радиус в данном случае выступает как константа и поэтому характеризовать динамику взаимодействия не может. Именно поэтому уравнение гармонического осциллятора выбрано в физике для описания взаимодействия объектов. Одновременно из формулы (1) следует необходимость и ограничения числа объектов в Мироздании по формуле:
![]() , (3)
, (3)
Фактически это означает, что ни один объект не может войти или выйти из замкнутой на две глобальные противоположности системы Мироздания (вечное существование нашего «я» как объекта Мироздания). Таким образом, мы видим, что предположение Эйнштейна о постоянстве скорости света вытекает не из относительности точки наблюдения с соблюдением одинаковых законов физики в разных системах отсчёта, а из логики наличия замкнутой системы Мироздания на две глобальные противоположности. Именно подход с точки зрения относительности ставил учёных в тупик, когда они рассматривали движение двух объектов, движущихся навстречу друг другу из третьей точки наблюдения, и у них выходило, что при относительности объекты навстречу друг другу должны были двигаться со скоростью больше, чем скорость света. Соответственно второй парадокс в СТО Эйнштейна касался того, почему при возврате движущихся часов в систему с часами в состоянии покоя замедление времени было у часов, которые испытывали ускорение. Разрешение этого парадокса связано с тем, что здесь нет принципа относительности в плане неизменности длины и времени в разных противоположных системах наблюдения. Однако законы физики остаются одинаковыми, в силу условия закона сохранения количества при обмене и замкнутости Мироздания, что определяет симметрию и инвариантность. После ускорения на основании полученной энергии произошло пространственно-временное искривление, где длина и время имеют другое количественное измерение по отношению к системе наблюдения в покое, с соблюдением общей инвариантной формы, что и определило разницу во времени. Эйнштейн исходил из неизменности физических законов в разных системах наблюдения в СТО, но не учитывал, что сами противоположности длины и времени по отношению друг к другу в других системах наблюдения имеют иное представление, что, собственно, и породило ОТО. И именно разница представления длины и времени в зависимости от системы наблюдения определяет и разницу в физической интерпретации объектов в этих системах наблюдения, так как отсюда и формируется представление о значении кинетической и потенциальной энергии. Соответственно переход кинетической энергии в потенциальную энергию, и наоборот, меняет и само отображение объекта, что означает его представление в зависимости от системы наблюдения. Однако эту логику не смогли понять физики и А. Эйнштейн, хотя именно такой подход позволяет интерпретировать движущийся электрон вокруг протона в первой системе наблюдения, как неподвижный антипротон в противоположной второй системе наблюдения, связанной с первой системой через скорость света. Соответственно протон из первой системы наблюдения будет выглядеть уже позитроном, движущимся вокруг антипротона во второй системе наблюдения. Непонимание необходимости такой логики привело к представлению протона и нейтрона через кварки и глюоны (рис. 1).
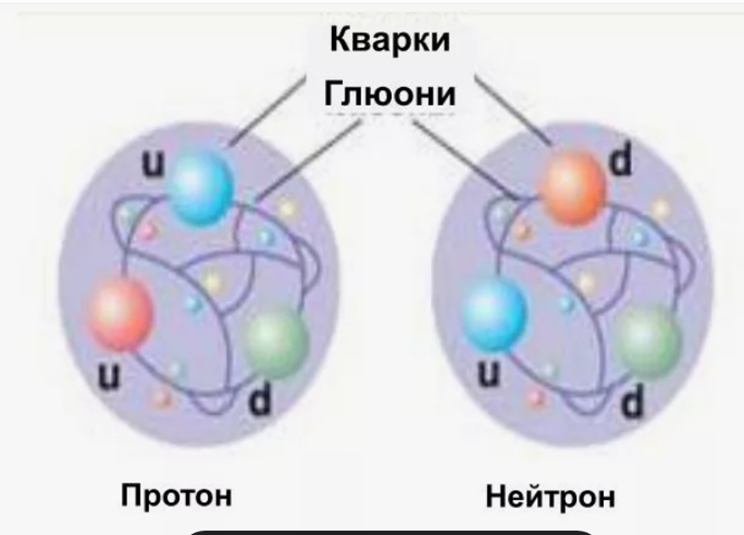
Рис. 1. Представление о взаимодействии протона и нейтрона на основе кварков и глюонов
Понятно, что это явно смахивает на формирование желаемых образов, как икон в религии.
Следует отметить, что сами преобразования Лоренца по СТО также соответствовали замкнутой системе на две глобальные противоположности, где сложение в одной противоположности означало вычитание в другой противоположности. Это мы показали в [1, с. 7-38] сделав следующие преобразования СТО Эйнштейна в замкнутом виде:
(4) |
Если рассматривать взаимосвязь глобальных противоположностей через скорость света (обмена), то vx=c. Отсюда имеем:
![]() , (5)
, (5)
На основании этого была обоснована общая формула Мироздания:
(6) |
Здесь ![]() , в этом случае аргументы имеют равенство по количеству. При этом мы имеем различие противоположностей на основе атрибута в виде мнимой единицы, что даёт смену закономерностей в зависимости от системы наблюдения. Собственно формула (6) определяет известный закон философии перехода количественного значения объектов в новое качество, связанное с закономерностями. Действительно, нельзя получить количественное равенство по (6) при вычитании слева от знака равенства и сложении в правой части равенства, если нет изменения качества за счёт закономерностей. Более подробно на основе элементарной логики вывод данной формулы общего закона Мироздания мы рассмотрели в [2, с. 5-37]. Здесь мы только подметили, что такой же вывод получается и на основе СТО Эйнштейна на основании формулы (5). Из формулы (6) следует, что между глобальными противоположностями нет количественного отличия, а различие касается только представления процессов в зависимости от системы наблюдения, где процессы, которые связаны со сложением в одной системе наблюдения и от первой противоположности, выглядят вычитанием от системы наблюдения от второй глобальной противоположности. При этом происходит смена закономерностей за счёт атрибута принадлежности в виде мнимой единицы, что, собственно, определяет смену свойств и отображения. И такое различие в физике получило название корпускулярно-волнового дуализма для объектов. Действительно, объект должен иметь как составляющую от одной противоположности, так и составляющую от другой противоположности, так как в противном случае он будет замкнут и однороден в одной противоположности без взаимодействия. Но если он не участвует во взаимодействии через обмен, то обнаружить его невозможно. Именно такую ошибку совершили физики, когда вдруг «открыли» наличие бозона Хиггса на Большом Андроном Коллайдере, так как бозон Хиггса не может иметь электромагнитных волновых свойств в силу его полной нейтральности. Однако на практике бозон Хиггса распадается именно на фотоны. Иными словами, эксперимент явно не совпадает с теорией, предложенной физиками. Понятно, что на основе подчинения общей формуле Мироздания должны строиться и законы физики. Собственно, это мы показали в [1, с. 7-38], когда показали переход от общей формулы мироздания к формуле энергии Эйнштейна на основе уравнения гармонического осциллятора в виде [9, с. 58-59]:
, в этом случае аргументы имеют равенство по количеству. При этом мы имеем различие противоположностей на основе атрибута в виде мнимой единицы, что даёт смену закономерностей в зависимости от системы наблюдения. Собственно формула (6) определяет известный закон философии перехода количественного значения объектов в новое качество, связанное с закономерностями. Действительно, нельзя получить количественное равенство по (6) при вычитании слева от знака равенства и сложении в правой части равенства, если нет изменения качества за счёт закономерностей. Более подробно на основе элементарной логики вывод данной формулы общего закона Мироздания мы рассмотрели в [2, с. 5-37]. Здесь мы только подметили, что такой же вывод получается и на основе СТО Эйнштейна на основании формулы (5). Из формулы (6) следует, что между глобальными противоположностями нет количественного отличия, а различие касается только представления процессов в зависимости от системы наблюдения, где процессы, которые связаны со сложением в одной системе наблюдения и от первой противоположности, выглядят вычитанием от системы наблюдения от второй глобальной противоположности. При этом происходит смена закономерностей за счёт атрибута принадлежности в виде мнимой единицы, что, собственно, определяет смену свойств и отображения. И такое различие в физике получило название корпускулярно-волнового дуализма для объектов. Действительно, объект должен иметь как составляющую от одной противоположности, так и составляющую от другой противоположности, так как в противном случае он будет замкнут и однороден в одной противоположности без взаимодействия. Но если он не участвует во взаимодействии через обмен, то обнаружить его невозможно. Именно такую ошибку совершили физики, когда вдруг «открыли» наличие бозона Хиггса на Большом Андроном Коллайдере, так как бозон Хиггса не может иметь электромагнитных волновых свойств в силу его полной нейтральности. Однако на практике бозон Хиггса распадается именно на фотоны. Иными словами, эксперимент явно не совпадает с теорией, предложенной физиками. Понятно, что на основе подчинения общей формуле Мироздания должны строиться и законы физики. Собственно, это мы показали в [1, с. 7-38], когда показали переход от общей формулы мироздания к формуле энергии Эйнштейна на основе уравнения гармонического осциллятора в виде [9, с. 58-59]:
![]() , (7)
, (7)
Из уравнения гармонического осциллятора (8) Бор также получил формулы вида:
(8) |
Фактически Бор связал скорость и радиус орбиты через обратно-пропорциональную связь. В результате Бор получил уравнение для электронных орбит водорода в виде:
(9) |
Однако, парадокс, допущенный Бором в том, что своим постулатом по дискретным орбитам он исключил излучение при движении электрона на дискретных орбитах, в то время как уравнение гармонического осциллятора именно основано на излучении, в виде значения ![]() .
.
Отметим, что с учётом нашей теории разница на ![]() , не позволяет представить длину и скорость как противоположности, с учётом условия охвата всех объектов Мироздания при взаимодействии. Величина радиуса в уравнении гармонического осциллятора характеризует систему наблюдения процесса в статике, но не определяет взаимодействие в преобразовании величин, так как является неизменной величиной. При этом использование радиуса при взаимодействии приводит к парадоксам, как, например, магнитная сила при движении заряда по окружности при неизменном радиусе не может осуществлять работы [10, с. 118-119]. Однако это означает существование силы без затрат энергии по второму закону Ньютона, чего быть не может. Иными словами, использовать неизменное значение радиуса как константы для описания динамики взаимодействия сил нельзя. Собственно, если перейти на учёт определения заряда по Дираку как:
, не позволяет представить длину и скорость как противоположности, с учётом условия охвата всех объектов Мироздания при взаимодействии. Величина радиуса в уравнении гармонического осциллятора характеризует систему наблюдения процесса в статике, но не определяет взаимодействие в преобразовании величин, так как является неизменной величиной. При этом использование радиуса при взаимодействии приводит к парадоксам, как, например, магнитная сила при движении заряда по окружности при неизменном радиусе не может осуществлять работы [10, с. 118-119]. Однако это означает существование силы без затрат энергии по второму закону Ньютона, чего быть не может. Иными словами, использовать неизменное значение радиуса как константы для описания динамики взаимодействия сил нельзя. Собственно, если перейти на учёт определения заряда по Дираку как: ![]() , и учесть, что минимальная масса покоя должна равняться шагу дискретизации, по нашей теории h=m0, то мы получим, что первая боровская орбита меньше, чем постоянная Планка
, и учесть, что минимальная масса покоя должна равняться шагу дискретизации, по нашей теории h=m0, то мы получим, что первая боровская орбита меньше, чем постоянная Планка ![]() . Это говорит о том, что использование систем измерения СГС или СИ, без учёта влияния среды, через константы электрической и магнитной проницаемости, даёт парадоксы. Отсюда правильная нормировка в динамике взаимодействия соответствует не радиусу, а длине окружности, по которой осуществляется взаимодействие. Действительно нельзя представить взаимодействие объектов без представления через изменение энергии (площади) по циклу Карно
. Это говорит о том, что использование систем измерения СГС или СИ, без учёта влияния среды, через константы электрической и магнитной проницаемости, даёт парадоксы. Отсюда правильная нормировка в динамике взаимодействия соответствует не радиусу, а длине окружности, по которой осуществляется взаимодействие. Действительно нельзя представить взаимодействие объектов без представления через изменение энергии (площади) по циклу Карно ![]() , а это изменение даёт значение длины окружности
, а это изменение даёт значение длины окружности ![]() . В результате, имеем:
. В результате, имеем:
(10) |
В (8) также было учтено, что при соответствующей нормировке уравнение гармонического осциллятора может быть приведено к виду:
![]() , (11)
, (11)
Перепишем полученное уравнение с учётом переноса:
![]() , (12)
, (12)
Далее произведем следующие преобразования:
(13) |
Последнее уравнение по виду аналогично уравнению преобразований Лоренца (в [2, с. 5-37] мы показали вывод уравнения окружности из преобразований Лоренца). И отсюда мы также можем получить соответствие с уравнением энергии Эйнштейна, если сделать замену переменных и считать, что m=1/v1, а m0=1/c. В итоге имеем:
(14) |
Если умножить оба члена указанного последнего уравнения на одинаковую величину c2=с/h=Nоб, то получим формулу энергии Эйнштейна в виде ![]() . Значение Nоб определяет общее количество элементарных объектов в мироздании при обмене и их взаимосвязи через скорость света. Соответственно мы видим, что энергия и масса выступают как противоположности, связанные обратно-пропорциональной связью, и фактически они заменяют соотношение неопределённостей Гейзенберга в детерминированном виде. Можно представить энергию Эйнштейна и в другом известном виде:
. Значение Nоб определяет общее количество элементарных объектов в мироздании при обмене и их взаимосвязи через скорость света. Соответственно мы видим, что энергия и масса выступают как противоположности, связанные обратно-пропорциональной связью, и фактически они заменяют соотношение неопределённостей Гейзенберга в детерминированном виде. Можно представить энергию Эйнштейна и в другом известном виде:
(15) |
Это означает, что из преобразований Лоренца по связи длины и времени, которые тоже связаны с формулой окружности, получается и уравнение энергии Эйнштейна.
Однако получение уравнения энергии Эйнштейна на основе соответствия общей формуле мироздания касается корпускулярных свойств, но объект представляет собой сочетание корпускулярных и волновых свойств. Тогда следует вопрос: «Каким образом, общей формуле Мироздания должны соответствовать законы физики, определяющие волновые свойства и как они связаны с корпускулярными свойствами?» Собственно эту задачу попытался решить Шредингер, на основе уравнения Гамильтона-Якоби, и Дирак на основе уравнения энергии Эйнштейна, которая уже связана с общей формулой Мироздания. Дирак интуитивно предложил переход от корпускулярных свойств к волновым свойствам через уравнение энергии Эйнштейна на основе волновых функций Луи де Бройля [6, с. 216-217], которые формируют общее уравнение Мироздания.
В этом случае первоначальное уравнение энергии Эйнштейна с учётом «линеаризации» имеет вид [11, с. 295-298]:
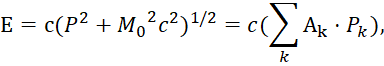 | (16) |
Здесь k изменяется от 0 до 3; P0=M0c; P1=Px; P2=Py; P3=Pz. Из этой записи при использовании матриц для разложения (16):
| (17) |
Следуют известные уравнения, которые дают систему уравнений Дирака. При этом система уравнений имеет вид:
(18) |
Далее конкретные числовые значения заменяются дифференциальными операторами с наличием мнимой единицы в виде:
(19) |
Которые должны воздействовать на волновую функцию Ψ, и которая, в свою очередь, характеризует вероятность. В дифференциальном виде мы получим систему уравнений Дирака:
(20) |
Понятно, что при «линеаризации» Дирак не опирался на реальные физические процессы для получения уравнения энергии Эйнштейна вида (7) и использовал функции, которые характеризуют вероятность вида:
![]() , (21)
, (21)
Такой вид соответствует функции Луи де Бройля для объектов Мироздания в отдельном замкнутом виде [6, с. 216-217]. Действительно, способ отражения корпускулярно-волновых свойств, исходя из функции Луи де Бройля, с соответствующим представлением значения Ψ0 по геометрии Минковского [12, с. 226] через экспоненциальные функции с учётом нижней формулы в (6) и формул Эйлера, можно представить в виде:
(22) |
Здесь значение Ψ0, отображает пространственно-временное искривление по геометрии Минковского в одной противоположности, что означает волновой процесс в другой противоположности в зависимости от частоты. При движении частицы имеем более общий случай:
![]() , (23)
, (23)
Здесь: ![]() . Понятно, что разница связана только с пересчётом переменных в виде:
. Понятно, что разница связана только с пересчётом переменных в виде: ![]() .
.
Так как постоянная Планка ћ присутствует при дифференцировании во всех членах, то её можно исключить из дальнейшего рассмотрения. Одновременно величина Ψ0, также может быть нормирована к единичному значению. Нормировка к единичному значению связана и с соответствием волновых функций Луи де Бройля формуле Мироздания, так как в этом случае ![]() . Соответственно имеем вид функций при движении частицы без наличия внешних сил:
. Соответственно имеем вид функций при движении частицы без наличия внешних сил:
![]() , (24)
, (24)
Следует заметить, что с учётом нашей теории и геометрии Минковского из величины ![]() получается известная формула Луи де Бройля [13, с. 63]:
получается известная формула Луи де Бройля [13, с. 63]:
(25) |
Кроме того, формула Луи де Бройля подтверждена экспериментально Девиссоном и Джермером в 1927 году, а это означает, что мы имеем физический закон, который не может быть вероятностным (случайным). Из этого следует, что функции Луи де Бройля должны быть выражены через реальные волновые функции, какими являются электромагнитные функции. Однако продолжим рассмотрение системы уравнений Дирака, и здесь при выражении одних функций через другие, с учётом дифференцирования для свободной частицы без внешнего электромагнитного поля, получаем:
(26) |
Сокращая на волновую вероятностную функцию Ψ1 (это означает учёт только корпускулярных свойств объекта), получаем уравнение энергии Эйнштейна для взаимодействующих противоположных частиц:
(27) |
Аналогичный результат мы имеем и для других волновых функций. Таким образом, мы видим, что Дирак фактически показал переход от уравнения движения частицы через волновые функции Луи де Бройля, которые также соответствуют общей формуле Мироздания (5), и как мы показали в [1, с. 7-38] формуле гармонического осциллятора. При этом получить указанный переход без наличия в системе уравнений Дирака мнимой единицы невозможно. Иными словами, в системе уравнений Дирака, таким образом, характеризуется корпускулярно-волновой дуализм, то есть представление объекта через противоположности. Собственно необходимость этого шага отражено и в квантовой механике и такое разделение противоположностей было введено физиками в виде x4=ict для длины и времени, и для векторных потенциалов в виде iФ=А4 [14, с. 317]. Кроме того, Дирак также применил в своей системе уравнений операторы (19) с мнимой единицей, и физически это означает, что при изменениях осуществляется переход в противоположность.
Однако следует отметить, что в системе уравнений Дирака (18) и (20), при описании корпускулярно-волнового объекта, волновые функции Ψ являются независимыми функциями в силу того, что они не имеют связи с окружающей средой распространения. Здесь нет их зависимости от параметров самой среды, как это, например, есть для электромагнитных волновых функций через константы электрической (![]() ) и магнитной (
) и магнитной (![]() ) проницаемости. Соответственно через такие функции Ψ выразить взаимодействие через излучение и поглощение невозможно в силу того, что функции Ψ связаны только с параметрами самой частицы через аргументы функций и соответственно их нет в самой среде распространения, так как нет зависимости функций от параметров среды распространения. Это исключает взаимодействие через обмен и соответственно при этом нарушается принцип Гюйгенса – Френеля. Понятно, что альтернативой волновым функциям Ψ, которые характеризуют вероятность, являются только волновые электромагнитные реальные функции. Отсюда необходимо показать, как система уравнений Дирака с учётом наличия волнового представления через функции Луи де Бройля связана с известными законами электродинамики, а значит с электромагнитными волновыми составляющими. В этом случае, надо показать, каким образом электромагнитные волновые функции, без нарушения законов электродинамики, могут быть представлены в системе уравнений Дирака. В противном случае через вероятностные волновые функции Ψ мы будем иметь чудеса, связанные с телепортацией, за счёт исключения распространения в среде, что, кстати, и было сделано физиками. Понятно, что если опираться на обычные уравнения Максвелла, то получить указанную взаимосвязь невозможно, именно с этой проблемой столкнулся Эйнштейн, когда пытался объединить СТО и ОТО с электромагнетизмом в общей единой теории. Отсюда было необходимо понять, что мешало такому объединению?
) проницаемости. Соответственно через такие функции Ψ выразить взаимодействие через излучение и поглощение невозможно в силу того, что функции Ψ связаны только с параметрами самой частицы через аргументы функций и соответственно их нет в самой среде распространения, так как нет зависимости функций от параметров среды распространения. Это исключает взаимодействие через обмен и соответственно при этом нарушается принцип Гюйгенса – Френеля. Понятно, что альтернативой волновым функциям Ψ, которые характеризуют вероятность, являются только волновые электромагнитные реальные функции. Отсюда необходимо показать, как система уравнений Дирака с учётом наличия волнового представления через функции Луи де Бройля связана с известными законами электродинамики, а значит с электромагнитными волновыми составляющими. В этом случае, надо показать, каким образом электромагнитные волновые функции, без нарушения законов электродинамики, могут быть представлены в системе уравнений Дирака. В противном случае через вероятностные волновые функции Ψ мы будем иметь чудеса, связанные с телепортацией, за счёт исключения распространения в среде, что, кстати, и было сделано физиками. Понятно, что если опираться на обычные уравнения Максвелла, то получить указанную взаимосвязь невозможно, именно с этой проблемой столкнулся Эйнштейн, когда пытался объединить СТО и ОТО с электромагнетизмом в общей единой теории. Отсюда было необходимо понять, что мешало такому объединению?
Собственно решение по объединению фактически уже было применено и в классической электродинамике с введением сторонних (фиктивных) токов и зарядов. При этом необходимо вспомнить, что одним из начальных законов электродинамики послужил закон Фарадея, который с учётом поправок Максвелла для среды распространения в дифференциальной форме выглядит в системе МКСА в виде [15, с. 26-28]:
![]() , (28)
, (28)
Слева от знака равенства мы имеем замкнутое электрическое поле, которое на практике даёт в замкнутом проводнике электродвижущую силу с наличием тока.
Но, кроме того, известен закон Ампера в дифференциальной форме [16, с. 29]:
![]() , (29)
, (29)
Однако в этом случае эта формула вопреки практике не может быть справедливой в нестационарном варианте (и это не наше утверждение), поскольку из него следует, что ![]() тогда как согласно уравнению непрерывности:
тогда как согласно уравнению непрерывности:
![]() , (30)
, (30)
Иными словами, изменение в пространстве означает и изменение во времени, а при замкнутых величинах от ротора (rot) изменения в пространстве нет. Поэтому физики и без нас были вынуждены ввести некий вектор ![]() определяющий зависимость магнитного поля в среде распространения в виде:
определяющий зависимость магнитного поля в среде распространения в виде:
![]() , (31)
, (31)
Понятно, что в данном случае мы не исключаем парадокс неоднозначности, связанный с тем, что с одной стороны изменение во времени от величины С даёт замкнутый процесс без изменения в пространстве, а с другой стороны изменение величины С должно быть связано с изменением в пространстве плотности тока, так как исходя из (29) получаем:
![]() , (32)
, (32)
Согласно теореме Гаусса в дифференциальной форме [17, с. 27]:
![]() , (33)
, (33)
Отсюда следует, что:
![]() , (34)
, (34)
Соответственно, отсюда получаем:
![]() , (35)
, (35)
В итоге мы видим симметрию относительно электромагнитных составляющих с учётом параметров среды в виде констант электрической и магнитной проницаемости. При этом значения Е и Н выражены в векторном виде по пространству. Однако видно, что обычные уравнения Максвелла не решают проблему парадокса, при котором изменения электромагнитных составляющих по времени не дают изменения по пространству из-за замкнутости по ротору. Собственно такой парадокс исключает взаимосвязь длины и времени по СТО и ОТО Эйнштейна с соблюдением закона сохранения количества. Это проявилось при отображении волнового вида с использованием обычных уравнений Максвелла. Так, для получения волнового вида распространения в пространстве уравнение (35) дифференцируют (изменяют) по времени с перестановкой переменных дифференцирования как ортогональных величин и получают:
![]() , (36)
, (36)
С учётом подстановки уравнения (29), что означает взаимосвязь переменных, следует вид:
![]() , (37)
, (37)
Поскольку в среде распространения зарядов (соответственно и токов) нет, то физики утверждают, что ![]() , отсюда:
, отсюда:
![]() , (38)
, (38)
В итоге имеем уравнение волны вида:
![]() , (39)
, (39)
Однако данный вид волны представляет собой движение брошенного камня и не может изменять направление движения, что не соответствует огибанию волной препятствия по принципу Гюйгенса – Френеля. Более того, как мы показали в [1, с. 7-38] деление на ![]() и
и ![]() , это чистое предположение физиков, так как математически отличие только в знаках. Это говорит о том, что представление векторов электрической и магнитной напряжённости только по пространству не является полным, что, кстати, бы означало их не подчинение преобразованиям Лоренца - Минковского, а также не соответствовало замкнутой системе Мироздания. Отсюда следует вывод о том, что напряжённости электрических и магнитных полей должны как объекты Мироздания быть выражены в проекциях двух противоположностей, то есть по пространству и времени, а иначе следует их независимость от нашей системы Мироздания. Понятно, что на этот парадокс также обратили внимание физики и ввели так называемые токи смещения (сторонние токи или фиктивные токи). Собственно, по этой причине физики заявили, что согласно специальной теории относительности, физические законы не должны зависеть от выбора лоренцевой системы координат. Поэтому уравнения Максвелла, как и уравнения Дирака должны быть инвариантными относительно преобразований Лоренца [18, с. 300]. При этом плотность стороннего заряда и тока (ничего другого в среде распространения нет) отображаются четырёхмерным вектором в виде:
, это чистое предположение физиков, так как математически отличие только в знаках. Это говорит о том, что представление векторов электрической и магнитной напряжённости только по пространству не является полным, что, кстати, бы означало их не подчинение преобразованиям Лоренца - Минковского, а также не соответствовало замкнутой системе Мироздания. Отсюда следует вывод о том, что напряжённости электрических и магнитных полей должны как объекты Мироздания быть выражены в проекциях двух противоположностей, то есть по пространству и времени, а иначе следует их независимость от нашей системы Мироздания. Понятно, что на этот парадокс также обратили внимание физики и ввели так называемые токи смещения (сторонние токи или фиктивные токи). Собственно, по этой причине физики заявили, что согласно специальной теории относительности, физические законы не должны зависеть от выбора лоренцевой системы координат. Поэтому уравнения Максвелла, как и уравнения Дирака должны быть инвариантными относительно преобразований Лоренца [18, с. 300]. При этом плотность стороннего заряда и тока (ничего другого в среде распространения нет) отображаются четырёхмерным вектором в виде:
(40) |
Так как сторонние токи и заряды по определению физиков относятся к четырёхмерным векторам, то отсюда следует необходимость включения в уравнения Максвелла наличие проекций на время и уравнения (29) и (36) имеют вид:
(41) |
Оставалось только признать, что, так как сторонние токи реально не наблюдались в пространстве, то следует признать их отображение в проекции на время, что, собственно, и было сделано Фейнманом, но при использовании векторных (электродинамических) потенциалов [19, с. 271]. Как отмечено выше в силу симметрии между противоположностями с соблюдением закона сохранения количества и законов физики мы распространили проекцию на время и для электромагнитных составляющих. Иное даёт независимость электромагнитных составляющих от пространственно-временного искривления, а также векторных потенциалов, и как следствие будет отсутствовать принцип Гюйгенса-Френеля с изменением направления движения света. Иными словами, решение указанного выше парадокса связанно с тем, что замкнутому процессу в виде ротора в одной противоположности соответствует процесс наличия уравнения непрерывности в другой противоположности.
При этом соблюдается условие преобразования проекции длины на время, и наоборот, по СТО и ОТО Эйнштейна. Однако данное преобразование связано с взаимодействием через обмен, а это подразумевает преобразование в иной вид. В электродинамике преобразование из волнового вида характеризуется как источник излучения или поглощения, а само преобразование из корпускулярного вида в волновой вид, и наоборот, связано со сменой закономерностей. И такое преобразование подчиняется формулам Эйлера в виде:
(42) |
Именно поэтому физики были вынуждены использовать мнимую единицу (i) для констант электрической и магнитной проницаемости [20, с. 117-191], чтобы показать излучение и поглощение. При этом электромагнитные составляющие стали соответствовать четырёхмерным векторам. Таким образом, физики уже до нас на практике стали использовать мнимую единицу в уравнениях Максвелла, мы лишь только указали, что это решает парадокс. В итоге система усовершенствованных уравнений Максвелла приобрела векторный вид:
(43) |
Надо отметить, что в данную систему уравнений значение тока как результата от движения реальных зарядов не входит в силу того, что в этом случае нарушается равенство между правыми и левыми частями первых двух уравнений в (43). Собственно этот парадокс и был обнаружен самими физиками на основании ![]() . Поэтому наличие стороннего тока решает и частную задачу по выполнению закона Био – Савара. Так как в соответствии с СТО Эйнштейна при движении всегда есть проекция электромагнитных полей на время, которую можно связать в стационарном случае с формированием замкнутого магнитного поля. В частных производных усовершенствованные уравнения Максвелла можно представить как:
. Поэтому наличие стороннего тока решает и частную задачу по выполнению закона Био – Савара. Так как в соответствии с СТО Эйнштейна при движении всегда есть проекция электромагнитных полей на время, которую можно связать в стационарном случае с формированием замкнутого магнитного поля. В частных производных усовершенствованные уравнения Максвелла можно представить как:
(44) |
Собственно, мы не придумали ничего нового, а в соответствии с логикой того, что сторонние токи и заряды не имеют представления в пространстве, но вытекают из элементарной логики, что показано в [1, с. 7-38], представили их в виде проекций на время с отображением преобразований через мнимую единицу. Соответственно ничего проще для описания реальных объектов представить нельзя, так как в любом случае объект Мироздания в одной противоположности должен описываться для своей индивидуальности (независимости) как замкнутый процесс (ротор), а в другой противоположности для взаимодействия и обмена как разомкнутый процесс (уравнение непрерывности). То есть, данное представление и взаимодействие должно описывать реальные объекты и надо сказать, что и здесь мы не «изобретали велосипед». Схожий вид уравнений следовал из системы уравнений Дирака, при массе покоя равной нулю. Отсутствие массы покоя автоматически означает движение со скоростью света, так как противоположности отражаются через корпускулярный вид с массой покоя и волновой вид без массы покоя. При этом противоположности связаны через скорость света. В этом случае в квантовой механике для описания нейтрино и антинейтрино используется уравнение с двухрядными матрицами Паули (уравнение Вейля), либо система уравнений Дирака, с расщеплением на независимые уравнения [21, с. 355]:
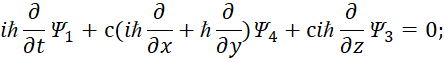 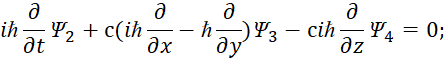 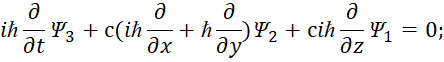 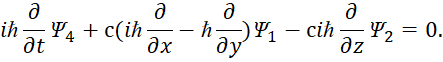 | (45) |
Однако данная система уравнений никак не подходила для описания электромагнитных процессов в силу наличия трёх функций в уравнениях вместо двух функций, поэтому физики придумали свою интерпретацию, показанную на рисунке 2.
Рис. 2. Нейтрино и антинейтрино
Здесь введено понятие левой и правой «материи», которые не имеют в теории никакого физического обоснования, так как не имеют математического описания с наличием количества, и это связано с отсутствием понимания учёными происходящих в мироздании процессов. Следует обратить внимание на то, что первое и третье уравнение в системе (45), имеют отличия только в обозначении функций в виде (![]() ) и (
) и (![]() ). Аналогично, мы имеем отличия в обозначении функций для второго и четвёртого уравнения в виде (
). Аналогично, мы имеем отличия в обозначении функций для второго и четвёртого уравнения в виде (![]() ) и (
) и (![]() ). При этом волновые функции Ψ Луи де Бройля при соответствии уравнению энергии Эйнштейна в системе Дирака, и без учёта редуцированной постоянной Планка (ћ), которая сокращается, имеют вид (24):
). При этом волновые функции Ψ Луи де Бройля при соответствии уравнению энергии Эйнштейна в системе Дирака, и без учёта редуцированной постоянной Планка (ћ), которая сокращается, имеют вид (24): ![]() . Причём в силу того, что для взаимодействия осуществляется подстановка с выражением одних функций через другие, и здесь идёт описание через параметры одной общей частицы, то значения в аргументах функций Ψ должны быть одинаковыми. А это означает, что различий по функциям нет! Отсюда отличий между первым и третьим уравнением, а также вторым и четвёртым уравнениями – нет! Понятно, что это означает парадокс однородности с отсутствием противоположностей через функции. В этом случае остаётся отличие между первым и третьим уравнениями с одной стороны, и вторым и четвёртым уравнениями с другой стороны, только по знакам плюс или минус. Одинаковый вид функций означает неоднозначность в уравнениях, так как сложение в одном уравнении при тех же функциях равно вычитанию в другом уравнении. Иными словами, с точки зрения математики получается 5+5=5-5. Это означает, что должно быть разрешение указанного парадокса в реальности. При этом логика представления электронных и мюонных нейтрино (антинейтрино) должна быть основана на практике распада корпускулярных частиц с превращением массы покоя в ноль. Отсюда, чтобы разобраться в физических процессах, происходящих в ядре, необходимо сначала проанализировать известные практические схемы распада [22, с. 277]:
. Причём в силу того, что для взаимодействия осуществляется подстановка с выражением одних функций через другие, и здесь идёт описание через параметры одной общей частицы, то значения в аргументах функций Ψ должны быть одинаковыми. А это означает, что различий по функциям нет! Отсюда отличий между первым и третьим уравнением, а также вторым и четвёртым уравнениями – нет! Понятно, что это означает парадокс однородности с отсутствием противоположностей через функции. В этом случае остаётся отличие между первым и третьим уравнениями с одной стороны, и вторым и четвёртым уравнениями с другой стороны, только по знакам плюс или минус. Одинаковый вид функций означает неоднозначность в уравнениях, так как сложение в одном уравнении при тех же функциях равно вычитанию в другом уравнении. Иными словами, с точки зрения математики получается 5+5=5-5. Это означает, что должно быть разрешение указанного парадокса в реальности. При этом логика представления электронных и мюонных нейтрино (антинейтрино) должна быть основана на практике распада корпускулярных частиц с превращением массы покоя в ноль. Отсюда, чтобы разобраться в физических процессах, происходящих в ядре, необходимо сначала проанализировать известные практические схемы распада [22, с. 277]:
(46) |
Здесь ![]() ‒ электронное нейтрино и антинейтрино,
‒ электронное нейтрино и антинейтрино, ![]() ‒ мюонное нейтрино и антинейтрино соответственно,
‒ мюонное нейтрино и антинейтрино соответственно, ![]() – фотоны (кванты). Существуют и другие схемы распада, но они все заканчиваются на электронах е+, позитронах е‒, фотонах и электронных и мюонных нейтрино (антинейтрино). При этом известно, что электрон и позитрон, при аннигиляции также дают фотоны (масса покоя равна нулю). Из первых двух схем распада с положительным и отрицательным мюоном по формулам (46) видно, что дополнительная масса покоя положительного мюона связана с наличием электронного нейтрино (
– фотоны (кванты). Существуют и другие схемы распада, но они все заканчиваются на электронах е+, позитронах е‒, фотонах и электронных и мюонных нейтрино (антинейтрино). При этом известно, что электрон и позитрон, при аннигиляции также дают фотоны (масса покоя равна нулю). Из первых двух схем распада с положительным и отрицательным мюоном по формулам (46) видно, что дополнительная масса покоя положительного мюона связана с наличием электронного нейтрино (![]() ) и мюонного антинейтрино (
) и мюонного антинейтрино (![]() ). Дополнительная масса покоя отрицательного мюона связана с наличием электронного антинейтрино (
). Дополнительная масса покоя отрицательного мюона связана с наличием электронного антинейтрино (![]() ) и мюонного нейтрино (
) и мюонного нейтрино (![]() ). При этом, с точки зрения туннельного эффекта в квантовой механике, такой распад не имеет объяснения. Действительно, в этом случае надо найти механизм, каким образом электронные и мюонные нейтрино и антинейтрино взаимодействуют и удерживаются ядерными силами, которые должны быть у электронов и позитронов. Здесь нет формул взаимодействия, при этом следует напомнить, что электронные и мюонные нейтрино на основании практических результатов имеют скорость движения равной скорости света. Такая скорость действительна только для электромагнитных составляющих в соответствии с обычными или усовершенствованными уравнениями Максвелла. Соответственно, каким образом будет происходить торможение электронного или мюонного нейтрино (антинейтрино) в одном направлении и получение им составляющих в другом направлении под действием энергетического барьера из ядерных сил? И что собой должен представлять этот ядерный потенциальный барьер? Это неразрешимые парадоксы квантовой механики. Соответственно телепортация вообще исключает взаимодействие.
). При этом, с точки зрения туннельного эффекта в квантовой механике, такой распад не имеет объяснения. Действительно, в этом случае надо найти механизм, каким образом электронные и мюонные нейтрино и антинейтрино взаимодействуют и удерживаются ядерными силами, которые должны быть у электронов и позитронов. Здесь нет формул взаимодействия, при этом следует напомнить, что электронные и мюонные нейтрино на основании практических результатов имеют скорость движения равной скорости света. Такая скорость действительна только для электромагнитных составляющих в соответствии с обычными или усовершенствованными уравнениями Максвелла. Соответственно, каким образом будет происходить торможение электронного или мюонного нейтрино (антинейтрино) в одном направлении и получение им составляющих в другом направлении под действием энергетического барьера из ядерных сил? И что собой должен представлять этот ядерный потенциальный барьер? Это неразрешимые парадоксы квантовой механики. Соответственно телепортация вообще исключает взаимодействие.
Если учесть, что антинейтрино и нейтрино это противоположности в Мироздании по формуле (6), что означает, что сложение в одной противоположности выглядит вычитанием в другой противоположности, то первое и третье уравнения, по отношению ко второму и четвёртому уравнениям в системе (45), отражают представление в противоположностях в общей системе наблюдения. Исключение массы покоя означает распад, и единственный вариант по (46) это переход в объекты с движением со скоростью света, что соответствует представлению через две функции в виде электрической и магнитной составляющей. Это означает что в системе уравнений (45) происходит преобразование, так как отсутствие изменений исключает и сам распад, и в этом случае в системе уравнений (45) уже должна наблюдаться взаимосвязь двух функций вместо трёх. Собственно переход к двум функциям это не наша выдумка, а было введено в квантовой механике для нейтрино и антинейтрино в виде уравнений Вейля [21, с. 355]. Понятно, что антинейтрино и нейтрино должны отображать наипростейшее взаимодействие между двумя глобальными противоположностями. А это означает отображение объекта в одной противоположности через обмен с внешними объектами (разомкнутость), так как иначе он не существует для других объектов, и собственный внутренний обмен в другой противоположности (замкнутость), иначе он будет распадаться. Математически это означает связь уравнения непрерывности (разомкнутость), например, через магнитные составляющие, характеризующие одну противоположность, и в виде замкнутости через ротор (rot), в другой противоположности через электрические составляющие по уравнениям (44). Понятно, что меньше, чем четырёх членов в наипростейшем уравнении, отражающий реальный объект, быть не может. Кроме того, нейтрино и антинейтрино должны иметь отличия в пространственно-временном представлении вне зависимости от точки наблюдения. Понятно, что изменение направления ротора по часовой стрелке или против часовой стрелки не может отражать разницу между нейтрино и антинейтрино, так как здесь есть зависимость от точки наблюдения. В этом случае и нужна проекция электромагнитных функций на время в усовершенствованных уравнениях Максвелла (44), и знак у этой проекции однозначно даёт разницу между нейтрино и антинейтрино в любой точке наблюдения в пространстве. При этом взаимодействие противоположностей связано с преобразованием входящих величин, а это фактически характеризует смену излучения на поглощение, что математически отображается через вычитание и сложение. Но для выполнения закона сохранения количества между противоположностями при сложении и вычитании необходимо иметь смену закономерностей, что происходит благодаря мнимой единице (i), в зависимости от системы наблюдения. Понятно, что таким образом через данные элементарные объекты получается замкнутый обменный процесс, иначе это не противоположности.
Однако, если различие между нейтрино и антинейтрино по (45) ещё можно объяснить, на основании разницы в знаках в общей системе наблюдения, то различие на электронное и мюонное нейтрино (антинейтрино) с использованием функций Ψ, характеризующих вероятность, система уравнений Дирака обеспечить не может (нет разницы по аргументам функций). Поэтому продолжим наши логические рассуждения. На основании логики при распаде мы можем представить изменения в системе (45) с учётом замены функций с трёх до двух через независимые уравнения:
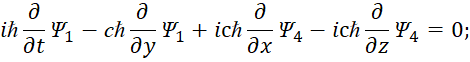 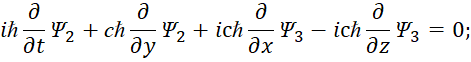 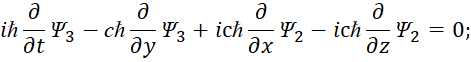 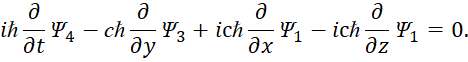 | (47) |
Суть преобразования в том, что, член производной по координате (у) в первом уравнении (45) в виде ![]() переставляется с членом производной из четвёртого уравнения
переставляется с членом производной из четвёртого уравнения 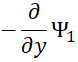 . Аналогичная замена и в других уравнениях с учётом получения уравнения непрерывности в соответствии с усовершенствованными уравнениями Максвелла. При этом произошла смена знаков. Далее при преобразовании у нас значение
. Аналогичная замена и в других уравнениях с учётом получения уравнения непрерывности в соответствии с усовершенствованными уравнениями Максвелла. При этом произошла смена знаков. Далее при преобразовании у нас значение ![]() во втором уравнении замещает член
во втором уравнении замещает член ![]() в первом уравнении. Однако, с учётом перестановки, член
в первом уравнении. Однако, с учётом перестановки, член ![]() , переходит из первого уравнения во второе уравнение с наличием смены знака в виде
, переходит из первого уравнения во второе уравнение с наличием смены знака в виде ![]() . Суть смены знака при перестановке относительно Ψ3 связана с тем, что нейтрино и антинейтрино, которые отображаются в первом и втором уравнениях, должны иметь помимо представления в виде разомкнутой составляющей через уравнение непрерывности, и замкнутую составляющую в виде ротора. Иначе нет отображения распада в реальных объектах, и просто перестановка членов не даёт преобразований. Отсюда прямое замещение с перестановкой через Ψ4 от второго уравнения в первое уравнение с одной стороны, при обратной перестановке Ψ3 имеет из первого уравнения во второе уравнение с другой стороны в системе (47) должно происходить со сменой знака через –Ψ3. Аналогичную перестановку по координате (z) мы имеем и для третьего и четвёртого уравнения. Это означает, что переход от свойств частицы к электронным и мюонным нейтрино (антинейтрино) связан не только с перестановкой и замещением членов в уравнениях с учётом закона сохранения количества, но и с изменением знака по одной из координат пространства. Собственно смена знака означает изменения в первоначальном взаимодействии, с отображением в ином виде за счёт смены закономерностей при соблюдении закона сохранения количества.
. Суть смены знака при перестановке относительно Ψ3 связана с тем, что нейтрино и антинейтрино, которые отображаются в первом и втором уравнениях, должны иметь помимо представления в виде разомкнутой составляющей через уравнение непрерывности, и замкнутую составляющую в виде ротора. Иначе нет отображения распада в реальных объектах, и просто перестановка членов не даёт преобразований. Отсюда прямое замещение с перестановкой через Ψ4 от второго уравнения в первое уравнение с одной стороны, при обратной перестановке Ψ3 имеет из первого уравнения во второе уравнение с другой стороны в системе (47) должно происходить со сменой знака через –Ψ3. Аналогичную перестановку по координате (z) мы имеем и для третьего и четвёртого уравнения. Это означает, что переход от свойств частицы к электронным и мюонным нейтрино (антинейтрино) связан не только с перестановкой и замещением членов в уравнениях с учётом закона сохранения количества, но и с изменением знака по одной из координат пространства. Собственно смена знака означает изменения в первоначальном взаимодействии, с отображением в ином виде за счёт смены закономерностей при соблюдении закона сохранения количества.
Сокращение функций до двух (Ψ1 и Ψ2, или Ψ3 и Ψ4) означает отсутствие связи через массу покоя, а наличие двух функций в уравнении характеризует необходимость наличия в объекте противоположностей. Сократив на постоянную Планка ћ, (по математике он не влияет на результат) и умножив на (–i), что означает переход в противоположную систему наблюдения за счёт преобразования, мы получим:
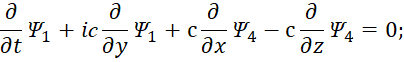 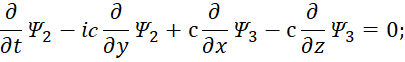 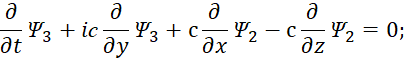 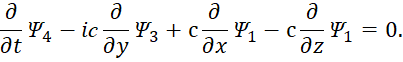 | (48) |
Иными словами, мы имеем четыре независимых уравнения, причём первое и третье уравнения, а также второе и четвёртое уравнение идентичны по виду и отличаются только обозначениями через функции Ψ. Данные уравнения (48) должны соответствовать наблюдаемому практическому распаду массы по (46) через электронные и мюонные нейтрино (антинейтрино) с учётом их взаимодействия с окружающей средой. При отсутствии взаимодействия их обнаружить в среде невозможно. Именно поэтому, по мнению физиков, функции Луи де Бройля Ψ могут иметь скорость превышающую скорость света. В этом есть парадокс в системе уравнений Дирака, так как в силу отсутствия связи с окружающей средой изменения в функциях Ψ касаются лишь свойств движущейся частицы через аргументы от её энергии и импульсов по координатам. Для решения парадокса остаётся предположить, что функции Ψ должны быть связаны с электромагнитными функциями с учётом известных законов физики по электродинамике. В противном случае мы имеем разрыв в преобразованиях, а это равносильно чуду. Следовательно, если исходить из усовершенствованных уравнений Максвелла (44), то для получения идентичности с (45) для первого и третьего уравнений мы можем выразить функции Ψ следующим образом:
  | (49) |
Иными словами, мы получаем физические аналоги реализаций функций Ψ1 и Ψ4, а также Ψ3 и Ψ2, выраженных через реальные электромагнитные составляющие по (44) с учётом констант электрической и магнитной проницаемости, то есть состояния среды. Это означает, что усовершенствованные уравнения Максвелла отражают реальные объекты в виде электронных и мюонных нейтрино и антинейтрино. Соответственно теперь надо понять, что реально означают константы электрической и магнитной проницаемости в среде распространения. С этой целью мы попытаемся объяснить необходимость первоначальной формулы, используемой в электродинамике по связи магнитных и электрических полей с точки зрения наличия противоположностей в любом объекте, которая имеет вид [23, с. 25]:
| (50) |
Здесь ![]() и
и ![]() константы магнитной и электрической проницаемости окружающей среды. На основании констант электрической и магнитной проницаемости в классической электродинамике в системе измерения СИ для характеристики среды распространения используется формула вычисления волнового сопротивления в виде [24, с. 299]:
константы магнитной и электрической проницаемости окружающей среды. На основании констант электрической и магнитной проницаемости в классической электродинамике в системе измерения СИ для характеристики среды распространения используется формула вычисления волнового сопротивления в виде [24, с. 299]:
![]() , (51)
, (51)
Однако для системы измерения СГС вообще нет констант электрической и магнитной проницаемости в окружающей среде (вакууме) и таким образом вакуум соответствует геометрии Эвклида. В системе СИ электрическая и магнитная составляющая волны в среде распространения отличаются друг от друга только количественно, и не являются противоположностями, как, например, длина и время, которые связаны по теории Минковского [12, с. 226] через скорость света (r=ct). А, если отличия только количественные, то это означает, что и законы физики должны быть одинаковые, чего на практике не наблюдается, так как нет никаких магнитных зарядов в пространстве, которые физики безуспешно ищут. Кроме того, отсутствие отличий между электрическими и магнитными составляющими исключает и взаимодействие, что соответствует противоположностям, так как для величин отличающихся только количественно происходит ассоциативное сложение или вычитание (принцип суперпозиции). Это означает парадокс, и отсюда следует, что должна быть иная интерпретация констант электрической и магнитной проницаемости, при которой мы имели представление электрических и магнитных составляющих как противоположностей. Учитывая скорость распространения электромагнитных волн со скоростью света, нам остаётся предположить, что электромагнитные составляющие относятся к противоположной системе наблюдения, где выполнение по преобразованиям Лоренца ‒ Минковского соблюдается на основе проекции скорости на время. Иными словами, среда распространения по СТО и ОТО Эйнштейна должна характеризоваться через пространственно-временное искривление, так как никаких иных компонентов для определения физических свойств среды на основе математических формул не предусмотрено, и все остальные характеристики имеют чисто выдуманный характер. В этом случае кинетическая энергия электромагнитной волны в противоположной системе наблюдения будет выражаться потенциальной энергией по ОТО Эйнштейна в нашей системе наблюдения через константы электрической и магнитной проницаемости, так как системы наблюдения отличаются на скорость света и покой в одной означает движение в другой.
Поэтому, нам следует выразить константы магнитной и электрической проницаемости через усреднённое (интегральное) движение частиц, со скоростью (кинетической энергией) в противоположной системе наблюдения ![]() , связанной с нашей системой наблюдения через скорость света. Усреднённое интегральное значение кинетической энергии от противоположности говорит о том, что любая частица в одной противоположности связана с взаимодействием и всеми частицами в другой противоположности. Собственно иной подход означал бы отсутствие учёта взаимодействия и обмена при учёте движения частиц. И это тоже не наша выдумка, так как на этом построена идея получения формулы Планка для замкнутой системы, которой является всё Мироздание, с исключением варианта «ультрафиолетовой катастрофы» [25, с. 27-31], и с использованием закона Больцмана вида
, связанной с нашей системой наблюдения через скорость света. Усреднённое интегральное значение кинетической энергии от противоположности говорит о том, что любая частица в одной противоположности связана с взаимодействием и всеми частицами в другой противоположности. Собственно иной подход означал бы отсутствие учёта взаимодействия и обмена при учёте движения частиц. И это тоже не наша выдумка, так как на этом построена идея получения формулы Планка для замкнутой системы, которой является всё Мироздание, с исключением варианта «ультрафиолетовой катастрофы» [25, с. 27-31], и с использованием закона Больцмана вида ![]() . По сути, это закон связи между распадом в одной противоположности и синтезом в другой противоположности. Отсюда имеем формулы для констант магнитной и электрической проницаемости в виде:
. По сути, это закон связи между распадом в одной противоположности и синтезом в другой противоположности. Отсюда имеем формулы для констант магнитной и электрической проницаемости в виде:
(52) |
В этом случае константы электрической и магнитной проницаемости не имеют аналогичный вид, а это даёт их представление как противоположностей, и при этом они отличаются на значение с2. Соответственно имеем представление (50) с подчинением ОТО Эйнштейна в виде:
(53) |
Понятно, что наличие констант электрической и магнитной проницаемости в окружающей среде должно определять и соответствующие параметры частиц в Мироздании, так как взаимодействие частиц происходит именно через параметры окружающей среды и именно баланс в обмене исключает распад частиц. Поэтому, как было показано в [1, с. 7-38], с учётом нашей теории масса протона вычисляется исходя из волнового сопротивления среды распространения с учётом максимума энергии излучения по формуле Планка при коэффициенте 4,965 [25, с. 27-31]. Здесь мы учитываем, что в отличие от системы СИ у нас отношение ![]() , а не просто число
, а не просто число ![]() [24, с. 299]. В итоге выше была получена формула:
[24, с. 299]. В итоге выше была получена формула:
![]() , (54)
, (54)
Некоторое небольшое отличие от практики (1836,1) в числовом значении есть, и оно связано с тем, что наши расчёты выполнены для более общего случая с делением только на протон и электрон. Кроме того, при динамике обмена обязательно должна быть энергия с соответствующей массой для излучения. Таким образом наша теория позволяет определить и разницу масс между протоном и электроном на основе СТО и ОТО Эйнштейна.
Это в корне отличается от концепции физиков, при котором протон состоит из кварков и глюонов по рисунку 1. Надо отметить, что усовершенствованные уравнения Максвелла (49), выраженные через закономерности, совпадают с видом общего уравнения Мироздания при ![]() . Это означает, что объекты внутри мироздания, при их наличии, поддерживаются за счёт общего баланса обмена, в динамике взаимодействия между противоположными составляющими.
. Это означает, что объекты внутри мироздания, при их наличии, поддерживаются за счёт общего баланса обмена, в динамике взаимодействия между противоположными составляющими.
Из показанной логики следует вывод, что усовершенствованные уравнения Максвелла являются простейшим отражением взаимодействия противоположностей и отражают реальные объекты в виде электронных и мюонных нейтрино.
Надо отметить, что так как усовершенствованные уравнения Максвелла представляют собой сочетание уравнения непрерывности с замыканием через проекцию на время, например, для электрической составляющей и ротора – для магнитной составляющей, и наоборот, то фактически мы имеем представление электрического и магнитного полей через электронные и мюонные нейтрино (антинейтрино). Иными словами, через взаимодействие электронных и мюонных нейтрино (антинейтрино) с окружающей средой через излучение и поглощение формируются стационарные электрические и магнитные поля. Действительно в пространстве мы можем наблюдать только напряжённость электрического (магнитного) поля от уравнения непрерывности при взаимодействии, а ротор от магнитного (электрического) поля в силу замкнутости не может дать взаимодействие в силу равенства составляющих. Понятно, что и это наше утверждение о силовом воздействии через электрические и магнитные поля не является выдуманным из головы, а также было отображено в классической электродинамике [26, с. 41-113] при попытке объяснения наличия давления света. Собственно данный вывод физиков основывался на силе Лоренца в системе Хевисайда – Лоренца вида:
![]() , (55)
, (55)
Однако как это давно принято у физиков данный переход не обошёлся без подгонок под результат. При этом физики считали, что при отсутствии вещества плотность силы Лоренца (а это отсутствие зарядов) может быть приведена к виду:
![]() , (56)
, (56)
Здесь:
![]() , (57)
, (57)
Практически член в (57) выражает последний член после знака равенства в формуле Лоренца (55). Иными словами, заряд, который по теории Дирака равен ![]() , и скорость (v), по собственному желанию, заменили напряжённостью электрического поля. При этом под знак производной по времени ввели произвольно ещё и напряжённость магнитного поля. В итоге получили член, определяющий изменение плотности энергии во времени, который не имеет ничего общего с первоначальным определением силы Лоренца направленной перпендикулярно к магнитному полю и скорости движения заряда. Понятно, что
, и скорость (v), по собственному желанию, заменили напряжённостью электрического поля. При этом под знак производной по времени ввели произвольно ещё и напряжённость магнитного поля. В итоге получили член, определяющий изменение плотности энергии во времени, который не имеет ничего общего с первоначальным определением силы Лоренца направленной перпендикулярно к магнитному полю и скорости движения заряда. Понятно, что ![]() тензор напряжений Максвелла характеризует первый член после знака равенства в (55), который также отражает, по произвольному решению физиков, изменение энергии в пространстве. В компонентах по координатам и времени мы имеем вид:
тензор напряжений Максвелла характеризует первый член после знака равенства в (55), который также отражает, по произвольному решению физиков, изменение энергии в пространстве. В компонентах по координатам и времени мы имеем вид:
![]() , (58)
, (58)
Соответственно в этом случае тензор описывается в виде:
![]() , (59)
, (59)
Здесь ![]() – символ Кронекера.
– символ Кронекера.
Далее физики считают, что при усреднении по времени (56) член ![]() исчезает и для средней плотности силы имеем:
исчезает и для средней плотности силы имеем:
![]() , (60)
, (60)
Полученной, таким образом, силе приписывается роль силы давления света. По сути, формула (56) отображает закон, по которому неравенство изменения энергии по времени с изменением по пространству равносильно появлению силы. Однако тут возникает парадокс, связанный с тем, что изменение энергии во времени должно равняться изменению энергии в пространстве [27, с. 44], так как иное означает чудо появление энергии из ничего и исчезновение в ноль. То есть, не соблюдается закон сохранения количества по формуле Умова – Пойтинга:
![]() , (61)
, (61)
Понятно, что формула (57) парадоксальна и противоречит формуле (61). Это означает, что вывод давления света из формулы Лоренца не соответствует действительности. Однако понятно, что раз существует давление света и присутствует закон Лоренца, наблюдаемый на практике, то должна быть связь усовершенствованных уравнений Максвелла, отражающих электронные и мюонные нейтрино (антинейтрино) с силой Лоренца (55), так как иначе не будет воздействия этих элементарных объектов. Если предполагать что-то иное, то надо иметь реальное представление через объекты взаимодействия с подчинением формуле Мироздания. Собственно закон Лоренца, с учётом представления заряда ![]() , в виде распределения компонент в пространстве можно представить в системе МКСА в виде:
, в виде распределения компонент в пространстве можно представить в системе МКСА в виде:
(62) |
Далее, если рассматривать относительность по СТО Эйнштейна, где объект отождествляется с так называемым зарядом, то мы можем представить не движение заряда, который как бы находится в покое, а изменение магнитного поля. Отсюда вид (62) может быть получен из закона Фарадея [28, с. 27] где в частных производных мы имеем:
![]() , (63)
, (63)
Дифференциалы на практике можно заменить приращениями ![]() , так как бесконечно малых величин в Мироздании нет (это противоречит постоянной Планка), тогда перепишем:
, так как бесконечно малых величин в Мироздании нет (это противоречит постоянной Планка), тогда перепишем:
![]() , (64)
, (64)
По правилам математики, умножим члены уравнения на ![]() , и получим:
, и получим:
![]() , (65)
, (65)
Далее рассмотрим вариант, когда в нашей системе есть объекты, подчиняющиеся СТО Эйнштейна с движением. При этом будем считать, что ![]() , а
, а ![]() (нет движения между х и у, что означает изотропность). Соответственно будем иметь уравнение:
(нет движения между х и у, что означает изотропность). Соответственно будем иметь уравнение:
![]() , (66)
, (66)
Переходя от приращений к самим величинам, мы получаем (62) с учётом умножение на заряд.
Иными словами сила Лоренца по (55) отражает закон Фарадея, но в иной форме представления из соответствующей системы наблюдения, связанной с объектом. Однако, как мы показали выше, закон Фарадея имеет парадокс, связанный с тем, что замкнутая величина слева от знака равенства, формируется за счёт изменения по времени, что противоречит уравнению Умова – Пойтинга (61). Отсюда следовала необходимость усовершенствования уравнений Максвелла с учётом соблюдения СТО и ОТО Эйнштейна. Кроме того, с практической точки зрения сила Лоренца по (55) никак не могла дать давление света, так как для давления необходимо было иметь причину в виде силы, а это связано с градиентом изменения по пространству, что и было нами исправлено за счёт проекций электромагнитных составляющих на время (44) с учётом подчинения уравнений СТО и ОТО Эйнштейна. Таким образом, мы видим, что обычные уравнения Максвелла в принципе не отвечают практическому результату, связанному с наличием давления света. Кроме того, описать наличие отдельных магнитных и электрических сил без градиента по пространству невозможно, и для этого также необходима проекция электромагнитных составляющих на время, чего нет в обычных уравнениях Максвелла.
Однако, свет – это фотоны, но не сами электронные и мюонные нейтрино (антинейтрино). Поэтому, теперь необходимо показать, как на основании этих уравнений получаются фотоны, электроны и позитроны при взаимодействии. Собственно, здесь мы также ничего не изобретали. Так при взаимодействии усовершенствованных уравнений Максвелла были получены уравнения для электромагнитной волны [1, с. 7-38]:
(67) |
Физически это означает, что волновые свойства в одной противоположности определяются динамикой изменения сторонних токов и зарядов, которые в другой противоположности выражают реальное движение частиц. Понятно, что если вместо волнового уравнения слева от знака равенства в (67) будет источник или поглотитель, то мы получим вид вторых и четвертых уравнений в системе Дирака, что характеризует волну с подчинением принципу Гюйгенса-Френеля. Такой вид – это тоже не наша выдумка и он был использован физиками в квантовой механике в виде [29, с. 30-31]:
![]() , (68)
, (68)
Понятно, что и в классической электродинамике получили аналогичный вид, но для этого использовали векторные потенциалы, которые были связаны с электромагнитными составляющими и фактически отражали те же самые усовершенствованные уравнения Максвелла, но в противоположности в виде:
(69) |
Здесь учитывается, что в соответствии с классической электродинамикой мы имеем формулу связи векторных потенциалов из электродинамики [30]:
![]() , (70)
, (70)
При этом скорость распространения соответствует значению скорости света ![]() .
.
Отметим, что физики при использовании систем измерения СИ или СГС не могли прийти к наличию последнего уравнения (69) из-за отсутствия равенства между Е и Н через скорость света по формуле (51), что характеризует эти компоненты как противоположности.
В частных производных мы имеем вид:
(71) |
Здесь, мы имеем мнимую единицу i=(‒1)1/2, при проекции Ф на время, которая также связана с исключением парадокса обнуления по математике.
Исходя из векторных потенциалов, которые в противоположности характеризуют усовершенствованные уравнения Максвелла, в классической электродинамике нами были получены волновые уравнения для векторных потенциалов с источниками возбуждения в виде сторонних токов [1, с. 7-38]:
(72) |
Здесь ![]() .
.
Это означает, что мы имеем обратно - пропорциональную зависимость между сторонними электрическими и магнитными токами, которая совпадает с обратно-пропорциональной зависимостью для объектов длины и времени по СТО Эйнштейна с соблюдением инвариантности. По сути дела, исходя из значений констант электрической и магнитной проницаемости мы получаем, что в уравнениях волны через векторные потенциалы А и Ам=Ф отображаются значения электрической и магнитной индукции в соответствующей системе наблюдения. Однако отметим вид уравнений (72) не может дать равенства в силу того, что слева от знака равенства присутствует волновая функция, а справа от знака равенства она отсутствует и есть числовое значение. Собственно этот парадокс решается, так как по усовершенствованным уравнениям Максвелла (43) сторонние электрические и магнитные токи связаны с изменением электрической и магнитной индукции которые отображаются, как и функции Луи де Бройля в комплексном виде.
В итоге с учётом смены системы наблюдения на противоположную систему, когда масса и скорость в противоположностях меняются местами (это фактически ввёл Бор с учётом обратно-пропорциональной связи и следует также из нашей теории), при ![]() имеем вид уравнений:
имеем вид уравнений:
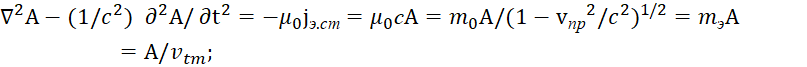 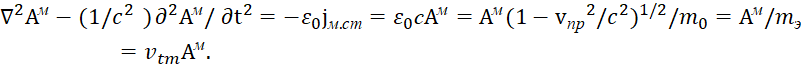 | (73) |
Данный вид уравнений совпадает с видом уравнения (68), полученным физиками, за исключением того, что уравнение (68) не может характеризовать реальные волновые процессы через пространственно-временное искривление с выполнением принципа Гюйгенса-Френеля в силу того, что значение ![]() . Иными словами, взаимодействие со средой распространения отсутствует. Однако не надо думать, что мы придумали нечто оригинальное, аналогичный вид с учётом взятия производной по времени был показан и в классической электродинамике в виде [31, с. 39-40]:
. Иными словами, взаимодействие со средой распространения отсутствует. Однако не надо думать, что мы придумали нечто оригинальное, аналогичный вид с учётом взятия производной по времени был показан и в классической электродинамике в виде [31, с. 39-40]:
| (74) |
Кроме того, в классической электродинамике показана связь векторных потенциалов с источниками возбуждения на основе электрических и магнитных составляющих в виде:
(75) |
Понятно, что в стационарном режиме в случае распада частиц можно сделать замену Е и Н на А и Ам в силу закона сохранения количества между противоположностями при взаимном обмене. То есть равный количественный обмен между противоположностями позволяет привести уравнения в зависимости от одной переменной. Для учёта волновых свойств от напряжённости электрического поля с учётом принципа Гюйгенса ‒ Френеля имеем:
(76) |
Для учёта волновых свойств от напряжённости магнитного поля с учётом принципа Гюйгенса ‒ Френеля имеем:
(77) |
Здесь мы учитываем, что напряжённости электрических и магнитных полей – это противоположности к векторным потенциалам, что определяется умножением на мнимую единицу. Напомним, что такой переход впервые ввели не мы, а это было сделано в квантовой механике в виде x4=ict или iФ=А4 [14, с. 317]. Кроме того, в силу противодействия электрической составляющей к магнитной составляющей, мы должны при переходе к общей системе наблюдения сделать замену знаков, так как законы физики, связанные с количественными изменениями, не могут иметь двузначный вид для одной общей переменной. Разница может касаться только представления объектов в статике в зависимости от принадлежности к противоположностям, что показано ниже. Собственно, в предпоследнем уравнении в (76) смену знака перед значением ротора (![]() ) с минуса на плюс можно рассматривать как смену действия на противодействие, или как смену переменных по координатам длины, так как иное в противоположных системах наблюдения означает отсутствие преобразований с влиянием противоположностей друг на друга. Таким образом, мы получаем два уравнения относительно одной переменной Ам в виде:
) с минуса на плюс можно рассматривать как смену действия на противодействие, или как смену переменных по координатам длины, так как иное в противоположных системах наблюдения означает отсутствие преобразований с влиянием противоположностей друг на друга. Таким образом, мы получаем два уравнения относительно одной переменной Ам в виде:
(78) |
Повторим, что, так как объекты сохраняются, то вместо электрических и магнитных сторонних токов можно ввести векторные потенциалы, исходя из идентичности законов в противоположностях. Здесь учитывается, что если для формирования магнитного или электрического волнового процесса в нашей системе наблюдения требовалась динамика изменения электрических и магнитных сторонних токов (67), то в противоположной системе наблюдения уже сам сторонний электрический или магнитный ток с учётом (73) выступает источником формирования волновых процессов в противоположности. В силу симметрии законов Мироздания в противоположностях для соблюдения закона сохранения количества это правило распространяется и на векторные потенциалы, а также электромагнитные составляющие.
Таким образом, мы выразили уравнения через векторные потенциалы, с учётом, что, ![]() и
и ![]() . Иными словами, мы учитываем, что векторный потенциал по координате длины отличается от векторного потенциала по координате времени на величину, связанную с усреднённой интегральной кинетической энергией в противоположности, выраженной через значение скорости
. Иными словами, мы учитываем, что векторный потенциал по координате длины отличается от векторного потенциала по координате времени на величину, связанную с усреднённой интегральной кинетической энергией в противоположности, выраженной через значение скорости ![]() по уравнению вида:
по уравнению вида: ![]() в соответствии с ОТО Эйнштейна. Здесь аналог для магнитных составляющих
в соответствии с ОТО Эйнштейна. Здесь аналог для магнитных составляющих ![]() , и аналог для электрических составляющих
, и аналог для электрических составляющих ![]() . Если исходить из известных законов физики, то в уравнениях (77) значение
. Если исходить из известных законов физики, то в уравнениях (77) значение ![]() выражает закон Фарадея, а уравнение
выражает закон Фарадея, а уравнение ![]() соответствует поглощению или излучению в окружающей среде. Однако с точки зрения нашей теории и с целью исключения парадоксов замкнутая система ротора определяет объект в виде константы в противоположности
соответствует поглощению или излучению в окружающей среде. Однако с точки зрения нашей теории и с целью исключения парадоксов замкнутая система ротора определяет объект в виде константы в противоположности ![]() , а оставшаяся часть определяет динамику изменения между противоположностями в пространстве и времени в виде
, а оставшаяся часть определяет динамику изменения между противоположностями в пространстве и времени в виде ![]() (уравнение непрерывности) в соответствии с СТО и ОТО Эйнштейна. Действительно, если допустить, что изменения по времени не приводят к изменениям по длине в соответствии с СТО и ОТО Эйнштейна, то тем самым исключается связь противоположностей и парадоксы с чудесами неизбежны.
(уравнение непрерывности) в соответствии с СТО и ОТО Эйнштейна. Действительно, если допустить, что изменения по времени не приводят к изменениям по длине в соответствии с СТО и ОТО Эйнштейна, то тем самым исключается связь противоположностей и парадоксы с чудесами неизбежны.
Если расписать систему уравнений (77) относительно приравнивания к нулю, и с учётом m0=1/c, а также, что ![]() , то мы получим:
, то мы получим:
(79) |
С учётом умножения на мнимую единицу будем иметь:
(80) |
В соответствии с системой Дирака (20), мы должны представить уравнения (80) в частных производных в зависимости аргумента функций по соответствующим переменным в виде:
(81) |
Понятно, что волновая функция Ам в каждом случае соответствующих производных по координатам длины и времени должна соответствовать волновым функциям Ψ по условию закона сохранения количества при преобразованиях. Действительно видно, что первое уравнение в (81) соответствует волновой функции Ψ2, с соответствующими производными по частям во втором, третьем, и четвёртом уравнениях системы Дирака (20). Разница между функциями только в том, что вместо значения в скорость света (с), присутствует величина (u=(c2–vпр2)1/2). И это разница связана с тем, что в системе уравнений Дирака на основе волновых функций, характеризующих вероятность, не учитывается состояние окружающей среды, в отличие от электромагнитных функций. Кроме того, при учёте влияния функции Ψ1 в системе уравнений Дирака, мы должны рассматривать условие смены системы наблюдения на противоположную систему, при котором сумма сменяется на разность, и наоборот. Иными словами, в своей системе уравнений Дирак использовал взаимодействие противоположностей с учётом рассмотрения от соответствующих систем наблюдения при переходе от волновых свойств к корпускулярным свойствам с учётом движения и смены знаков. Таким образом, мы при переходе от Ψ функций к реальным электромагнитным функциям через векторные потенциалы будем использовать те же условия взаимодействия, что применил Дирак. Иными словами, Дирак тоже не обошёлся без представления объектов в зависимости от системы наблюдения. Соответственно замену волновых функций Ψ на векторные потенциалы можно представить в виде:
(82) |
При этом волновые функции Ψ Луи де Бройля при соответствии уравнению энергии Эйнштейна имеют вид:
![]() , (83)
, (83)
Далее мы можем расписать уравнения на основе векторных потенциалов аналогично системе уравнений Дирака (20) с учётом (82) в виде:
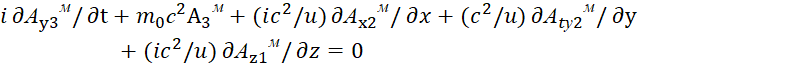 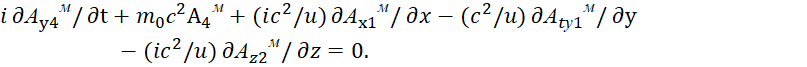 | (84) |
Здесь мы учитываем, что взаимодействие компонент векторных потенциалов при преобразовании и переходе от волновых свойств к корпускулярным свойствам меняется, так как иное означало отсутствие самого взаимодействия. После взятия производных по волновым функциям аналогичным (80) получим вид по аналогии с (18):
(85) |
С учётом выражения одних функций через другие для свободной частицы без внешнего электромагнитного поля получаем:
(86) |
Далее подставляем одни функции вместо других и сокращаем подобные члены:
(87) |
С учётом сокращения на общую волновую функцию ![]() , имеем энергию в квадрате для частиц с учётом кинетической энергии от противоположности. Для отражения движения без наличия внешних сил, как положительных (позитрон), так и отрицательных (электрон) частиц, имеем формулу энергии Эйнштейна:
, имеем энергию в квадрате для частиц с учётом кинетической энергии от противоположности. Для отражения движения без наличия внешних сил, как положительных (позитрон), так и отрицательных (электрон) частиц, имеем формулу энергии Эйнштейна:
![]() , (88)
, (88)
Таким образом, мы получили переход от волновых свойств к корпускулярным свойствам на основе векторного потенциала Ам, а это означает однозначную связь электромагнитных свойств с корпускулярными свойствами. В итоге уравнение (88) соответствует так называемым заряженным элементарным частицам (электрон, позитрон), которые отражают реально движение наипростейших объектов длины или времени, что мы показали в [32, с. 5-44; 33, с. 32-56].
Надо отметить, что уравнения (73) отражают формирование излучения на основе пространственно-временного искривления среды, что мы показали в [1, с. 7-38]. То есть, здесь отражено не влияние движения одной частицы от противоположности, а влияние от движения всех частиц от противоположности. При этом максимум кривой излучения по уравнению Планка соответствует стабильному состоянию таких частиц как электрон и протон. Так как представление электрических и магнитных составляющих зависит от скорости движения частиц и имеет место относительность магнитных и электрических полей [34, с. 269], то в этом случае должна быть связь между напряжённостями электрической и магнитной составляющими как противоположностей при подчинении СТО и ОТО Эйнштейна. Физики попытались показать эту связь по формуле, которая аналогична формуле связи длины и времени в виде:
| (89) |
В итоге Фейнман получил выражение [35, с. 269]:
![]() , (90)
, (90)
Сравнивая нижнее уравнение (89) с уравнением (90), мы видим отличие (90) от нижнего уравнения (89) в том, что в уравнение (90) входит константа магнитной проницаемости ![]() , которая характеризует состояние среды распространения. Соответственно есть разница и на величину
, которая характеризует состояние среды распространения. Соответственно есть разница и на величину ![]() . Отсюда можно сделать следующие преобразования формулы (90):
. Отсюда можно сделать следующие преобразования формулы (90):
(91) |
Последнее уравнение в (91) соответствует замкнутой системе двух противоположностей по уравнению окружности с учётом обратно-пропорциональной связи. Напомним, что с учётом нашей теории для элементарной частицы с массой m0=1/c, исходя из формулы Луи де Бройля, мы можем связать частоту и скорость в виде:
(92) |
Здесь необходимо отметить, что представление через частоту и скорость относится к противоположным системам наблюдения, связанным через скорость света. Иными словами, мы имеем первоначальную связь через скорость света аналогично связи длины и времени по идее Минковского [12, с. 226]. Из формулы (90) также следует, что представление процесса и физических величин также зависит от системы наблюдения. Теперь вспомним известную формулу Луи де Бройля для описания «волн материи» по которой со всякой неподвижной частицей массой m связан некоторый периодический процесс частоты f [6, с. 216-217] и учтём ОТО Эйнштейна, а также что по нашей теории m0=1/c=h:
(93) |
Это совпадает с результатом в (91). Иными словами, мы получаем один и тот же закон, что означает симметрию в противоположностях, и соответствует представлению электромагнитных составляющих в одной системе наблюдения как величин длины (массы) и времени (обратно-пропорциональна частоте) в противоположной системе наблюдения. Надо отметить, что формула (90) может рассматриваться как вклад в электромагнитное излучение в одной противоположности за счёт движения частицы в другой противоположности. Действительно, мы можем представить наличие магнитной индукции частицы с учётом движения в системе СИ в виде произведения:
![]() , (94)
, (94)
Собственно эта формула является обратной к формуле (91) [35, с. 89-269], при скорости v=c, но за счёт нормировки на скорость света мы имеем рассмотрение из противоположной системы наблюдения. Это по виду соответствует второму уравнению в (89) если считать ![]() , а
, а ![]() . Понятно, что при
. Понятно, что при ![]() , мы получаем в системе МКСА:
, мы получаем в системе МКСА:
![]() , (95)
, (95)
Иными словами, баланс между значениями констант электрической и магнитной проницаемости с точки зрения интегральных значений скоростей частиц в противоположностях соответствует начальному условию связи электрической и магнитной напряжённости поля в виде Н=сЕ. При этом скорость движения частицы v в одной противоположности связана с компенсацией движения в другой противоположности. Напомним, что такая же начальная связь была предложена Минковским [12, с. 226] r=ct, для таких противоположностей как длина и время.
Однако, как известно, электрон и позитрон, как противоположности, аннигилируют с превращением в фотоны. Отсюда их существование было бы невозможно, если бы в соответствии с нашей теорией между глобальными противоположностями не существовало закона, при котором кинетическая энергия в одной противоположности выглядит как потенциальная энергия в другой противоположности. И именно разница масс между протоном и электроном, с разным представлением кинетической и потенциальной энергии от систем наблюдения в противоположностях, исключает аннигиляцию. В соответствии с этим формула для энергии частицы физиками представлена в виде [36, с. 237]:
![]() , (96)
, (96)
Понятно, что изменение массы в (93) связано с переходом в противоположность которое определяется на основе баланса между константами электрической и магнитной проницаемости. В этом случае волновая функция в одной противоположности, вида: ![]() которая обеспечивала соответствие корпускулярных свойств электрону и позитрону должна отличаться от волновой функции в другой противоположности в соответствии с константой проницаемости, которая характеризует кинетическую энергию среды в данном месте. В этом случае мы имеем пересчёт, например, на константу электрической проницаемости, так как в противном случае между противоположностями нет отличий, связанных с выполнением СТО и ОТО Эйнштейна. При этом влияние кинетической энергии от движения в противоположности должно применяться ко всему аргументу функции, так как мы рассматриваем одну систему наблюдения с переходом в другую противоположную систему наблюдения и их связь определяется СТО и ОТО Эйнштейна. Иное (при применении перехода за счёт движения в аргументе только к энергии или импульсу) даёт изменение между энергией и импульсом в зависимости от противоположности и системы наблюдения. Это даёт скачок (разрыв) в выполнении законов физики при переходе, что противоречит симметрии и инвариантности, за счёт количественного различия между кинетической и потенциальной энергией. То есть не соблюдается закон сохранения количества при обмене между противоположностями. Отсюда мы будем иметь выражение функций в виде:
которая обеспечивала соответствие корпускулярных свойств электрону и позитрону должна отличаться от волновой функции в другой противоположности в соответствии с константой проницаемости, которая характеризует кинетическую энергию среды в данном месте. В этом случае мы имеем пересчёт, например, на константу электрической проницаемости, так как в противном случае между противоположностями нет отличий, связанных с выполнением СТО и ОТО Эйнштейна. При этом влияние кинетической энергии от движения в противоположности должно применяться ко всему аргументу функции, так как мы рассматриваем одну систему наблюдения с переходом в другую противоположную систему наблюдения и их связь определяется СТО и ОТО Эйнштейна. Иное (при применении перехода за счёт движения в аргументе только к энергии или импульсу) даёт изменение между энергией и импульсом в зависимости от противоположности и системы наблюдения. Это даёт скачок (разрыв) в выполнении законов физики при переходе, что противоречит симметрии и инвариантности, за счёт количественного различия между кинетической и потенциальной энергией. То есть не соблюдается закон сохранения количества при обмене между противоположностями. Отсюда мы будем иметь выражение функций в виде:
(97) |
В этом случае уравнение (84) c учётом операции дифференцирования по волновым функциям может быть представлено в виде:
(98) |
При нормировке на константу электрической проницаемости имеем вид:
(99) |
Собственно, это означает, что элементы среды распространения в соответствующей системе наблюдения на основании СТО и ОТО Эйнштейна рассматриваются как корпускулярные объекты с превращением кинетической энергии в потенциальную энергию, и наоборот.
С учётом выражения одних функций через другие для свободной частицы без внешнего электромагнитного поля получаем:
(100) |
При учёте значения константы электрической проницаемости ![]() подставляем одни функции вместо других и сокращаем подобные члены:
подставляем одни функции вместо других и сокращаем подобные члены:
(101) |
Здесь ![]() . Сокращая на волновую функцию
. Сокращая на волновую функцию ![]() , получаем соответствие с выражением энергии (96). При этом надо учитывать, что константы электрической и магнитной проницаемости также имеют зависимость от местоположения в среде распространения, что определяет баланс между частицами и средой в плане синтеза и распада. Соответственно, мы видим, что в отличие от нашей теории, система уравнений Дирака, без учёта состояния среды распространения, не способна описать частицы с разной массой покоя.
, получаем соответствие с выражением энергии (96). При этом надо учитывать, что константы электрической и магнитной проницаемости также имеют зависимость от местоположения в среде распространения, что определяет баланс между частицами и средой в плане синтеза и распада. Соответственно, мы видим, что в отличие от нашей теории, система уравнений Дирака, без учёта состояния среды распространения, не способна описать частицы с разной массой покоя.
Исходя из системы уравнений Дирака с учётом наших усовершенствованных уравнений Максвелла видно, что излучение и поглощение определяется сменой компонент по направлению в самой системе уравнений, и соответственно при этом происходит изменение направления движения частиц. Понятно, что этот процесс на практике (46) связан с излучением и поглощением электронных и мюонных нейтрино (антинейтрино), а также с их взаимодействием с излучением и поглощением фотонов. При этом сам процесс изменения связан с балансом по электромагнитному излучению и поглощению между частицами и окружающей средой. Как мы показали выше, процесс электромагнитного излучения в соответствии с формулой Планка на основе пространственно-временного искривления среды распространения определяется по уравнениям в (73). Однако данные уравнения (73) рассматривают вариант общего интегрального движения корпускулярных частиц в противоположности с отображением излучения за счёт констант электрической и магнитной проницаемости. Для отображения излучения, связанного с конкретной частицей, мы должны иметь соответствие частоты излучения импульсу с выполнением закона Луи де Бройля (92). В этом случае излучение в одной противоположности должно характеризоваться через импульс в другой противоположности, что было нами показано в [1, с. 7-38]. Отсюда при переходе в систему наблюдения от векторного потенциала Ф=Ам с учётом (67) имеем для верхнего уравнения (73):
(102) |
Здесь мы учитываем, что верхнее уравнение в (102) относится к рассмотрению от системы наблюдения, связанной с векторным потенциалом Ам (от противоположности, характеризующей длину в СТО Эйнштейна). При этом в системе наблюдения от волновых свойств, при скорости движения волны со скоростью света, мы учитываем, что в соответствующей противоположной системе наблюдения Ам=сА, и мы имеем нижнее уравнение в (102), что совпадает с (89). Данный подход соответствует идее Луи де Бройля, где волновой процесс в одной противоположности однозначно связан с импульсом движения частицы в другой противоположности с учётом обмена между противоположностями со скоростью света. Это отличается от концепции физиков, где формирование электромагнитного поля связывают с неким электрическим зарядом, который не имеет энергии, так как не входит в уравнение энергии Эйнштейна, что было учтено Дираком (![]() ). Следовательно, если в случае отображения от системы наблюдения от векторного потенциала Ам мы имели зависимость формирования волнового процесса от константы магнитной проницаемости, выраженной через неподвижное пространственно-временное искривление в виде массы
). Следовательно, если в случае отображения от системы наблюдения от векторного потенциала Ам мы имели зависимость формирования волнового процесса от константы магнитной проницаемости, выраженной через неподвижное пространственно-временное искривление в виде массы ![]() , то при отображении через векторный потенциал А, мы имеем представление от системы, связанной с наблюдением от времени, в которой масса
, то при отображении через векторный потенциал А, мы имеем представление от системы, связанной с наблюдением от времени, в которой масса ![]() уже движется со скоростью
уже движется со скоростью ![]() . Отсюда сохранение вида объектов при переходе в противоположность, например, только с заменой длины на время, и наоборот, исключало бы возможность взаимодействия и различия объектов за счёт изменения. Действительно представление изменения окружающей среды в противоположностях путём превращения длины на время, и наоборот, даёт однородность без объектов. А это означает отсутствие взаимодействия. Для нижнего уравнения в (73) мы должны учесть, что масса и скорость в противоположностях меняются местами с учетом (10) при обратно-пропорциональной связи (r=m=1/v) и в этом случае мы имеем уравнение (70) в виде:
. Отсюда сохранение вида объектов при переходе в противоположность, например, только с заменой длины на время, и наоборот, исключало бы возможность взаимодействия и различия объектов за счёт изменения. Действительно представление изменения окружающей среды в противоположностях путём превращения длины на время, и наоборот, даёт однородность без объектов. А это означает отсутствие взаимодействия. Для нижнего уравнения в (73) мы должны учесть, что масса и скорость в противоположностях меняются местами с учетом (10) при обратно-пропорциональной связи (r=m=1/v) и в этом случае мы имеем уравнение (70) в виде:
![]() , (103)
, (103)
Отсюда получаем:
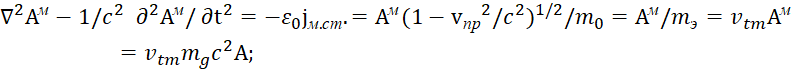 | (104) |
Здесь ![]() . Соответственно для нижнего уравнения в противоположной системе наблюдения, при Ам/с=А, таким образом, мы видим, что волновой процесс в одной системе наблюдения формируется за счёт корпускулярного движения в противоположной системе наблюдения, и наоборот. При этом скорость в одной системе наблюдения от А (кинетическая энергия) трансформируется в противоположной системе наблюдения от Ам в массу (потенциальная энергия), и наоборот. Фактически мы имеем закон, по которому движущийся электрон в одной системе наблюдения представляется протоном в другой системе наблюдения, за счёт смены скорости на массу, и данные представления частиц определяются на основе составляющих электромагнитной волны в соответствующей системе наблюдения. Не надо думать, что мы придумали в (102) и (104) нечто оригинальное. То есть, значение масс было введено в классическую электродинамику, но под видом плотности сторонних зарядов с подчинением СТО и ОТО Эйнштейна, как это было видно по уравнениям (40). Напомним, что по уравнению энергии Эйнштейна понятие заряда относится не к величине, а к знаку
. Соответственно для нижнего уравнения в противоположной системе наблюдения, при Ам/с=А, таким образом, мы видим, что волновой процесс в одной системе наблюдения формируется за счёт корпускулярного движения в противоположной системе наблюдения, и наоборот. При этом скорость в одной системе наблюдения от А (кинетическая энергия) трансформируется в противоположной системе наблюдения от Ам в массу (потенциальная энергия), и наоборот. Фактически мы имеем закон, по которому движущийся электрон в одной системе наблюдения представляется протоном в другой системе наблюдения, за счёт смены скорости на массу, и данные представления частиц определяются на основе составляющих электромагнитной волны в соответствующей системе наблюдения. Не надо думать, что мы придумали в (102) и (104) нечто оригинальное. То есть, значение масс было введено в классическую электродинамику, но под видом плотности сторонних зарядов с подчинением СТО и ОТО Эйнштейна, как это было видно по уравнениям (40). Напомним, что по уравнению энергии Эйнштейна понятие заряда относится не к величине, а к знаку ![]() , так как в формуле Эйнштейна заряд не обладает энергией. Следует ещё раз отметить, что, используя вектор – потенциалы, а также сторонние токи и заряды, физики до нас установили правило, по которому формирование волновых процессов в одной противоположности определяется движением объектов в другой противоположности. Отличие касается того, что они вопреки парадоксу
, так как в формуле Эйнштейна заряд не обладает энергией. Следует ещё раз отметить, что, используя вектор – потенциалы, а также сторонние токи и заряды, физики до нас установили правило, по которому формирование волновых процессов в одной противоположности определяется движением объектов в другой противоположности. Отличие касается того, что они вопреки парадоксу ![]() , ввели, как им казалось, полное значение плотности тока в уравнения Максвелла и получили:
, ввели, как им казалось, полное значение плотности тока в уравнения Максвелла и получили:
(105) |
Иными словами, если мы исходили из формирования объектов на основе усовершенствованных уравнений Максвелла, которые определяют реальные объекты в виде электронных и мюонных нейтрино (антинейтрино), то физики, пропустили цепочку образования движущихся объектов на основании взаимодействия электронных и мюонных нейтрино (антинейтрино) по системе уравнений Дирака. Собственно, это упрощение также привело их к наличию волновых свойств в противоположности через вектор – потенциалы в виде [37]:
| (106) |
При ![]() , а также
, а также ![]() , мы с учётом нашей теории при Ф=сА получаем, что эти два уравнения представляют собой вариант одного общего первого уравнения в (72):
, мы с учётом нашей теории при Ф=сА получаем, что эти два уравнения представляют собой вариант одного общего первого уравнения в (72):
![]() , (107)
, (107)
Однако следует отметить, что в этом случае мы имеем парадокс, отсутствия противоположностей в объекте, которые получались в нашем случае. Здесь, чтобы не нарушать принцип Гюйгенса-Френеля в каждой точке среды распространения должно быть взаимодействие распространяющегося электромагнитного поля с объектами среды, которые характеризуются как источники возбуждения. При этом в силу того, что мы имеем волновой вид как электрической, так и магнитной составляющей (а это противоположности), то эти источники возбуждения отличаются, но при возбуждении должны иметь изменяющийся во времени вид в данной точке возбуждения. И это отражено по формулам (73). Однако данный характер возбуждения это не наше новшество, фактически данный вид уравнений для излучения с источниками был получен и в классической электродинамике [38, с. 124-125] при попытке объяснить излучение электромагнитных полей через вибраторы Герца. В этом случае физики ввели поляризованность Р и намагниченность М в системе МКСА в виде:
(108) |
Иными словами, источниками волнового вида, в противоположной системе наблюдения, выступают напряжённости электрических и магнитных полей уже в нашей системе наблюдения с учётом пространственно-временного искривления среды распространения за вычетом начальных значений напряжённостей электромагнитных полей. Отсюда электрическая поляризованность и соответственно намагниченность в противоположности могут выступать как параметры длины и времени, характеризующие некий объект с подчинением ОТО Эйнштейна и при наличии инвариантности относительно систем координат. Данный вывод следует в силу того, что мы имеем одинаковое представление через уравнение окружности как для электромагнитных составляющих в (91), так и для формулы Луи де Бройля (93) вида ![]() . То есть, мы можем, исходя из симметрии, рассматривать эквивалентность формирования волновых процессов в противоположностях. При этом то, что рассматривается как длина и время характеризующая некий объект в одной противоположности отражается в виде силового воздействия электрических и магнитных составляющих в другой противоположности. Далее в классической электродинамике считают, что:
. То есть, мы можем, исходя из симметрии, рассматривать эквивалентность формирования волновых процессов в противоположностях. При этом то, что рассматривается как длина и время характеризующая некий объект в одной противоположности отражается в виде силового воздействия электрических и магнитных составляющих в другой противоположности. Далее в классической электродинамике считают, что:
(109) |
В таком случае электромагнитные потенциалы Ф и А могут быть найдены из уравнений:
(110) |
Следует отметить, что значения в первых двух уравнениях в (110), стоящие справа от знака равенства, не соответствуют (106) и (107) при ![]() , а также
, а также ![]() , так как в том случае предполагалась связь сА=Ф. Иными словами, выбран вариант формирования значения заряда и тока, без их взаимной связи через скорость света как противоположностей. При этом, если
, так как в том случае предполагалась связь сА=Ф. Иными словами, выбран вариант формирования значения заряда и тока, без их взаимной связи через скорость света как противоположностей. При этом, если ![]() , а
, а ![]() , то мы имеем идентичность уравнений. По сути, первое уравнение в (110) отражает формирование волновых процессов от пространственно-временного искривления среды в соответствии с идеей Луи де Бройля в статике, а вторая формула отражает волновой процесс от динамики изменения по обычному уравнению Максвелла. Это означает, что в данном случае волновые процессы по электродинамическим потенциалам формируются от противоположностей, при котором один волновой процесс по Ф связан с пространственно-временным искривлением по ОТО Эйнштейна, а второй волновой процесс по А связан с динамикой изменения с подчинением СТО Эйнштейна. Это подобно формируемым вкладам в (75) в классической электродинамике. Понятно, что волновые процессы от противоположностей должны обеспечивать баланс обмена между глобальными противоположностями (в силу закона сохранения количества), и таким образом, пространственно-временное искривление в одной противоположности (потенциальная энергия) формируется за счёт волновых процессов, связанных с кинетической энергией в другой противоположности, и наоборот. Иными словами, физики по (110) и без нас практически ввели разницу представления в зависимости от системы наблюдения от противоположности. Отсюда мы можем рассматривать правые части первого и второго уравнений в (110) как отражение формирования общего суммарного волнового электрического (или магнитного) процесса по компонентам поляризации и намагниченности, подобно сторонним токам по уравнениям (6). То есть, и в этом случае мы видим необходимость усовершенствования уравнений Максвелла для учёта отражения формирования суммарного волнового процесса по электрической или магнитной компоненте от противоположностей, так как проекции электромагнитных компонент на время характеризуют противоположность к компонентам по пространству.
, то мы имеем идентичность уравнений. По сути, первое уравнение в (110) отражает формирование волновых процессов от пространственно-временного искривления среды в соответствии с идеей Луи де Бройля в статике, а вторая формула отражает волновой процесс от динамики изменения по обычному уравнению Максвелла. Это означает, что в данном случае волновые процессы по электродинамическим потенциалам формируются от противоположностей, при котором один волновой процесс по Ф связан с пространственно-временным искривлением по ОТО Эйнштейна, а второй волновой процесс по А связан с динамикой изменения с подчинением СТО Эйнштейна. Это подобно формируемым вкладам в (75) в классической электродинамике. Понятно, что волновые процессы от противоположностей должны обеспечивать баланс обмена между глобальными противоположностями (в силу закона сохранения количества), и таким образом, пространственно-временное искривление в одной противоположности (потенциальная энергия) формируется за счёт волновых процессов, связанных с кинетической энергией в другой противоположности, и наоборот. Иными словами, физики по (110) и без нас практически ввели разницу представления в зависимости от системы наблюдения от противоположности. Отсюда мы можем рассматривать правые части первого и второго уравнений в (110) как отражение формирования общего суммарного волнового электрического (или магнитного) процесса по компонентам поляризации и намагниченности, подобно сторонним токам по уравнениям (6). То есть, и в этом случае мы видим необходимость усовершенствования уравнений Максвелла для учёта отражения формирования суммарного волнового процесса по электрической или магнитной компоненте от противоположностей, так как проекции электромагнитных компонент на время характеризуют противоположность к компонентам по пространству.
Далее, чтобы выполнить условие Лоренца, физики ввели так называемые электрический (П) и магнитный (Z) векторы Герца, сделав подстановку:
(111) |
Тогда верхнее уравнение (110) приводится к следующему виду:
(112) |
На следующем шаге учитывают, что одинаковые изменения по дивергенции не влияют на закон сохранения количества, и отсюда получают:
![]() , (113)
, (113)
Второе уравнение в (110) с учётом второго уравнения в (111) приводится к виду:
 | (114) |
Из уравнения (113) следует, что:
![]() , (115)
, (115)
Здесь а – произвольный вектор. Тогда первое уравнение из (111) сводится к следующему виду:
![]() , (116)
, (116)
Из него в свою очередь вытекает, что:
![]() , (117)
, (117)
Здесь ![]() – также произвольный скаляр.
– также произвольный скаляр.
Так как при изменениях в дифференциальном виде подстановка ![]() , и
, и ![]() не меняет зависимости от источников p и j, то в системе МКСА имеем:
не меняет зависимости от источников p и j, то в системе МКСА имеем:
(118) |
При выражении через напряжённости электрических и магнитных полей мы имеем:
(119) |
Собственно, мы получили аналог уравнений (73) при соответствующей замене переменных. Отсюда следует, что формируемая напряжённость в одной противоположности означает волновой процесс в другой противоположности.
При этом из классической электродинамики [38, с. 124-125] с учётом выражения электромагнитных составляющих через векторные потенциалы показано и обратное представление в виде:
(120) |
Собственно, нам непонятно, как был получен указанный результат, так как с учётом уравнений (111) мы получили следующий вид:
(121) |
Иными словами, значение ![]() во втором уравнении (121) было произвольно заменено на
во втором уравнении (121) было произвольно заменено на ![]() . И это было сделано с целью дальнейшей подгонки под результат при определении полей электрического и магнитного вибраторов Герца. Однако мы напомним, что, как было показано в [1, с. 7-38], исключить равенство нулю в математике выражения
. И это было сделано с целью дальнейшей подгонки под результат при определении полей электрического и магнитного вибраторов Герца. Однако мы напомним, что, как было показано в [1, с. 7-38], исключить равенство нулю в математике выражения ![]() , можно, только если рассматривать процесс с точки зрения изменений по пространству и времени, а не с учётом изменения только по пространству, где производные составляющие при вычитании идентичны. Поэтому все попытки при вычитании в динамике идентичных производных получить некоторое значение отличное от нуля равносильно чуду. Однако в случае обмена между противоположностями, какими являются длина и время, и при равенстве изменений по пространству и времени с соблюдением закона сохранения количества, мы не имеем противоречий. При этом, исходя из наличия представления П и Z, а также длины и времени, в виде закономерностей гиперболического косинуса и синуса по общей формуле Мироздания мы имеем уравнения волны с источником возбуждения. Собственно, только в этом случае замкнутый процесс в одной противоположности и системе наблюдения выражается в виде составляющей объекта в другой противоположности через воздействие. Соответственно тогда мы имеем равенство исходя из физики с заменой значения r=ct в соответствии с теорией Минковского [12, с. 226], что также фактически было сделано в электродинамике в первом уравнении (120), но для значения Z:
, можно, только если рассматривать процесс с точки зрения изменений по пространству и времени, а не с учётом изменения только по пространству, где производные составляющие при вычитании идентичны. Поэтому все попытки при вычитании в динамике идентичных производных получить некоторое значение отличное от нуля равносильно чуду. Однако в случае обмена между противоположностями, какими являются длина и время, и при равенстве изменений по пространству и времени с соблюдением закона сохранения количества, мы не имеем противоречий. При этом, исходя из наличия представления П и Z, а также длины и времени, в виде закономерностей гиперболического косинуса и синуса по общей формуле Мироздания мы имеем уравнения волны с источником возбуждения. Собственно, только в этом случае замкнутый процесс в одной противоположности и системе наблюдения выражается в виде составляющей объекта в другой противоположности через воздействие. Соответственно тогда мы имеем равенство исходя из физики с заменой значения r=ct в соответствии с теорией Минковского [12, с. 226], что также фактически было сделано в электродинамике в первом уравнении (120), но для значения Z:
![]() , (122)
, (122)
Фактически мы поменяли систему наблюдения на противоположную систему. Одновременно в соответствии с r=ct мы имеем такую же замену, связанную с переходом в противоположность и для второго члена справа от знака равенства в (121) ![]() и
и ![]() . Собственно, и эта замена не наше новшество, так как мы из классической электродинамики имеем, что при замене переменных дифференцирования с длины на время, и наоборот. в одном случае имеем:
. Собственно, и эта замена не наше новшество, так как мы из классической электродинамики имеем, что при замене переменных дифференцирования с длины на время, и наоборот. в одном случае имеем: ![]() , а в другом случае:
, а в другом случае: ![]() . То есть в первом случае производные выступают как единое целое, а во втором случае как противоположности. Иными словами, разомкнутость в одной противоположности означает замкнутость в другой противоположности с обнулением в динамике взаимодействия. Отсюда получаем обратный вид уравнений для напряжённостей полей от волновых процессов в виде:
. То есть в первом случае производные выступают как единое целое, а во втором случае как противоположности. Иными словами, разомкнутость в одной противоположности означает замкнутость в другой противоположности с обнулением в динамике взаимодействия. Отсюда получаем обратный вид уравнений для напряжённостей полей от волновых процессов в виде:
(123) |
Это противоречит уравнениям в (118) и означает, что мы имеем неоднозначность в представлении электрического (П) и магнитного (Z) векторов Герца, с одной стороны через электрическую поляризованность (P), и намагниченность (М), а с другой стороны через электрическую напряжённость Е и магнитную индукцию В. Исключить неоднозначность можно, если Р=Е, а М=В.
Понятно, что вид (122) с заменой волнового вида с изменением по пространству и времени на изменения только по пространству, также фактически был введён в электродинамике до нас, но с подгонкой под результат. Это было сделано для определения поля электрического вибратора Герца, длина которого l постоянна, а заряд отдельного полюса меняется со временем. Если рассматривать поле вибратора на расстоянии r>>l. , то его можно считать сосредоточенным диполем и положить ![]() , здесь
, здесь ![]() – дельта-функция. При определении полей электрического и магнитного вибраторов Герца [38, с. 124-125] считается, М=0, и вне вибратора Р=0. Но, если считать правильным (120), то это бы означало, что в (118) мы имеем плоские волны без взаимосвязи электромагнитных составляющих, и которые не подчиняются принципу Гюйгенса Френеля, так как Р=М=0. И это первая подгонка под результат. Соответственно физики предполагают, что векторы Герца имеют вид:
– дельта-функция. При определении полей электрического и магнитного вибраторов Герца [38, с. 124-125] считается, М=0, и вне вибратора Р=0. Но, если считать правильным (120), то это бы означало, что в (118) мы имеем плоские волны без взаимосвязи электромагнитных составляющих, и которые не подчиняются принципу Гюйгенса Френеля, так как Р=М=0. И это первая подгонка под результат. Соответственно физики предполагают, что векторы Герца имеют вид:
![]() , (124)
, (124)
При этом по (120), физики имеют уравнения:
![]() , (125)
, (125)
Заметим, что получить излучение, не имея перехода к волновому виду только на основании изменений по пространству невозможно. Далее используется уравнение:
![]() , (126)
, (126)
Однако надо отметить, что в данном варианте изменений по ротору величина ![]() , и соответствует радиусу. Поэтому при замкнутом процессе от ротора, она не может изменяться. Отсюда имеем:
, и соответствует радиусу. Поэтому при замкнутом процессе от ротора, она не может изменяться. Отсюда имеем:
![]() , (127)
, (127)
Но физики тем, что радиус окружности неизменен, пренебрегли, и получили:
![]() , (128)
, (128)
То есть мы имеем вторую подгонку под результат. Кроме того, величина любой замкнутой величины в динамике изменения производных по координатам должна равняться нулю, иначе это не ротор. То есть мы не имеем ротора как такового с равенством производных по координатам и это третья подгонка под результат. Отсюда следует, что дальнейшее определение электрических и магнитных полей электрического вибратора Герца по формулам (124–128) в классической электродинамике не имеет научной основы, и связывается с попыткой подгонки под результат.
Понятно, что такое обилие ссылок в нашей теории на уже известные уравнения в классической электродинамике и квантовой механике, а также учёт СТО и ОТО Эйнштейна уже давно должны были бы натолкнуть учёных на признание усовершенствованных уравнений Максвелла, тем более что они фактически описывают реальные объекты в виде электронных и мюонных нейтрино (антинейтрино). При этом вопрос стоял однозначно, либо чудеса волновых функций, характеризующих вероятность с телепортацией объектов, либо реальные волновые электромагнитные функции. Однако даже при отсутствии альтернативы, физики не хотят признавать то, что давно уже используется в электродинамике и квантовой механике.
Поэтому не признание усовершенствованных уравнений Максвелла касается не того, что мы что-то выдумали из головы на основании наших желаний, а того, что исходя из корыстных интересов и от некомпетентности, академики РАН РФ пытаются скрыть от студентов допущенные подгонки под результат, как в электродинамике, так и в квантовой механике. Однако в век информации это им вряд ли удастся сделать на продолжительное время. И чтобы не быть голословными в обвинениях мы приводим ответ из Администрации Президента РФ на рисунке 3.

Рис. 3. Ответ из Администрации Президента РФ
Надо отметить, что комиссия РАН РФ по борьбе с лженаукой также отмалчивается, как и все другие известные университеты (МГУ, МИФИ, МФТИ и т. д.), несмотря на наши неоднократные обращения. Можно было бы осуществить объективное обсуждение на конференциях, в средствах массовой информации или научных советах, так как существует венчурный инвестиционный фонд «Imperious Group», который должен по декларируемой своей деятельности способствовать продвижению изобретений и открытий. Однако и тут страх экспертов от неполноты знаний и компетентности не даёт возможности открыто обсудить проблемы и кризис в науке (рис. 4).
Рис. 4. Ответ от «Imperious Group»
Исходя из того, что эксперты внимательно ознакомились с материалами, следует вывод о том, что они не могли не заметить, что основной вопрос касается замены нереальных вероятностных волновых величин на реальные электромагнитные величины. А раз они не хотят продолжать сотрудничество, то это означает, что их устраивают чудеса в физике через телепортацию. В этой ситуации для борьбы с мракобесием в физике могут помочь только публикации наших статей в журналах.
.png&w=384&q=75)
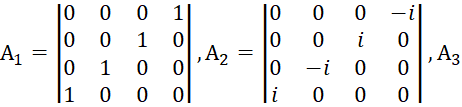
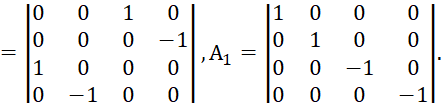
.png&w=640&q=75)