Введение
В данной статье рассматривается задача построения оптимальных одноимпульсных траекторий перелета с орбиты Луны в атмосферу Земли космического аппарата (КА) на основе принципа максимума с численным решением краевых задач методом стрельбы в рамках ограниченной круговой задачи трех тел. Рассматриваются перелеты в плоскости орбиты Луны с минимальными затратами характеристической скорости при ограниченном отрезке времени перелета.
Оптимизация траекторий играет важную роль в космических миссиях, так как позволяет снизить расход топлива и увеличить полезную нагрузку. В данной работе применяются современные методы численного моделирования, включая методы интегрирования дифференциальных уравнений и решения краевых задач.
Новизна данной работы заключается в применении численного метода стрельбы в сочетании с алгоритмами оптимизации для построения одноимпульсных траекторий возврата КА с орбиты Луны в атмосферу Земли. В отличие от классических методов, предложенный подход позволяет учитывать широкий диапазон начальных условий и минимизировать характеристики скорости, что повышает эффективность миссий с ограниченными запасами топлива.
Материалы и методы
Для моделирования движения космического аппарата (КА) использовалась ограниченная круговая задача трёх тел [4], где учитывается влияние гравитационных сил Земли и Луны, но пренебрегается воздействием КА на эти тела. Движение КА в этой системе описывается системой дифференциальных уравнений [4]:
| (1) |
Здесь ![]() – величина угловой скорости вращения системы Земля-Луна:
– величина угловой скорости вращения системы Земля-Луна:
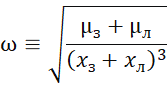 , (2)
, (2)
![]() – гравитационные параметры Земли и Луны,
– гравитационные параметры Земли и Луны, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – гравитационные ускорения у поверхностей Земли и Луны,
– гравитационные ускорения у поверхностей Земли и Луны, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – средние радиусы Земли и Луны,
– средние радиусы Земли и Луны, ![]() = 6378 км,
= 6378 км, ![]() = 1738 км,
= 1738 км, ![]() – расстояние между Землей и КА,
– расстояние между Землей и КА, ![]() – расстояние между Луной и КА:
– расстояние между Луной и КА:
![]() , (3)
, (3)
![]() ,
, ![]() ,
, ![]() ,
, ![]() – декартовы координаты и соответствующие им составляющие скорости центра масс КА,
– декартовы координаты и соответствующие им составляющие скорости центра масс КА, ![]() ,
, ![]() – координаты центра масс Земли и Луны:
– координаты центра масс Земли и Луны:
![]() , (4)
, (4)
![]() = 384400 км – расстояние между Землей и Луной.
= 384400 км – расстояние между Землей и Луной.
На траектории активное управление отсутствует (осуществляется импульсное воздействие в начальный момент времени), ![]() ,
, ![]() ,
, ![]() ,
, ![]() – кусочно-гладкие функции, удовлетворяющие уравнениям выше.
– кусочно-гладкие функции, удовлетворяющие уравнениям выше.
В итоге рассматриваемая задача оптимизации формализуется в следующем виде:
| (5) |
Где I – функционал, представляющий собой квадрат величины импульсного воздействия в начальный момент времени, – скорость на траектории ухода после импульсного воздействия:
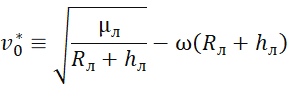 , (6)
, (6)
![]() – краевые условия,
– краевые условия, ![]() – конечный момент времени (T = 250000 с).
– конечный момент времени (T = 250000 с).
Данная задача решается на основе принципа Лагранжа снятия ограничений в импульсной постановке [2].
Для решения задачи применялись численные методы:
- Метод стрельбы [1, 5] для численного решения краевой задачи;
- Метод Дормана-Принса 8 (7) [6] для интегрирования системы дифференциальных уравнений;
- Метод Ньютона в модификации Федоренко [5] с нормировкой Исаева-Сонина [3, с. 1114-1116] для решения нелинейных систем уравнений.
Результаты
В ходе расчетов были определены оптимальные параметры одноимпульсного перелета, включая начальные скорости и углы выхода с орбиты Луны.
Рассчитанные параметры:
- Угол схода с орбиты Луны: 0,196°.
- Угол входа в атмосферу Земли: 0,0828°.
- Оптимальные значения скоростей на различных этапах перелета.
Дополнительно был проведен анализ влияния начальных условий на траекторию КА, включая варьирование начального импульса и времени запуска.
Построенная траектория удовлетворяет всем ограничениям краевой задачи с точностью, равной ![]() (рис. 1).
(рис. 1).
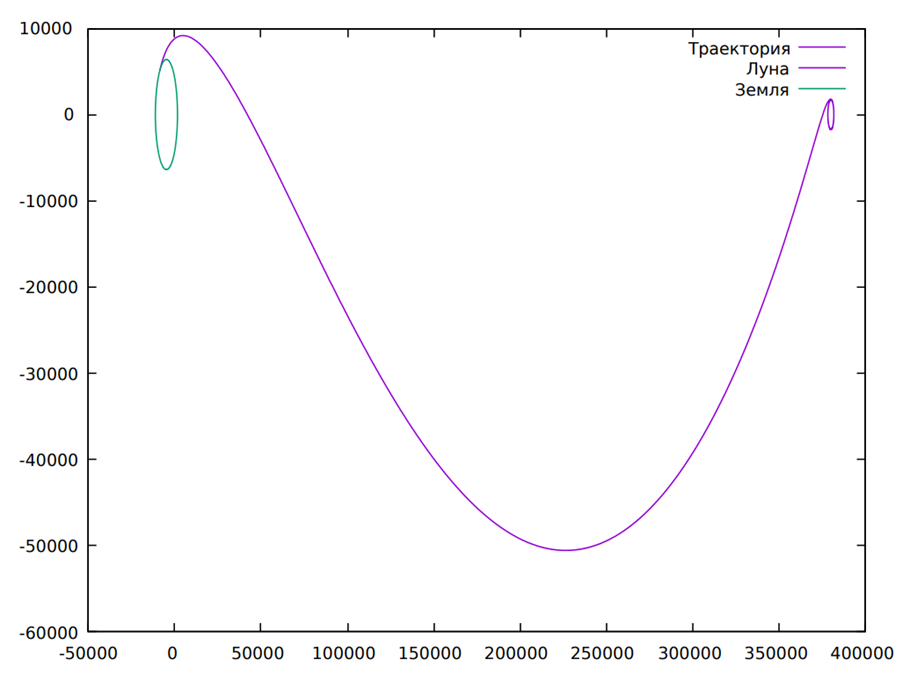
Рис. 1. Траектория возврата КА
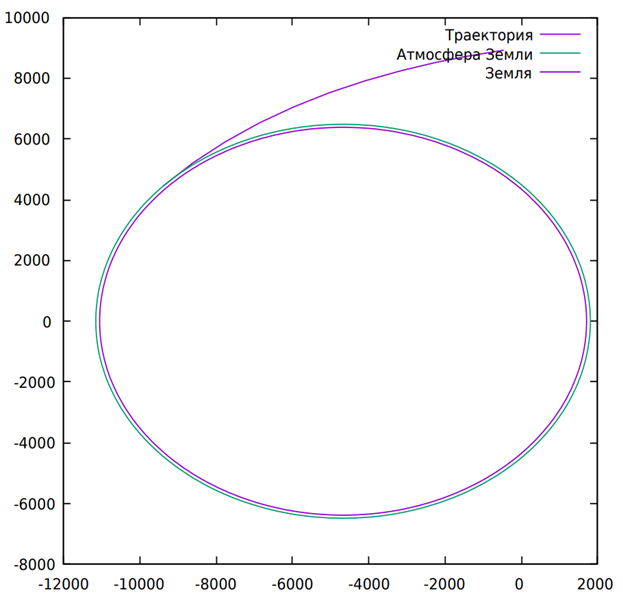
Рис. 2. Части на входе в атмосферу Земли траектории возврата КА
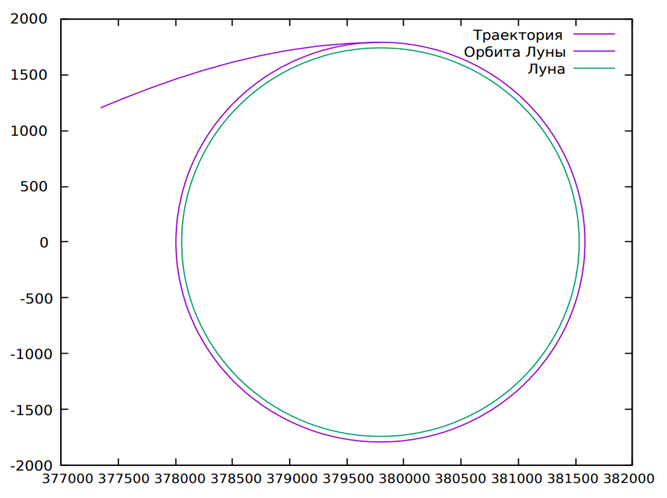
Рис. 3. Части на сходе с орбиты Луны траектории возврата КА
Заключение
В данной работе была рассмотрена задача оптимизации одноимпульсных траекторий возврата с орбиты ИСЛ. Задача была формализована в соответствии с методикой [2]. На основе соответствующего принципа Лагранжа её решение свелось к решению краевой задачи импульсной постановки. Краевая задача решена численно методом стрельбы. Входящая в метод стрельбы задача Коши для системы ОДУ решалась численно методом Дормана-Принса 8 (7), система нелинейных уравнений для вектор-функции невязок – методом Ньютона-Исаева-Сонина, система линейных алгебраических уравнений – методом Гаусса с выбором ведущего элемента по столбцу, производные вычислялись с использованием конечных разностей. В результате решения задачи определена экстремаль.
.png&w=384&q=75)
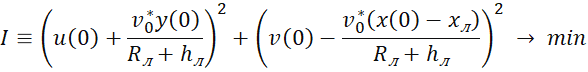
.png&w=640&q=75)