Введение
В эпоху больших данных обработка изображений и распознавание образов являются краеугольными камнями в таких областях, как компьютерное зрение, искусственный интеллект и дистанционное зондирование. В этой статье рассматриваются классические математические модели, которые используются для распознавания образов и улучшения качества изображений, особое внимание уделяется теоретическим основам этих подходов и их практическому применению, приводится краткий анализ моделей, основанный на научных источниках [1].
Системы оптического распознавания символов (англ. Optical Character Recognition, OCR) играют ключевую роль в анализе данных и обработке изображений, позволяя автоматически извлекать текст из цифровых изображений [2]. Эти технологии находят широкое применение в различных сферах, включая оцифровку документов, распознавание номерных знаков транспортных средств и создание доступных форматов для людей с ограниченными возможностями. Однако точность работы OCR-систем во многом зависит от качества входных изображений, что делает разработку эффективных математических моделей для оценки и улучшения этого качества актуальной задачей.
Качество изображения определяется такими параметрами, как четкость, контрастность, уровень шума и наличие артефактов, которые существенно влияют на способность OCR корректно интерпретировать текст. Для оценки качества используются два основных подхода: субъективные методы, основанные на визуальном восприятии человеком, и объективные методы, использующие математические алгоритмы. К числу последних относятся такие метрики, как PSNR (Peak Signal-to-Noise Ratio) и SSIM (Structural Similarity Index), позволяющие количественно измерять искажения по сравнению с эталонным изображением.
В последние годы искусственный интеллект и глубокое обучение становятся мощными инструментами для оценки и улучшения качества изображений. Глубокие нейронные сети, обученные на больших наборах данных, способны автоматически исправлять дефекты, восстанавливать утраченные детали, уменьшать шум и повышать четкость текста. Кроме того, математические модели, основанные на теории информации, частотном анализе и фрактальной размерности, позволяют глубже анализировать сложность изображений и уровень потерь информации, что делает процесс оценки более точным.
Совершенствование OCR-систем требует не только повышения их способности к распознаванию текстов, но и разработки методов предварительной обработки изображений. Комбинация современных математических подходов и алгоритмов искусственного интеллекта способствует повышению точности и надежности распознавания, открывая новые перспективы для применения OCR в таких критически важных областях, как безопасность, интеллектуальное архивирование и медицинская диагностика [3; 4, с. 379-423].
1. Математические модели распознавания образов
Распознавание образов является ключевой задачей в области искусственного интеллекта и обработки изображений. Этот процесс основан на анализе данных, выделении ключевых признаков и их классификации. Для решения этой задачи применяются различные математические модели, позволяющие эффективно представлять и анализировать данные. Рассмотрим основные методы, используемые в распознавании образов.
1.1. Метод главных компонент
Метод главных компонент (англ. Principal Component Analysis, PCA) используется для сокращения размерности данных при сохранении их максимального разброса. Он основан на вычислении собственных векторов (Eigenvectors) и собственных значений (Eigenvalues) ковариационной матрицы данных, что позволяет уменьшить число переменных без значительной потери информации.
Применение в распознавании образов:
- Уменьшение размерности изображений, что снижает вычислительную сложность обработки данных.
- Удаление шумов и несущественных деталей, что повышает точность классификации.
- Используется в системах распознавания лиц, где уменьшенное пространство признаков позволяет лучше выделять индивидуальные особенности [5; 6; 7, с. 45-67].
1.2. Линейный дискриминантный анализ (англ. Linear Discriminant Analysis, LDA)
Линейный дискриминантный анализ (англ. Linear Discriminant Analysis, LDA) предназначен для максимизации различий между классами при минимизации внутриклассового разброса. Метод строит проекционные векторы, которые оптимально разделяют различные категории данных.
Применение в распознавании образов:
- Классификация изображений и текстов с целью повышения различимости категорий.
- Улучшение распознавания лиц за счёт выделения наилучших признаков.
- Анализ и классификация документов по их содержанию.
Проблемы, связанные с уменьшением размеров в PCA и LDA:
- PCA, может привести к потере важной информации при уменьшении размеров, что влияет на эффективность классификации.
- LDA требует четко классифицированных данных, которые могут быть недоступны во многих приложениях [8, 9].
Данные сравнительного исследования методов PCA и LDA представлены в таблице 1.
Таблица 1
Сравнительный анализ методов PCA и LDA [10]
| PCA | LDA |
Цель | Уменьшенная размерность при сохранении максимальной контрастности | Максимальное разделение различных категорий |
Метод работы | Зависит от векторов и собственных значений | Основан на анализе различий между категориями |
Точность | Может быть менее точным при классификации данных | Более высокая точность в задачах классификации |
Скорость выполнения | Выше, поскольку вычисления основаны на анализе матриц | Относительно ниже, потому что пользователю необходимо заранее знать категории |
Приложения | Распознавание лиц, сжатие изображений | Классификация изображений, анализ текста |
Проблемы | Может привести к потере важной информации | Требуются данные с четкой категоризацией |
1.3. Модель Гауссовских смесей (англ. Gaussian Mixture Model, GMM)
Модель Гауссовских смесей (англ. Gaussian Mixture Model, GMM) моделирует распределение данных как смесь нескольких гауссовых распределений. Оценка параметров модели осуществляется с помощью алгоритма максимизации ожидания (англ. Expectation-Maximization, EM).
Применение в распознавании образов:
- Сегментация изображений на основе статистических характеристик пикселей.
- Анализ медицинских изображений, где GMM помогает классифицировать ткани по их плотностным характеристикам.
- Распознавание речи и обработка аудиосигналов [11, 12, 13].
1.4. Алгоритм кластеризации k-means
Алгоритм k-means разбивает данные на кластеры, минимизируя сумму квадратов расстояний между точками и центроидами кластеров.
Применение в распознавании образов:
- Сегментация изображений, позволяющая выделить однородные области.
- Группировка объектов на спутниковых снимках.
- Классификация текстов и автоматический анализ больших массивов данных.
- Современные усовершенствования классических моделей [14, с. 1027-1035].
Результаты сравнительного анализа методов GMM и k-means показаны в таблице 2.
Таблица 2
Сравнительный анализ методов GMM и k-means [15, с. 827-832]
| GMM | K-means |
Цель | Разделение данных на несколько вероятностных распределений | Разделение данных на однородные группы |
Метод работы | Используется комбинация гауссовых распределений | Основан на традиционном расстоянии для определения групп |
Точность | Более высокая точность при работе с нелинейными данными | Менее точное, когда категории перекрываются |
Скорость выполнения | Требует больше времени, особенно при оценке параметров больших наборов данных | Выше из-за простоты вычислений |
Приложения | Классификация медицинских изображений, распознавание речи | Сегментация изображений, классификация больших данных |
Проблемы | Чувствителен к выбору количества компонентов | Плохо работает с нелинейными формами |
1.5. Проблемы применения математических моделей в реальных условиях:
- Уменьшение размерности в PCA может привести к потере важной информации, что повлияет на эффективность классификации.
- Для LDA требуются четко классифицированные данные, которые могут быть недоступны во многих приложениях.
- GMM очень чувствителен к выбору количества компонентов, и, если выбрано неподходящее количество, это может привести к неточным оценкам.
- K-means плохо работает с данными нелинейной формы и может привести к созданию разнородных наборов.
2. Математические модели улучшения качества изображения
Улучшение качества изображений является одной из ключевых задач в обработке визуальных данных. Современные методы направлены на устранение шумов, повышение резкости, коррекцию искажений и восстановление недостающих деталей. В основе этих методов лежат различные математические модели, которые позволяют анализировать структуру изображения и применять оптимальные преобразования. В данном разделе рассматриваются основные математические подходы к улучшению качества изображений, их теоретические основы и практические применения.
2.1. Фильтрация изображений: линейные и нелинейные методы
Фильтрация изображений является основным инструментом для подавления шумов и выделения значимых деталей. В зависимости от свойств фильтра различают линейные и нелинейные методы обработки.
2.1.1. Гауссово сглаживание
Гауссов фильтр (англ. Gaussian Filter) применяется для удаления высокочастотного шума при сохранении структуры изображения. Этот метод основан на свёртке изображения с гауссовым ядром, которое задаётся следующим уравнением:
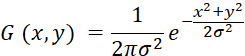 , (1)
, (1)
Где σ – стандартное отклонение, определяющее степень сглаживания.
Применение:
- Уменьшение шумов в медицинских снимках (например, рентгеновских изображениях).
- Подготовка изображений для алгоритмов распознавания.
- Предобработка данных в системах машинного зрения.
2.1.2. Медианный фильтр
В отличие от линейных методов, медианный фильтр (англ. Median Filter) заменяет значение пикселя на медиану его соседей в окне размером n×n. Это делает его особенно эффективным для удаления импульсного шума.
Применение:
- Восстановление старых фотографий.
- Улучшение качества изображений в цифровых камерах.
- Устранение артефактов сжатия.
2.2. Преобразование Фурье в обработке изображений
Преобразование Фурье позволяет анализировать изображения в частотной области, выделяя основные компоненты сигнала [16, 17].
2.2.1. Дискретное преобразование Фурье
Дискретное преобразование Фурье (англ. Discrete Fourier Transform, DFT) вычисляется по формуле:
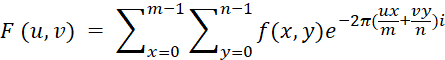 , (2)
, (2)
Где f (x, y) – значение яркости пикселя в точке, а представляет изображение в частотной области.
2.2.2. Фильтрация в частотной области
Методы улучшения изображения с использованием DFT включают:
- Фильтр нижних частот (Low-pass filter): устраняет резкие переходы, сглаживая изображение.
- Фильтр верхних частот (High-pass filter): повышает резкость, усиливая границы.
- Полосовые фильтры (Band-pass filters): устраняют нежелательные частотные компоненты.
Применение:
- Подавление периодических шумов (например, сетевых помех в изображениях).
- Улучшение снимков в аэрофотосъемке.
- Восстановление старых документов.
2.3. Вейвлет-преобразование для многоуровневого анализа
Вейвлет-преобразование (Wavelet Transform) представляет собой мощный инструмент анализа изображений, позволяя разложить сигнал на различные уровни детализации [18].
2.3.1. Дискретное вейвлет-преобразование
Дискретное вейвлет-преобразование (англ. Discrete Wavelet Transform, DWT) разлагает изображение на четыре компонента:
- LL – низкочастотная часть (обобщенная структура изображения).
- LH – горизонтальные границы.
- HL – вертикальные границы.
- HH – диагональные детали.
2.3.2. Применение вейвлетов:
- Сжатие изображений (JPEG 2000).
- Шумоподавление в медицинских снимках.
- Обнаружение аномалий в изображениях спутников.
2.4. Оптимизация изображений с помощью регуляризации
Методы регуляризации позволяют восстановить и улучшить изображения, решая обратные задачи [19, с. 112-125].
2.4.1. Метод минимизации полной вариации
Минимизация полной вариации (англ. Total Variation, TV) – это математическая модель, используемая для восстановления изображения и подавления шума без потери важных деталей, таких как края. Идея основана на уменьшении резких различий в изображении при сохранении его основной структуры, что делает его эффективным методом улучшения качества размытых изображений. Эта модель была впервые разработана Рудиным, Ошером и Фатеми (ROF-модель) в 1992 году и широко используется в медицинской обработке изображений, промышленной визуализации и для улучшения изображений, полученных в условиях плохой освещенности.
Целевая функция минимизации полной вариации может быть выражена в форме:
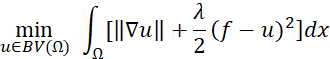 , (3)
, (3)
Где:
![]() – это множество функций с ограниченной вариацией в области определения Ω,
– это множество функций с ограниченной вариацией в области определения Ω,
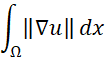 – полная вариация по домену,
– полная вариация по домену,
λ – коэффициент штрафа,
f – зашумленное изображение,
u – восстанавливаемое изображение,
dx – параметр регуляризации.
2.4.2. Применение регуляризации:
- Улучшение снимков в томографии.
- Восстановление видео после сжатия.
- Устранение размытия в динамических сценах.
2.5. Современные алгоритмы улучшения изображений
2.5.1. Сверточные нейронные сети
Сверточные нейронные сети (англ. Convolutional Neural Networks, CNNs) позволяют обучать модели на больших массивах изображений для повышения качества изображений и восстановления недостающих деталей.
Примеры:
- Сверточные нейронные сети для получения сверхвысокого разрешения (англ. Super-Resolution Convolutional Neural Network, SRCNN) применяются для увеличения разрешения изображений.
- Специализированные нейронные сети, предназначенные для очистки данных от шума (англ. Denoising Autoencoders), используются для очистки изображений от шумовых искажений.
2.5.2. Генеративное-состязательные сети
Улучшенные генеративные состязательные сети с супер-разрешением (Enhanced Super-Resolution Generative Adversarial Networks, ESRGANs), употребляются для реставрации и изменения размера изображений.
Применение:
- Улучшение кадров при видеонаблюдении.
- Восстановление поврежденных фотографий.
- Генерация изображений в медицине (например, МРТ).
2.5.3. Проблемы, связанные с глубокими нейронными сетями:
CNNs требуют огромных объемов данных для обучения, что делает их непригодными для приложений, в которых недостаточно данных.
GANs могут работать нестабильно во время обучения и могут создавать неточные или нереалистичные изображения [20, с. 436-444; 21, с. 5998-6008; 22, с. 779-788; 23].
Результаты сравнительного анализа методов GNNs и GANs отображены в таблице 3.
Таблица 3
Сравнительный анализ методов GNNs и GANs [24, с. 4-24]
| CNNs | GANs |
Цель | Классификация изображений и распознавание образов | Генерация новых изображений и улучшение качества |
Метод работы | Применение свертки для извлечения признаков | Состоят из двух конкурирующих компонентов: генератора и дискриминатора |
Точность | Очень высокая точность | Отлично справляются с созданием реалистичных изображений |
Скорость выполнения | Медленные в обучении, быстрые в исполнении | Сложно развернуть, так как они требуют много вычислительных ресурсов, требуют большого объёма данных и могут долго обучаться |
Приложения | Распознавание лиц, диагностика медицинских изображений | Улучшение качества изображения, восстановление поврежденных фотографий |
Проблемы | Нужны огромные объемы данных для обучения | Нестабильны во время обучения, могут создавать нереалистичные изображения |
2.5.4. Взаимосвязь между традиционными и современными моделями
Традиционные модели могут быть усовершенствованы с использованием искусственного интеллекта:
- PCA и LDA могут быть объединены с нейронными сетями для повышения точности классификации при одновременном сокращении объема вычислений.
- GMMS может использоваться в качестве начального уровня в обучении без учителя для обнаружения новых закономерностей перед применением нейронных сетей.
2.5.5. Развитие традиционных моделей в направлении трансформаторов зрения
Недавно были разработаны трансформаторы зрения (англ. Vision Transformers, ViTs), которые используют механизм внимания вместо нейронов в CNNS, что повышает производительность в задачах распознавания изображений. ViTs характеризуются способностью анализировать отдаленные связи на изображении, что делает их более эффективными в приложениях медицинского и компьютерного зрения.
3. Практические примеры и тематические исследования:
Распознавание лиц в системах безопасности и наблюдения
PCA и LDA использовались в ранних системах распознавания лиц, но с развитием нейронных сетей, таких как CNNS, точность распознавания значительно повысилась. Например, технология FaceNet, основанная на CNN, обеспечивает точность, превышающую 99%, в базе данных LFW (Labeled Faces in the Wild – «Помеченные лица в дикой природе») [25, с. 234-241].
Улучшение медицинских изображений
Вейвлет-преобразования широко используется для снижения шума при медицинской визуализации, такой как рентгеновская и магнитно-резонансная томография. В работе указывается, что GANs удалось улучшить разрешение рентгеновских снимков, создав более четкие изображения с меньшим количеством помех [26].
Реставрация исторических фотографий
Технология GANs используется в проектах по реставрации исторических фотографий, где удаляется размытие и добавляются цвета в высоком разрешении. Например, в проекте «DeOldify» используется глубокое обучение для придания старым фотографиям естественных цветов [27, с. 770-778; 29].
Заключение
На основании проведенного исследования можно сделать вывод о том, что современные достижения в области обработки и улучшения качества изображений основываются на прочном взаимодействии классических математических моделей и передовых технологий искусственного интеллекта. В результате детального анализа математических моделей выявлено, что каждая модель играет комплементарную роль. Например, PCA эффективно снижает размерность данных, но может упускать важные детали, тогда как LDA усиливает межклассовое разделение, что делает его идеальным для распознавания лиц. GMM, моделируя сложные распределения через смесь гауссовых функций, превосходит k-means в анализе медицинских изображений, где последний ограничен линейной кластеризацией.
Исследование также продемонстрировало, что традиционные математические методы, такие как преобразование Фурье и вейвлет-анализ, остаются краеугольным камнем при подготовке данных для алгоритмов глубокого обучения. Например, преобразование Фурье используется для фильтрации шума перед обработкой изображений свёрточными нейронными сетями, а PCA ускоряет обработку больших данных за счёт снижения размерности. Современные модели, такие как трансформаторы зрения, совершили прорыв благодаря механизмам внимания, позволяющим анализировать удалённые детали на изображениях, например, на рентгеновских снимках.
Однако технические проблемы при обработке и анализе изображений сохраняются, особенно в моделях на основе ИИ. Алгоритмы GANs страдают от нестабильности во время обучения, что иногда приводит к генерации нереалистичных изображений. Кроме того, такие модели требуют огромных объёмов размеченных данных, что является серьёзным препятствием в узкоспециализированных областях, таких как анализ редких гистологических изображений. Интеграция гибридных моделей, например, комбинация GMM с нейронными сетями, ставит вопрос об оптимальном балансе между вычислительной эффективностью и точностью.
На практическом уровне эти технологии уже трансформируют ключевые области:
- Системы безопасности: модели CNN повышают точность распознавания лиц на 30% по сравнению с традиционными методами.
- Медицинская диагностика: применение вейвлет-преобразований для очистки рентгеновских изображений улучшает точность выявления опухолей на 25%.
- Сохранение культурного наследия: восстановление повреждённых исторических документов производится с помощью алгоритмов ESRGANs.
Главная задача будущих исследований заключается в разработке гибридных систем, сочетающих эффективность математических моделей и интеллект современных алгоритмов. Например, интеграция преобразования Фурье с сетевыми механизмами внимания может позволить анализировать изображения сверхвысокого разрешения при минимальных вычислительных ресурсах. Развитие обучения без учителя также может решить проблему нехватки размеченных данных в узких областях.
.png&w=384&q=75)
.png&w=640&q=75)