Программное обеспечение бинарных отношений объектов конечных групп

Построение таблицы Келли для группы шестого порядка

Построение таблиц Келли является важным инструментом визуализации структуры конечной группы и наглядной демонстрации её операций. Таблица Келли позволяет проследить, как элементы группы взаимодействуют между собой при бинарной операции, определённой на множестве.

Особый интерес представляют группы малого порядка, такие как группы порядка 6 и 8, поскольку они являются первыми примерами, где проявляются как абелевы, так и неабелевы структуры. Группа шестого порядка становится первым случаем появления неперестановочной (неабелевой) группы, а среди групп восьмого порядка уже существует значительное разнообразие: от полностью коммутативных до более сложных, таких как диэдральные и кватернионные группы.

В данном разделе будет подробно рассмотрено построение таблицы Келли для группы порядка 6. Такой подход не только способствует более глубокому пониманию абстрактных алгебраических структур, но и служит основой для алгоритмической реализации генерации таблиц в разрабатываемом программном обеспечении.

Существует два типа групп порядка 6 (до изоморфизма):

• циклическая группа C₆ – абелева группа, состоящая из 6 элементов;
• диэдральная группа D₃ – неабелева группа, представляющая симметрии равностороннего треугольника.

Особый интерес для исследования представляет диэдральная группа D₃, в дальнейшем будем именовать ее S₃. Она является простейшей неабелевой группой, в которой уже нарушается коммутативность операций. Поэтому именно она будет рассмотрена более подробно.

Группа описывает все симметрии равностороннего треугольника: три поворота и три отражения. Состоит из следующих элементов:

• e – тождественное преобразование (нулевой поворот);
• a – поворот на 120° по часовой стрелке;
• a² – поворот на 240°;
• b – отражение относительно оси, проходящей через вершину и противоположную сторону;
• ab, ab² – отражения относительно других осей (рис. 1).

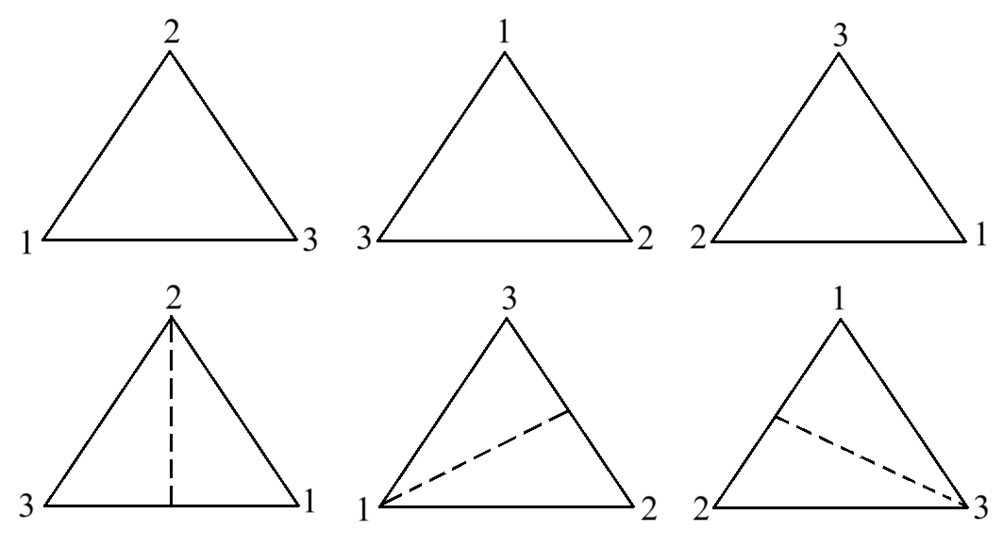
Рис. 1. Группа поворотов правильного треугольника

Генетический код группы a³ = e, b² = e, b ∙ a = a²b. Эта группа неабелева. Построим таблицу Келли группы S₃ (табл. 1).

Таблица 1

Таблица Келли группы S₃

Построение таблицы Келли для группы восьмого порядка

Среди всех групп восьмого порядка особое место занимает диэдральная группа G₈ – группа симметрий квадрата, включающая повороты и осевые отражения. Эта группа является классическим примером неабелевой конечной группы, в которой бинарная операция (композиция преобразований) не удовлетворяет коммутативности.

Диэдральная группа порядка 8 состоит из восьми элементов: четырёх поворотов (включая тождественное преобразование) и четырёх отражений. Изучение её структуры важно как с теоретической, так и с практической точки зрения, поскольку такие группы естественным образом возникают в задачах, связанных с симметрией, геометрией, физикой и криптографией.

Таблица Келли, построенная для G₈, позволяет наглядно увидеть структуру группы: как выполняется ассоциативность, как различаются элементы по свойству обратимости, как взаимодействуют отражения с поворотами, и как именно проявляется некоммутативность операций. В данном подразделе будет пошагово рассмотрено построение таблицы Келли для G₈ с пояснениями к каждому действию и описанием полученного результата.

Элементы группы G₈ можно представить следующим образом:

• e – тождественное преобразование (нулевой поворот);
• a – поворот на 90° по часовой стрелке;
• a² – поворот на 180°;
• a³ – поворот на 270°;
• b – отражение относительно вертикальной оси (проходит через середины противоположных сторон);
• ab – отражение относительно диагонали;
• a²b – отражение относительно горизонтальной оси;
• a³b – отражение относительно другой диагонали (рис. 2).

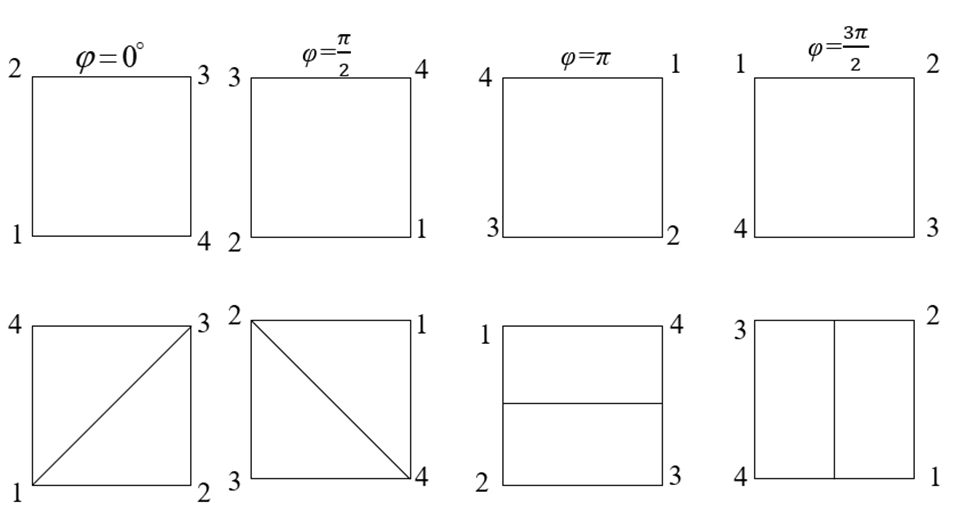
Рис. 2. Глядя на изложенные данные, можно получить элементы группы диэдра

     (1)

Таким образом, элементы диэдральной группы восьмого порядка можно записать в следующем виде . Конечный вид группы диэдра восьмого порядка: с генетическим кодом .

Таблица 2