Полиномы для описания упрочнения материалов

Для изучения пластических свойств материалов проводят механические испытания на растяжение круглых и плоских образцов из различных материалов [1, 2]. При этом получают кривую упрочнения материала и значение модуля упругости, предела текучести, предела прочности, относительного удлинение при разрыве и так далее [2, 3]. В марочниках сталей (материалов) кривую упрочнения не приводят, а только указывают числовые значения ряда основных механических характеристик - модуля упругости, предела текучести, предела прочности и так далее [3]. Однако при вычислении изгибающих моментов металлических образцов необходимо точно знать аналитическую зависимость кривой упрочнения (функцию напряжения от относительного удлинения). Для этого ниже даны аналитические описания кривой упрочнения с помощью квадратных и кубических полиномов. Рассматриваются случаи с тремя граничными условиями (квадратные полиномы) и четырьмя граничными условиями (кубические полиномы) при решении выше поставленной задачи.

Прямая параболическая аппроксимация (вариант 1). Будем считать, что кривая упрочнения проходит через предел текучести, предел прочности и имеет максимум в пределе прочности (в момент образования шейки образца). В этом случае аналитическое описание кривой упрочнения имеет вид

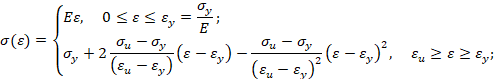
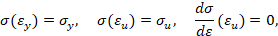
где s - нормальное напряжение, e - относительное удлинение (относительная деформация), E - модуль упругости, e_y - относительная деформация при пределе текучести, e_u - относительная деформация при пределе прочности.

Прямая параболическая аппроксимация (вариант 2). Будем считать, что кривая упрочнения проходит через предел текучести, предел прочности и имеет заданный модуль упрочнения при пределе текучести. В этом случае аналитическое описание кривой упрочнения имеет вид

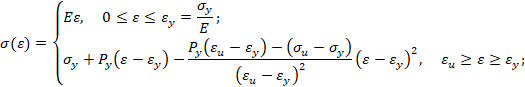
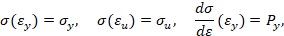
где P_y - модуль упрочнения при пределе текучести.

Обратная параболическая аппроксимация (вариант 1). Будем считать, что кривая упрочнения проходит через предел текучести, предел прочности и имеет максимум в пределе прочности (в момент образования шейки образца). В этом случае аналитическое описание кривой упрочнения имеет вид

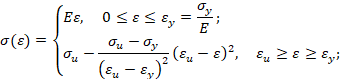
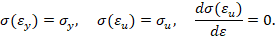
Обратная параболическая аппроксимация (вариант 2). Будем считать, что кривая упрочнения проходит через предел текучести, предел прочности и имеет заданный модуль упрочнения при пределе текучести. В этом случае аналитическое описание кривой упрочнения имеет вид

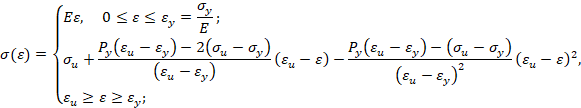
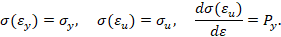
Прямая кубическая аппроксимация. Будем считать, что кривая упрочнения проходит через предел текучести, предел прочности, имеет максимум в пределе прочности (в момент образования шейки образца) и заданный модуль упрочнения при пределе текучести. В этом случае аналитическое описание кривой упрочнения имеет вид

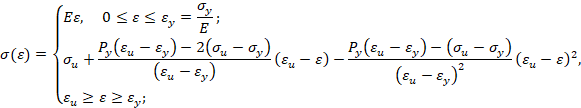
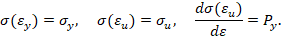
Обратная кубическая аппроксимация. Будем считать, что кривая упрочнения проходит через предел текучести, предел прочности, имеет максимум в пределе прочности (в момент образования шейки образца) и заданный модуль упрочнения при пределе текучести. В этом случае аналитическое описание кривой упрочнения имеет вид

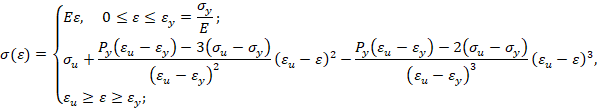
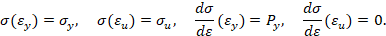
Экспериментальные кривые. Рассмотрим детально особенности экспериментальной диаграммы статического растяжения стального образца.

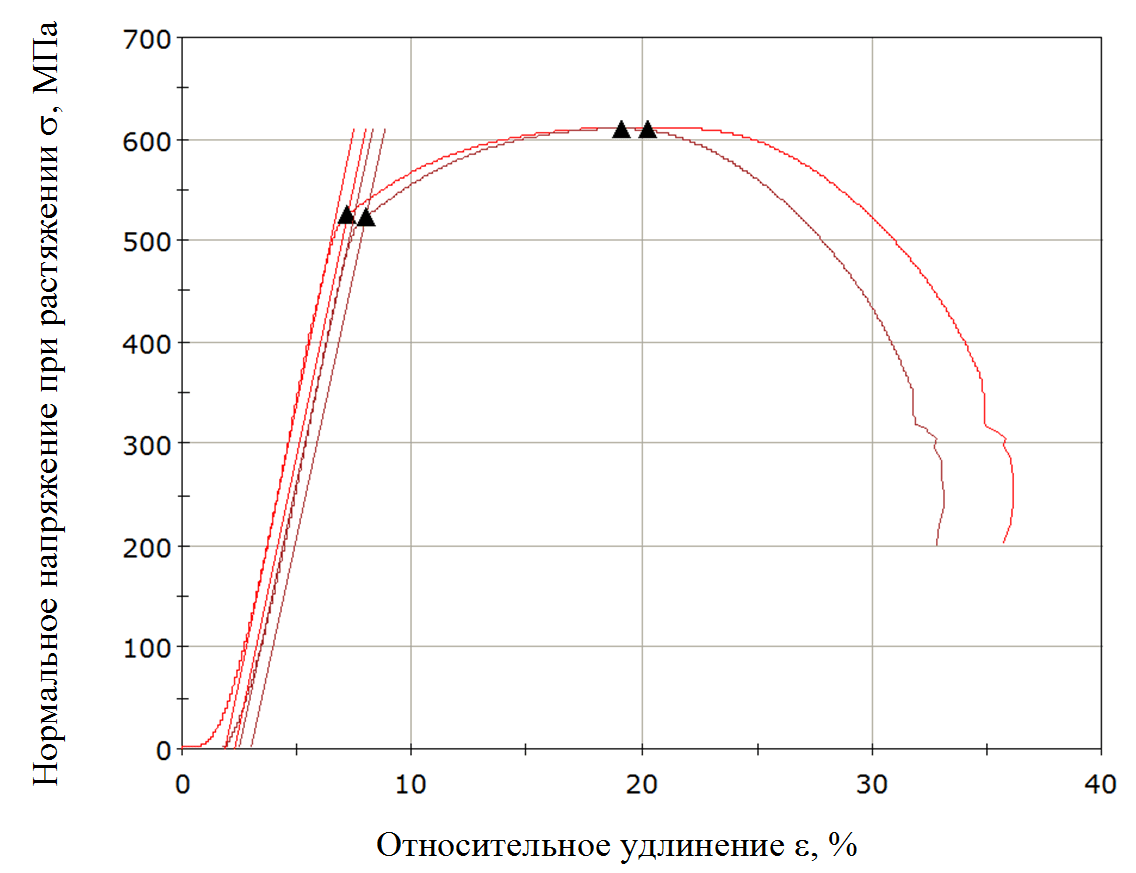
Рис. Диаграмма растяжения стальных образцов класса прочности 485

На рисунке показаны результаты механических испытаний (диаграмма растяжения) двух плоских образцов из трубной стали класса прочности 485. Длина и ширина образцов соответственно равна 180 мм и 39,8 мм, температура испытания +20 °С, методика испытания ISO 6892. Результаты испытания образцов: условный предел текучести s_0,5 (0,5 %) для образцов соответственно равен 523 МПа и 525 МПа, предел прочности - 612 МПа и 610 МПа, относительное удлинение образцов в момент разрыва - 27 % и 22 %, отношение предела текучести к пределу прочности - 0,858 и 0,857.

Из рисунка отчетливо видно, что кривая упрочнения на диаграмме растяжения имеет явно нелинейный характер. Производная (тангенс угла наклона) кривой напряжения в точке, соответствующей пределу текучести стали, имеет «излом» и некоторое конечное (не бесконечное) значение. В зоне упрочнения кривая напряжения является выпуклой монотонно возрастающей кривой, имеющей максимум (нулевую производную) в точке, соответствующей пределу прочности (в момент образования шейки).

Иногда в начале зоны упрочнения может наблюдаться небольшая площадка текучести, когда удлинение стержня происходит при почти постоянном значении растягивающей силы. Длина площадки текучести несравнимо меньше размеров зоны упрочнения, поэтому площадкой текучести при практических расчетах обычно можно пренебречь. На рисунке площадка текучести не видна.