Теплообмен при электроконвективном течении трансформаторного масла в круглой трубе

Круглые трубы часто встречающийся элемент теплообменных аппаратов, в том числе и электроэнергетических, например, охлаждающие трубчатые радиаторы кожухов силовых трансформаторов. Именно эти элементы при протекании жидкости отдают тепло, выделяющееся при работе устройств в окружающую среду и определяют, тем самым, эффективность охлаждения.

В настоящей работе приведены результаты исследования теплообмена в круглой трубе при течении в ней трансформаторного масла под действием электрического поля [1]. Такое движение получено в экспериментальной установке, разрез которой приведен на рисунке 1. В теплоизолированный сосуд, заполненный трансформаторным маслом впаяна медная теплообменная трубка 3, игла 2 расположена коаксиально трубе у ее торца. Между трубой и иглой подавалось постоянное напряжение источника [2, с. 123-125; 3, с. 241-242; 4, с. 43-47].

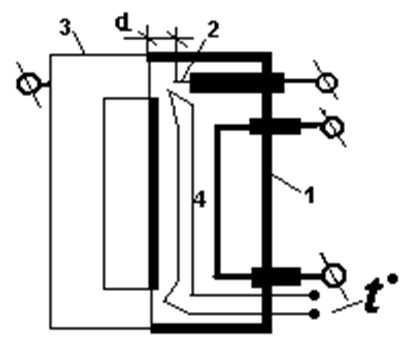
Рис. 1. Схема экспериментальной установки для изучения электроконвективного теплообмена в трубе: 1 – резервуар, 2 – игольчатый электрод, 3 – теплообменная трубка, 4 – нагреватель, d – расстояние между острием иглы и торцом трубки. U – клеммы подключения высокого напряжения, t° – клеммы дифференциальной термопары

Методика экспериментов состояла в нахождении относительного коэффициента теплоотдачи от трансформаторного масла к трубе [5, с. 143-144; 6, с. 140-143; 7, с. 182-184]. Для этого устройство выдерживалось для достижения стационарного режима охлаждения в условиях естественной конвекции, при котором определялся коэффициент теплоотдачи. После этого воздействуя на охлаждающую среду электрическим полем, создавалось её круговое движение через трубу и сосуд, а по достижении устройством стационарного режима вновь находился коэффициент теплоотдачи.

Первоначальные визуальные наблюдения позволили установить, что вихревое движение масла у острия иглы начинается уже при напряжениях чуть больше 1 кВ, однако, в этих условиях влияния на теплообмен не обнаруживалось.

Эксперименты в области тепловых потоков 20¸150 кВт/м², показали, что рост коэффициента теплоотдачи a происходит при определенных пороговых напряжениях, значительно выше тех, при которых отмечается движение у острия иглы.

Увеличение разности потенциалов между иглой и теплоотдающей трубкой, начиная с порогового, приводили к возрастанию коэффициента теплоотдачи  и соответствующему уменьшению температуры нагревателя (рис. 2).

Рис. 2. Зависимость относительного коэффициента теплоотдачи от напряжения U между иглой и трубкой. Расстояние между острием иглы и торцом трубки d составляет: кривая ---- – 5 мм, кривая ´ – 2 мм, кривая   – -5 мм. Тепловой поток 75 кВт/м². Температура трансформаторного масла 35°С [3, с. 241-242; 4, с. 43-47]

Рис. 3. Зависимость коэффициента теплоотдачи a в трансформаторном масле от межэлектродного напряжения U. Удельный тепловой поток составляет q=120 кВт/м², средняя температура жидкостей t=35°C [3, с. 241-242; 4, с. 43-47]

Окончательно можно сказать, что рост скорости и коэффициента a вместе с межэлектродным напряжением наиболее резкий, когда длина участка иглы, контактирующего с жидкостью, составляет значение порядка 3 мм, что соответствовало 4-5 наибольшим ее диаметрам. По достижении этой длины с дальнейшим ее ростом расходная скорость оставалась практически неизменной, хотя коэффициент теплоотдачи слабо рос, по линейной зависимости. Причина роста коэффициента a на этом участке, как показали визуальные наблюдения, обуславливается интенсивным радиальным движением жидкости по всему объему теплоизолированного сосуда, что приводило к перемешиванию жидкого диэлектрика и созданию в сосуде дополнительных конвекционных потоков.

Так как, в этом случае наблюдались интенсивные радиальные игле потоки, то, очевидно, возрастало гидродинамическое сопротивление в начальном участке теплоотдающей трубки, что приводило к незначительному уменьшению скорости вдоль оси иглы и появлению некоторого уменьшения величины расходной скорости.

Для получения универсальных характеристик электроконвективного теплообмена в трубах изучено влияние длины и диаметра самих теплоотдающих труб на теплообмен с окружающей средой. Исходными параметрами были те, которые легко определялись в опытах – числа Прандтля, Пекле, Рейнольдса.

В опытах использовали тот же прямоугольный теплоизолированный сосуд с нагревателем и систему съемных теплоотдающих каналов со следующими размерами: длина 0,07 и 0,23 м, диаметр 0,0028 м; длина 0,102 и 0,155 м, диаметр 0,005 мм, длина 0,102 м и диаметры 0,006 и 0,01 м.

Измерялась разность температур на входе и выходе теплоотдающего канала. Безразмерный фактор Динома К, определяемый диаметром d самого канала и радиусом его закругления R:

, (1)

В опытах не превышал значений 12, поэтому искривление труб в проводимых экспериментах мы не учитывали.

На рисунке 4 приведена зависимости коэффициента теплоотдачи от диаметра трубчатого канала при постоянной длине его оси. Как видно из рисунка наблюдается монотонное увеличение интенсивности теплоотдачи с ростом диаметра, однако, прибавка к числу Нуссельта оказывается меньше, чем следует ожидать согласно [8] при постоянном межэлектродном напряжении, в аналогичных тепловых условиях.

На рисунке 5 изображены зависимости коэффициента теплоотдачи в окружающую среду от трубок разной длины при фиксированном диаметре. Во всех случаях рост длины трубы увеличивал интенсивность передачи тепла в окружающую среду. Причем в области малых длин числа Нуссельта превышали таковые, вычисленные по [8] (2) для трубок большей длины.

Рис. 4. Зависимость числа Нуссельта от диаметра канала. Точки – экспериментальные данные при межэлектродном напряжении 6 кВ. Линия – результат обсчета по (2) при Re=9.5

Рис. 5. Зависимость среднего числа Нуссельта от длины канала диаметром 3 мм. Линии – результат расчета по (2) при числах Рейнольдса 9.5 (сплошная кривая) и 20 (пунктир). Точки – экспериментальные данные: ´ – при 10 кВ, o – при 22 кВ

Среднее число Нуссельта для теплообмена в канале длиной l при постоянной температуре окружающей среды дается аппроксимирующей функцией [8]:

, (2)

В экспериментах число Рейнольдса не превышало 40, поэтому течение можно было считать ламинарным, что являлось основанием для использования соотношения (2).

Обнаружено, что при электроконвективном течении число Нуссельта, характеризующее теплообмен более резко зависит от числа Рейнольдса, измеренного на выходе теплообменного канала (рис. 6). Точки на графиках рисунка получены путем обработки экспериментальных результатов серий опытов с различными каналами. Такая закономерность может быть объяснена только возникновением в движущемся потоке вихревых движений жидкого диэлектрика, отклоняющих его от осевого движения вдоль трубы.

Действительно, развитие электрогидродинамического течения связано с наличием градиента давления. Он возникает в жидком диэлектрике благодаря формированию в начальном участке трубы вихревого течения у самого острия иглы. Результатом такого вихревого течения будет, очевидно, «удлинение» гидродинамического начального участка, где устанавливается профиль скоростей и течение переходит в ламинарное. Следствием этого эффекта будет локальное повышение теплопередачи в окружающую среду от начального термического участка трубы, а учитывая еще и большую длину этого участка, приходим к выводу о повышении интегральной теплоотдачи в потоке жидкости в этом удлиненном начальном гидродинамическом участке

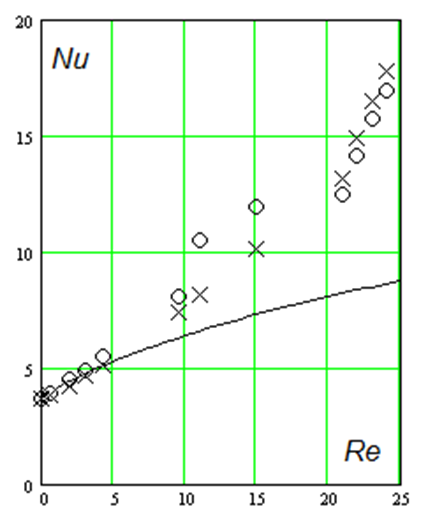
Рис. 6. Зависимость числа Нуссельта при электроконвективном теплообмене в канале от числа Рейнольдса, найденного по расходной скорости на выходе канала. Точки - экспериментальные данные. Линия – расчет согласно формулы (2)

Так как турбулентные и возвратные течения более выражены при высоких напряжениях, то более резкий рост интегрального числа Нуссельта (рис. 6) наблюдается при больших числах Re, которым соответствуют высокие потенциалы иглы, то есть при развитом электроконвективном течении.

Интегральное число Нуссельта в диапазоне средних значений напряженности электрического поля (от 0 до 50 МВ/м) в рассматриваемом случае можно выразить соотношением:

, (3)

Где первое слагаемое выражает перенос тепла за счет осевой скорости, а второе за счет появления радиальной компоненты при электроконвективном движении.

Очевидно, на радиальную компоненту особое влияние должно оказывать расположение иглы по отношению к теплоотдающему каналу, а также соотношение их диаметров. Однако, последний фактор, по результатам опытов оказался вовсе незначительным. Особое значение здесь имеет диаметр острия иглы, то есть градиент электрического поля.

Необходимо отметить, что приведенная на рисунке 6 зависимость вполне объяснима, так как поперечный D и продольный L размеры вихревого течения вблизи игольчатого электрода, зависят от приложенного напряжения согласно соотношениям L=10^-3×(1.5¸2)×U и D=1.5×L [9, 10].

Полученные результаты могут оказаться полезными при проектировании устройств, интенсифицирующих теплообмен в силовых масляных трансформаторах, где применяют конвекцию для охлаждения.