Богатое научное наследие по коническим сечениям оставил нам Аполлоний Пергский, крупнейшим трудом которого является книга «Конические сечения». При пересечении конуса с определёнными плоскостями на сечении образуются эллипс, парабола или гипербола.
Одним из видов конических сечений является парабола, и её применение можно наблюдать как в технике, так и в живой природе. В технической сфере параболы находят применение, например, в конструкции параболических антенн. Учитывая, что мы живём в эпоху, когда невозможно представить жизнь без технологий, становится очевидным, насколько велика значимость конических сечений [1, 3].
Далее рассмотрим решение задач, связанных с коническими сечениями, в современной геометрии. Пусть дана некоторая плоскость П, кривая второго порядка L и точка M0.
Определение. Пучок прямых, проходящих через точку M0 и пересекающих кривую второго порядка L, называется конусом [2]. Здесь точка M0 – вершина конуса, а кривая L – направляющая конуса.
Теперь рассмотрим основную задачу – выведение уравнения конуса. Пусть направляющая конуса лежит в плоскости YOZ, а вершина конуса M0 имеет координаты, не принадлежащие этой плоскости YOZ.
Возьмём произвольную точку M на прямой, проходящей через вершину M0. Обозначим точку пересечения образующей конуса с кривой L как M1.
Из условия, что точки M0, M1, M, лежат на одной прямой, следует определённое соотношение между их координатами.
Подставляя координаты точек M0, M1, M в это уравнение, получаем следующее выражение для уравнения конуса:
| (1) |
Теперь значение x1 в точке M1 равно нулю. Подставив это в соответствующее уравнение ![]() , найдём значение параметра
, найдём значение параметра ![]() :
:
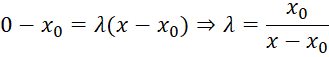 , (2)
, (2)
Подставив значение ![]() вместо x1 и y1, получим следующие уравнения:
вместо x1 и y1, получим следующие уравнения:
| (3) |
На основе полученных уравнений мы приходим к уравнению конуса.
Теперь выведем уравнение конуса 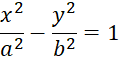 , направляющая которого является гиперболой
, направляющая которого является гиперболой ![]() , а вершина задана:
, а вершина задана:
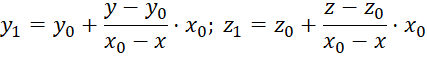 , (4)
, (4)
Подставив координаты ![]() в уравнения, упрощаем выражения:
в уравнения, упрощаем выражения:
| (5) |
Подставив упрощённые значения y1 и z1 в выражение:
| (6) |
Таким образом, получаем уравнение конуса.
Задача 1. Составить уравнение конуса ![]() , вершина которого расположена в заданной точке
, вершина которого расположена в заданной точке ![]() , а образующие образуют заданные углы 450 с данной плоскостью.
, а образующие образуют заданные углы 450 с данной плоскостью.
Решение:
| (7) |
Задача 2. ![]() построить уравнение кругового конуса, касающегося сферы.
построить уравнение кругового конуса, касающегося сферы.
Решение:
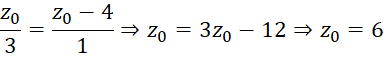 , (8)
, (8)
Следовательно, координаты вершины конуса равны ![]() :
:
| (9) |
Ответ: ![]() .
.
Задача 3. Составить уравнение конуса ![]() , вершина которого расположена в заданной точке
, вершина которого расположена в заданной точке ![]() и который касается сферы.
и который касается сферы.
Решение:
| (10) |
Ответ: ![]() .
.
Задача 4. Найти уравнение конуса ![]() , вершина которого находится в заданной точке
, вершина которого находится в заданной точке 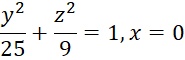 , а направляющая задана системой уравнений.
, а направляющая задана системой уравнений.
Решение:
| (11) |
Ответ: ![]() .
.
Задача для самостоятельного решения. Составить уравнение кругового конуса ![]() , вершина которого расположена в заданной точке
, вершина которого расположена в заданной точке ![]() , ось перпендикулярна заданной плоскости, а образующая образует угол 300 с осью конуса.
, ось перпендикулярна заданной плоскости, а образующая образует угол 300 с осью конуса.
Ответ: ![]() .
.
.png&w=384&q=75)
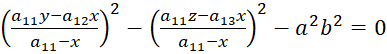 ,
,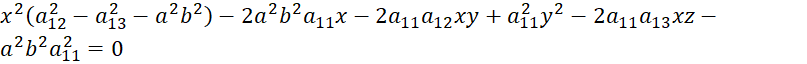
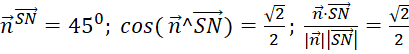 ,
,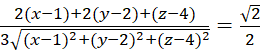 ,
,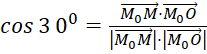 ,
,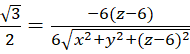 ,
,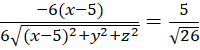 ,
,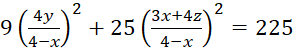 ,
,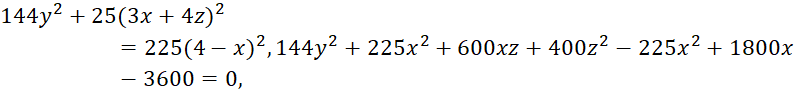
.png&w=640&q=75)