Введение
В данной работе исследуется оптимальное управление КА при спуске в атмосфере Юпитера. Сделано предположение, что искомая траектория принадлежит к классу «траекторий с отражениями». Для оценки эффективности снижения тепловых нагрузок на КА, определения оптимального управления КА и определения номинальной траектории исследуются двухпараметрические способы управления спускаемыми аппаратами в атмосфере Юпитера при помощи совместного управления углами крена и атаки. Для решения многокритериальной задачи глобальной оптимизации в условиях несовместности частных критериев оптимальности, используется аппроксимация фронта Парето. Данный подход может обеспечить существенный выигрыш по ряду ключевых параметров при спуске КА в атмосфере Юпитера.
Постановка задачи Парето-аппроксимации
Пусть совокупность частных критериев оптимальности fi(X), i ∈ [1:|F|] образует векторный критерий оптимальности F(X) ∈ {F}, где X ∈ {X} – вектор варьируемых параметров; {X}, {F} – пространства параметров и критериев соответственно. Здесь и далее запись вида |F| , где F – некоторый вектор или счетное множество, означает размерность этих объектов. Положим, что ставится задача минимизации каждого из частных критериев в одной и той же области допустимых значений DX ⊂ R|X|. Тогда задачу многокритериальной оптимизации условно записываем в виде
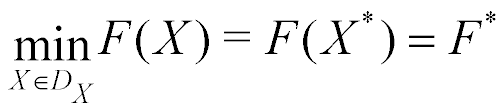 (1)
(1)
где X*, F* ‑ решения задачи. Полагаем, что частные критерии оптимальности нормализованы, так что для всех X ∈ DX справедливы соотношения fi(X) ∈ [0; 1], i ∈ [1:|F|].
Множество достижимости задачи (1) обозначаем DF , а множество Парето и фронт Парето – DX*, DF* соответственно. При этом фронтом Парето DF* является нижняя граница оптимального по Парето множества DX*. Ставим задачу приближенного построения множества Парето (а, тем самым, и фронта Парето) в задаче многокритериальной оптимизации (1). Называем эту задачу задачей Парето-аппроксимации.
Здесь и далее точка F'(X') ∈ DF является не доминируемой и входит в множество Парето, если не существует F'(X') ∈ DF такой, что fi(X) ≤ fi(X'), для всех i ∈ [1:|F|] для хотя бы одного i.
Пусть тем или иным образом уже сформировано архивное множество AF, содержащее не доминируемые точки FiA, а также архивное множество AX соответствующих ему точек XiA; i ∈ [1: |A|], |A| = |AF| = |AX|. Если при этом на итерации t появляется новая точка Fj, доминирующая некоторые точки из архива AF , то все доминируемые точки, а также соответствующие точки из архива AX, удаляем. При удовлетворении некоторого критерия останова текущее содержимое архивов AF, AX полагаем искомой аппроксимацией фронта Парето DF* и множества Парето DX* соответственно.
В популяционных методах Парето-аппроксимации новые точки для архивов AF, AX «поставляет» популяция S особей si, текущие координаты которых в пространстве поиска {X} равны Xi , а в пространстве {F} – Fi = F(Xi); i ∈ [1: |S|]. Миграция особей в пространстве поиска в популяционных алгоритмах оптимизации подчинена задаче минимизации (для определенности) значений некоторой фитнесс-функции ϕ(X) [1].
В данной работе можно интерпретировать особь si как траекторию спуска КА, полученную при единичном расчете, а популяцию S - как множество всех траекторий, полученных на одной итерации.
Фитнесс-функцию ϕ(X) строим с помощью алгоритма недоминируемой сортировки (Non-Dominated Sorting, NDS). Положим, что все частные критерии оптимальности являются одинаково важными. Ранг особи si, i ∈ [1: |S|] в его текущем положении Xi обозначаем ri. В алгоритме NDS используется простейшее из правил вычисления рангов, имеющее следующий вид.
1. Выбираем среди всех особей популяции недоминируемых, присваиваем им ранг, равный единице, и исключаем из дальнейшего рассмотрения.
2. Среди оставшихся особей выбираем недоминируемых, присваиваем им ранг, равный двум, и исключаем из дальнейшего рассмотрения. И так далее до исчерпания популяции.
Приспособленность особи Si вычисляем по формуле [2]
ϕ(Xi)=1/(1+ri), i ∈ [1: |S|].
Фронт Парето строится при помощи популяционного алгоритма многокритериальной оптимизации Big Bang-Big Crunch [3].
Постановка двухкритериальной задачи управления спуском КА в атмосфере Юпитера
Математическую модель объекта управления представляет система обыкновенных дифференциальных уравнений (ОДУ) [4, 5]:
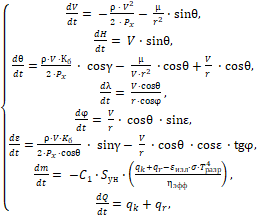 (1)
(1)
r=R+H,
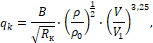
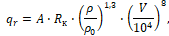
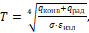 (2)
(2)
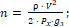 (3)
(3)
Приняты следующие условные обозначения: V – скорость КА, км/c; θ – угол наклона вектора скорости к местному горизонту, градусы; ε – угол между проекцией вектора скорости на местный горизонт и местной параллелью, градусы; H – высота полета КА над поверхностью Юпитера, км; λ и φ – джовицентрические долгота и широта соответственно, градусы; m – масса КА, кг; Q – тепловой поток, кДж/см2; R – экваториальный радиус Юпитера, км (R = 69911 км); ρ – плотность атмосферы, кг/м3 ; μ – произведение постоянной притяжения на массу Юпитера, км3/сек2 , (μ = 126686534 км3/сек2); r – радиус-вектор в ареоцентрической экваториальной системе координат, км; Px – приведенная нагрузка на лобовую поверхность КА, кг/м2 ; Кб – аэродинамическое качество; γ – угол крена, градусы; α – угол атаки, градусы; T – температура в критической точке, К; n – перегрузка; Tразр – температура разрушения материала теплозащитного покрытия, К, (Tразр=1927 К); C1 – теплоемкость материала теплозащитного покрытия, ккал/м·с·град (C1=0 при T(t)<Tразр, C1=0,4 при T(t)≥Tразр); Sун – площадь уноса, м, (Sун=4,3 м); qk – конвективный тепловой поток, кДж/см2; qr – радиационный тепловой поток, кДж/см2; A, B – коэффициенты поглощательной способности материала теплозащитного покрытия; σ – постоянная Стефана-Больцмана (σ=5.6696 ∙ 10-12 Вт ∙ см-2 ∙град-4); εизл – коэффициент, характеризующий излучательную способность теплозащитного материала (εизл = 0,9); ηэфф – эффективная энтальпия, ккал/м, (ηэфф = 1000); g3 – ускорение свободного падения на поверхности Земли, км/сек2 , (gз = 9.8 · 10-3 км/сек2).
Согласно имеющимся материалам [6], приближенно можно принять: B = 1,291·105 Дж/м3/2ч, A=3,035·107 Вт/м2.
Шкала высот атмосферы Юпитера сильно зависит от высоты h относительно уровня, на котором давление окружающего газа p = 1 бар, а соответствующая плотность ρ = ρ0 = 1,7 ∙ 104 г/см3 [7]. Примем данную высоту нулевой уровень (границу облаков). На высотах, где p > 1 бар, атмосфера Юпитера изотермична [8], а распределения давления и плотности достаточно хорошо аппроксимируется экспоненциальной зависимостью. Плотность меняется для p < 1 бар, h > 0 по закону
ρ = ρ0 = ехр(-h/Δ),
где Δ – масштаб неоднородности атмосферы, Δ ~ 23,5 км [9]; для p > 1 бар, h ≤ 0
ρ = ρ0 = (1 - h/Δ)2,27,
где Δ – масштаб неоднородности атмосферы, Δ ~ 75 км [10];
Для формы аппарата типа «несущий корпус» аэродинамические характеристики могут быть аппроксимированы следующими аналитическими зависимостями:
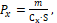 (4)
(4)
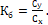 (5)
(5)
Управление КА в атмосфере осуществляется путем изменения углов крена γ и атаки α. Значения γ и α могут варьироваться в пределах:
-π≤γ≤π, 0 ≤ α ≤αmax (6)
Начальная точка траектории t = t0 соответствует моменту входа КА в атмосферу планеты, конечная точка траектории является моментом достижения поверхности планеты, либо моментом достижения высоты, на которой атмосферное давление достигает одной земной атмосферы. При этом все значения параметров КА известны.
V(t0) = V0,θ(t0) = θ0,ε(t0) = ε0,ε(t0) = ε0,h(t0) = h0,λ(t0) = λ0,ϕ(t0) = ϕ0 (7)
Определены функционалы оптимальности управления:
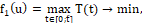 (8)
(8)
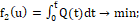 (9)
(9)
имеющие смысл максимальной температуры и суммарного теплового потока соответственно. Здесь t ̂ – длительность полета; Du={u(τ)} – множество допустимых управлений.
Задача состоит в определении допустимого управления u* (τ) ∈ Du, удовлетворяющего на решениях системы (1) условиям (8), (9).
Задача (1) - (9) представляет собой двухкритериальную задачу оптимального управления [11].
Разобьем интервал [0; t ̂ ] на равные отрезки с узлами τi, i ∈ [0:|U|] и будем искать оптимальное управление u*(τ) в классе кусочно-постоянных функций. Обозначим U=(u1, u2,…,u|U|) – (|U|×1) – вектор, где ui = u(τi). Тогда задачи (12), (13) примут вид
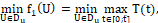 (10)
(10)
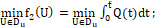 (11)
(11)
где Du={u(τ)}, i ∈ [0: |U|].
Таким образом, имеем двухкритериальную задачу оптимизации с критериальными функциями f1(U), f2(U), вектором управления U и множеством допустимых значений вектора варьируемых параметров Du.
В данной работе предложен алгоритм управления КА, обеспечивающий спуск по траектории с отражениями. В предложенном алгоритме варьируются высота условного перицентра Hπ, на которой КА меняет значения γ c 180° на 0°. Выше уровня перицентра γ принимает значение 180°, а ниже высоты условного перицентра γ равен 0°. Так же варьируются углы атаки при спуске и подъёме КА, таким образом, что α принимает при спуске КА значение αс, а при подъеме КА (отражении от атмосферы) становится равным αп. Также варьируется траекторный угол θ входа в верхние слои атмосферы.
Анализ результатов
Разработано программное обеспечение, реализующее моделирования спуска КА в атмосфере Юпитера, а также аппроксимацию фронта Парето, функционирующее под управлением операционной системы Windows 7 и выше. При разработке использована интегрированная среда разработки Qt и язык программирования высокого уровня С++.
При моделировании использовались следующие числовые значения параметров:
h(0) = 450 км, V(0) = 60 км/с, λ(0) = 0°,
Φ(0) = 0°, ε(0) = 0°, m = 500 кг.
На рисунке показана аппроксимация фронта Парето при использовании заданного алгоритма управления КА, обеспечивающего спуск по траектории с отражениями переключением углов атаки и крена при выполнении критериальных функций для КА типа «несущий корпус», полученная в результате серии вычислительных итераций.
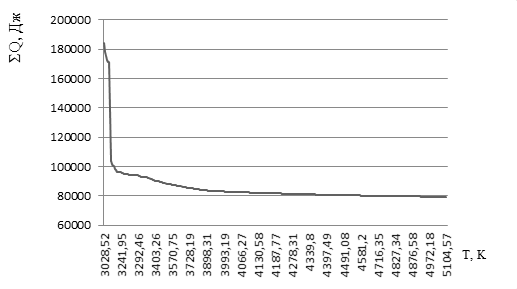
Рис. Аппроксимация фронта Парето
Как следует из определения фронта Парето – любое из решений, принадлежащее фронту Парето, не может быть улучшено одновременно по всем частным критериям оптимальности, что показано в таблице.
Таблица
Результаты моделирования
|
|
Максимальная температура, К |
Суммарный тепловой поток, кДж/см2 |
|---|---|---|
|
Оптимизация по f1(U) |
3128,95 |
171120,0 |
|
Оптимизация по f2(U) |
5073,17 |
79425,3
|
|
Компромиссный вариант |
3427,13 |
89823,8 |
ЗАКЛЮЧЕНИЕ
Разработаны методы оптимального управления КА при спуске в атмосфере Юпитера, учитывающие специфические особенности динамики полета.
Разработано программное обеспечение, реализующее моделирования спуска КА в атмосфере Юпитера, а также аппроксимацию фронта Парето, функционирующее под управлением операционной системы Windows 7 и выше. При разработке использована интегрированная среда разработки Qt и язык программирования высокого уровня С++.
Математическое моделирование показало, что предложенный алгоритм управления углом крена и углом атаки, обеспечивающий спуск по траектории с отражениями, может обеспечить существенный выигрыш по ряду ключевых параметров при спуске КА в атмосфере Юпитера. Данный алгоритм позволяет значительно снизить значения максимальной температуры и перегрузки.
Имеется возможность минимизации либо максимальной температуры, либо суммарных тепловых потоков, либо компромиссное решение, не являющееся, строго говоря, оптимальным ни по одному из частных критериев оптимальности, однако удовлетворяющее всем требованиям и ограничениям технического, либо иного характера, накладываемым на опорную номинальную траекторию. Использовать такой подход необходимо, когда другие пути нерациональны или невозможны.
Таким образом, опорную траекторию должно выбирать лицо, принимающее решение в соответствии с имеющимися техническими средствами.

.png&w=640&q=75)