Исследование динамики работы электромагнитного клапана

Введение

Электромагнитные клапаны широко используются в разных отраслях промышленности для управления потоками жидкостей и газов. Однако недостаточно изучены вопросы динамики движения якоря таких клапанов, что влияет на точность их работы и энергетическую эффективность.

Целью данного исследования является разработка математической модели, описывающей динамику движения якоря электромагнитного клапана с учетом всех основных сил, влияющих на его работу. Это актуально для улучшения точности прогнозирования поведения клапана, повышения его эффективности и снижения энергопотребления.

Для достижения поставленной цели определены следующие задачи:

1. Разработать математическую модель, учитывающую электромагнитную силу, силу пружины и силу трения, действующих на якорь электромагнитного клапана. Записать уравнение движения якоря в дифференциальной форме и решить его численным методом с помощью функции ode45 Matlab, реализующей метод Рунге-Кутта 4-5 порядка. Выполнить численное интегрирование уравнений для определения положения якоря и его скорости в функции времени.
2. Проанализировать динамику движения якоря и электромагнитной силы на основе полученных результатов численного интегрирования. Построить графики динамики положения и скорости якоря, а также динамики электромагнитной силы.
3. Оценить результативность повышения давления в пневмоаккумуляторе при политропическом процессе с использованием уравнения Бернулли для газа. Предложить направления для дальнейших исследований и усовершенствования конструкции электромагнитного клапана на основе полученных результатов.

Результаты исследования

Рассмотрена динамика движения электромагнитного клапана для обоснования математической модели, описывающей взаимодействие основных сил, влияющих на клапан. Модель позволяет рассчитать положение клапана в зависимости от времени, используя программное обеспечение Matlab для интегрирования дифференциальных уравнений, описывающих эту динамику.

Рассмотрена система, где электромагнитный клапан управляется электромагнитной силой для регулирования потока газа. Движение якоря описывается с помощью второго закона Ньютона, учитывающего силы, действующие на клапан.

В ненасыщенной магнитной системе с равномерным полем в зазоре величина электромагнитной силы вычисляется в соответствии с формулой Максвелла 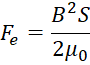[1]:

, (1)

Где индукция B определяется:

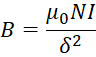, (2)

Соответственно, подставив определение индукции в формулу Максвелла получено следующее определение электромагнитной силы.

1. Электромагнитная сила Fe – это сила, возникающая в результате проходящего электрического тока через катушку электромагнита, и создающая магнитное поле [2].

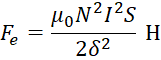, (3)

Где – магнитная постоянная [3], N=7965 количество витков катушки, I=0.057 А – ток в обмотке соответственно закону Ома I=U/r=12В/209Ом=0.057А, S=3.8∙10^-4 м² – площадь сердечника,  – расстояние между якорем и сердечником, начальное значение положения якоря 0.001 м.

2. Сила пружины F_s – это восстанавливающая сила, действующая в противоположном направлении к электромагнитной силе и пытающаяся повернуть клапан в исходное положение.

, (4)

Где x,м – перемещение якоря электромагнитна, k= 50 Н/м жёсткость пружины.

3. Сила трения F_f – сила, которая всегда противоположна движению и зависит от скорости якоря v и коэффициента трения b.

, (5)

Где v,м/c – скорость якоря электромагнита, b = 0.1 Н∙c/м коэффициент трения.

Применяя второй закон Ньютона рассчитано уравнение движения якоря электромагнитного клапана:

, (6)

Где m= 0.01 кг – масса якоря, а(м/с²) – ускорение клапана.

Раскрывая выражения для каждой силы из уравнений (3–6), получено уравнение:

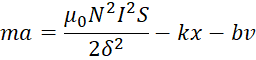, (7)

Учитывая, что 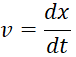и 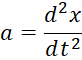запишем уравненее движения в дифференциальной форме:

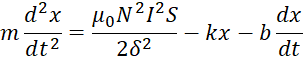, (8)

Полученное нелинейное дифференциальное уравнение второго порядка не имеет аналитического решения в общем виде, поэтому применим численный метод интегрирования. В Matlab это можно сделать с помощью функции `ode45` [4], являющейся реализацией метода Рунге-Кутта 4-5 порядка.

Результаты численного интегрирования с использованием Matlab функции `ode45` позволяют определить перемещение якоря и его скорость как функцию времени, отраженные на рисунке 1.

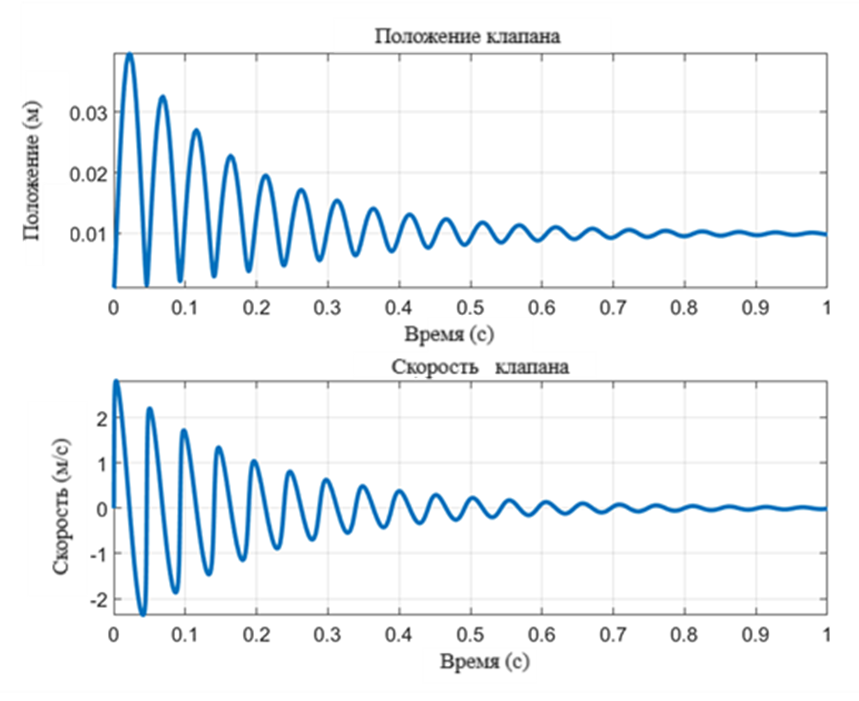
Рис. 1. Динамика положения и скорость якоря электромагнитного клапана

На графике отображена динамика изменения положения якоря электромагнитного клапана и его скорость в соответствии со временем. Первоначальное положение клапана было установлено на уровне 0.001 метра, а начальная скорость была нулевой. Время симуляции составляет от 0 до 1 секунды.

Также была определена динамика электромагнитной силы (рис. 2).

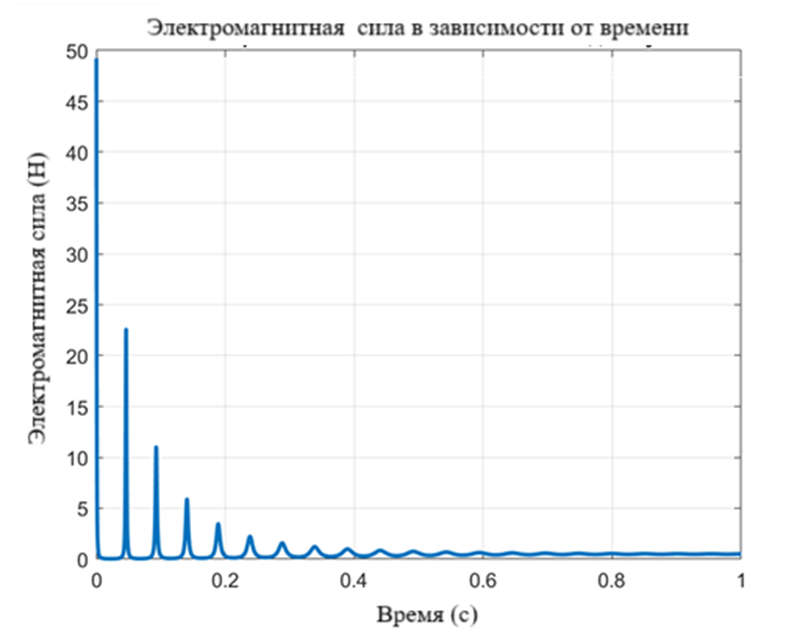
Рис. 2. Динамика электромагнитной силы на временном интервале от 0 до 1 секунды

Из рисунка 2 следует, что система испытывает затухающие колебания, что указывает на наличие в системе вязкого сопротивления. В то же время, нелинейность поведения, обусловленная зависимостью электромагнитной силы от обратно квадратичного расстояния до положения якоря, приводит к сложности управления клапаном и требует более детального анализа для совершенствования конструкции и алгоритмов управления.

Для оценки эффективности электромагнитной системы рассмотрим результативность повышения давления в пневмоаккумуляторе гидроударного устройства, например гидромолота.

Учитывая, что процесс повышения давления в камере пневмоаккумулятора политропический [5], рассмотрим параметры соотношения давлений в ресивере (камере повышенного давления) и в пневмоаккумуляторе ударного устройства (камере низкого давления) по уравнению Бернулли для газа [6, 7].

Уравнение Бернулли для газа при политропическом процессе запишется:

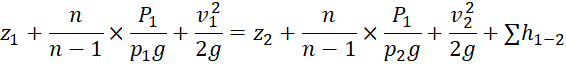, (9)

Где z₁=z₂ – нивелирные высоты (установка дополнительной емкости ресивера и пневмовкумулятора практически расположены на одном уровне), g – ускорение свободного падения, ρ₁=ρ₂ – плотность воздуха, который закачивается, например, от компрессора гидравлического экскаватора, V₁=0 – скорость газа в ресивере, V₂ – скорость газа на входе в пневмоаккумулятор; Σh_1-2 – сумма потерь напора на преодоление напора потока газа из ресивера в пневмоаккумулятор. При проведенной оценке времени разрядки ресивера принимаем Σh_1-2=0. Тогда, исходя из предыдущего уравнения, после алгебраических превращений, получим:

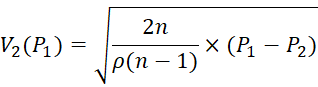, (10)

При входных данных: P₂ = 0,5´10⁶ Па – давление начальной зарядки пневмакумулятора, P₁=(0,5...10)´10⁶ Па – давление в ресивере (камере повышенного давления).

Исходя из конструктивных параметров: габаритных размеров ресивера: d=0,15 мм, l=0.6 м; а также диаметра калиброванного входного отверстия в камеру пневмоаккумулятора d₁=1 мм, геометрические параметры, соответственно, определяются:

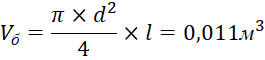, (11)

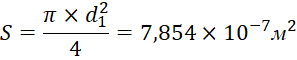, (12)

Расход газа повышенного давления из баллона ресивера:

, (13)

Время полной разрядки баллона с повышенным давлением газа составляет:

, (14)

На рисунке 3 и 4 приведены графики зависимости от давления P₁ соответственно скорости входа газа в камеру пневмоаккумулятора и времени до полной разрядки ресивера.

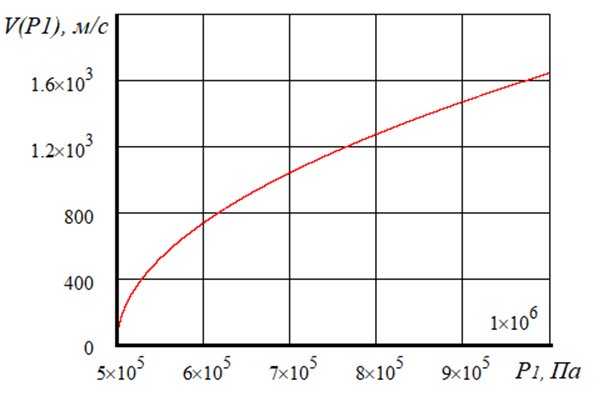
Рис. 3. График зависимости скорости входа газа в камеру пневмоаккумулятора V(P₁) от давления P₁ в ресивер

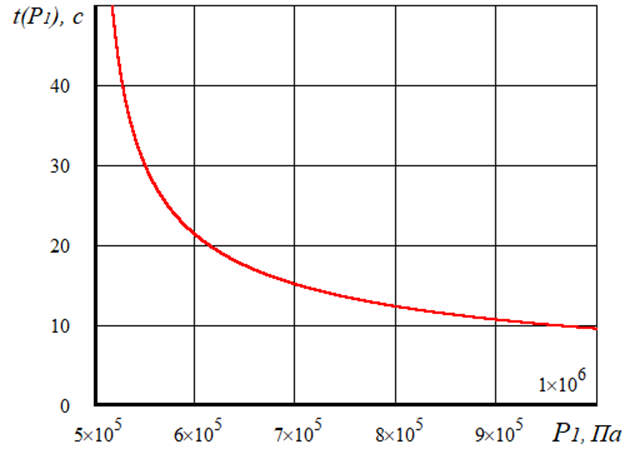
Рис. 4. График зависимости времени t(P₁)до полной разрядки ресивера от уровня в нем давления P₁

Из приведенных графиков видно, что подача порций газа в камеру пневмоаккумулятора должна быть достаточно интенсивной, а открытие канала для подачи газа должно быть кратковременно. Из расчетов электромагнитного клапана время срабатывания клапана составляет t_кл=0.05 с. Минимальное число износов определится при значении t_min=10 c составляет n_ц=t_min/t_кл= 200. То есть число случаев подзарядки пневмоаккумулятора составляет 200.

Теоретически минимальное время рабочего цикла (в соответствии с техническим паспортом на гидравлические экскаваторы ЭО-4321 и ЭО-4322) составляет t_ц=19 с.

Если включение системы адаптации на каждом цикле будет один раз, то минимальное количество времени до подзарядки баллона повышенного давления компрессором при непрерывной работе системы адаптации срставит:

, (15)

При учете переездов и изменении положения экскаватора, например, во время копания, прогнозируемое значение часов работы составит не менее 8 часов, то есть полную рабочую смену оператора.

Выводы

1. Рассмотрена динамика движения электромагнитного клапана с учетом электромагнитной силы, силы пружины и силы трения. Записано уравнение движения в дифференциальном виде и выполнено его решение с помощью функции `ode45` Matlab, которая является реализацией метода Рунге-Кутта 4-5 порядка.
2. Из полученных графиков положения и скорости электромагнитного клапана наблюдается, что максимальное отклонение клапана в начале измерений составляет около 0.04 м, которое быстро уменьшается до стабилизированного значения в районе 0.01 м в течение одной секунды. Скорость клапана варьирует в районе 2.7 м/с в начале, что указывает на первоначальное ускорение, и впоследствии замедляется до почти нулевой скорости, что свидетельствует об эффективном угасании колебаний клапана и его переходе в стабильное состояние.
3. Из графика динамики электромагнитной силы по времени установлено, что пиковое значение силы в начале наблюдения составляет 49.21 Н, после чего происходит резкое понижение до значений ниже 5 Н в течение первых 0.2 секунды. В последующие моменты сила демонстрирует угасающие колебания с постепенно уменьшающейся амплитудой и наконец стабилизируется на уровне около 0.5 Н к концу 1-секундного периода.
4. Результаты исследования могут использоваться для оптимизации параметров электромагнитного клапана, повышения его эффективности и снижения энергопотребления. Такое оптимизированное управление может способствовать увеличению надежности и продолжительности службы системы, в которых используются такие клапаны, и важно для энергетической эффективности.