Особенности исследования нелинейных систем автоматического управления

1. Введение

Нелинейные системы автоматического управления (САУ) широко применяются в технике, робототехнике, авиации и энергетике. В отличие от линейных систем, они обладают сложной динамикой, включая автоколебания, хаотические режимы и множественные состояния равновесия [1].

Цель статьи – рассмотреть современные методы анализа нелинейных САУ, их преимущества и ограничения.

2. Математическое описание нелинейных САУ

Нелинейные САУ описываются дифференциальными уравнениями вида:

, (1)

Где – вектор состояния, – управляющее воздействие, – нелинейная функция.

Примером может служить уравнение маятника с трением:

, (2)

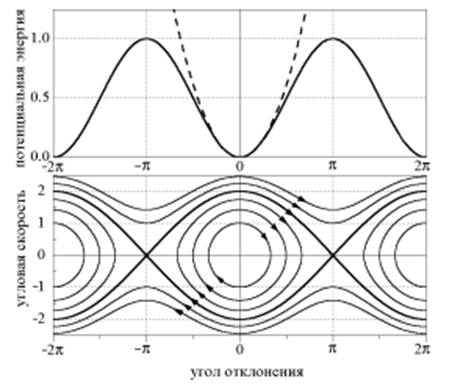
Рис. 1. Фазовый портрет нелинейного маятника [2]

3. Методы исследования нелинейных САУ

3.1. Линеаризация в окрестности точки равновесия

Линеаризация является одним из наиболее распространенных методов анализа нелинейных динамических систем. Этот подход позволяет использовать мощный аппарат линейной теории систем для исследования поведения нелинейных систем в малой окрестности точек равновесия.

Метод малых отклонений позволяет заменить нелинейную систему линейной моделью:

, (3)

Где – матрица Якоби.

3.2. Метод фазовой плоскости

Метод фазовой плоскости является одним из ключевых инструментов анализа нелинейных систем автоматического управления (САУ) второго порядка. В статье рассматриваются основные принципы построения фазовых портретов, их интерпретация, а также применение метода для исследования устойчивости и динамики нелинейных систем. Приводятся примеры анализа конкретных систем, включая маятник и релейную систему управления.

Метод фазовой плоскости – это графический способ исследования динамики систем, описываемых дифференциальными уравнениями второго порядка. Он особенно полезен для анализа нелинейных систем, где аналитическое решение часто затруднительно. Основная идея метода заключается в построении траекторий в координатах фазовой плоскости:

, (4)

Где – переменная состояния, – её производная [3].

3.3. Метод гармонического баланса

Метод гармонического баланса (МГБ) относится к частотным методам исследования нелинейных систем и позволяет определять параметры возможных автоколебаний без полного решения нелинейных дифференциальных уравнений. Метод особенно полезен для систем с существенными нелинейностями, где традиционные методы линеаризации оказываются неэффективными.

Условие баланса амплитуд и фаз формулируется в виде:

, (5)

Где – частотная характеристика линейной части, – описывающая функция нелинейности.

3.4. Функции Ляпунова

Метод функций Ляпунова, разработанный русским математиком А. М. Ляпуновым в 1892 году, остается фундаментальным инструментом анализа устойчивости нелинейных динамических систем. В отличие от методов линеаризации, этот подход позволяет исследовать устойчивость непосредственно для нелинейных систем, не прибегая к их упрощению.

Если существует положительно определенная функция , такая что , то система устойчива [4].

4. Численное моделирование нелинейных САУ

Современные пакеты (MATLAB Simulink, Wolfram SystemModeler) позволяют моделировать сложные нелинейные системы. Пример схемы в Simulink:

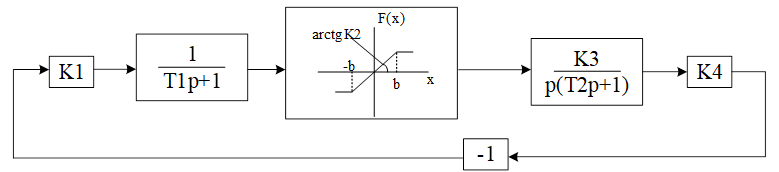
Рис. 2. Модель нелинейной системы в Simulink [5]

5. Заключение

Исследование нелинейных САУ требует комплексного подхода, сочетающего аналитические и численные методы. Перспективным направлением является применение методов машинного обучения для идентификации нелинейных моделей.