Упругопластический изгиб широко используется при производстве труб из стального листа, правке стального листа на листоправильных машинах и изделий из стального бруса [1, 2]. Для расчета силовых факторов металлургических машин при этих процессах необходимо знать численные значения изгибающего момента стального листа и бруса [2, 3]. Будем считать, что зависимость нормального напряжения s от относительной деформации e есть антисимметричная функция: s(-e) = -s(e).
Упругий изгиб бруса. Рассмотрим брус (лист) прямоугольного поперечного сечения. Пусть h и b - толщина и ширина бруса, E - модуль упругости металла бруса, sy и su - пределы текучести и прочности, d - относительное удлинение после разрыва, ey = sy/E и eu - относительные удлинения при пределе текучести и пределе прочности, Py - модуль упрочнения при пределе текучести. В марочниках сталей и сплавов [2] указаны значения sy, su и d, а значения eu и Py не указаны. Приближенно значения eu и Py для высокопрочных трубных сталей можно вычислить по формулам:
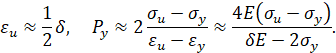
Точно значения eu и Py можно вычислить по диаграмме растяжения стали.
При упругом изгибе бруса изгибающий момент равен
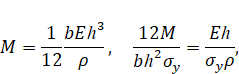
где r - радиус кривизны нейтральной плоскости бруса.
Упругопластический изгиб бруса: прямая параболическая аппроксимация (вариант 1). Пусть кривая упрочнения проходит через предел текучести, предел прочности и имеет максимум в пределе прочности. Тогда аналитическое описание кривой упрочнения имеет вид [3]
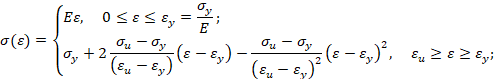
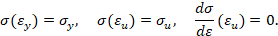
Тогда при упругопластическом изгибе бруса безразмерный изгибающий момент в поперечном сечении бруса равен
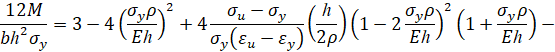
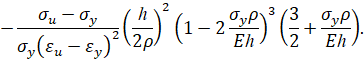
Упругопластический изгиб бруса: прямая параболическая аппроксимация (вариант 2). Пусть кривая упрочнения проходит через предел текучести, предел прочности и имеет заданный модуль упрочнения при пределе текучести. Тогда аналитическое описание кривой упрочнения имеет вид [3]
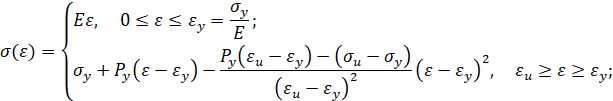
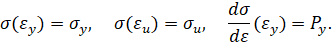
Тогда при упругопластическом изгибе бруса безразмерный изгибающий момент в поперечном сечении бруса равен
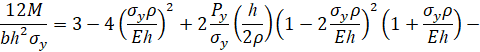
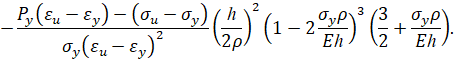
Упругопластический изгиб бруса: обратная параболическая аппроксимация (вариант 1). Пусть кривая упрочнения проходит через предел текучести, предел прочности и имеет максимум в пределе прочности. Тогда аналитическое описание кривой упрочнения имеет вид [3]
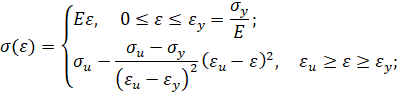
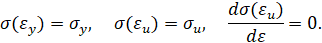
Тогда при упругопластическом изгибе бруса безразмерный изгибающий момент в поперечном сечении бруса равен
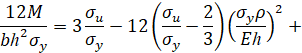
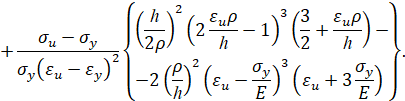
Упругопластический изгиб бруса: обратная параболическая аппроксимация (вариант 2). Пусть кривая упрочнения проходит через предел текучести, предел прочности и имеет заданный модуль упрочнения при пределе текучести. Тогда аналитическое описание кривой упрочнения имеет вид [3]
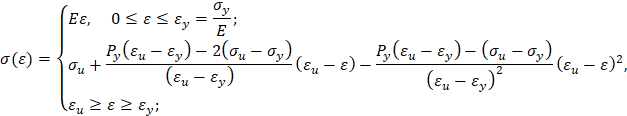
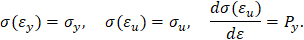
Тогда при упругопластическом изгибе бруса безразмерный изгибающий момент в поперечном сечении бруса равен
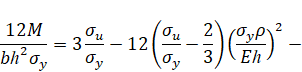
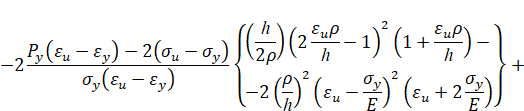
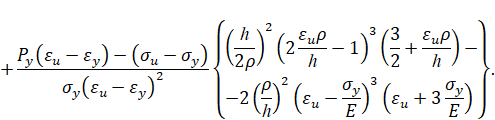
Упругопластический изгиб бруса: прямая кубическая аппроксимация. Пусть кривая упрочнения проходит через предел текучести, предел прочности, имеет максимум в пределе прочности и заданный модуль упрочнения при пределе текучести. Тогда аналитическое описание кривой упрочнения имеет вид [3]
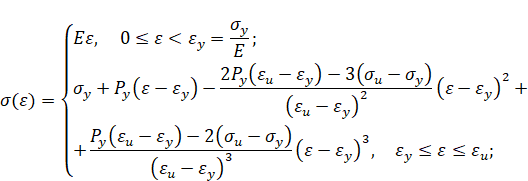
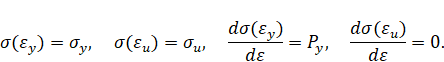
Тогда при упругопластическом изгибе бруса безразмерный изгибающий момент в поперечном сечении бруса равен

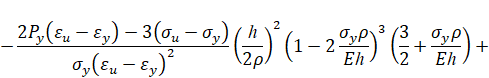
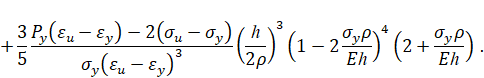
Упругопластический изгиб бруса: обратная кубическая аппроксимация. Пусть кривая упрочнения проходит через предел текучести, предел прочности, имеет максимум в пределе прочности и заданный модуль упрочнения при пределе текучести. Тогда аналитическое описание кривой упрочнения имеет вид [3]
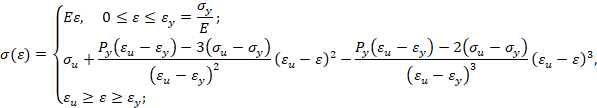
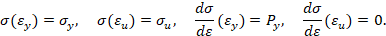
Тогда при упругопластическом изгибе бруса безразмерный изгибающий момент в поперечном сечении бруса равен
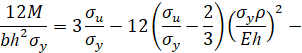
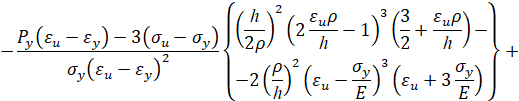
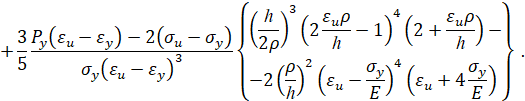

.png&w=640&q=75)