Описание упрочнения металлов при четырех граничных условиях

Классические диаграммы, описывающие зону упрочнения, - диаграмма Прандтля, линейная диаграмма, диаграммы Людвика и Надаи используют два граничных условия [1, 2]. Этого не вполне достаточно для точного описания зоны упрочнения во многих важных практических случаях (часто относительная ошибка составляет до 25 - 40 %). Параболические диаграммы зоны упрочнения, использующие три граничных условия, лучше описывают зону упрочнения. Однако наиболее точно описывают зону упрочнения кубические и степенные диаграммы (аппроксимации), использующие четыре граничных условия и учитывающие пределы текучести и прочности материала, а также модуль прочности в начале зоны упрочнения и условие максимума при достижении предела прочности (на диаграмме «напряжение - относительное удлинение»). Диаграммы с четырьмя граничными условиями практически точно (с точностью до 1 - 5 %) описывают зону упрочнения металла при растяжении. Используя эти диаграммы можно точно аналитически вычислить изгибающий момент M прямоугольного бруса (или листа) при изгибе с точностью до 5 %.

При упругом изгибе бруса безразмерный изгибающий момент равен

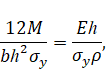
где r - радиус кривизны нейтральной плоскости бруса.

Пусть h и b - толщина и ширина прямоугольного бруса, E - модуль упругости металла бруса, s_y и s_u - пределы текучести и прочности, d и y - относительное удлинение и относительное сужение бруса после разрыва, e_y = s_y/E и e_u - относительные удлинения при пределе текучести и пределе прочности, P_y - модуль упрочнения при пределе текучести.

Обратная степенная аппроксимация. Кривая упрочнения при обратной степенной аппроксимации имеет вид

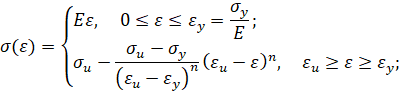
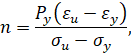
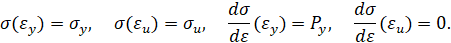
При упругопластическом изгибе бруса безразмерный изгибающий момент имеет вид

 

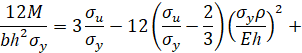
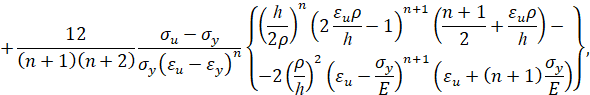
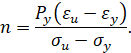
Для сталей зависимость нормального напряжения s от относительной деформации e есть антисимметричная функция [2]: s(-e) = -s(e).

Обратная полиноминальная кубическая аппроксимация. Кривая упрочнения при обратной полиноминальной кубической аппроксимации имеет вид

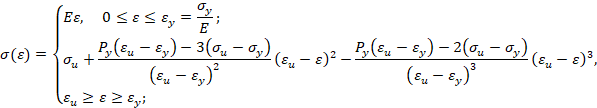
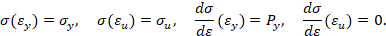
При упругопластическом изгибе бруса безразмерный изгибающий момент имеет вид

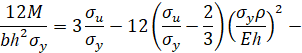
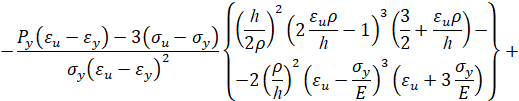
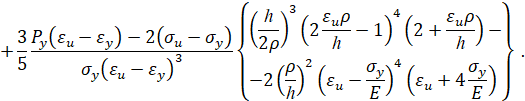
Прямая полиноминальная кубическая аппроксимация. Кривая упрочнения при прямой полиноминальной кубической аппроксимации имеет вид

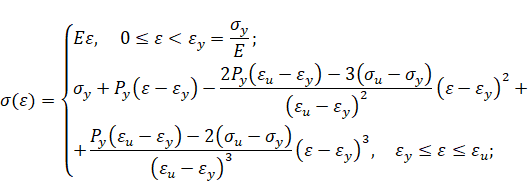
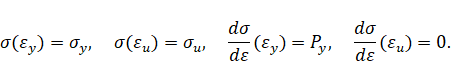
При упругопластическом изгибе бруса безразмерный изгибающий момент равен

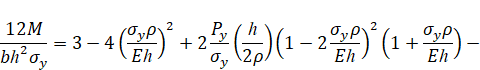
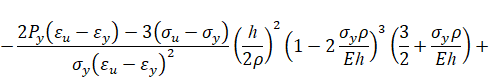
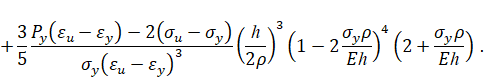
Аппроксимации модуля упрочнения и относительного удлинения при разрыве. В марочниках сталей и сплавов указаны значения s_y, s_u, d и y, а значения e_u и P_y не указаны. Приближенно значения e_u и P_y для высокопрочных трубных сталей можно вычислить по формулам:

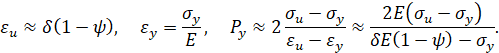
Если относительное сужение y при разрыве неизвестно (для некоторых сталей и сплавов y не указывается в марочниках сталей), то можно для относительного удлинения e_u при разрыве пользоваться формулой

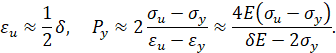
но точность определения d при этом может быть ниже.

Точно значения e_u и P_y можно вычислить по экспериментальной диаграмме растяжения стали.