БИХ фильтры и методы их проектирования

Фильтрация сигналов является одной из важнейших операций в рамках практически любой электронной системы, в том числе и цифровой. Цифровая фильтрация происходит при помощи фильтров с бесконечными и конечными импульсными характеристиками (БИХ и КИХ фильтры).

В отличие от КИХ фильтров БИХ фильтры обладают рядом преимуществ и недостатков:

• меньший порядок по сравнению с КИХ при аналогичных требованиях;
• эффективность в задачах с резкими изменениями АЧХ;
• потенциальная неустойчивость;
• нелинейная фазовая характеристика.

Наиболее сложные в аналитической реализации БИХ фильтры проектируются различными методами в зависимости от данных технического задания.

Передаточная функция БИХ фильтра – математическое его представление, которое связывает входное и выходное воздействие в дискретном времени:

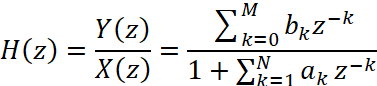, (1)

Она позволяет анализировать свойства фильтра и реализовывать его в цифровом виде.

Важным условием при проектировании фильтра является условие устойчивости – если все полюсы передаточной функции лежат внутри единичной окружности в z-плоскости, то фильтр устойчив.

Методы проектировнаия БИХ фильтров

Билинейное преобразование

Принцип метода заключается в отображении аналогового прототипа подобного фильтра в цифровую область с заменой вида:

, (2)

При проектировании задается АЧХ аналогового фильтра, например фильтра Баттерворта или Чебышева, а далее применяется само преобразование.

Инвариантное преобразование импульсной характеристики

Принцип метода заключается в сохранение импульсной характеристики аналогового прототипа.

Алгоритм проектирования заключается в получении импульсной характеристики h(t) аналогового фильтра и ее последующей дискретизации h[n]=h(nT).

Метод частотной выборки

Метод частотной выборки основан на дискретизации желаемой частотной характеристики и последующем вычислении коэффициентов фильтра через обратное дискретное преобразование Фурье.

Сравнение методов

Таблица

Сравнение методов проектирования БИХ фильтров

Пример применения метода билинейной фильтрации

В ходе работы был рассчитан фильтр методом билинейной фильтрации на основе фильтра Баттерворта. Параметры входного сигнала и фильтра приведены на рисунке 1.

Рис. 1. Параметры фильтра и сигнала для демонстрации фильтрации

После фильтрации сигнал теряет большую часть энергии, относящейся к частотам выше частоты среза. Вид сигнала до и после фильтрации приведены на рисунках 2 и 3 соответственно.

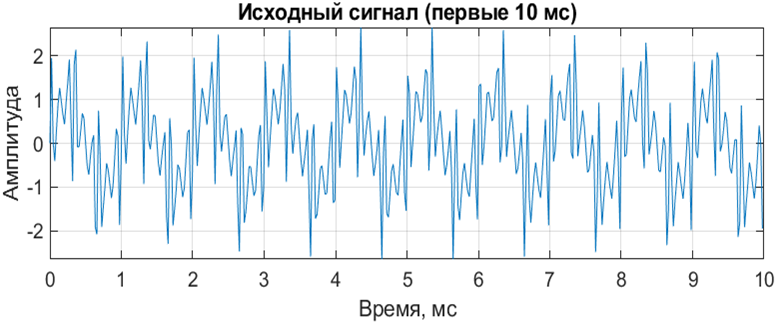
Рис. 2. Сигнал на входе фильтра

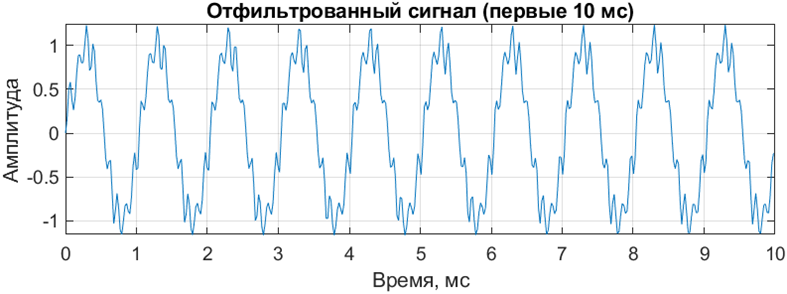
Рис. 3. Сигнал после фильтрации

На диаграмме амплитудных спектров, приведённой на рисунке 4, видно, как составляющие частоты подавляются за исключением компоненты, находящейся в полосе пропускания.

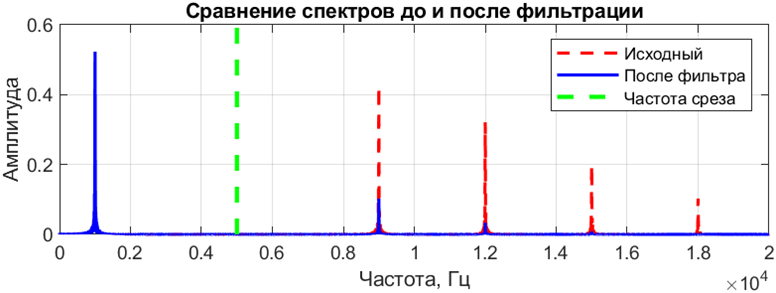
Рис. 4. Спектр входного и выходного сигналов

Параметры фильтра приведены на рисунке 5.

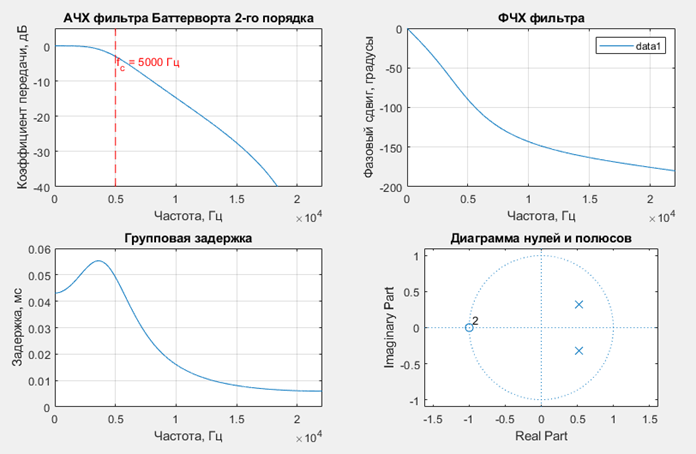
Рис. 5. Параметры полученного БИХ фильтра

При проектировании фильтра под конкретную задачу важно понимать требования, предъявляемые к полученному сигналу на выходе и от этого отталкиваться, выбирая тот или иной метод. Важно помнить такие нюансы как:

• билинейное преобразование наиболее универсально и обеспечивает устойчивость;
• инвариантное преобразование подходит для задач, где важна импульсная характеристика;
• метод частотной выборки требует осторожности из-за возможных выбросов.