Введение
Математический анализ своим основанием имеет теорию действительных чисел, поскольку объектом изучения этого раздела математики являются функции, которые заданы на множестве действительных чисел и на этом же множестве располагаются и значения функций.
В этом изложении мы будем следовать точке зрения, подробно изложенной в книге А. Лебега «Об измерении величин». В качестве наглядного представления множества действительных чисел будем иметь в виду числовую ось, на которой указано направление, выбрана точка О – положение числа ноль и единица, которая является мерой длины отрезков и дающей нам числовое представление вещественного числа, которое мы всегда будем считать десятичной дробью. Но даже при рассмотрении, в этом представлении, рациональных чисел 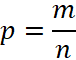 , где m целое, а n натуральное число, возникают трудности, например при рассмотрении чисел вида 0.9999999…., с бесконечным количеством цифр 9. Существует алгоритм превращения периодической десятичной дроби в обыкновенную, в котором предполагается возможность выполнения арифметических операций с числами, представленными бесконечным числом десятичных цифр, а в реальных измерениях и вычислениях всегда присутствует конечное десятичное представление величин. Очевидно, что нужно указать способ проверки равенства такого вида десятичных дробей, корректное представление результатов, а также способ проверки неравенств вида больше или меньше, именно такие задачи стоят в практических вычислениях и измерениях.
, где m целое, а n натуральное число, возникают трудности, например при рассмотрении чисел вида 0.9999999…., с бесконечным количеством цифр 9. Существует алгоритм превращения периодической десятичной дроби в обыкновенную, в котором предполагается возможность выполнения арифметических операций с числами, представленными бесконечным числом десятичных цифр, а в реальных измерениях и вычислениях всегда присутствует конечное десятичное представление величин. Очевидно, что нужно указать способ проверки равенства такого вида десятичных дробей, корректное представление результатов, а также способ проверки неравенств вида больше или меньше, именно такие задачи стоят в практических вычислениях и измерениях.
Как, хорошо известно, длины не всех отрезков числовой оси можно представить в виде рациональных чисел. Классическим примером является диагональ квадрата со стороной равной единице. Попытка представить длину диагонали в виде несократимой дроби ![]() , что мы всегда можем сделать, немедленно приводит к противоречию
, что мы всегда можем сделать, немедленно приводит к противоречию 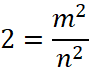 и, следовательно,
и, следовательно, ![]() и следует, что
и следует, что ![]() , является чётным числом и
, является чётным числом и ![]() делится на 4 т. е.
делится на 4 т. е. ![]() . После такой замены
. После такой замены ![]() получаем, что
получаем, что ![]() тоже четное число и, следовательно, дробь, которую мы полагали несократимой, не является таковой и, следовательно, предположение о рациональности длины диагонали квадрата неверно и такие числа называют иррациональными. Сформулируем алгоритм получения и представления числа
тоже четное число и, следовательно, дробь, которую мы полагали несократимой, не является таковой и, следовательно, предположение о рациональности длины диагонали квадрата неверно и такие числа называют иррациональными. Сформулируем алгоритм получения и представления числа ![]() и на его основе введём понятие равенства и способ корректного представления любых действительных чисел.
и на его основе введём понятие равенства и способ корректного представления любых действительных чисел.
На первом шаге определим между какими целыми числами находится наше число, поскольку ![]() и очевидно
и очевидно ![]() , далее разбивая промежуток [1,2] на десять интервалов определим интервал в котором находится
, далее разбивая промежуток [1,2] на десять интервалов определим интервал в котором находится ![]() , последовательно прибавляя 1 шаг 0,1. Установим, что
, последовательно прибавляя 1 шаг 0,1. Установим, что ![]() . На этом этапе можно записать,
. На этом этапе можно записать, ![]() с абсолютной погрешностью
с абсолютной погрешностью ![]() или кратко оценкой корня снизу 1,4, где сама форма записи (с точностью до десятых) указывает погрешность. Продолжая делить новый интервал [1,4;1,5] на десять частей, получим приближение с точностью до сотых. Таким образом мы имеем алгоритм получения
или кратко оценкой корня снизу 1,4, где сама форма записи (с точностью до десятых) указывает погрешность. Продолжая делить новый интервал [1,4;1,5] на десять частей, получим приближение с точностью до сотых. Таким образом мы имеем алгоритм получения ![]() с любой наперёд заданной точностью, а само значение корня дается приведенным алгоритмом последовательного деления интервала корня.
с любой наперёд заданной точностью, а само значение корня дается приведенным алгоритмом последовательного деления интервала корня.
Другой способ определения вычисления значения ![]() основан на делении интервала значения корня основан на методе половинного деления интервала, в котором находится значение корня и аналогичного определения интервала для отыскания следующего приближённого значения корня. Возникает вопрос, а как сравнивать результаты двух вычислений и строго определить корректность таких алгоритмов. Ответ на вопрос будет получен, если сформулировать условие равенства действительных чисел, значение которых заданы бесконечной процедурой:
основан на делении интервала значения корня основан на методе половинного деления интервала, в котором находится значение корня и аналогичного определения интервала для отыскания следующего приближённого значения корня. Возникает вопрос, а как сравнивать результаты двух вычислений и строго определить корректность таких алгоритмов. Ответ на вопрос будет получен, если сформулировать условие равенства действительных чисел, значение которых заданы бесконечной процедурой:
Определение:
Два действительных числа ![]() и β, одно из которых задано последовательностью
и β, одно из которых задано последовательностью ![]() будут равными, если для любого сколь угодно малого
будут равными, если для любого сколь угодно малого ![]() , найдётся такое N будет выполняться условие
, найдётся такое N будет выполняться условие ![]() , для всех
, для всех ![]() .
.
В математике про это определение равенства принято говорить, что последовательность сходится к числу β. Данное определение, фактически совпадает с определением предела (сходимости) последовательности. Изучение этого раздела математики представляет самостоятельный интерес, но для обоснования основных методов анализа и экономии времени достаточно ограничится таким определением.
Это определение даёт возможность корректно определить операции над любыми действительными числами, если дополнить его правилами распространения погрешности при выполнении арифметических операций.
В смысле этого определения бесконечная периодическая дробь 0,999999… просто равна единице, что совпадает со значением, полученным на основе известного алгоритма, но этот алгоритм предполагает выполнение арифметических операций над бесконечными периодическими дробями. На основе этого определения можно указать корректный способ превращения бесконечной периодической дроби в рациональное число. Проведём рассмотрение на примере дроби 0.3333…. = (0.3) + (0.3)10-1+(0.3) + 10-2……
В качестве приближения к точному значения числа будем рассматривать первые n членов этой бесконечной суммы. Данная последовательность называется геометрической прогрессией. Мы найдем сумму ![]() первых n членов и определим погрешность данного приближения, полагая что
первых n членов и определим погрешность данного приближения, полагая что ![]() .
.
| (1) |
Очевидно, что имеют место соотношения:
| (2) |
Эти соотношения будем рассматривать как систему уравнений на неизвестные ![]() , решение которой имеет вид:
, решение которой имеет вид: 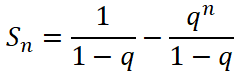 .
.
Из этого равенства следует, что точное значение дроби равно ![]() , а погрешность
, а погрешность 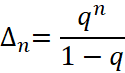 , которую можно сделать сколь угодно малым выбором соответствующего числа членов этой прогрессии, причем в N можно выбрать решив неравенство
, которую можно сделать сколь угодно малым выбором соответствующего числа членов этой прогрессии, причем в N можно выбрать решив неравенство 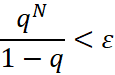 и как нетрудно видеть
и как нетрудно видеть 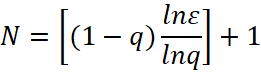 , где [x] целая часть x, а для всех
, где [x] целая часть x, а для всех ![]() неравенство будет выполняться.
неравенство будет выполняться.
Особо отметим, что если взять любую точку на вещественной оси и использовав алгоритм, приведённый при отыскании ![]() , то можем отыскать соответствующую этой точке действительное число и причем в виде десятичной дроби, что является иллюстрацией аксиомы непрерывности (полноты) множества действительных чисел. Введенное определения позволят нам последовательно рассмотреть теорию и инструменты математического анализа, не пользуясь понятием предела. Изучая основы этой теории, конечно, мы ограничиваем классы рассматриваемых функций, но класс элементарных функций, изучение которого и является целью этой работы, будет удовлетворять наложенным ограничениям.
, то можем отыскать соответствующую этой точке действительное число и причем в виде десятичной дроби, что является иллюстрацией аксиомы непрерывности (полноты) множества действительных чисел. Введенное определения позволят нам последовательно рассмотреть теорию и инструменты математического анализа, не пользуясь понятием предела. Изучая основы этой теории, конечно, мы ограничиваем классы рассматриваемых функций, но класс элементарных функций, изучение которого и является целью этой работы, будет удовлетворять наложенным ограничениям.
1. Дифференциальное исчисление
Пусть имеется функция y= f(x), введем понятие приращение функции ∆(y) и величину ∆х, называемую приращением аргумента x:
![]() , (3)
, (3)
Таким образом величина ∆(y) является функцией переменных x и ∆х, выделим их неё отдельно линейную часть ![]() , которая называется дифференциалом функции f(x), а
, которая называется дифференциалом функции f(x), а ![]() именуется производной функции f(x), а оставшуюся часть обозначим как М(x, ∆х)∆(х)2, про которую будем предполагать, что М(x, ∆х) ограничена при всех х и (М(x, ∆х)∆(х)2/∆x)=0. Именно это и есть ограничение на класс функций и этот класс естественно назвать классом дифференцируемых функций (далее мы уточним это понятие), окончательно:
именуется производной функции f(x), а оставшуюся часть обозначим как М(x, ∆х)∆(х)2, про которую будем предполагать, что М(x, ∆х) ограничена при всех х и (М(x, ∆х)∆(х)2/∆x)=0. Именно это и есть ограничение на класс функций и этот класс естественно назвать классом дифференцируемых функций (далее мы уточним это понятие), окончательно:
![]() , (4)
, (4)
Или (1.2).
![]() , (5)
, (5)
М(x, ∆х) – ограниченная функция.
Смысл такого выделения понятен, если рассматривать очень малые приращения аргумента ∆х, которые естественно обозначить dx, то величина приращение функции ∆(y) будет определяться её линейной частью, которую называют главной частью приращения или дифференциалом функции и записывать в виде ![]() (1.3), а производную определить, как отношение дифференциалов
(1.3), а производную определить, как отношение дифференциалов 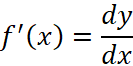 (1.4).
(1.4).
Особо отметим, что ![]() и
и ![]() , этом контексте просто переменные.
, этом контексте просто переменные.
Выясним геометрический смысл дифференциала. Для этого на рисунке 1 изобразим секущую ![]() и касательную
и касательную ![]() . Секущая проходит через т. А и т. В, касательная проходит точку с координатами (x0, y0), лежащую на средине отрезка [x1, x2].
. Секущая проходит через т. А и т. В, касательная проходит точку с координатами (x0, y0), лежащую на средине отрезка [x1, x2].
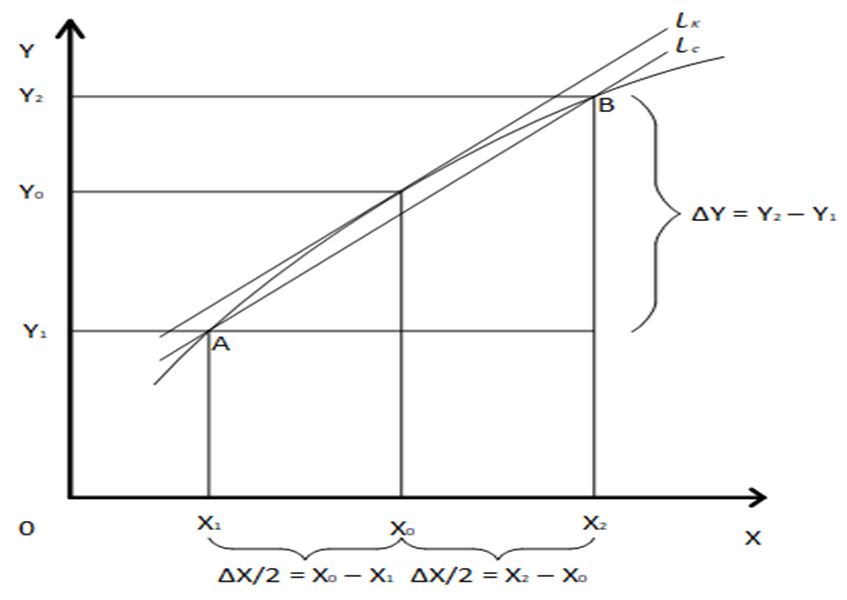
Рис. 1
Таким образом, что ![]() и
и ![]() . Выпишем уравнение секущей как уравнение прямой проходящей через точку (x1, y1) с угловым коэффициентом
. Выпишем уравнение секущей как уравнение прямой проходящей через точку (x1, y1) с угловым коэффициентом 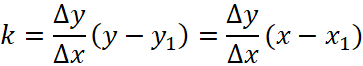 .
.
Будем сближать точки А и В друг к другу, тогда они будут приближаться к точке (x0, y0) и это сближение можно реализовать уменьшая ∆х, а угловой коэффициент, если ограничится в приращении ∆y линейным членом согласно формуле (1.2) и в силу малости ∆x будет равен ![]() и мы получим уравнение касательной к графику функции
и мы получим уравнение касательной к графику функции ![]() в точке
в точке ![]() .
.
Т. е. зная производную мы можем выписывать уравнение касательной к кривой.
Этот пример показывает важность понятий дифференциала и производной, а также показывает необходимость их вычисления, для решения такого рода задач.
Рассмотрим ряд очевидных следствий того факта, что величина приращения функции в малой окрестности точки определяется величиной дифференциала и далее будем полагать, что для всех рассматриваемых функций условие (1.2) выполнено.
Теорема 1.1
Если производная ![]() функции
функции ![]() больше нуля на отрезке [a,b], то на этом отрезке функция возрастает, если
больше нуля на отрезке [a,b], то на этом отрезке функция возрастает, если ![]() , то функция убывает.
, то функция убывает.
Доказательство: Возьмем любую точку α на отрезке [a, b] и рассмотрим приращение функции ![]() и тогда при малых ∆х знак приращения, будет определяться знаком производной, поскольку
и тогда при малых ∆х знак приращения, будет определяться знаком производной, поскольку ![]() . Поскольку для любой точки х правее α,
. Поскольку для любой точки х правее α, ![]() и
и ![]() , что и показывает возрастание. Левее точки α,
, что и показывает возрастание. Левее точки α, ![]() , поскольку
, поскольку ![]() , то и в этом случае имеем возрастание функции. Доказательство убывания
, то и в этом случае имеем возрастание функции. Доказательство убывания ![]() аналогично и не требует дополнительных пояснений.
аналогично и не требует дополнительных пояснений.
Следствием теоремы 1.1 является простая, но важная для дальнейших построений:
Теорема 1.2
Если производная ![]() функции
функции ![]() равна нулю на отрезке [a,b], то на этом отрезке функция постоянна у = const = c.
равна нулю на отрезке [a,b], то на этом отрезке функция постоянна у = const = c.
Доказательство очевидно, поскольку она в соответствии с теоремой 1.1 не возрастает и не убывает, то она является постоянной.
Определение 1.1
Будем говорить, что функция ![]() в точке x0 имеет локальный максимум (минимум), если существует окрестность этой точки
в точке x0 имеет локальный максимум (минимум), если существует окрестность этой точки ![]() , для всех точек которого имеет место неравенство
, для всех точек которого имеет место неравенство ![]() .
.
Теорема 1.3
Если производная ![]() функции
функции ![]() равна нулю в точке x0 отрезка [a,b] и изменяет знак с плюса на минус (с минуса на плюс) при переходе точки , то в этой точке имеется локальный максимум (минимум).
равна нулю в точке x0 отрезка [a,b] и изменяет знак с плюса на минус (с минуса на плюс) при переходе точки , то в этой точке имеется локальный максимум (минимум).
Эта теорема является очевидным следствием теоремы 1.1, поскольку в случае максимума она слева от точки ![]() возрастает, а справа – убывает. Для минимума справедливы такие же соображения. Существование интервала
возрастает, а справа – убывает. Для минимума справедливы такие же соображения. Существование интервала ![]() обеспечено выполнением условия (1.2).
обеспечено выполнением условия (1.2).
Рассмотрим ряд правил, которые помогут нам вычислять производную и дифференциал функций.
Дифференциал суммы функций ![]()
Выпишем наше основное предположение относительно функций в виде:
![]() , (6)
, (6)
В этом виде и запишем ![]() (аргументы M не выписываем), с другой стороны,
(аргументы M не выписываем), с другой стороны, ![]() , по определению приращения. Перегруппировав члены в этом выражении, получим
, по определению приращения. Перегруппировав члены в этом выражении, получим ![]() и использовав основное предположение в форме (6) получим
и использовав основное предположение в форме (6) получим ![]() и следовательно имеем правило:
и следовательно имеем правило: ![]() или для производных
или для производных ![]() .
.
Дифференциал от произведения функции на константу C
![]() , (7)
, (7)
Или для производных:
![]() , (8)
, (8)
Совершенно очевидное свойство и не требует дополнительных комментариев.
Дифференциал произведения функций
Пусть ![]() и рассмотрим приращение
и рассмотрим приращение ![]() . Добавим и вычтем член
. Добавим и вычтем член ![]() и перегруппируем члены:
и перегруппируем члены:
| (9) |
Оставляя линейные по ![]() члены в обеих частях равенства, получим
члены в обеих частях равенства, получим ![]() или для производных
или для производных ![]() .
.
Аналогичным образом доказывается и формула дифференциала частного двух функций.
Дифференциал частного двух функций
Просто приведем соответствующую формулу:
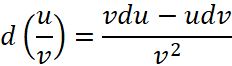 , (10)
, (10)
Или для производных:
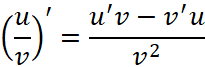 , (11)
, (11)
Дифференциал сложной функции
Пусть имеем функцию ![]() по определению дифференциала имеем, вначале дифференциал по
по определению дифференциала имеем, вначале дифференциал по ![]() , как независимой переменной и далее выпишем дифференциал
, как независимой переменной и далее выпишем дифференциал ![]() :
:
![]() , (12)
, (12)
Или для производных:
![]() , (13)
, (13)
Дифференциал обратной функции
Пусть имеется функция ![]() и будем предполагать, что обратная к ней существует, тогда её функциональная зависимость будет выражаться формулой
и будем предполагать, что обратная к ней существует, тогда её функциональная зависимость будет выражаться формулой ![]() , вычисляя дифференциал от обеих частей равенства, получим
, вычисляя дифференциал от обеих частей равенства, получим ![]() и отсюда:
и отсюда:
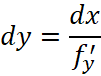 , (14)
, (14)
Или для производных:
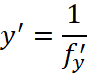 , (15)
, (15)
Естественно, в этих формулах, в выражении для производных, нужно вернуться к привычному обозначению обратной функции ![]() .
.
Мы установили ряд правил вычисления производных функций, которые удовлетворяют условию (1.2) и таким образом мы готовы выполнить программу вычисления производной любой элементарной функции, если получим таблицу производных базовых элементарных функций, которая состоит из степенной, тригонометрических и логарифмических функций. Использую правила дифференцирования мы сможем находить производную любой функции из класса элементарных, поскольку он состоит из базовых и составленных из них при помощи операций, рассмотренных нами при выводе правил дифференцирования.
В качестве примера покажем, как это общее рассмотрение можно применить к функции ![]() .
.
![]() , (16)
, (16)
Линейная по часть приращения равна ![]() , член
, член ![]() равен просто
равен просто ![]() и производная
и производная ![]() . В параграфе 3 подобным образом мы получим таблицу производных для всех базовых элементарных функций.
. В параграфе 3 подобным образом мы получим таблицу производных для всех базовых элементарных функций.
2. Интегральное исчисление
В первом параграфе мы ввели понятия дифференциала и производной функции ![]() и они связаны соотношениями:
и они связаны соотношениями:
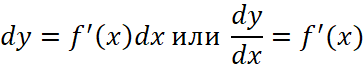 , (17)
, (17)
Поставим перед собой задачу восстановления функции ![]() по её производной
по её производной ![]() . Будем называть
. Будем называть ![]() первообразной
первообразной ![]() или неопределенным интегралом
или неопределенным интегралом ![]() и обозначать:
и обозначать:
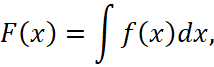 , (18)
, (18)
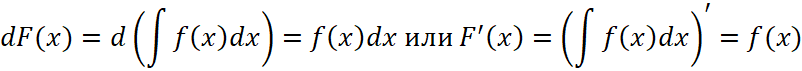 , (19)
, (19)
Где ![]() называют подынтегральным выражением, и переменная в дифференциале показывает функциональную зависимость первообразной и называют переменной интегрирования, а
называют подынтегральным выражением, и переменная в дифференциале показывает функциональную зависимость первообразной и называют переменной интегрирования, а ![]() называют подынтегральной функцией, которая может зависеть и от других переменных, называемых параметрами первообразной.
называют подынтегральной функцией, которая может зависеть и от других переменных, называемых параметрами первообразной.
Выясним сколько первообразных соответствуют одной функции ![]() .
.
Предположим, что имеются две первообразные одной функции ![]() которые обозначим как
которые обозначим как ![]() . Рассмотрим их разность и вычислим её производную
. Рассмотрим их разность и вычислим её производную ![]() , согласно теореме (1.2) эта разность есть просто константа и таким образом всё множество первообразных одной функции представляет собой совокупность вида
, согласно теореме (1.2) эта разность есть просто константа и таким образом всё множество первообразных одной функции представляет собой совокупность вида ![]() , где
, где ![]() любая из первообразных и этот факт принято обозначать как:
любая из первообразных и этот факт принято обозначать как:
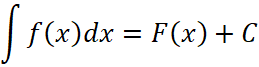 , (20)
, (20)
Выпишем ряд очевидных свойств неопределённого интеграла, вытекающих из его определения.
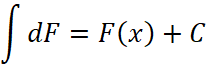 или
или 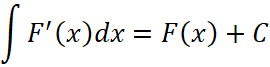 , (21)
, (21)
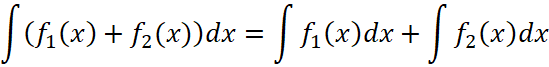 , (22)
, (22)
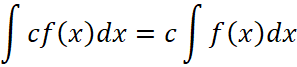 , (23)
, (23)
Убедится в правильности этих равенств можно, если взять производную или дифференциал от обеих частей равенств.
Правило подстановки или замены переменной интегрирования
Пусть известно, что 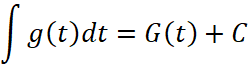 , то тогда (подстановка
, то тогда (подстановка ![]() ), дает:
), дает:
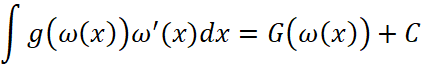 , (24)
, (24)
Это правило подстановки есть следствие правила дифференцирования сложной функции:
![]() , (25)
, (25)
Правило интегрирования по частям
Это правило есть следствие дифференцирования произведения функций, которое выпишем ![]() и проинтегрируем
и проинтегрируем 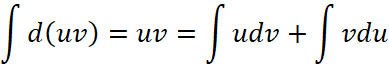 или:
или:
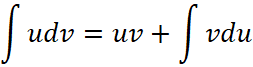 , (26)
, (26)
Определённый интеграл
Будем называть определенным интегралом 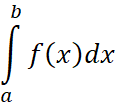 от функции
от функции ![]() в пределах
в пределах ![]() до
до ![]() , которые называются нижним и верхним пределами интегрирования, приращение первообразной
, которые называются нижним и верхним пределами интегрирования, приращение первообразной ![]() равное
равное ![]() или:
или:
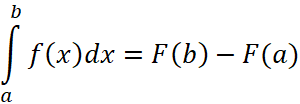 , (27)
, (27)
Эту формулу называют формулой Ньютона-Лейбница или основной формулой интегрального исчисления. Отметим, что если в неопределённом интеграле ![]() указывало на функциональную зависимость первообразной, то в этом случае функциональная зависимость содержится в пределах в пределах интегрирования, например:
указывало на функциональную зависимость первообразной, то в этом случае функциональная зависимость содержится в пределах в пределах интегрирования, например:
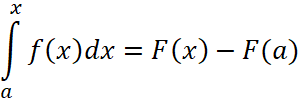 , (28)
, (28)
Установим ряд свойств определённого интеграла, связанных с равенствами:
1. Свойство линейности определённого интеграла:
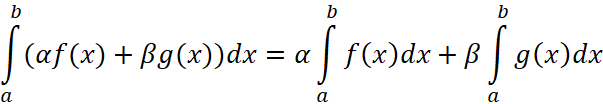 , (29)
, (29)
2.
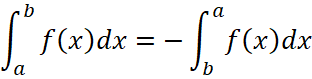 , (30)
, (30)
Заметим, что 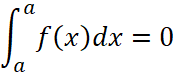 .
.
3.
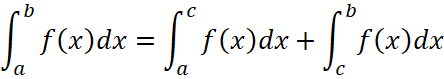 , (31)
, (31)
Эти свойства непосредственно следует из формулы Ньютона-Лейбница.
4. Очевидным образом можно обобщить и формулу интегрирования по частям:
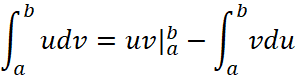 , (32)
, (32)
5. Формула замены переменной интегрирования в определённом интеграле:
Пусть требуется вычислить 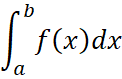 и пусть
и пусть ![]() и не выходит за пределы
и не выходит за пределы ![]() , когда t изменяется в интервале
, когда t изменяется в интервале ![]() , где
, где ![]() и
и ![]() и обе функции удовлетворяют условию (1.2), а функция
и обе функции удовлетворяют условию (1.2), а функция ![]() , где
, где ![]() первообразная
первообразная ![]() , тогда имеет место формула:
, тогда имеет место формула:
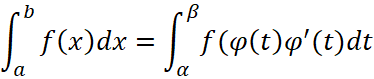 , (33)
, (33)
Доказательство очевидно:
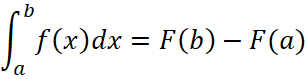 , (34)
, (34)
И
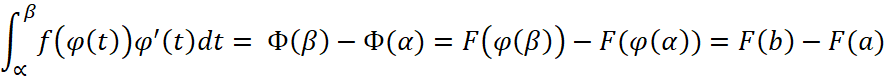 , (35)
, (35)
Установим ряд свойств определённого интеграла, связанных с неравенствами:
1. Пусть ![]() на отрезке
на отрезке ![]() и
и ![]() тогда:
тогда:
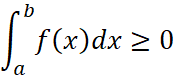 , (36)
, (36)
Доказательство: первообразная 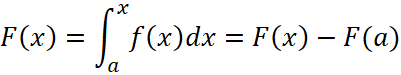 , есть возрастающая функция, поскольку её производная
, есть возрастающая функция, поскольку её производная ![]() неотрицательна и
неотрицательна и ![]() , тогда:
, тогда:
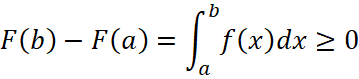 , (37)
, (37)
2. Пусть ![]() на отрезке
на отрезке ![]() и
и ![]() тогда:
тогда:
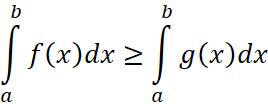 , (38)
, (38)
Доказательство очевидно следует из предыдущего свойства, если его применить к функции ![]() и воспользоваться свойством линейности определённого интеграла.
и воспользоваться свойством линейности определённого интеграла.
3. Ещё одно очевидное свойство:
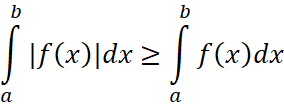 , (39)
, (39)
Справедливость которого следует из (38), поскольку ![]() .
.
В этом параграфе мы продолжили следовать логике параграфа 1: ввели понятие неопределённого интеграла или первообразной функции и её приращение между точками a и b назвали определённым интегралом. Далее мы построим таблицу интегралов для базовых элементарных функций, вычислить интеграл от любой элементарной функции невозможно, поскольку не от всякой элементарной функции интеграл выражается через элементарные функции и к числу таких относятся даже простой на первый взгляд интеграл 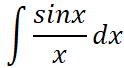 т. н. интегральный синус. Для определенных интегралов имеются способы численного вычисления и поэтому мы первоначально установим его геометрический смысл и укажем один из таких способов, имеющий наглядный смысл.
т. н. интегральный синус. Для определенных интегралов имеются способы численного вычисления и поэтому мы первоначально установим его геометрический смысл и укажем один из таких способов, имеющий наглядный смысл.
По аналогии с параграфом 1, покажем, как отыскать первообразную для функции ![]() . Поскольку мы знаем производную от
. Поскольку мы знаем производную от ![]() , то первообразная
, то первообразная ![]() будет равна:
будет равна:
 , (40)
, (40)
В чем можно убедиться непосредственным дифференцированием.
Геометрическая интерпретация определённого интеграла и его численное вычисление.
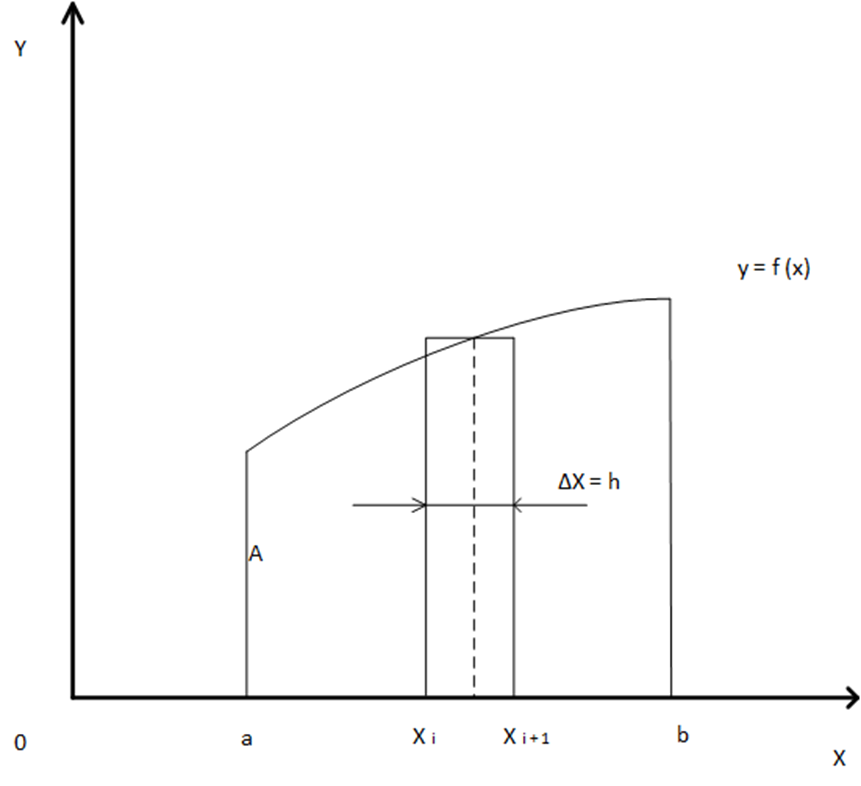
Рис. 2
Проведем разбиение отрезка ![]() на n равных интервалов длиной
на n равных интервалов длиной ![]() , пронумеруем точки разбиения индексом i, который будет изменяться от 0 до n так что
, пронумеруем точки разбиения индексом i, который будет изменяться от 0 до n так что ![]() ,
, ![]() . Выделим интервал
. Выделим интервал ![]() , а на этом интервале его середину
, а на этом интервале его середину 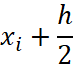 и восстановим из неё перпендикуляр к оси Х до пересечения с графиком функции
и восстановим из неё перпендикуляр к оси Х до пересечения с графиком функции ![]() и построим прямоугольник с вершинами в точках
и построим прямоугольник с вершинами в точках ![]() и сторонами длиной
и сторонами длиной 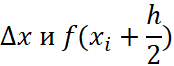 , площадь этого прямоугольника равна
, площадь этого прямоугольника равна 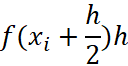 и тогда площадь фигуры (криволинейная трапеция) под графиком функции будет приближённо определятся суммой площадей всех прямоугольников и тем точнее, чем меньше
и тогда площадь фигуры (криволинейная трапеция) под графиком функции будет приближённо определятся суммой площадей всех прямоугольников и тем точнее, чем меньше ![]() , называемую шагом разбиения.
, называемую шагом разбиения.
Выпишем эту сумму:
| (41) |
Представим 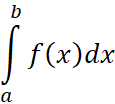 в виде суммы интегралов по промежуткам разбиения, воспользовавшись свойством определённого интеграла (31):
в виде суммы интегралов по промежуткам разбиения, воспользовавшись свойством определённого интеграла (31):
| (42) |
Найдем модуль разности 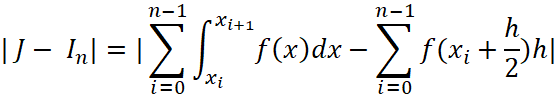 и запишем под одним знаком интеграла воспользовавшись свойством
и запишем под одним знаком интеграла воспользовавшись свойством 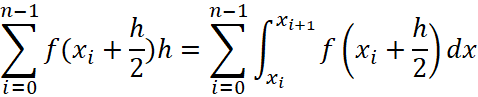 . Таким образом эта разница будет иметь вид:
. Таким образом эта разница будет иметь вид:
| (43) |
И представим функции, на основании нашего основного условия (1.2) в виде:
| (43) |
Тогда под знаком интеграла в сумме останется:
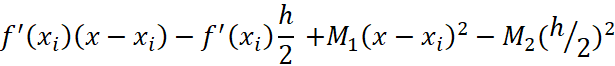 , (44)
, (44)
Вычислим непосредственно интеграл от первых двух членов разности. В первом интеграле 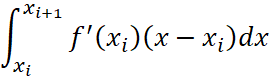 вынесем постоянную
вынесем постоянную ![]() из-под знака интеграла и введем переменную
из-под знака интеграла и введем переменную ![]() , где нижний предел
, где нижний предел ![]() , а верхний предел
, а верхний предел ![]() . Тем самым получим
. Тем самым получим 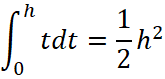 , используя ранее полученный результат вычисления первообразной
, используя ранее полученный результат вычисления первообразной ![]() . Во втором интеграле вынесем постоянную
. Во втором интеграле вынесем постоянную ![]() и получим
и получим 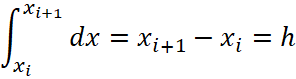 , так что оба интеграла одинаковы и их разность равна нулю. Таким образом:
, так что оба интеграла одинаковы и их разность равна нулю. Таким образом:
| (45) |
Воспользовавшись неравенством ![]() перенесём знак модуля на интеграл:
перенесём знак модуля на интеграл:
| (46) |
Далее усилим это неравенство применив свойство (3) из неравенств для определённого интеграла, перенеся знак модуля под интеграл и ещё усилив, перенесем знак модуля на каждое слагаемое:
| (47) |
Обозначим через 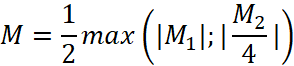 , а
, а ![]() большей величиной
большей величиной ![]() , получим:
, получим:
| (48) |
Т. к. шаг разбиения равен ![]() , то выбором n – количества интервалов разбиения мы можем сделать разность
, то выбором n – количества интервалов разбиения мы можем сделать разность ![]() сколь угодно малой что и доказывает, что
сколь угодно малой что и доказывает, что 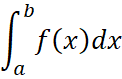 дает площадь криволинейной трапеции, верхнее основание которой представляет график функции
дает площадь криволинейной трапеции, верхнее основание которой представляет график функции ![]() , нижнее ось абсцисс и боковые стороны есть перпендикуляры к этой оси из точек x=a, x=b, что и показано на рисунке 2, а формулу:
, нижнее ось абсцисс и боковые стороны есть перпендикуляры к этой оси из точек x=a, x=b, что и показано на рисунке 2, а формулу:
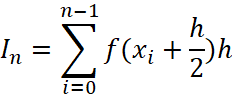 , (49)
, (49)
Принято называть квадратурной формулой прямоугольников, она позволяет численно вычислять определенные интегралы и погрешность этих вычислений имеет величину порядка ![]() . В строгой терминологии принято говорить, что последовательность
. В строгой терминологии принято говорить, что последовательность ![]() сходится к
сходится к 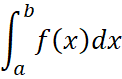 .
.
Общим выводом проведённого рассмотрения является важное правило: если мы имеем дифференциал некоторой величины (в нашем случае это площадь ![]() , что качественно можно увидеть если в выражении для площади выделенного прямоугольника оставить линейные по
, что качественно можно увидеть если в выражении для площади выделенного прямоугольника оставить линейные по ![]() члены), то сама величина получается вычислением определённого интеграла. Также многочисленные применения интегрального исчисления в можно встретить науках, законы в которых сформулированы в виде дифференциальных уравнений, в которых неизвестная функция находится под знаком производной. Один из классов таких уравнений, а именно уравнения с разделяющими переменными
члены), то сама величина получается вычислением определённого интеграла. Также многочисленные применения интегрального исчисления в можно встретить науках, законы в которых сформулированы в виде дифференциальных уравнений, в которых неизвестная функция находится под знаком производной. Один из классов таких уравнений, а именно уравнения с разделяющими переменными 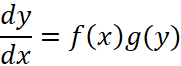 . Переменные x и у можно отделить друг от друга, если умножить обе части уравнения на
. Переменные x и у можно отделить друг от друга, если умножить обе части уравнения на ![]() и поделить на
и поделить на ![]() и тогда получаем выражение, в котором обе части зависят только от своих переменных:
и тогда получаем выражение, в котором обе части зависят только от своих переменных:
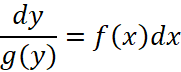 , (50)
, (50)
Интегрируя обе части, получим решение уравнения, оно будет зависеть от произвольной постоянной С, поскольку вычисляется неопределенный интеграл, а если задано начальное условие на функцию в виде ![]() , то можно получить единственное решение в виде неявной функции, записанное как определенный интеграл:
, то можно получить единственное решение в виде неявной функции, записанное как определенный интеграл:
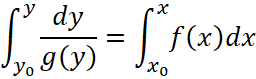 , (51)
, (51)
С многочисленными применениями такого рода уравнений можно ознакомиться в книге Я. Б. Зельдовича и И. М. Яглома «Высшая математика для начинающих физиков и техников».
3. Таблицы производных и интегралов базовых элементарных функций
1. Степенная функция
а) Рассмотрим степенную функцию ![]() , где n натуральное число. Выпишем приращение этой функции
, где n натуральное число. Выпишем приращение этой функции ![]() и выпишем первый член в порядке возрастания степеней ∆x начиная с нулевой, ограничиваясь двумя членами в явном виде
и выпишем первый член в порядке возрастания степеней ∆x начиная с нулевой, ограничиваясь двумя членами в явном виде ![]() , первый член получен от умножения n скобок, если выбираем x в каждой скобке. Второй член содержит множитель n который получается вследствие перемножения n скобок, поскольку в одной из n скобок мы выбираем ∆x, а во всех остальных (n-1) скобках выбираем x. В третий член соберем все оставшиеся члены произведения и
, первый член получен от умножения n скобок, если выбираем x в каждой скобке. Второй член содержит множитель n который получается вследствие перемножения n скобок, поскольку в одной из n скобок мы выбираем ∆x, а во всех остальных (n-1) скобках выбираем x. В третий член соберем все оставшиеся члены произведения и ![]() вынесем отдельно, чем подтвердим условие (1.2):
вынесем отдельно, чем подтвердим условие (1.2):
![]() , (52)
, (52)
Тогда имеем для дифференциала и производной степенной функции, равенства ![]() или
или ![]() справедливые для целого
справедливые для целого ![]() .
.
Выведем формулу для случая корня ![]() или в виде степени
или в виде степени 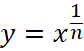 , поскольку корень есть обратная функция к только что рассмотренной, то воспользуемся правилом дифференцирования обратной функции применительно к случаю
, поскольку корень есть обратная функция к только что рассмотренной, то воспользуемся правилом дифференцирования обратной функции применительно к случаю ![]() , тогда обратная к ней функция по определению дается выражением
, тогда обратная к ней функция по определению дается выражением ![]() в котором и будем дифференцировать обе части равенства. Имеем
в котором и будем дифференцировать обе части равенства. Имеем ![]() по правилу дифференцирования сложной функции, отсюда
по правилу дифференцирования сложной функции, отсюда 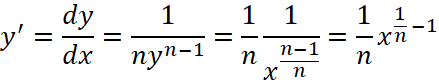 .
.
Для отрицательных степеней такую же формула дифференцирования легко установить если применить правило дифференцирования дроби и таким образом для любых степеней функции ![]() имеем:
имеем:
![]() , (53)
, (53)
Формула первообразной функции ![]() легко установить, если найти производную от
легко установить, если найти производную от ![]() , равную
, равную ![]() с одной стороны и равную
с одной стороны и равную ![]() с другой. Воспользовавшись равенством многочленов
с другой. Воспользовавшись равенством многочленов ![]() , получим
, получим ![]() и
и ![]() , откуда
, откуда ![]() и
и 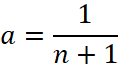 , окончательно получим
, окончательно получим 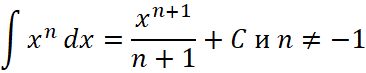 .
.
Поскольку мы умеем находить дифференциал степенной функции, то укажем способ вычисления ![]() с точностью до членов линейных по α и это будет
с точностью до членов линейных по α и это будет ![]() и точность этого приближения дается величиной порядка
и точность этого приближения дается величиной порядка ![]() .
.
2. Тригонометрические функции
Найдем производную функции ![]() , для этого изобразим первый квадрант тригонометрического круга.
, для этого изобразим первый квадрант тригонометрического круга.
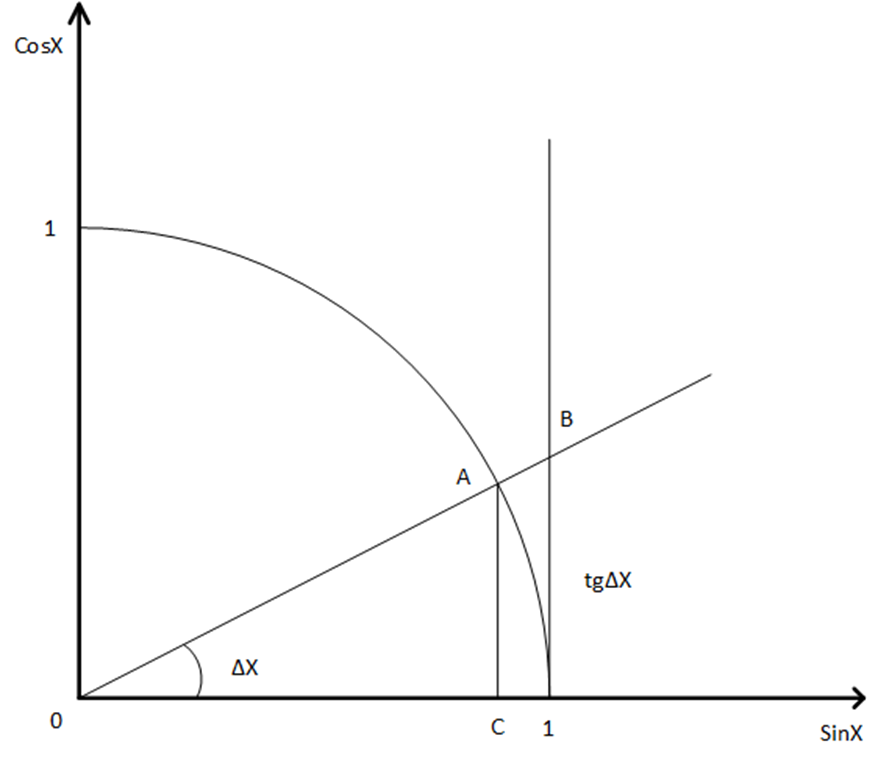
Рис. 3
И выпишем приращение функции ![]() . Будем полагать ∆х малым и оценим величины
. Будем полагать ∆х малым и оценим величины ![]() и
и ![]() с точностью до линейных членов и рассмотрим площади треугольников
с точностью до линейных членов и рассмотрим площади треугольников 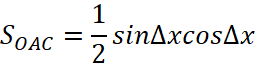 ,
, 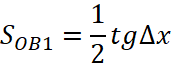 и сектора ОА1
и сектора ОА1 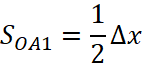 . Очевидно, имеют место неравенства
. Очевидно, имеют место неравенства ![]() .
.
Оставим в выражениях для площадей только линейные по ∆х слагаемые, тогда c требуемой точность имеем:
| (54) |
Тогда наши неравенства мы можем переписать уже в виде нестрогих, поскольку учли только линейные члены и неравенства не теряют смысл т. к. в силу малости ∆х остальными членами можно пренебречь. С учетом сделанных замечаний имеем неравенства:
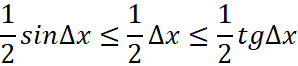 , (55)
, (55)
Что означает эквивалентность ![]() и
и ![]() , с точностью до линейной части по
, с точностью до линейной части по ![]() . Оставляя в приращении только её линейную часть, получаем дифференциал
. Оставляя в приращении только её линейную часть, получаем дифференциал ![]() или для производной
или для производной ![]() .
.
Тогда первообразная от косинуса равна 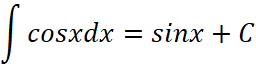 .
.
Найдем производную от функции обратной к ![]() , по определению обратной функции она равна
, по определению обратной функции она равна ![]() , где
, где 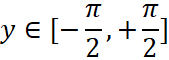 (в привычных обозначениях
(в привычных обозначениях ![]() ). Дифференцируя равенство
). Дифференцируя равенство ![]() , получим
, получим ![]() и найдем
и найдем 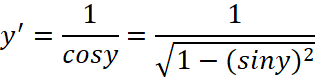 и воспользовавшись тождеством
и воспользовавшись тождеством ![]() получаем
получаем 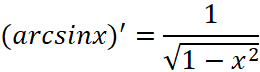 , для первообразной имеем равенство:
, для первообразной имеем равенство:
| (56) |
Для других тригонометрических функций производные можно вычислить, используя их определения и правила дифференцирования. Например, 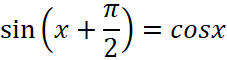 можно дифференцировать, используя правило дифференцирования сложной функции
можно дифференцировать, используя правило дифференцирования сложной функции 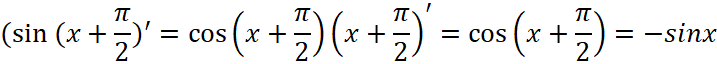 .
.
Получаем правило вычисления производной: ![]() и правило вычисления первообразной
и правило вычисления первообразной 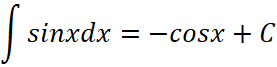 .
.
Для всех других функций можно просто применить правила дифференцирования.
3. Показательная и логарифмическая функции
При рассмотрении функций будем исходить из их определения, основанного на понятии функциональных уравнений. Данный подход подробно изложен в учебнике Г. М. Фихтенгольца «Дифференциальное и интегральное исчисление» т.1 стр. 158. Издание 1997 г. Издательство «Лань».
Показательной функцией ![]() будем называть функцию, удовлетворяющую функциональному уравнению
будем называть функцию, удовлетворяющую функциональному уравнению ![]() , а обратную к ней функцию
, а обратную к ней функцию ![]() или в традиционных обозначениях
или в традиционных обозначениях ![]() , где
, где ![]() удовлетворяет функциональному уравнению
удовлетворяет функциональному уравнению ![]() ,
, ![]() .
.
Убедимся, что введенная функция ![]() , которая называется натуральным логарифмом и задается определённым интегралом с переменным верхним пределом:
, которая называется натуральным логарифмом и задается определённым интегралом с переменным верхним пределом: 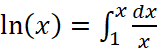 ,
, ![]() .
.
Докажем, что такая функция удовлетворяет функциональному уравнению 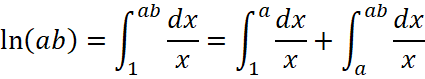 .
.
Мы воспользовались свойством аддитивности (31) определённого интеграла, первый член этой суммы есть 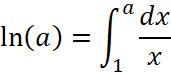 , а во втором выполним подстановку (замену переменной интегрирования x на t)
, а во втором выполним подстановку (замену переменной интегрирования x на t) ![]() ,
, ![]() и нижний предел
и нижний предел 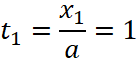 , а верхний предел равен
, а верхний предел равен 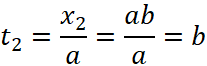 и тем самым получаем функциональное уравнение
и тем самым получаем функциональное уравнение ![]() , для логарифмической функции. Также легко видеть, что и для отрицательных степеней тоже имеется равенство справедливое для логарифмической функции
, для логарифмической функции. Также легко видеть, что и для отрицательных степеней тоже имеется равенство справедливое для логарифмической функции ![]() . Выпишем по определению
. Выпишем по определению 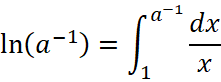 .
.
Выполняя замену подстановку ![]() получим
получим 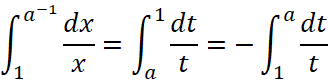 .
.
Основание натурального логарифма называют постоянной Эйлера, обозначают буквой e и численное значение этой постоянной можно определить из уравнения ![]() или в явном виде
или в явном виде 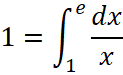 .
.
Это уравнение решается численно по следующему алгоритму: Определим интервал, содержащий корень уравнения, последовательно выбирая в качестве верхнего предела числа 2,3…, найдем интервал корня ![]() и далее выполняя деление этого отрезка пополам найдем новый интервал корня, повторяем эту процедуру до той поры пока не достигнем требуемой точности вычисления корня уравнения и при этом необходимо согласовать точность вычисления интеграла с точностью вычисления корня.
и далее выполняя деление этого отрезка пополам найдем новый интервал корня, повторяем эту процедуру до той поры пока не достигнем требуемой точности вычисления корня уравнения и при этом необходимо согласовать точность вычисления интеграла с точностью вычисления корня.
Покажем, что обратная функция натурального логарифма 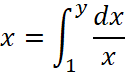 или показательная функция
или показательная функция ![]() , удовлетворяет соответствующему функциональному уравнению
, удовлетворяет соответствующему функциональному уравнению ![]() . Имеем
. Имеем 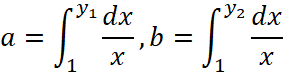 и
и ![]() , тогда
, тогда 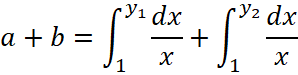 . В первом интеграле выполним замену переменной интегрирования
. В первом интеграле выполним замену переменной интегрирования ![]() , тогда
, тогда 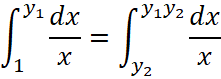 и воспользовавшись свойством аддитивности определённого интеграла получим
и воспользовавшись свойством аддитивности определённого интеграла получим 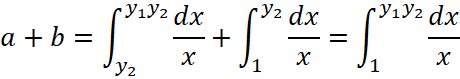 . Тем самым доказано, что функция
. Тем самым доказано, что функция ![]() удовлетворяет функциональному уравнению для показательной функции и её основанием является постоянная Эйлера (подтверждение численный расчет) и эту функцию называют экспонентой, а функциональную зависимость экспоненциальной.
удовлетворяет функциональному уравнению для показательной функции и её основанием является постоянная Эйлера (подтверждение численный расчет) и эту функцию называют экспонентой, а функциональную зависимость экспоненциальной.
Отыскание производной функции натурального логарифма вытекает из её определения 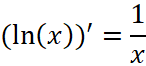 .
.
Производную от экспоненты можно найти из её определения 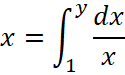 , если взять производную от обеих частей равенства
, если взять производную от обеих частей равенства 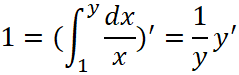 . Мы воспользовались правилом дифференцирования сложной функции, т. е. интеграл продифференцировали по переменной
. Мы воспользовались правилом дифференцирования сложной функции, т. е. интеграл продифференцировали по переменной ![]() и умножили на производную этой функции по переменной x. Умножая обе части полученного выражения на
и умножили на производную этой функции по переменной x. Умножая обе части полученного выражения на ![]() получим
получим ![]() или факт, что экспонента при дифференцировании и интегрировании не меняет функциональной зависимости.
или факт, что экспонента при дифференцировании и интегрировании не меняет функциональной зависимости.
Правило дифференцирования показательной функции вида ![]() и логарифмической функции вида
и логарифмической функции вида ![]() легко получить имея в виду формулы
легко получить имея в виду формулы ![]() и
и 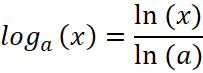 .
.
Дополнение
Мы рассмотрели обоснование аппарата математического анализа, который на уровне рецептуры предлагается в современном школьном курсе математики. Есть ряд важных понятий и связанных с ними свойствами функций, которые следует рассмотреть, поскольку они фактически являются фундаментом мат. анализа и позволят установить условия применимости предлагаемого подхода. Одним из таких понятий является непрерывность функции в точке.
Определение:
Функцию ![]() будем называть непрерывной в точке
будем называть непрерывной в точке ![]() , если для любого сколь угодно малого
, если для любого сколь угодно малого ![]() найдется такое
найдется такое ![]() , что неравенство
, что неравенство ![]() будет выполняться для всех удовлетворяющих неравенству
будет выполняться для всех удовлетворяющих неравенству ![]() (дельта окрестность точки
(дельта окрестность точки ![]() ).
).
Функцию непрерывную в каждой точке отрезка ![]() будем называть непрерывной на отрезке.
будем называть непрерывной на отрезке.
Рассмотрим основное условие, которым мы пользовались при выделении класса рассматриваемых функций:
![]() , (57)
, (57)
И покажем, что такие функции являются непрерывными в силу выполнения неравенства:
![]() , (58)
, (58)
Выберем дельта окрестность точки ![]() достаточно малой, чтобы можно было пренебречь вторым слагаемым (случай
достаточно малой, чтобы можно было пренебречь вторым слагаемым (случай ![]() ) в виде
) в виде 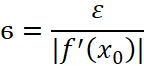 и, тогда как только
и, тогда как только ![]() неравенство выполняется. Для случая
неравенство выполняется. Для случая ![]() в качестве дельта можно выбрать
в качестве дельта можно выбрать 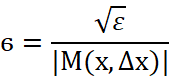 и неравенство будет справедливо для всех
и неравенство будет справедливо для всех ![]() .
.
Докажем важную теорему о свойстве непрерывной функции:
Первая теорема Больцано-Коши:
Пусть непрерывная на отрезке ![]() функция
функция ![]() принимает на его границах значения разных знаков
принимает на его границах значения разных знаков ![]() . Тогда внутри отрезка найдется по крайней мере одна точка α, в которой
. Тогда внутри отрезка найдется по крайней мере одна точка α, в которой ![]() .
.
Доказательство:
Сформулируем алгоритм поиска такой точки, который носит название метода половинного деления. Делим отрезок ![]() пополам и обозначим координату средины отрезка через
пополам и обозначим координату средины отрезка через ![]() , в этой точке функция может принимать значения
, в этой точке функция может принимать значения ![]() , первое из этих значений мы не будем рассматривать поскольку оно доказывает теорему. Два других значения позволяют выбрать из двух половинок новый отрезок с граничной точкой
, первое из этих значений мы не будем рассматривать поскольку оно доказывает теорему. Два других значения позволяют выбрать из двух половинок новый отрезок с граничной точкой ![]() , на концах которого функция
, на концах которого функция ![]() принимает значения разных знаков. Повторяя эту процедуру, мы придем к некоторому действительному числу α, в полном соответствии со свойством плотности множества действительных чисел. Рассмотрим ситуацию на n-шаге, длина интервала равна
принимает значения разных знаков. Повторяя эту процедуру, мы придем к некоторому действительному числу α, в полном соответствии со свойством плотности множества действительных чисел. Рассмотрим ситуацию на n-шаге, длина интервала равна 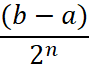 и будет сколь угодно малой с ростом n. Рассмотрим также последовательности границ интервалов
и будет сколь угодно малой с ростом n. Рассмотрим также последовательности границ интервалов ![]() и
и ![]() которые составлены таким образом, что
которые составлены таким образом, что ![]() , а
, а ![]() . Эти границы с ростом n будут приближаться к числу α, поскольку всегда можно выбрать длину интервала сколь угодно малой. Последовательности значений функции
. Эти границы с ростом n будут приближаться к числу α, поскольку всегда можно выбрать длину интервала сколь угодно малой. Последовательности значений функции ![]() и
и ![]() будут приближённо задавать значение
будут приближённо задавать значение ![]() с точностью равной длине интервала, в силу положительности
с точностью равной длине интервала, в силу положительности ![]() одной и отрицательности другой членов последовательностей
одной и отрицательности другой членов последовательностей ![]() , получим единственную возможность
, получим единственную возможность ![]() .
.
Прямым следствием этой теоремы является теорема о промежуточных значениях непрерывной функции:
Вторая теорема Больцано-Коши:
Пусть функция ![]() определена и непрерывна на некотором промежутке и если в двух точках a и b (
определена и непрерывна на некотором промежутке и если в двух точках a и b (![]() ) этого промежутка, принимает неравные значения
) этого промежутка, принимает неравные значения ![]() , то для любого значения, С удовлетворяющего неравенству
, то для любого значения, С удовлетворяющего неравенству ![]() (для определённости, будем полагать
(для определённости, будем полагать ![]() ) найдётся такая точка с
) найдётся такая точка с ![]() , что
, что ![]() .
.
Доказательство:
Доказательство вполне очевидно, если рассмотреть функцию ![]() и она на концах отрезка
и она на концах отрезка ![]() принимает значение разных знаков, следовательно из результатов предыдущей теоремы обращается в ноль в некоторой точке, что и доказывает теорему.
принимает значение разных знаков, следовательно из результатов предыдущей теоремы обращается в ноль в некоторой точке, что и доказывает теорему.
В основе многих теорем и формул дифференциального исчисления и его приложений лежит важная теорема, которую связывают с именем Ролля.
Теорема Ролля
Пусть функция ![]() определена и непрерывна на отрезке
определена и непрерывна на отрезке ![]() и существует конечная производная
и существует конечная производная ![]() на этом отрезке, а на концах этого отрезка функция принимает равные значения
на этом отрезке, а на концах этого отрезка функция принимает равные значения ![]() , тогда между точками а и в найдется точка с в которой производная обращается в ноль.
, тогда между точками а и в найдется точка с в которой производная обращается в ноль.
Доказательство:
Для доказательства мы усилим требования на производную функции ![]() и будем считать её непрерывной, для наших целей это предположение оправдано, поскольку справедливо для класса рассматриваемых функций. Найдём на отрезке
и будем считать её непрерывной, для наших целей это предположение оправдано, поскольку справедливо для класса рассматриваемых функций. Найдём на отрезке ![]() точку
точку ![]() в которой
в которой ![]() и
и ![]() и в этой точке функция будет возрастать. Поскольку функция на концах отрезка принимает равные значения, то найдётся точка
и в этой точке функция будет возрастать. Поскольку функция на концах отрезка принимает равные значения, то найдётся точка ![]() в которой
в которой ![]() и функция будет убывать. Таким образом на отрезке
и функция будет убывать. Таким образом на отрезке ![]() , для производной выполняются условия теоремы Больцано-Коши, что и доказывает эту теорему.
, для производной выполняются условия теоремы Больцано-Коши, что и доказывает эту теорему.
Полезной для теоретических рассмотрений также является теорема Лагранжа или формула конечных приращений.
Теорема Лагранжа
Пусть ![]() определена и непрерывна на отрезке и на этом отрезке существует производная
определена и непрерывна на отрезке и на этом отрезке существует производная ![]() . Тогда в этом промежутке отыщется точка с для которой будет иметь место равенство
. Тогда в этом промежутке отыщется точка с для которой будет иметь место равенство 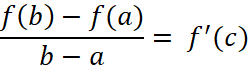 .
.
Доказательство:
Введём вспомогательную функцию на этом промежутке 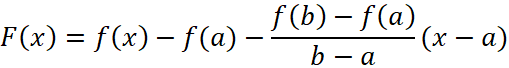 .
.
Эта функция удовлетворяет условиям теоремы Ролля, тогда найдется точка с в которой производная обращается в ноль 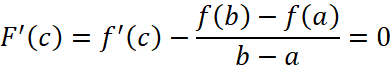 , что и представляет формулу конечных приращений.
, что и представляет формулу конечных приращений.
Геометрический смысл этой формулы прозрачен, поскольку 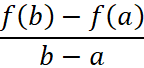 угловой коэффициент секущей, которая проходит через точки
угловой коэффициент секущей, которая проходит через точки ![]() , а
, а ![]() угловой коэффициент касательной, проходящей через точку
угловой коэффициент касательной, проходящей через точку ![]() , то равенство угловых коэффициентов означает параллельность секущей и касательной.
, то равенство угловых коэффициентов означает параллельность секущей и касательной.
Прямым следствием теоремы Лагранжа является теорема о среднем значении определённого интеграла.
Теорема о среднем значении определённого интеграла
Пусть ![]() определена и непрерывна на отрезке
определена и непрерывна на отрезке ![]() и существует определённый интеграл
и существует определённый интеграл 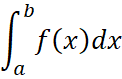 , тогда в этом промежутке отыщется точка с для которой будет иметь место равенство:
, тогда в этом промежутке отыщется точка с для которой будет иметь место равенство:
| (59) |
Доказательство:
По формуле Ньютона-Лейбница имеем 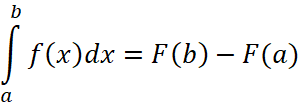 , а по теореме Лагранжа получим
, а по теореме Лагранжа получим ![]() , что и доказывает теорему о среднем значении.
, что и доказывает теорему о среднем значении.
Мы сейчас установим достаточные условия на класс рассматриваемых функций, которые удовлетворяют условию (1.2). Заметим, что ![]() тоже является функцией и мы можем вычислить её производную и она называется производной второго порядка или просто второй производной функции
тоже является функцией и мы можем вычислить её производную и она называется производной второго порядка или просто второй производной функции ![]() и обозначается как
и обозначается как ![]() . Рассмотрим функцию
. Рассмотрим функцию ![]() и воспользуемся дважды теоремой Лагранжа
и воспользуемся дважды теоремой Лагранжа 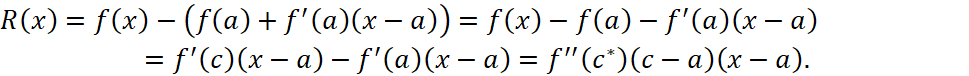
Введя обозначение ![]() , где
, где ![]() получим
получим ![]() что и доказывает утверждение:
что и доказывает утверждение:
Достаточным условием для того, чтобы функция удовлетворяла условию (1.2) является существование ограниченной второй производной функции в рассматриваемом интервале.
Задания для самостоятельного решения
Приведём, в данном разделе, небольшое количество задач, чтобы прояснить темы задания действительных чисел последовательностями и качественные аспекты применения понятия дифференциала, которые легко могут быть строго доказаны. Для полного изучения всех этих разделов имеется много прекрасных сборников задач: трёхтомник «Сборник задач по высшей математике» авторы Н. М. Гюнтер и Р. О. Кузьмин, охватывающий все рассмотренные в пособии темы или Б. П. Демидович «Сборник задач и упражнений по математическому анализу», также для закрепления темы дифференциальных уравнений с разделяющими переменными книгу Филиппов А. Ф. «Сборник задач по дифференциальным уравнениям». Многочисленные примеры применения изложенного аппарата имеются в книге Я. Б. Зельдовича и И. М. Яглома «Высшая математика для начинающих физиков и техников».
1. Пусть период бесконечной дроби содержит m цифр ![]() получить соответствующее ему рациональное число
получить соответствующее ему рациональное число ![]() .
.
Указание: выписать сумму N членов разложения по степеням десяти, вынести за скобки период и просуммировать полученную геометрическую прогрессию и убедиться, что слагаемое, зависящее от N задаёт приближение к числу ноль.
2. Доказать, что сумма и произведение рационального с иррациональным числами, будет иррациональным числом.
3. Доказать, что последовательность 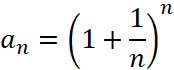 является приближением (имеет пределом) основание натуральных логарифмов.
является приближением (имеет пределом) основание натуральных логарифмов.
Указание: рассмотреть последовательность ![]() , воспользовавшись формулой (1.2), в которой оставить главный член.
, воспользовавшись формулой (1.2), в которой оставить главный член.
4. Доказать неравенство Бернулли ![]() , при
, при ![]() .
.
5. Доказать, что последовательность 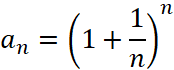 монотонно возрастающая (
монотонно возрастающая (![]() ).
).
Указание: рассмотреть 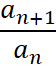 и доказать, что
и доказать, что 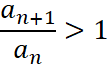 , воспользовавшись неравенством Бернулли.
, воспользовавшись неравенством Бернулли.
6. Доказать, что последовательность 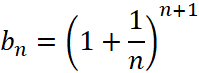 монотонно убывающая (
монотонно убывающая (![]() ).
).
Указание: рассмотреть 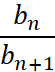 и доказать, что
и доказать, что 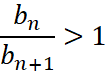 , воспользовавшись неравенством Бернулли.
, воспользовавшись неравенством Бернулли.
7. Доказать, что последовательность ![]() из задачи 5, является приближением к основанию натуральных логарифмов снизу
из задачи 5, является приближением к основанию натуральных логарифмов снизу ![]() , а последовательность
, а последовательность ![]() , приближение сверху и
, приближение сверху и ![]() на этом основании оценить погрешность вычисления числа e.
на этом основании оценить погрешность вычисления числа e.
8. Получить формулу вычисления объёма тела вращения относительно оси ОХ ![]() кривой между точками
кривой между точками ![]() и
и ![]() .
.
Указание: рассмотреть вращение кривой на рисунке 2 и получить объём элементарного цилиндра, полученного от вращения прямоугольника 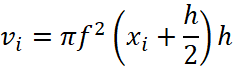 и просуммировав объёмы таких цилиндров получим последовательность
и просуммировав объёмы таких цилиндров получим последовательность ![]() , которая будет сходиться к объёму тела вращения и тем самым покажем, что дифференциал объёма
, которая будет сходиться к объёму тела вращения и тем самым покажем, что дифференциал объёма ![]() .
.
9. Определить объём конуса, полученного от вращения кривой ![]() между точками на оси ОХ
между точками на оси ОХ ![]() и
и ![]() и между точками на оси ОХ
и между точками на оси ОХ ![]() и
и ![]() .
.
10. Пусть тело располагается вдоль оси ОZ между двумя параллельными плоскостями z=a и z=b, также известна зависимость площади сечения тела плоскость от z координаты S=S(z). Доказать, что объём тела даёт выражение 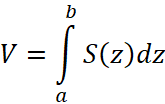 (вычисление объёма тела по площади параллельных сечений).
(вычисление объёма тела по площади параллельных сечений).
11. Вычислить объём треугольной пирамиды с площадью основания S и высотой H.
Указание: воспользоваться формулой объёма из задачи 10, а зависимость площади сечения пирамиды плоскостью. Определить, пользуясь подобием треугольников в сечении пирамиды плоскостью параллельной основанию пирамиды.
12. Эмпирическая формула для скорости истечения жидкости из сосуда ![]() , где с – эмпирический коэффициент, g – ускорение свободного падения, h – высота уровня жидкости. За какое время опорожнится цилиндрическая бочка диаметром D, через отверстие в днище бочки диаметром d.
, где с – эмпирический коэффициент, g – ускорение свободного падения, h – высота уровня жидкости. За какое время опорожнится цилиндрическая бочка диаметром D, через отверстие в днище бочки диаметром d.
Указание: составить уравнение баланса жидкости в сосуде, за время ![]() вытекло из нижнего отверстия
вытекло из нижнего отверстия 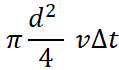 , в бочке
, в бочке 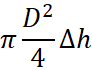 . Считая
. Считая ![]() достаточно малым получить дифференциальное уравнение.
достаточно малым получить дифференциальное уравнение.
13. Установить закон радиоактивного распада, если считать, что скорость распада пропорциональна количеству радиоактивного вещества. Выразить результат через время полураспада (время, за которое распадается половина вещества).
Указание: учесть, что количество вещества уменьшается в процессе распада.
14. Материальная точка массы m падает под действием силы тяжести в среде, где её сопротивление задаётся силой с законом ![]() (k коэффициент, v скорость точки, n натуральное число). Определить закон изменения скорости и путь, пройденный точкой за время T, для n=1 и n=2.
(k коэффициент, v скорость точки, n натуральное число). Определить закон изменения скорости и путь, пройденный точкой за время T, для n=1 и n=2.
.png&w=384&q=75)
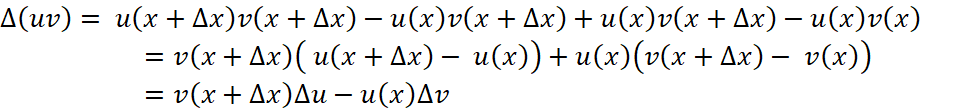
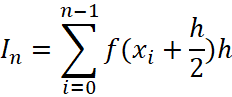
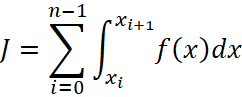
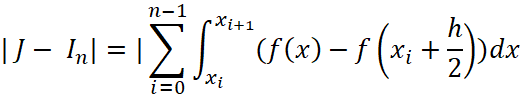
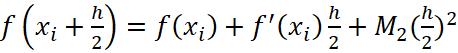
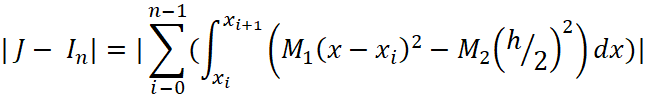
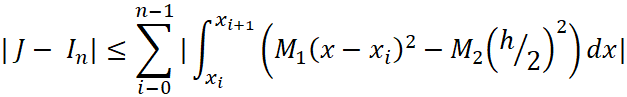
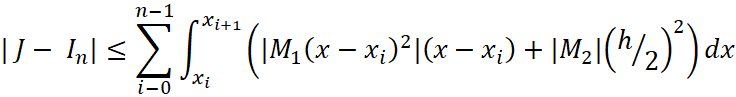
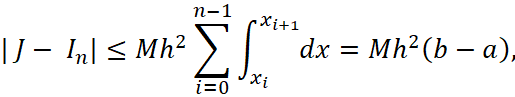
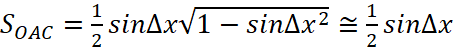 ,
,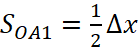 ,
,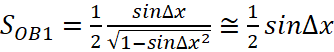 ,
,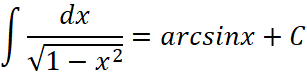
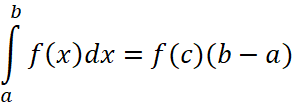
.png&w=640&q=75)