Нечеткая функционально-сетевая модель планирования

В настоящее время развитие интеллектуальных систем управления и принятия решений позволяет использовать их для решения различных задач, включая задачи, связанные с оптимизацией, планированием и прогнозированием [1].

В настоящей работе рассматривается подход к применению принципов нечеткой математики к решению задачи планирования процессов.

В рассматриваемых в [2, 3] моделях планирования временные показатели представлены только в треугольной форме, что ограничивает функционал подобного рода систем. Поэтому в качестве модели планирования предлагается использовать нечёткую функционально-сетевую модель (НФСМ), в которой временные показатели представлены в виде нечётких чисел треугольного и трапециевидного вида.

Для расчёта показателей НФСМ предлагается использовать наборы арифметических операций с временными показателями сетевой модели, сводящиеся к операциям над интервалами соответствующего α-уровня (рис. 1).

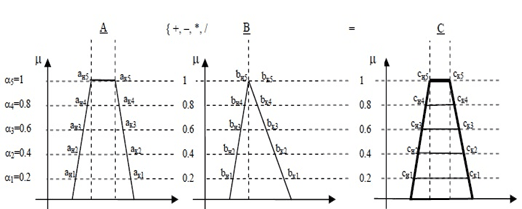
Рис. 1. Пример реализации операции

Одним из основных показателей сетевой модели планирования является продолжительность путей выполнения работ (длина пути), расчет которых в нечетком виде производится по формуле 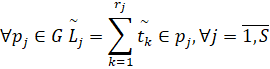(1)

    (1)

где S – количество путей графа;

 – нечёткая продолжительность j-го пути;

 – нечёткое время выполнения k-й работы.

Для анализа продолжительностей путей сетевого графа определяется вектор вида

L={},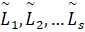

каждый элемент которого определяется исходя из выражения (1), которое при реализации операции разложения по уровням преобразуется в 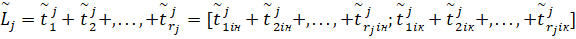(2).

, (2)

,

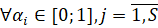где 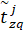 – нечёткая продолжительность k-й работы пути L_k,

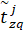 – начало интервала для нечёткого числа  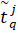при разложении на q-м уровне,

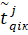 – конец интервала для нечёткого числа  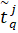при разложении на q-м уровне.

Поиск критического пути в сетевой модели планирования (G) осуществляется путём сравнения нечётких продолжительных осей 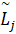 и выбора пути с максимальной 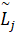(max{}).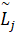

Далее, для всех путей графа планирования находятся резервы времени, относительно критического пути.

Так нечёткий резерв для j-го пути графа G, не совпадающего с критическим определяется исходя из выражения:

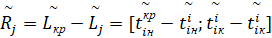
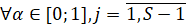  .    (3)

Степень загрузки работ (показатель оптимальности распределения работ) НФСМ определяется исходя из расчета коэффициентов напряженностей (КН) работ графа планирования:

,

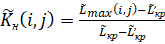где j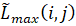 – сумма весов дуг максимального пути, проходящего через работу (i,j);  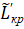– нечеткая сумма весов дуг максимального пути, совпадающих с критическим путём;  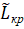– продолжительность критического пути.

Распределение дефаззифицированных КН по группам «резервная», «промежуточная», «критическая» позволяет определить степень оптимальности построения плана.

Рассмотрим пример планирования процесса поставки, представленного в совокупности следующих работ: работа (1,2) – «получение заявки»; работа (1,3) – «составление договора на поставку»; работа (2,4) – «расчет затрат»; работа (2,5) – «формирование заказа»; работа (6,7) – «транспортировка».

НФСМ планируемого процесса представлена на рис. 1.

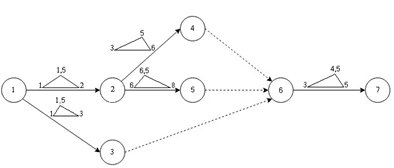
Рис. 1. НФСМ планирования

Выполнена программная реализация процесса планирования на основе НФСМ, позволяющая автоматизировать процесс расчета и оптимизации плана.

На рис. 2 представлена экранная форма задания таблицы связанности графа, которая отражает не только связь вершин, но и показывает продолжительность выполнения работ, заданную в нечетком виде.

Рис. 3 отражает реализацию процесса расчета сетевого графа.

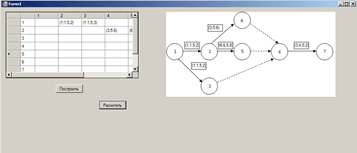
Рис. 2. Экранная форма «Задание исходных данных»

Рис. 3. Экранная форма «Расчет параметров»

Следует отметить, что вывод показателей производится в нечетком виде, а оцениваемый коэффициент напряженности представляется дополнительно и в четком виде, определенном по средствам расчета центра масс нечеткого параметра.