При эксплуатации узлов широкого круга инженерных устройств (двигатели внутреннего сгорания, автоматика роторных и роторно-конвейерных линий, стрелково-пушечного вооружения и др.) поверхности сопрягаемых деталей в процессе эксплуатации подвергаются циклическому ударному нагружению, параметры которого, как правило, не выводят интегральные объемы материалов сопрягаемых деталей из упругого состояния, но при этом ближайшие окрестности контактирующих поверхностей подвергаются локальному неупругому деформированию, в результате чего их геометрические параметры и механические свойства материалов в окрестностях контактирующих поверхностей в процессе эксплуатации необратимо меняются, и формируется отличная от первоначальной топография контактных поверхностей с равновесной микрогеометрией (так называемое явление контактной приработки) – и это необходимо учитывать и закладывать в конструкцию априори на этапах проектирования и отработки. Существует много как конструктивных, так и технологических способов улучшения эксплуатационных характеристик деталей, направленных на целевое планирование комплекса свойств контактирующих поверхностей, формирующих, как правило, в их окрестностях внутренние напряжения противоположного по отношению к возникающим в процессе их эксплуатации знака и тем самым повышающим усталостную прочность деталей и уменьшающим длительность периода приработки [1, с. 186].
Рассматриваемый иррегулярный микрорельеф моделируется группой из пяти консольно защемленных стержней разной высоты и площади поперечного сечения, расположенных на поверхности с определенным шагом, подверженных на концах динамическому сжимающему воздействию (рис. 1). Причем, материалы балок и заделки полностью идентичны, поэтому при их ударном нагружении не будет наблюдаться отражения волн напряжений в месте перехода микронеровностей в объем детали и, как следствие, не будет интерференции волн напряжений, что существенно упрощает задачу [2, с. 33].
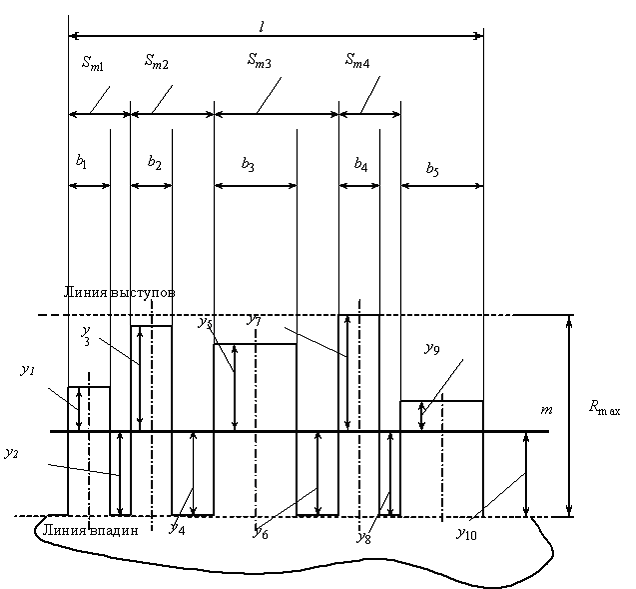
Рис. 1. Модель поверхности с иррегулярной микрогеометрией
Математическая модель, описывающая изменение геометрических параметров микронеровностей в процессе циклического ударного нагружения, представляет собой систему одиннадцати дифференциальных уравнений в частных производных гиперболического типа с начальными и граничными условиями для них, соответствующими задаче Гурса:
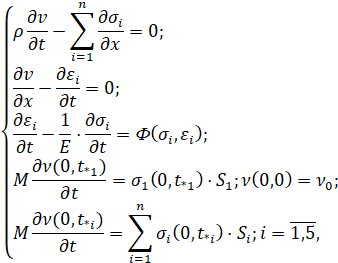 (1)
(1)
где σi, εi, vi – напряжение, полная деформация и скорость в материале микронеровностей соответственно; ρ,E – плотность и модуль упругости материала микронеровностей; M,v0 – ударяющая масса и скорость удара; Si – площадь поперечного сечения микронеровности; x – лагранжева координата; t*i – время вступления в приработку i микронеровности; Ф(σi,εi) – экспериментально определяемая функция, характеризующая комплекс вязкопластических свойств материала микронеровности.
Расчеты проводились численно методом характеристик с конечно-разностной аппроксимацией частных производных вдоль характеристических направлений и с организацией цикла итераций на каждом шаге численного интегрирования с использованием разработанного программного комплекса [3] для двух материалов (алюминий и медь М2) с исходными данными, приведенными в таблице.
Входящие в структуру конституционных уравнений функции Ф(σi,εi), моделирующие комплекс упруго-вязкопластических свойств для выбранных материалов имеют вид [4, с. 25]:
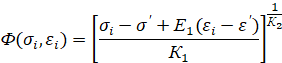 (2)
(2)
где: для меди М2 σ' = 285 МПа; ε'= 0,02; E1 = 500 МПа; K1 = 0,00985; K2 = 0,97; для алюминия σ' = 76 МПа; ε'= 0,005; E1 = 82 МПа; K1 = 2; K2=0,4.
Таблица
Исходные данные
|
Масса |
Скорость удара Vo, м/с |
Геометрические параметры |
Геометрические параметры микронеровностей | ||||||
|
I |
II |
III |
IV |
V | |||||
|
Алюминий | |||||||||
|
0,2 |
31,22 |
Высота, мм |
0,153 |
0,147 |
0,145 |
0,145 |
0,144 | ||
|
Площадь поперечного сечения, мм2 |
1,05 |
1 |
1 |
0,965 |
0,997 | ||||
|
Медь М2 | |||||||||
|
0,2 |
41,22 |
Высота, мм |
0,118 |
0,117 |
0,116 |
0,115 |
0,114 | ||
|
Площадь поперечного сечения, мм2 |
1 |
0,998 |
0,895 |
0,785 |
0,996 | ||||
На рис. 2-3 представлены расчеты изменения высоты микронеровностей в процессе приработки, номер кривой соответствует порядковому номеру микронеровности, вступившей в приработку.
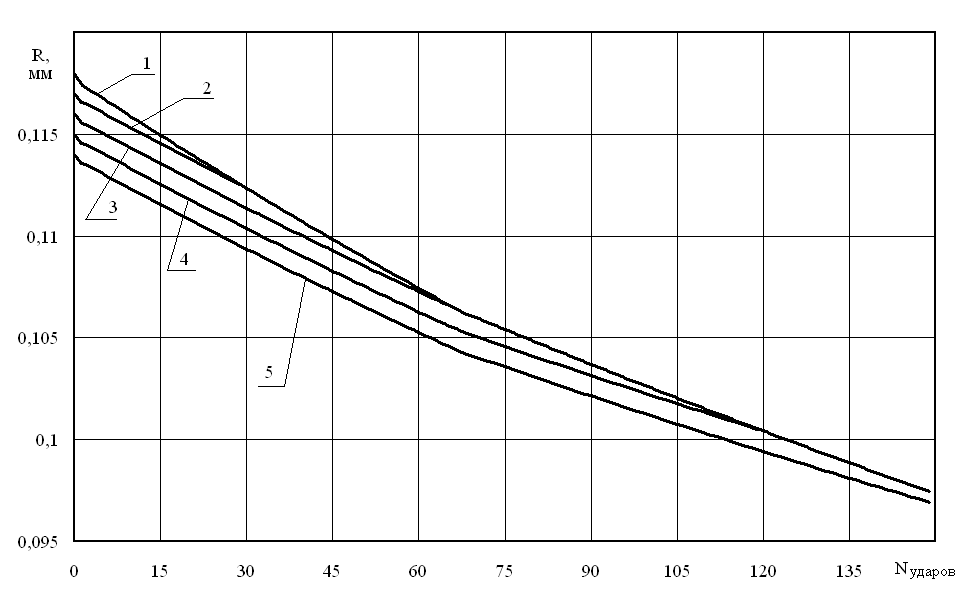
Рис. 2. Изменение высоты микронеровностей (медь 2)
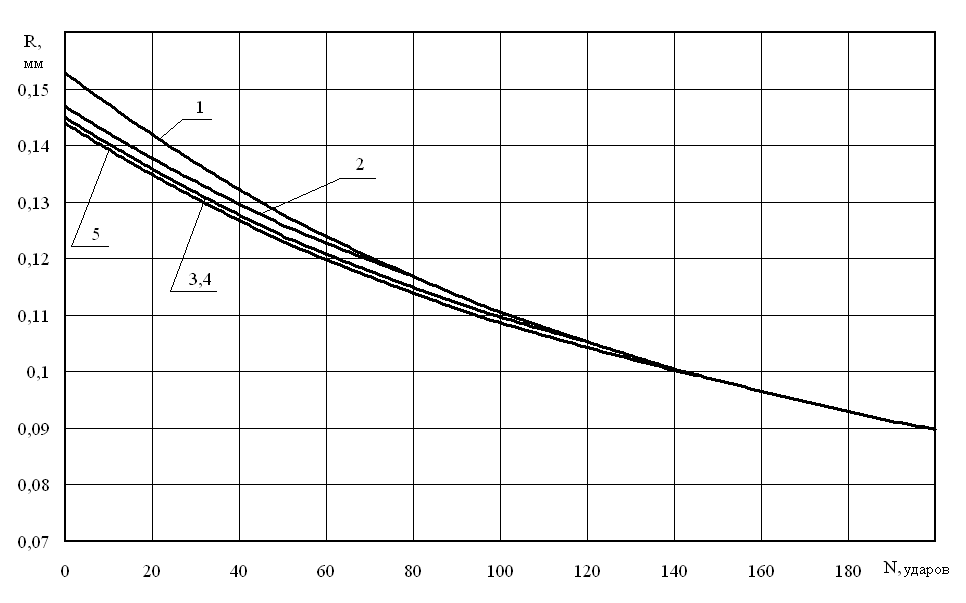
Рис. 3. Изменение высоты микронеровностей (алюминий)
На рис. 2-3 представлены расчеты изменения высоты микронеровностей в процессе приработки, номер кривой соответствует порядковому номеру микронеровности, вступившей в приработку.
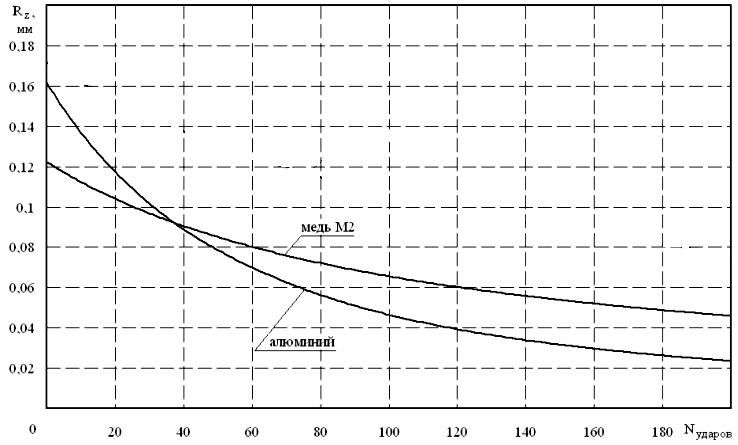
Рис. 4. Изменение Rz в процессе приработки
На рис. 4 показано изменение параметра Rz для двух материалов. Данный график отражает зависимость изменения параметра Rz от свойств материала. Из рис. 4 видно, что у более пластичного материала (алюминия) параметр Rz изменяется интенсивней.
Анализируя полученные результаты, можно сделать вывод о том, что возможны две принципиально различные схемы формирования равновесной геометрии микронеровностей на этапе их приработки: 1) "частичная равновесная приработка", когда микронеровности после приработки не достигают одинаковой высоты (рис. 2); 2) "полная равновесная приработка", когда после приработки все микронеровности имеют одинаковую высоту (рис. 3). Безусловно, второй вариант равновесной приработки является предпочтительным, что позволяет в перспективе сформулировать и реализовать обратную задачу оптимального проектирования начальной микрогеометрии поверхностных микронеровностей с привлечением статистических законов распределения начальных высот микронеровностей и связанных с ними технологическими способами их получения.

.png&w=640&q=75)