При изучении закономерностей образования упаковок из различных минеральных наполнителей со средним размером зерен от нескольких десятков нанометров [1] до миллиметра [2, 3], на основании анализа большого массива экспериментальных данных, нами было показано [4, с. 26-32], что, в основном, попытки уплотнения исходной крупной фракции материала добавлением наполнителей более мелких фракций приводят к снижению плотности упаковки смеси, в сравнении с упаковкой исходного, уже уплотненного наполнителя. При этом общий объём смеси всегда возрастает. Рост объёма как сухой, так и увлажнённой (со смоченными и диспергированными в водной среде зёрнами наполнителей) [5, с. 42-50] упаковки происходит по линейной зависимости согласно уравнению:
![]() , (1)
, (1)
Здесь: ![]() – объём уплотненного наполнителя исходной фракции,
– объём уплотненного наполнителя исходной фракции,
![]() – приращение объема упаковки в результате добавления мелкой фракции,
– приращение объема упаковки в результате добавления мелкой фракции,
![]() – масса крупной и мелкой фракций,
– масса крупной и мелкой фракций,
![]() – плотность смеси;
– плотность смеси;
![]() – объем уплотненной смеси.
– объем уплотненной смеси.
![]() – коэффициент.
– коэффициент.
Коэффициент ![]() тангенс угла наклона прямой, характеризует степень роста объёма смеси при добавлении к ней мелкой фракции.
тангенс угла наклона прямой, характеризует степень роста объёма смеси при добавлении к ней мелкой фракции.
Соответственно, для расчета плотности упаковки ![]() смеси двух наполнителей в их различном соотношении, можно применить [6, с. 38-43] формулу:
смеси двух наполнителей в их различном соотношении, можно применить [6, с. 38-43] формулу:
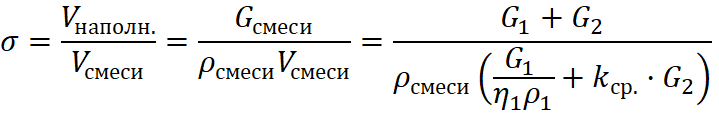 , (2)
, (2)
Здесь ![]() – истинный объём наполнителя в смеси.
– истинный объём наполнителя в смеси.
Если смесь будет состоять из наполнителей различной плотности, то плотность смеси ![]() может быть рассчитана пропорционально массовым долям этих наполнителей:
может быть рассчитана пропорционально массовым долям этих наполнителей:
![]() , (3)
, (3)
Тогда, подставляя выражение (3) в формулу (2) получим:
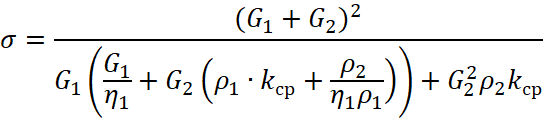 , (4)
, (4)
Где: ![]() – плотность компонента первой крупной фракции,
– плотность компонента первой крупной фракции, ![]() – плотность компонента второй добавляемой фракции.
– плотность компонента второй добавляемой фракции.
Расчёт плотности упаковки материала важен в ряде отраслей промышленности, например, в производстве бетонов, композиционных и лакокрасочных материалов.
Цель проводимых в этом направлении многочисленных исследований [7, с. 53-60; 8, с. 55-60; 9, с. 28-38; 10, с. 15-18; 11, с. 32-35] различных смесей и систем, предложение ряда математических моделей, состояла в поиске таких комбинаций компонентов по форме и диаметрам частиц, при которых происходило бы максимальное уплотнение упаковок, с приданием материалам улучшенных прочностных свойств.
При производстве бетонов заполнители и наполнители с размером частиц от долей миллиметра до десятков миллиметров, являются компонентами, формирующими объемную структуру бетона. Они позволяют сократить расход цемента, увеличить прочность и модуль деформации бетона. Эффективность гранулометрического состава зернистого компонента предусматривает обеспечение наибольшей плотности упаковки его частиц, требуемой удельной поверхности при необходимом числе фракций в полидисперсной смеси [12, с. 274-282].
Способ расчёта плотности упаковки зернистой смеси ![]() , образующейся добавлением к первой самой крупной фракции наполнителя ряда фракций последовательно меньшего размера, чаще всего [13, с. 97-100; 14] сводится к нахождению доли объема пустоты в имеющейся фракции или смеси, заполняемого добавляемой мелкой фракцией.
, образующейся добавлением к первой самой крупной фракции наполнителя ряда фракций последовательно меньшего размера, чаще всего [13, с. 97-100; 14] сводится к нахождению доли объема пустоты в имеющейся фракции или смеси, заполняемого добавляемой мелкой фракцией.
Так, например, в формуле А. Н. Хархардина [14, с. 52]:
![]() , (5)
, (5)
![]() – плотность упаковки уже имеющейся смеси или фракции;
– плотность упаковки уже имеющейся смеси или фракции;
![]() – оставшаяся доля пустоты в упаковке;
– оставшаяся доля пустоты в упаковке;
![]() – коэффициент, характеризующий степень заполнения пустот частицами вводимой фракции. Здесь
– коэффициент, характеризующий степень заполнения пустот частицами вводимой фракции. Здесь ![]() – коэффициент разъединения зёрен смеси, состоящей из n-1 фракций зёрнами вводимой очередной фракции n:
– коэффициент разъединения зёрен смеси, состоящей из n-1 фракций зёрнами вводимой очередной фракции n: ![]() .
.
Для расчета добавляемого количества каждой очередной более мелкой фракции ![]() с плотностью упаковки
с плотностью упаковки ![]() , соответственно, автор применяет формулу:
, соответственно, автор применяет формулу:
| (6) |
![]() , рассчитывается как доля незанятого объема смеси от суммы ранее введенных фракций наполнителей
, рассчитывается как доля незанятого объема смеси от суммы ранее введенных фракций наполнителей ![]() . Так, например, если имеется 1000 г наполнителя с плотностью упаковки 0,6, то в самом простом случае, когда
. Так, например, если имеется 1000 г наполнителя с плотностью упаковки 0,6, то в самом простом случае, когда ![]() , для наибольшего уплотнения упаковки необходимо добавить 400 г зернистого вещества, более мелкой степени измельчения, вне зависимости от его плотности и диаметра частиц.
, для наибольшего уплотнения упаковки необходимо добавить 400 г зернистого вещества, более мелкой степени измельчения, вне зависимости от его плотности и диаметра частиц.
Анализ формул (10) и (11) показывает ее применимость фактически только для расчета упаковок неизменного объема, однако, косвенно рост объёма упаковок признаётся: «Наряду с достигаемым эффектом компактной упаковки частиц, происходит и раздвижка их с увеличением высоты полидисперсного слоя по сравнению с высотой слоя наиболее крупной фракции.» [15, с. 116]. Различия между экспериментальными и теоретическими значениями плотностей упаковок бинарных смесей наполнителей разных диаметров, возникающими в результате эффектов раздвижки и разрыхления, описаны также в работе [16, с. 17-25].
Несколько другой подход можно наблюдать при проектировании составов дисперсно-наполненных полимерных композиционных материалов (ДНПКМ) [17, с. 768-774; 18, с. 4-7; 19, с. 29-36]. Здесь могут иметься структуры с разной степенью наполнения от разбавленных до сверхвысоконаполненных со своими значениями плотности упаковки или максимальной доли наполнителя в материале ![]() . Максимальная доля наполнителя, которую можно ввести в материал, определяется размерами частиц этого наполнителя. Размер частиц может находиться в пределах от нанометров до 50 мкм и более. С уменьшением размера частиц происходит снижение максимальной доли наполнителя в ДНПКМ.
. Максимальная доля наполнителя, которую можно ввести в материал, определяется размерами частиц этого наполнителя. Размер частиц может находиться в пределах от нанометров до 50 мкм и более. С уменьшением размера частиц происходит снижение максимальной доли наполнителя в ДНПКМ.
Плотность упаковки определяет объёмную концентрацию наполнителя в матрице ДНПКМ. Степень наполнения связана с параметром, определяющим долю полимерной матрицы (связующего) для организации непрерывной прослойки между дисперсными частицами наполнителя, причём: ![]() .
.
![]() , (7)
, (7)
![]() – доля полимерного связующего
– доля полимерного связующего
![]() – свободная полимерная часть в ДНПКМ;
– свободная полимерная часть в ДНПКМ;
B – недоступная полимерная часть между частицами;
M – доля полимера в граничном слое.
Аналогично дисперсно наполненным ПКМ, в производстве и разработке лакокрасочных материалов важным показателем является объёмная концентрация пигментов и наполнителей ОКП. ОКП определяет прочностные свойства и адгезию покрытия. В покрытии при небольших ОКП связующее может находиться в свободном состоянии или быть адсорбировано наполнителем. При росте наполнения материала ОКП может достичь критического значения, при котором весь имеющийся объём связующего заполняет пространство между частицами пигментов и наполнителей, расположенными вплотную друг к другу. В этих условиях резко меняются многие свойства лакокрасочного покрытия [20, 21]. Как было показано нами в [22, с. 30-37], критическая концентрация пигментов и наполнителей КОКП и является, практически, плотностью упаковки лакокрасочного материала и может быть рассчитана по простой формуле.
![]() , (8)
, (8)
Здесь: ![]() – плотность упаковки,
– плотность упаковки, ![]() – объём связующего, адсорбированного наполнителем.
– объём связующего, адсорбированного наполнителем.
Таким образом, зная значение плотности упаковки смеси пигментов и наполнителей, в составе лакокрасочного материала, можно оценить максимально возможный уровень его наполнения без ущерба для эксплуатационных свойств.
Состояние наибольшего уплотнения смеси можно получить, например, смочив зёрна наполнителей водой в условиях производства водно-дисперсионных красок при быстром перемешивании фрезой диссольвера [5, с. 42-50]. Тогда частицы компонентов максимально сблизятся, сообразно своей форме и, в отсутствие воздушных прослоек, образуют наиболее плотную упаковку. «Пониженная вязкость и высокое поверхностное натяжение жидкой среды в капиллярах между частицами способствует повышению плотности их упаковки. Олигомерные и полимерные жидкости полностью блокируют поверхностные силы отталкивания частиц в результате образования тонкого межфазного слоя на частицах. Утряска частиц вместе с межфазным слоем на их поверхности приводит к предельной плотности их упаковки» [15, с. 417-418]. Другим способом получения плотной упаковки смеси, относительно её насыпной плотности в свободном состоянии, является сухое виброуплотнение [16, с. 17-25]. Плотность упаковки в этих условиях оказывается несколько меньше, из-за остающегося между зернами воздуха.
Итак, предложим решение задачи по оценке возможности уплотнения смеси двух фракций наполнителей. Найдём условия, при которых плотность упаковки этой смеси будет выше плотности упаковки исходной фракции. Для этого воспользуемся методами математического анализа.
Определим возможность существования экстремума функции плотности упаковки, найдя её производную по массе второй фракции наполнителя. Если график производной переходит через «0» при каком-то соотношении компонентов смеси, то при этом соотношении имеется максимум уплотнения упаковки [23, с. 167-182]. Если же производная на всём протяжении интервала добавления мелкой фракции отрицательна – плотность упаковки в этом интервале снижается и уплотнения смеси произойти не может. Соответственно, при положительной производной, плотность упаковки будет возрастать.
Вычислим производную плотности упаковки смеси по массе добавляемой фракции ![]() , воспользовавшись формулой производной частного [23, с. 140]
, воспользовавшись формулой производной частного [23, с. 140] ![]() . Для удобства раскроем скобки в знаменателе выражения (4):
. Для удобства раскроем скобки в знаменателе выражения (4):
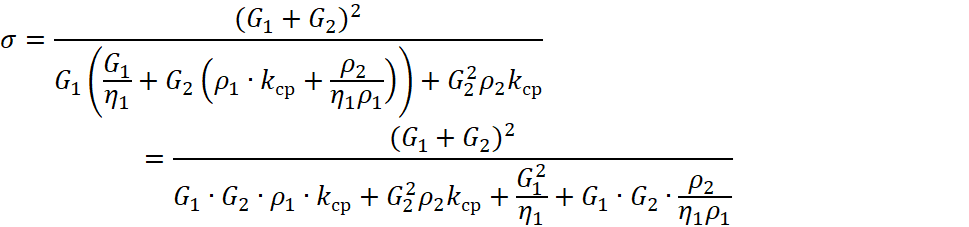 , (9)
, (9)
Далее:
| (10) |
Для дальнейших вычислений удобно преобразовать формулу (10) для ![]() массовой части:
массовой части:
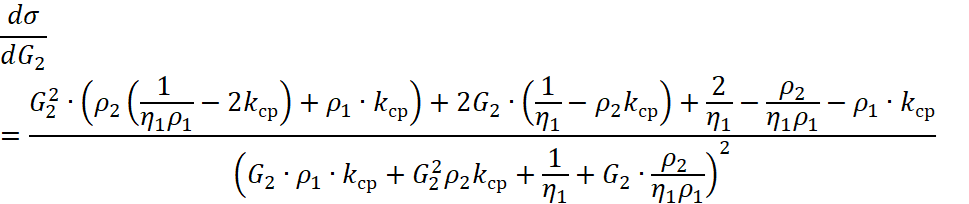 , (11)
, (11)
В случае одинаковых плотностей наполнителей производная плотности упаковки будет равна:
| (12) |
Или на ![]() массовую часть:
массовую часть:
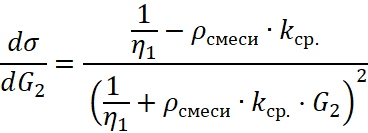 , (13)
, (13)
Теперь рассмотрим две смеси наполнителей: одну смесь двух наполнителей одинаковой плотности, например, микромрамора КМ 0,5–1,0 и КМ 60, а вторую разной плотности, например, микромрамора КМ 10 и нефелинового сиенита [2, 3]. Значения плотностей упаковок этих смесей определены экспериментально в увлажнённом состоянии (табл. 1) [5, с. 42-50]. Экспериментальная зависимость изменения объёма от количества добавленной мелкой фракции для указанных смесей представлена на рисунке 1. С помощью регрессионного анализа в программе Advanced grapher [24] можно определить тангенс угла наклона для каждой смеси: коэффициент ![]() . Таким образом, для КМ 0,5–1,0 + КМ 60
. Таким образом, для КМ 0,5–1,0 + КМ 60 ![]() , а для КМ 10 + нефелиновый сиенит
, а для КМ 10 + нефелиновый сиенит ![]() .
.
Таблица 1
Физические свойства наполнителей
Наполнитель | Плотность, г/см3 | Средний диаметр частиц, мкм | Плотность упаковки увлажнённого наполнителя |
КМ 0,5-1,0 | 2,7 | 640,3 | 0,9266 |
КМ 60 | 2,7 | 24,2 | 0,7935 |
КМ 10 | 2,7 | 10,0 | 0,8319 |
Нефелиновый сиенит | 2,6 | 6,3 | 0,7327 |
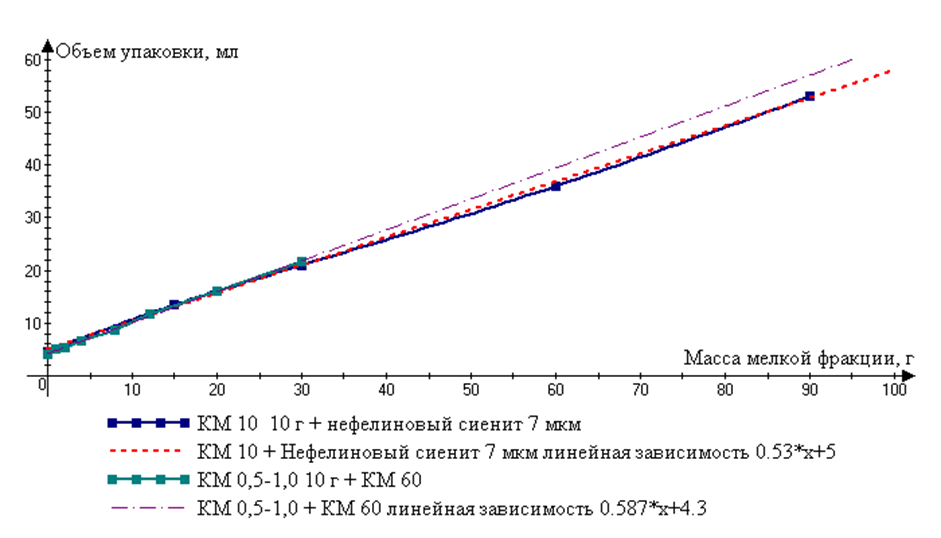
Рис. 1. Зависимость объема увлажненной упаковки от массы мелкой фракции
Значения производной по ![]() для смеси КМ 0,5–1,0 + КМ 60 рассчитываем по формуле (13):
для смеси КМ 0,5–1,0 + КМ 60 рассчитываем по формуле (13):
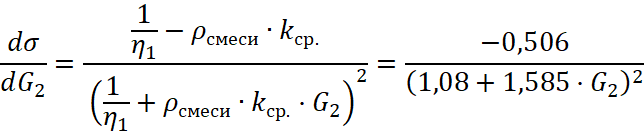 , (14)
, (14)
Для смеси КМ 10 + нефелиновый сиенит, соответственно по формуле (11):
| (15) |
Зависимость производных плотности упаковки двух исследуемых смесей по массе мелкой фракции от массы добавленной мелкой фракции представлена на рисунке 2.
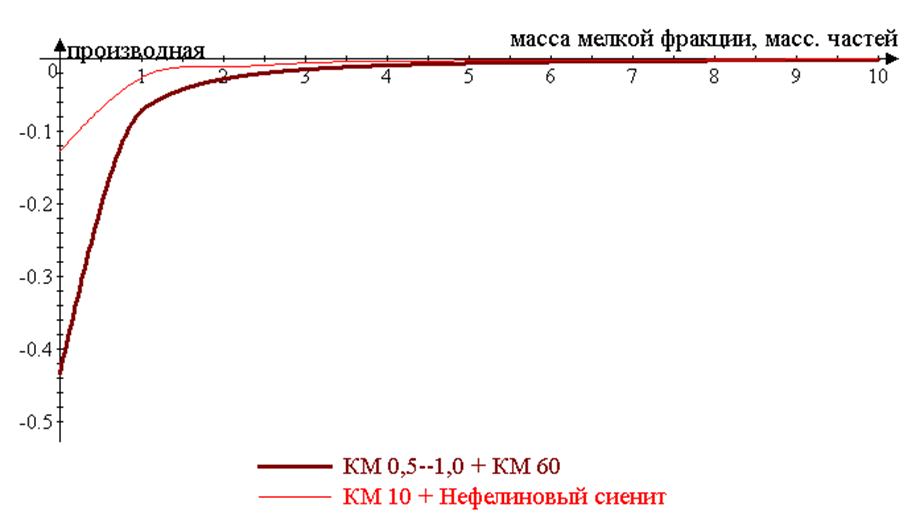
Рис. 2. Производная плотности упаковки по массе мелкой фракции
Характер прохождения графиков производной плотности упаковки для выбранных смесей наполнителей на рисунке 2 указывает на невозможность уплотнения этих смесей при добавлении соответствующих мелких фракций. Оба графика находятся в области отрицательных значений производной, не переходя через ось абсцисс.
Теперь выясним влияние коэффициента ![]() на возможность уплотнения смеси наполнителей. Из формул (2) и (4) следует, что только если коэффициент
на возможность уплотнения смеси наполнителей. Из формул (2) и (4) следует, что только если коэффициент ![]() , роста объёма упаковки при добавлении соответствующих фракций наполнителя не происходит, и всё добавляемое количество наполнителя будет уплотнять смесь, то есть плотность упаковки
, роста объёма упаковки при добавлении соответствующих фракций наполнителя не происходит, и всё добавляемое количество наполнителя будет уплотнять смесь, то есть плотность упаковки ![]() будет возрастать. На практике такая ситуация иногда наблюдается, если количество добавляемой фракции, относительно имеющийся, очень невелико [25, с. 28-34]. Если же
будет возрастать. На практике такая ситуация иногда наблюдается, если количество добавляемой фракции, относительно имеющийся, очень невелико [25, с. 28-34]. Если же ![]() и объём упаковки возрастает, то важно понять, при каких значениях
и объём упаковки возрастает, то важно понять, при каких значениях ![]() будет происходить уплотнение, а при каких разрыхление упаковки.
будет происходить уплотнение, а при каких разрыхление упаковки.
С этой целью, если для какой-либо смеси наполнителей определить значение ![]() , при котором производная функции плотности упаковки по массе мелкой фракции будет равна 0, а сама плотность упаковки постоянна, то, тогда ниже этого значения
, при котором производная функции плотности упаковки по массе мелкой фракции будет равна 0, а сама плотность упаковки постоянна, то, тогда ниже этого значения ![]() упаковка будет уплотняться, а выше его – разрыхлятся.
упаковка будет уплотняться, а выше его – разрыхлятся.
Приравнивая выражение (10) к нулю, получаем:
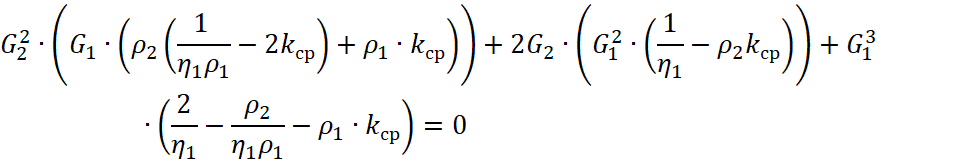 , (16)
, (16)
Отсюда, раскрывая скобки:
| (17) |
На 1 массовую часть ![]() :
:
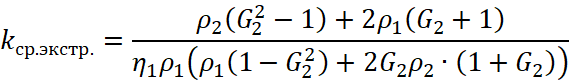 , (18)
, (18)
Если в (9) рассчитать, для ![]() , имеем:
, имеем:
![]() , (19)
, (19)
В случае одинаковых плотностей наполнителей выражение для ![]() упрощается:
упрощается:
| (20) |
Аналогичный результат можно получить из формулы (13).
Таким образом, вычислив значение ![]() по формулам (17), (19) или (20), можно понять, будет ли смесь уплотнятся или разрыхлятся от добавления мелкой фракции, при экспериментально определённом значении
по формулам (17), (19) или (20), можно понять, будет ли смесь уплотнятся или разрыхлятся от добавления мелкой фракции, при экспериментально определённом значении ![]() . Физический смысл формулы (20) состоит в том, что чем более рыхлая упаковка исходной крупной фракции смеси (
. Физический смысл формулы (20) состоит в том, что чем более рыхлая упаковка исходной крупной фракции смеси (![]() меньше), тем сильнее (
меньше), тем сильнее (![]() больше) может расти объём смеси при добавлении мелкой фракции, с сохранением возможности уплотнения упаковки. Из формул (17), (19) и (20) следует также, что
больше) может расти объём смеси при добавлении мелкой фракции, с сохранением возможности уплотнения упаковки. Из формул (17), (19) и (20) следует также, что ![]() фактически зависит только от плотности упаковки исходной фракции
фактически зависит только от плотности упаковки исходной фракции ![]() , и будет одинакова при смешивании с ней любой последующей фракции любого наполнителя.
, и будет одинакова при смешивании с ней любой последующей фракции любого наполнителя.
Так как в условиях эксперимента ранее было взято 50 г микромрамора КМ 0,5–1,0 рассчитаем плотность упаковки смеси КМ 0,5–1,0 + КМ 60 для ![]() массовых частей:
массовых частей:
| (21) |
При ![]() плотность упаковки постоянна и не зависит от количества мелкой фракции. При экспериментальном значении
плотность упаковки постоянна и не зависит от количества мелкой фракции. При экспериментальном значении ![]() производная плотности упаковки отрицательна – плотность упаковки снижается:
производная плотности упаковки отрицательна – плотность упаковки снижается:
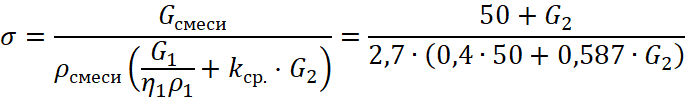 , (22)
, (22)
При гипотетическом ![]() производная плотности упаковки положительна – плотность упаковки повышается и становится даже больше 1, что не имеет физического смысла (рис. 3):
производная плотности упаковки положительна – плотность упаковки повышается и становится даже больше 1, что не имеет физического смысла (рис. 3):
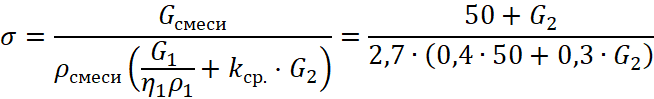 , (23)
, (23)
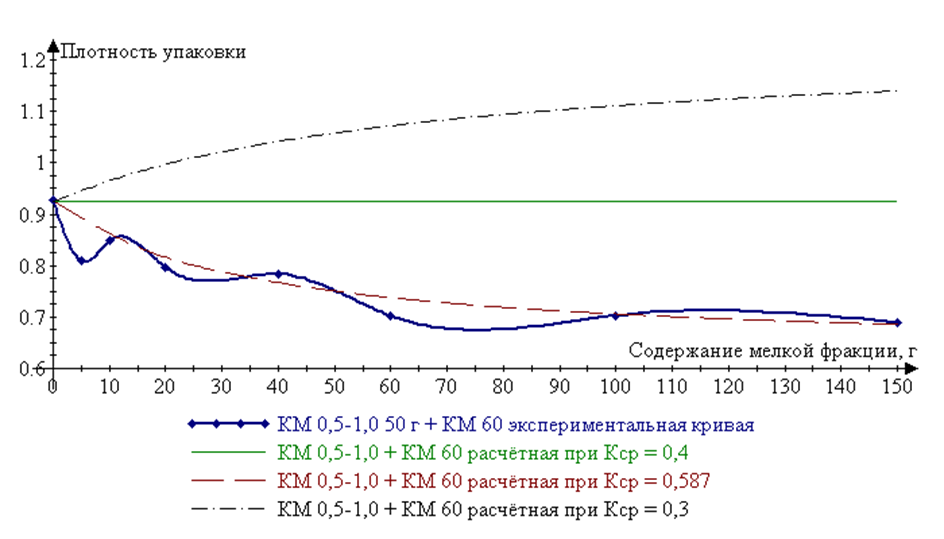
Рис. 3. Зависимость плотности упаковки смеси от содержания мелкой фракции
Аналогично, вычислим ![]() , по формуле (9) для смеси КМ 10 + нефелиновый сиенит, для одной массовой части КМ 10 и одной массовой части нефелинового сиенита (
, по формуле (9) для смеси КМ 10 + нефелиновый сиенит, для одной массовой части КМ 10 и одной массовой части нефелинового сиенита (![]() ):
):
![]() , (24)
, (24)
Подставляя значение ![]() в формулу (4), для
в формулу (4), для ![]() получим:
получим:
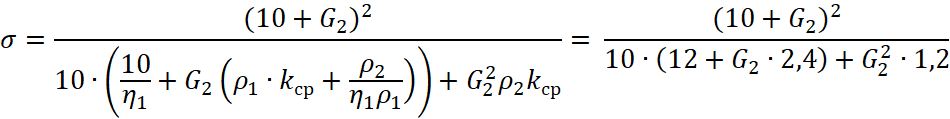 , (25)
, (25)
График изменения плотности упаковки будет представлять собой прямую, параллельную оси абсцисс. Если ![]() , например
, например ![]() , тогда:
, тогда:
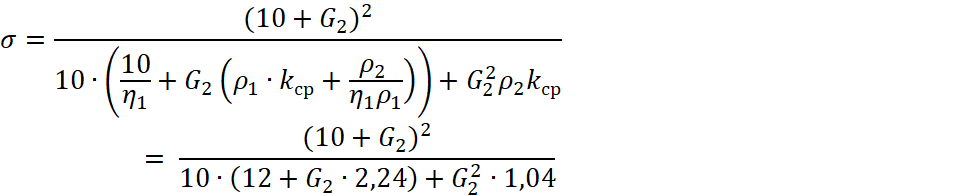 , (26)
, (26)
При этом значении ![]() плотность упаковки будет возрастать. При экспериментально определённом значении
плотность упаковки будет возрастать. При экспериментально определённом значении ![]() , что больше
, что больше ![]() , плотность упаковки исследуемой смеси снижается при увеличении содержания мелкой фракции (рис. 4):
, плотность упаковки исследуемой смеси снижается при увеличении содержания мелкой фракции (рис. 4):
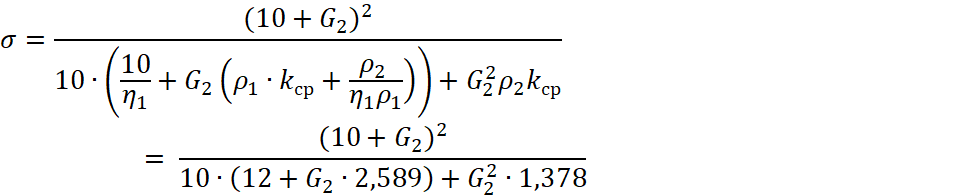 , (27)
, (27)
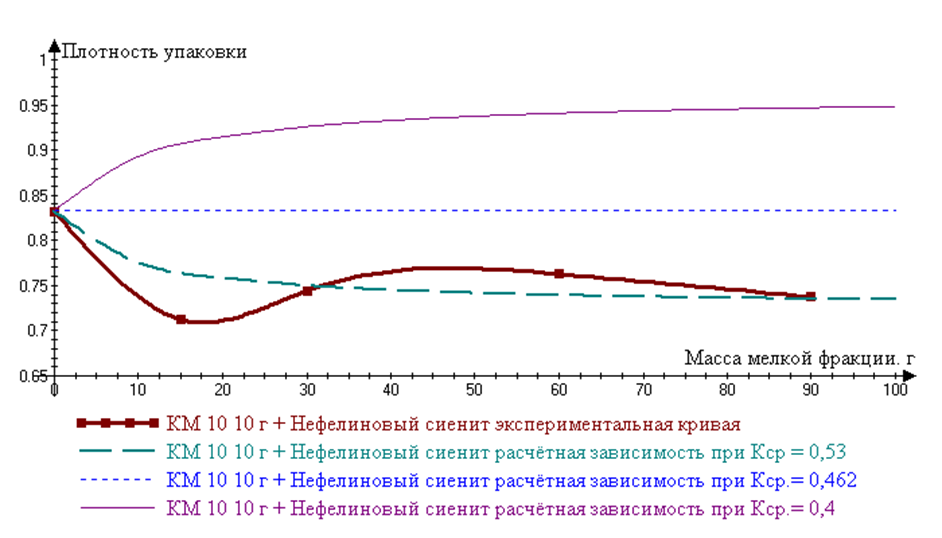
Рис. 4. Зависимость плотности упаковки смеси от содержания мелкой фракции
Приведём пример упаковки наполнителей, в которой экспериментальное значение ![]() оказывается больше, чем
оказывается больше, чем ![]() . Например, сухая уплотнённая упаковка двух фракций микромрамора: КМ 0,5–1,0 и КМ 100 (табл. 2). На самом деле, экспериментально определённое значение
. Например, сухая уплотнённая упаковка двух фракций микромрамора: КМ 0,5–1,0 и КМ 100 (табл. 2). На самом деле, экспериментально определённое значение ![]() [4, с. 26-32], а
[4, с. 26-32], а ![]() .
.
Таблица 2
Физические свойства наполнителей
Наполнитель | Плотность, г/см3 | Средний диаметр частиц, мкм | Плотность упаковки сухого наполнителя |
КМ 0,5-1,0 | 2,7 | 782,3 | 0,5737 |
КМ 100 | 2,7 | 27,5 | 0,6119 |
Для 20 массовых частей ![]() при
при ![]() :
:
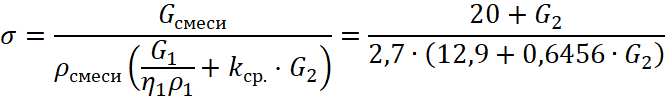 , (28)
, (28)
График плотности упаковки представляет собой прямую, а если ![]() и, соответственно:
и, соответственно:
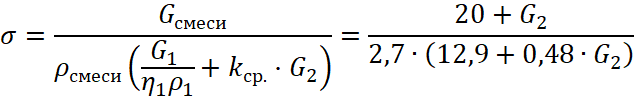 , (29)
, (29)
То расчётная плотность упаковки растёт при добавлении КМ 100, аналогично эксперименту (рис. 5).
Также, при экспериментальном значении ![]() , производная плотности упаковки КМ 0,5–1,0 + КМ 100 положительна на всем интервале добавления мелкой фракции (рис. 6):
, производная плотности упаковки КМ 0,5–1,0 + КМ 100 положительна на всем интервале добавления мелкой фракции (рис. 6):
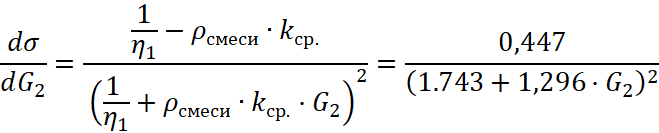 , (30)
, (30)
Из изложенного следует, что при смешении двух фракций наполнителей с разным диаметром зёрен, плотность упаковки получаемой смеси может либо возрастать при любом количестве добавляемой мелкой фракции, либо убывать. Возможность уплотнения той или иной смеси зависит только от величин ![]() . В случае отсутствия экспериментальных значений
. В случае отсутствия экспериментальных значений ![]() для исследуемых смесей, их можно приблизительно рассчитать, используя эмпирические формулы, приведённые в [4, с. 26-32; 5, с. 42-50].
для исследуемых смесей, их можно приблизительно рассчитать, используя эмпирические формулы, приведённые в [4, с. 26-32; 5, с. 42-50].
Таким образом, с помощью математического анализа разработан метод оценки возможности уплотнения смеси минеральных наполнителей при добавлении более мелкой фракции наполнителя к более крупной, основанный на влиянии величины роста объёма упаковки этой смеси.
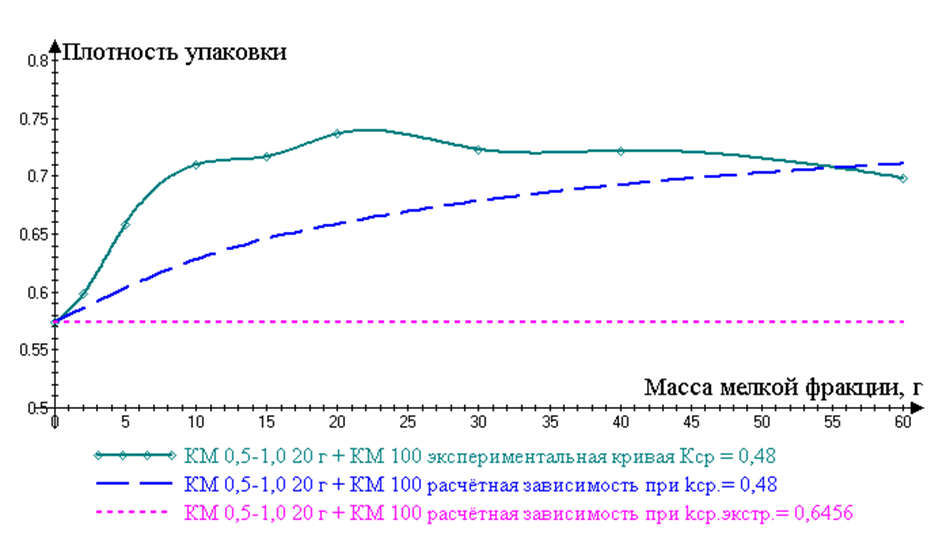
Рис. 5. Зависимость плотности упаковки смеси от содержания мелкой фракции
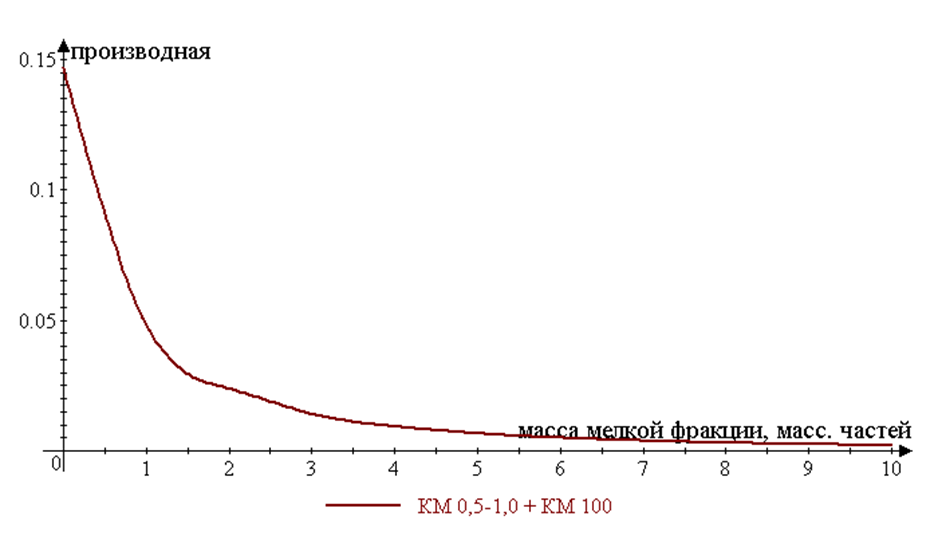
Рис. 6. Производная плотности упаковки по массе мелкой фракции
.png&w=384&q=75)
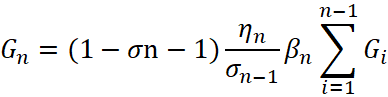
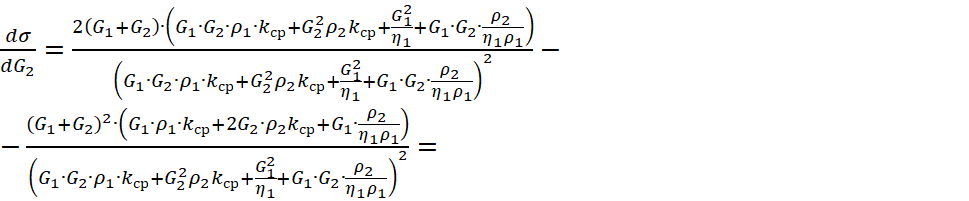
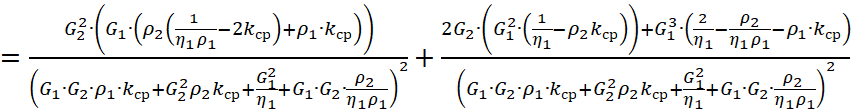 ,
,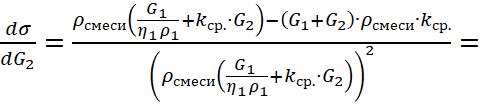
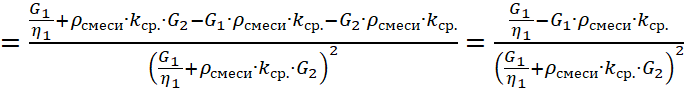 ,
,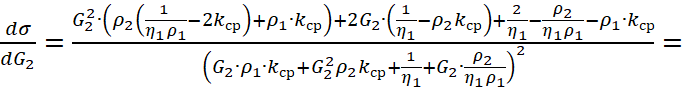
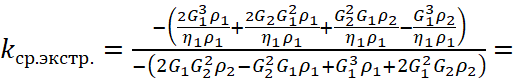
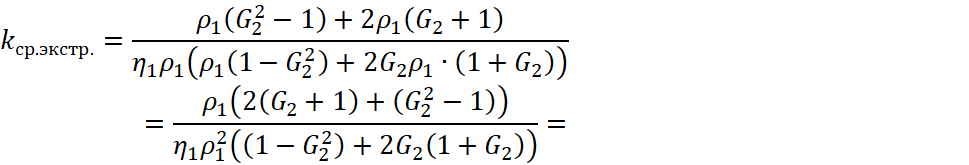
.png&w=640&q=75)