Использование имитационно-стохастической модели расчета параметров процесса эвакуации из помещений многофункциональных эллингов

Здания многофункциональных эллингов – это комплексы зданий и сооружений у воды, которые предназначены для хранения и обслуживания водного транспорта (лодок, катеров, яхт), а также могут включать жилые помещения (коттеджи, гостиницы) и дополнительную инфраструктуру. Они служат как для защиты судов от непогоды, так и для отдыха или постоянного проживания, сочетая в себе функции гаража, дома и сервисного центра. В случае возникновения пожара в подобном здании необходима эвакуация людей, т. е. выполнение мероприятий, направленных на их своевременное и безопасное удаление из здания.

Для прогнозирования и анализа движения людей в чрезвычайных ситуациях, таких как пожары, землетрясения и др., часто используется моделирование с использованием математических моделей и компьютерных программ. Цель моделирования – оценить необходимое время для эвакуации, выявить «узкие места» и предложить пути оптимизации путей и планов эвакуации.

Ценным ресурсом для документирования процесса эвакуации из зданий многофункциональных эллингов может служить запись видеоматериалов.

В эксперименте участвовало 14 человек. Полученные в результате видеообработки значения скоростей движения людей при определенной плотности были распределены в виде выборок по сериям натурных наблюдений в зависимости от вида пути, после чего был проведен первичный статистический анализ данных.

Для определения достоверности полученных эмпирических данных с заданной доверительной вероятностью P = 0,95 в работе была проведена проверка необходимой численности измерений (n) по формуле (1):

, (1)

Где x – коэффициент доверительной вероятности P(x), для P(0,95) = 1,96; – значение меры изменчивости , представляющее собой выраженное в % отношение среднеквадратического отклонения () выборки к среднему арифметическому значению (); – показатель точности исследования, равный допустимой ошибке, не превышающей 3–5%.

Убедившись в достаточной численности измерений, проводили дальнейшую статистическую обработку, а именно проверку гипотезы об однородности эмпирических выборок с применением широко известных статистических критериев [1, с. 10-16]. Алгоритм проверки полученных выборок на однородность проводился согласно рекомендациям, приведенным в [2, 3], для малых выборок, численностью от 3 до 50 значений, был применен критерий Шапиро-Уилка [4, с. 591-611].

Проверка на нормальность показала, что распределение каждой выборки описывается нормальным законом распределения. Проверка на наличие грубых погрешностей при помощи правила трех сигм () показала, что все значения в выборках лежат в интервалах (; ).

После того как выяснилось, что все значения в выборках подчиняются нормальному закону распределения, была проведена проверка выборок из разных серий наблюдений на однородность при помощи параметрического критерия – t-критерия Стьюдента, проверяющего равенство средних значений. Чтобы исключить возможность его ошибочного применения, нужно учитывать наличие или отсутствие однородности дисперсий в исследуемых выборках. С этой целью применялся F-критерий Фишера [5, с. 308-31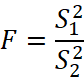2]:

, (2)

Где – дисперсия большей выборки, а – дисперсия меньшей выборки.

Полученные результаты сравнивались с критическими значениями F-критерия Фишера на уровне значимости α = 0,05, для определения возможности однородности дисперсий с учетом числа степеней свободы.

Для установления расчётных зависимостей между скоростью движения и плотностью потока людей в здания многофункционального эллинга использовалась апробированная методология, используемая специалистами научной школы «Теория людских потоков при эвакуации» [6]. Скорость людского потока V при его плотности D описывается как средняя скорость движения людей V_D и в общем виде выражается как:

, (3)

Где V₀ – случайная величина скорости свободного движения людского потока по участку пути, когда значение плотности не оказывает на нее влияние, м/мин; функция R, входящая в данное уравнение, отображает степень (силу) влияния внешнего фактора на сенсорную систему человека, формирующую интенсивность реакции (в данном случае скорости движения) человека. Функция R не зависит от уровня эмоционального состояния людей, и отражает тенденцию влияния плотности людского потока D на скорость их движения.

Для определения вида этой зависимости при движении людей, необходимо установить параметры входящей в ее состав относительной величины R= f(D). С этой целью, по результатам экспериментальных данных строятся эмпирические функции R_D= f(D) для каждого интервала плотности.

Эмпирические значения R_D для каждого интервала плотности во всех сериях проведенных натурных наблюдений определяются по формуле:

, (4)

Где , m(V₀) – математическое ожидание скорости свободного движения в интервале плотности 0–1 чел/м²;

m(V_D) – математическое ожидание скорости в интервале плотности, для которого определяется степень влияния внешнего фактора на сенсорную систему человека.

Далее проводилась аппроксимация полученных данных. В основе проявляющегося влияния плотности людского потока на его скорость лежат психофизические закономерности взаимосвязи между физическими характеристиками различного характера стимулов, порождаемых плотностью людского потока, и интенсивностью ощущений, реакцией на которые и является изменение скорости движения людей. Это описывается теоретической зависимостью, соответствующей логарифмическим соотношениям Вебера-Фехнера [7, с. 284-288]:

, (5)

Где D – значение плотности людского потока, при котором определяется значение ;

D₀ – пороговое значение плотности, по достижении которого она начинает ощущаться как воздействующий фактор при движении по участку пути;

a – эмпирический коэффициент, отображающий интенсивность воздействия плотности при движении людей. Коэффициенты a и D₀ в приведенном выше выражении были определены методом средних и методом наименьших квадратов.

О корректности проведенной аппроксимации свидетельствует нахождение теоретической кривой в 95%-м доверительном интервале от средних значений.

В качестве показателя тесноты связи между признаком – фактором, в качестве которого выступает плотность людского потока, и признаком – результатом (величина R) использовалось корреляционное отношение, определяемое по выражению 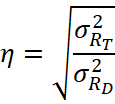(6):

, (6)

Где – дисперсия теоретических значений величины R_Т, а – дисперсия эмпирических значений величины R_D.

Полученные результаты подтверждают теорию Холщевникова [6] о психофизическом влиянии воздействия внешних факторов на скорость движения людей по различным видам пути. Эмоциональное состояние и стресс, вызванные внешними условиями, могут существенно повлиять на скорость и эффективность передвижения. Увеличение плотности людей в потоке приводит к снижению скорости.

Математическое описание основной функциональной связи V= ƒ(D) при движении людей по эвакуационным путям и через эвакуационные выходы описывается формулой (7):

, (7)

Где: V₀ – скорость свободного движения людей, м/мин; a – коэффициент, определяющий степень влияния плотности людского потока на его скорость; D – текущее значение плотности людского потока, чел/м²; D₀ – пороговое значение плотности людского потока, по достижении которого плотность становится фактором, влияющим на скорость движения, чел/м².

Полученные в результате аппроксимации эмпирических данных коэффициенты a, D₀ и V₀ для уравнения (7) определяют основные параметры движения людей по различным маршрутам, что позволяет проводить расчеты для определения времени, затраченного на процесс движения. Значения вышеуказанных коэффициентов приведены в таблице.

Таблица

Значения коэффициентов a, D₀ и V₀, характеризующих движение людей по путям эвакуации и через эвакуационные выходы

Знание таких зависимостей позволяет оптимизировать внутреннее устройство здания многофункционального эллинга, где движение людей является важным. Понимание динамики людских потоков может помочь в разработке более эффективных стратегий эвакуации в экстренных ситуациях.

Таким образом, в настоящей работе проведен статистический анализ движения людей при эвакуации по горизонтальным участкам, лестнице вниз и через проемы, учитывая, что скорость и поведение людей зависят от множества факторов, таких как физическое состояние, опыт и уровень стресса. Выполнена аппроксимация функции R в зависимости от плотности людского потока D. Полученные модели, основанные на логарифмической зависимости по закону Вебера–Фехнера, позволяют более точно описывать связь между плотностью потока и скоростью передвижения. На основе этих данных предложены коэффициенты в имитационно-стохастической модели для расчета процесса эвакуации в помещениях многофункциональных эллингов.