Задача Коши является одной из основных задач в теории дифференциальных уравнений, характеризующей начальные условия для решения. Эта задача имеет множество приложений в физике, инженерии и других областях науки. Одним из наиболее мощных инструментов для решения задач Коши является преобразование Фурье, которое позволяет преобразовывать дифференциальные уравнения в алгебраические, что значительно упрощает их анализ и решение.
Формулировка задачи Коши
В общем виде задача Коши для уравнения в частных производных может быть представлена как:
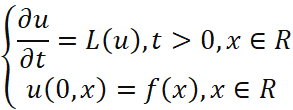 , (1)
, (1)
Где L – линейный дифференциальный оператор f(x) – заданная функция, представляющая начальные условия, а u(t, x) – искомая функция.
Преобразование Фурье
Преобразование Фурье функции u(t, x) – определяется как:
| (2) |
Применение преобразования Фурье к уравнению Коши позволяет преобразовать его в более удобную форму. Например, L если является линейным оператором, то можно записать:
![]() , (3)
, (3)
Где ![]() преобразование оператора L в частотной области.
преобразование оператора L в частотной области.
Решение задачи Коши с помощью преобразования Фурье
- Применение преобразования: применяем преобразование Фурье к начальным условиям и уравнению. Это преобразует задачу Коши в задачу о решении обыкновенного дифференциального уравнения (ОДУ) для
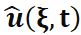 .
. - Решение ОДУ: полученное ОДУ можно решить с использованием стандартных методов. Решение будет иметь вид:
![]() , (4)
, (4)
Где ![]() – преобразование Фурье начальных условий.
– преобразование Фурье начальных условий.
- Обратное преобразование: после нахождения
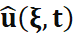 необходимо выполнить обратное преобразование Фурье, чтобы вернуться к пространственной области:
необходимо выполнить обратное преобразование Фурье, чтобы вернуться к пространственной области:
| (5) |
Пример: уравнение теплопроводности
Рассмотрим уравнение теплопроводности:
![]() , (6)
, (6)
Где k – коэффициент теплопроводности.
- Применяя преобразование Фурье, получаем:
![]() , (7)
, (7)
- Решение ОДУ:
![]() , (8)
, (8)
- Для начальных условий
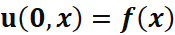 , имеем:
, имеем:
| (9) |
Это представление дает решение задачи Коши через интеграл, который можно интерпретировать как пространственный разворот функции с фактором, описывающим «распространение» тепла во времени.
Заключение
Точные решения задачи Коши с использованием преобразования Фурье являются мощным методом в теории дифференциальных уравнений. Это преобразование позволяет не только находить аналитические решения, но и применять численные методы для изучения более сложных уравнений. Применение преобразования Фурье эффективно упрощает задачу анализа динамических систем, создавая мощные инструменты для решения многообразных задач в прикладных науках.
.png&w=384&q=75)
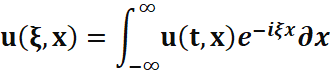
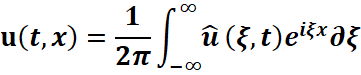
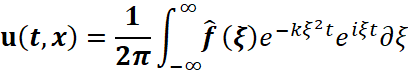
.png&w=640&q=75)