Современная эпоха глобальной цифровой трансформации характеризуется повсеместным внедрением технологий компьютерного инжиниринга (Computer-Aided Engineering) в процессы проектирования и исследования новых материалов и устройств. Численное моделирование, в основе которого лежит решение систем дифференциальных уравнений методами конечных элементов (МКЭ) или конечных разностей (МКР), стало неотъемлемым инструментом ученого и инженера.
Однако, возрастающая сложность расчетных моделей и программного обеспечения ставит острую проблему верификации - подтверждения того, что численная алгоритмическая модель правильно представляет исходную математическую модель.
Распространенные подходы к верификации, такие как сравнение с экспериментальными данными, часто являются дорогостоящими и не всегда осуществимыми на ранних стадиях проектирования. Перекрестная проверка различными программными пакетами также не гарантирует достоверности, так как разные решатели могут быть основаны на сходных численных схемах и, следовательно, содержать схожие погрешности.
В этом контексте точные аналитические решения дифференциальных уравнений приобретают новую, прикладную роль – роль независимого и абсолютного эталона для тестирования вычислительных алгоритмов. Они позволяют количественно оценить погрешность численного метода, исследовать его сходимость и выявить слабые места.
Цель данной работы – продемонстрировать методику верификации коммерческого CAE-пакета на примере классической задачи теплообмена в двухслойной среде, используя в качестве эталона точное аналитическое решение, полученное методом разделения переменных.
1. Постановка аналитической задачи
Рассматривается задача о стационарной теплопроводности в двухслойной прямоугольной пластине (рис. 1). Пластина состоит из двух разнородных изотропных материалов с коэффициентами теплопроводности ![]() и
и ![]() . На левой границе x=0 поддерживается постоянная температура
. На левой границе x=0 поддерживается постоянная температура ![]() на правой границе x = L – температура
на правой границе x = L – температура ![]() . Боковые поверхности теплоизолированы.
. Боковые поверхности теплоизолированы.
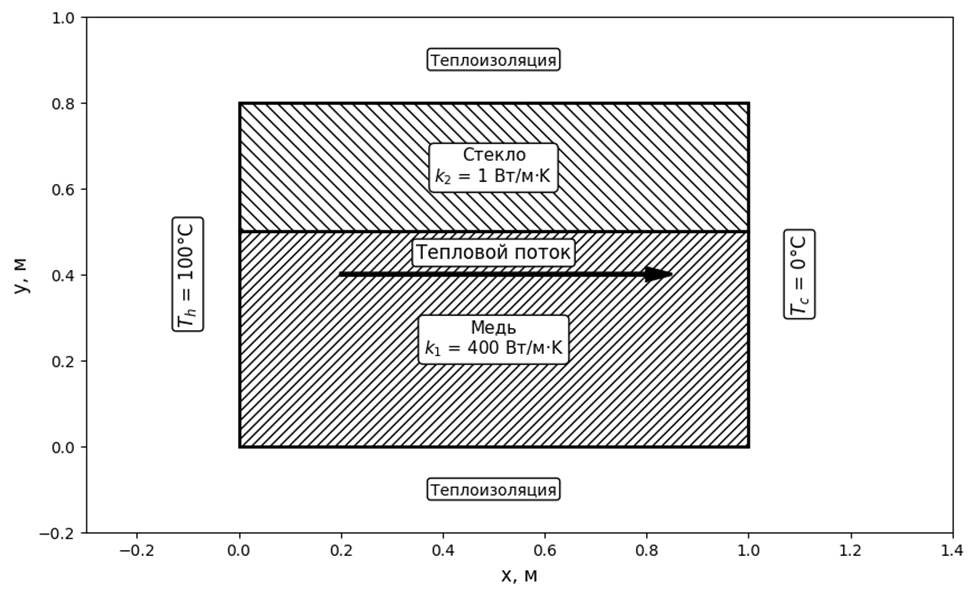
Рис. 1. Расчетная схема двухслойной пластины
Математическая модель описывается уравнением Лапласа для каждой области:
![]() , (1)
, (1)
![]() , (2)
, (2)
Граничные условия и условия сопряжения на границе раздела сред (![]() ) формулируются как:
) формулируются как:
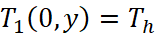 ,
,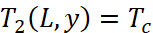 ,
,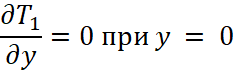 ,
,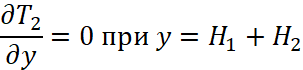 ,
,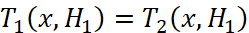 (неразрывность температуры),
(неразрывность температуры),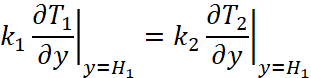 (неразрывность теплового потока).
(неразрывность теплового потока).
2. Метод решения
Для решения задачи применяется метод разделения переменных Фурье. Решение ищется в виде суммы произведений функций, зависящих только от x и только от y. Учитывая однородность граничных условий по y, решение строится в виде ряда [2]:
| (3) |
Где i = 1, 2 – номер слоя, ![]() – собственные значения, определяемые из граничных условий,
– собственные значения, определяемые из граничных условий, ![]() – постоянные интегрирования, определяемые из условий сопряжения и неоднородных граничных условий по x.
– постоянные интегрирования, определяемые из условий сопряжения и неоднородных граничных условий по x.
3. Результаты и обсуждение
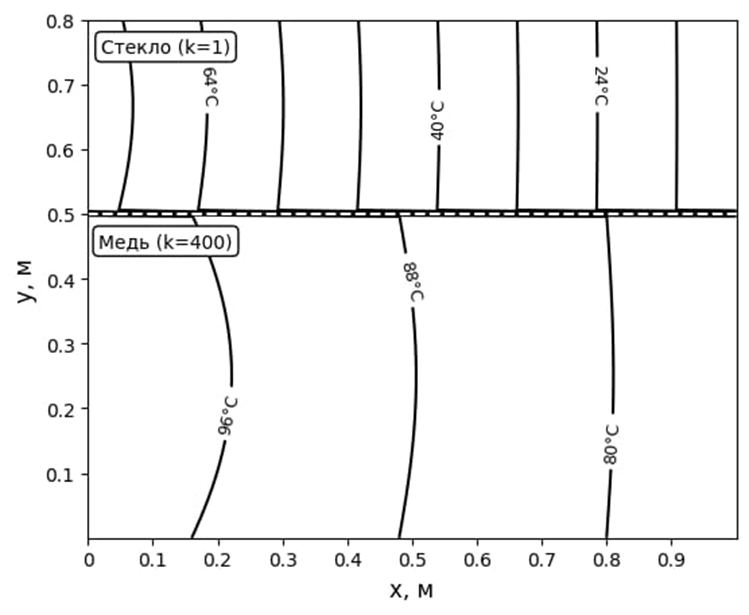
Рис. 2. Распределение температуры в двухслойной пластине (аналитическое решение)
Анализ решения показывает:
- Излом изотерм на границе раздела сред – характерный признак различных теплопроводностей;
- Разная плотность изотерм: в меди (k₁=400 Вт/м·K) – редкие, в стекле (k₂=1 Вт/м·K) – частые.
4. Критерии для верификации численных методов
Предлагаются количественные метрики для проверки вычислительных алгоритмов:
- Контрольные точки с эталонными значениями температуры;
- Углы излома изотерм на границе раздела сред;
- Нормы невязки уравнений теплопроводности.
Таблица
Эталонные значения температуры
Контрольная точка | Температура, °C |
(0.2, 0.2) | 96.0 |
(0.5, 0.4) | 88.0 |
(0.8, 0.7) | 24.1 |
(0.8, 0.15) | 80.0 |
Методика применения тестового примера:
- Реализовать расчет данной задачи в проверяемом программном комплексе;
- Сравнить результаты с эталонными значениями из таблицы;
- Оценить погрешность по предложенным метрикам;
- Проанализировать сходимость при измельчении сетки.
В ходе работы была успешно продемонстрирована методика верификации программного обеспечения для численного моделирования с использованием точного аналитического решения.
На примере задачи теплопроводности в двухслойной пластине показано, что даже для относительно простой геометрии, наличие границы раздела сред создает область повышенной численной погрешности.
Точные аналитические решения являются мощным и строгим инструментом для верификации вычислительных алгоритмов и коммерческих CAE-пакетов.
Разработанный эталонный пример для двухслойной структуры может быть использован для тестирования решателей задач теплопроводности и механики.
Предложенный подход повышает надежность результатов цифрового проектирования, что является критически важным при создании ответственных конструкций и устройств. Методика может быть расширена на другие классы физических задач.
Внедрение методологии, основанной на использовании аналитических эталонов, позволит:
- Снизить риски при проектировании за счет повышения достоверности моделей.
- Создать библиотеку тестовых примеров для валидации как коммерческого, так и самописного программного обеспечения.
- Заложить основу для разработки стандартов верификации расчетных моделей в инженерной практике, что соответствует духу эпохи цифровой трансформации, требующей не только скорости, но и подтвержденного качества вычислений.
.png&w=384&q=75)
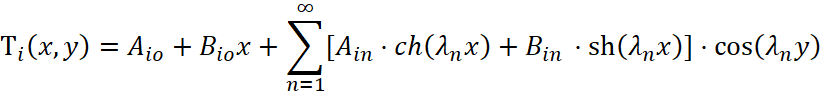
.png&w=640&q=75)