Фундаментальные решения дифференциальных операторов как инструмент верификации вычислительных моделей в физике

Современное цифровое проектирование в физике и инженерии немыслимо без применения численного моделирования. Возникает ключевая проблема обеспечения достоверности результатов, получаемых с помощью PDE-солверов (Partial Differential Equation solvers). Одним из наиболее надежных методов верификации является сравнение численного решения с точным аналитическим. В данной связи концепция фундаментального решения (ФР) дифференциального оператора представляется чрезвычайно плодотворной. Данный математический объект, являясь откликом системы на точечное воздействие, не только имеет глубокую физическую интерпретацию, но и позволяет конструктивно строить решения для широкого класса задач.

Цель настоящей работы – показать единство математической природы и физического смысла фундаментальных решений и обосновать их применение в качестве эталонов для тестирования вычислительных алгоритмов.

Основу methodology составляет аппарат теории обобщенных функций и интегральных преобразований. Фундаментальное решение линейного дифференциального оператора с постоянными коэффициентами P (D) определяется как обобщенная функция Ε, удовлетворяющая уравнению , где – дельта-функция Дирака. Ключевым методом нахождения ФР является преобразование Фурье, позволяющее свести дифференциальное уравнение к алгебраическому. Для визуализации и интерпретации результатов применяются методы качественного анализа и построения графических моделей полей, порождаемых точечными источниками.

Понятие фундаментального решения

Фундаментальное решение – один из ключевых объектов в теории линейных дифференциальных уравнений с постоянными коэффициентами.

Фундаментальным решением дифференциального оператора P(D) называется обобщённая функция E(x), удовлетворяющая уравнению:

, (1)

Где – дельта-функция Дирака.

Физический смысл фундаментального решения становится ясен при рассмотрении неоднородного уравнения:

, (2)

Формальное решение этого уравнения можно записать в виде свертки:

, (3)

Эта формула имеет прозрачную физическую интерпретацию: результирующее поле u(x) представляет собой суперпозицию (сумму) полей E(x - y), создаваемых элементарными источниками f(y)dy.

Рассмотрим фундаментальные решения основных операторов математической физики.

1. Оператор Лапласа. Для оператора Лапласа в трёхмерном пространстве уравнение для фундаментального решения имеет вид:

, (4)

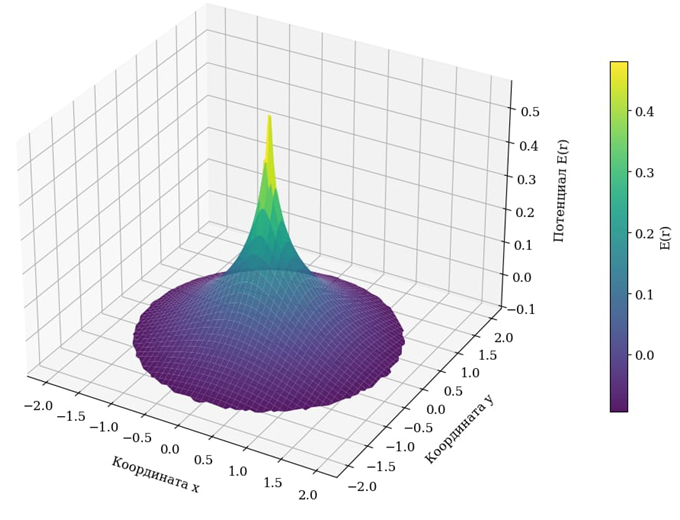
Рис. 1. Фундаментальное решение оператора Лапласа (потенциал точечного источника)

Применяя преобразование Фурье к обеим частям уравнения, получаем:

, откуда .

Выполняя обратное преобразование Фурье, находим:

, (5)

Физическая интерпретация: это классический потенциал точечного заряда в электростатике или точечной массы в гравитации.

2. Оператор теплопроводности. Для оператора теплопроводности уравнение имеет вид:

, (6)

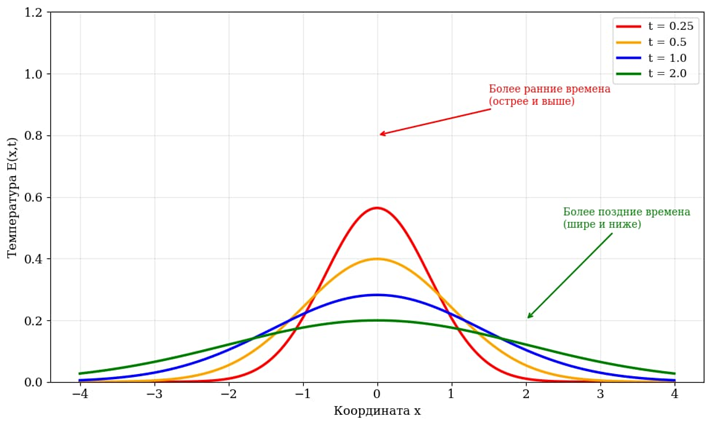
Рис. 2. Фундаментальное решение уравнения теплопроводности: распределение температуры от мгновенного точечного источника в различные моменты времени

Применяя преобразование Фурье по пространственным переменным, получаем:

, (7)

Решение этого уравнения с учётом условия причинности (E = 0 при t < 0) даёт:

, (8)

Где θ(t) – функция Хевисайда.

Обратное преобразование Фурье приводит к ядру Пуассона:

, (9)

Физическая интерпретация: распределение температуры от мгновенного точечного источника тепла.

3. Волновой оператор. Для волнового оператора в трёхмерном пространстве:

, (10)

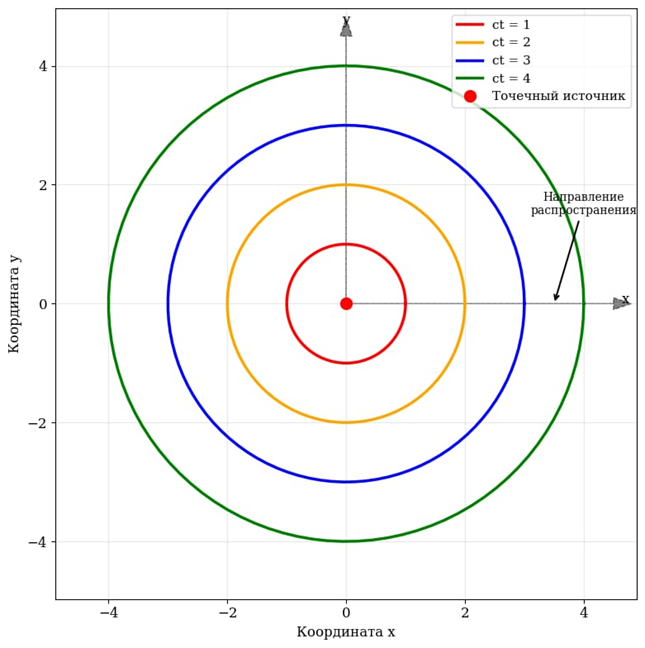
Рис. 3. Фундаментальное решение волнового уравнения: расходящийся сферически волновой фронт от точечного импульсного источника в различные моменты времени

Фундаментальное решение имеет вид:

, (11)

Физическая интерпретация: сферическая волна, расходящаяся от точечного импульсного источника.

Верификация вычислительных алгоритмов. Фундаментальные решения предоставляют идеальные тестовые случаи для верификации PDE-солверов. Процедура верификации включает:

1. Решение численной задачи с точечным источником, моделируемым δ-функцией.
2. Сравнение результата с аналитическим фундаментальным решением.
3. Оценку погрешности в различных нормах.

Такой подход позволяет выявить систематические погрешности дискретизации и проверить корректность реализации граничных условий.

Проведенный анализ подтверждает, что фундаментальные решения являются не абстрактными конструктами, а адекватными математическими моделями базовых физических полей. Их вычисление и анализ составляют ядро классической теории дифференциальных уравнений в частных производных.

Выводы и ожидаемый эффект:

1. Фундаментальное решение представляет собой аналитический эталон – точное решение задачи с точечным источником.
2. Сравнение численных результатов, полученных для модели с точечным источником, с соответствующим фундаментальным решением является одним из наиболее строгих тестов корректности и точности вычислительного алгоритма.
3. Использование ФР для верификации позволяет выявить системные погрешности методов, связанные с дискретизацией, аппроксимацией и решением систем уравнений.
4. Ожидаемый эффект от внедрения данной методологии верификации – повышение надежности и доверия к результатам цифрового проектирования в таких областях, как микроэлектроника (моделирование перегрева), акустика и механика деформируемого твердого тела.