1. Физическая интерпретация общей формулы Мироздания по соответствию известному инвариантному энергетическому соотношению и пространственно-временным преобразованиям по СТО и ОТО Эйнштейна
В статье [1, с. 6-42] на основе элементарной логики были определены основные закономерности построения Мироздания и выведена общая формула Мироздания связи глобальных противоположностей в виде:
| (1) |
Здесь w=(-1)1/2x. Иными словами отличие объектов от противоположностей определяется атрибутом принадлежности в виде i=(-1)1/2, что и определяет смену закономерностей в зависимости от системы наблюдения при сохранении количественного равенства.
Понятно, что из общей формулы Мироздания должны следовать и известные законы физики с учётом констант, полученные в экспериментах, так как иное означало бы разрыв с наличием чудес. Из (1) видно, что левую часть уравнения до знака равенства можно рассматривать представлением взаимодействия в одной глобальной противоположности в виде нормированного уравнения окружности, а правая часть формулы соответствует инвариантной форме используемой в СТО в виде: s2=c2T2-R2 , что и было показано в [1, с. 6-42]. При этом общая формула Мироздания отражает процессы в противоположностях с учётом того, что сложение в одной противоположности означает вычитание в другой противоположности. Иное бы означало отсутствие отличий между противоположностями. Для показа связи общей формулы мироздания (1) с известными физическими законами представим левую часть общей формулы Мироздания с учётом взаимодействия противоположностей через переменные с нормировкой к скорости обмена равной скорости света. Собственно, при условии сохранения объекта, динамика взаимодействия противоположных частей объекта, с учётом наблюдения из одной выбранной противоположности, будет выглядеть в нормированном к максимальной скорости обмена в виде уравнения:
![]() , (2)
, (2)
Перепишем полученное уравнение в ином виде:
![]() , (3)
, (3)
Далее произведем следующие преобразования:
| (4) |
Сделаем замену переменных и считаем, что m=1/v1, а m0=1/c. Иными словами учитываем обратно-пропорциональную связь противоположностей с представлением в ином виде. В итоге имеем:
![]() , (5)
, (5)
Если умножить оба члена указанного уравнения на величину c4 (что не меняет сути уравнения), то получим формулу энергии Эйнштейна в квадрате, которую изначально использовал Дирак при «линеаризации» и получении своей системы уравнений, что будет показано несколько ниже.
Соответственно мы видим, что значения скорости и массы выступают как противоположности связанные обратно пропорциональной связью и фактически заменяют соотношение неопределённостей Гейзенберга в детерминированном виде. Можно закон сохранения энергии Эйнштейна вывести и в ином известном представлении:
| (6) |
Учитывая, что в формулу энергии Эйнштейна входят только две переменные величины, которые дают замкнутую систему по формуле окружности, то они и являются противоположностями друг для друга (аналогично длине и времени, которые связаны через скорость света, что было впервые показано Минковским [2, с. 225-226]), т. е. могут преобразовываться только друг в друга. А отсюда следует, что указанные величины не могут выражаться через один и тот же вид в противоположных системах наблюдения, связанных через скорость света. Иначе такое преобразование ничем не зафиксировать в силу отсутствия различий между противоположностями. Однозначная связь скорости света (c) и постоянной Планка (h) была доказана в [1, с. 6-42] по формуле:
![]() , (7)
, (7)
Это с учётом необходимости смены представления объектов в противоположностях, означает необходимость записи m0=h=1/с. Повторим, мы вывели формулу энергии Эйнштейна из замкнутости двух противоположностей друг на друга на основе элементарной логики. Отсюда в формулу Эйнштейна входят только две переменные величины, которые дают замкнутую систему по формуле окружности, и они являются противоположностями друг для друга (аналогично длине и времени, которые связаны через скорость света r=ct [2, с. 225-226]), т. е. могут преобразовываться только друг в друга. В результате следует, что указанные величины не могут выражаться через один и тот же вид, иначе такое преобразование ничем не зафиксировать в силу отсутствия различий между противоположностями. Поэтому, если одна переменная величина выражает скорость v, то второй изменяемой переменной остаётся роль массы и при этом v1=1/m, а отсюда с учётом (7) и m0=h=1/с. Иными словами мы связали эти две величины друг с другом для объяснения формулы энергии Эйнштейна. При этом мы определили значение массы покоя электрона (позитрона) через величину обратно пропорциональную скорости света (обмена) и равную минимальной дискретной величине – постоянной Планка, и тем самым исключили представление массы вне описания через пространство и время, так как значение скорости определяется длиной и временем.
Отметим, что в представлениях физиков постоянная Планка и масса не имели связи с длиной и временем, а представлялись некими отдельными несвязанными величинами, выраженными в параметрах системы измерения, например СИ или СГС. Поэтому физики никак не могли вывести формулу энергии Эйнштейна из элементарной логики замкнутой системы на две глобальные противоположности. Отметим, что электрон и позитрон сохраняются вплоть до аннигиляции и меньше этих объектов с массой покоя просто быть не может, так как никакого другого дробного деления, с другим преобразованием, не обнаружено. Соответственно, представление величины объекта зависит от системы наблюдения в иерархии Мироздания при обратно-пропорциональной связи противоположностей, что было нами установлено в виде закона философии в [1, с. 6-42]. Из сказанного следует, что в качестве массы покоя в одной противоположности выступает скорость обмена в другой противоположности, то есть, иными словами, как это будет понятно далее, потенциальная энергия одной противоположности переходит в кинетическую энергию в другой противоположности. Отсюда, в общем следует, что масса покоя электрона (m0=h) характеризует в противоположности величину обменных процессов в объекте со скоростью света (с), и кинетическая энергия электрона в одной противоположности даёт массу покоя в другой противоположности с учётом обратно пропорциональной связи. Иное бы означало отсутствие противоположностей. То есть, то, что считается константой длины (массы) в одной противоположности представляется временем через скорость в другой противоположности. Собственно, это позволяет исключить парадокс сингулярности в ОТО Эйнштейна, так как разделение объектов одной противоположности осуществляется за счёт объектов другой противоположности, и если одни объекты отображают статику, то противоположные объекты выражают динамику обмена.
Следует также отметить, что перенос значения v2, из левой части уравнения (2) от знака равенства в правую часть от знака равенства в (3), привёл также и к смене закономерностей. А это означает, что в физике, в отличие от математики, не только нельзя произвольно переставлять переменные интегрирования или дифференцирования, но и делать произвольно перенос членов из одной части равенства в другую, так как с этим переносом надо учесть и изменение представления с учётом смены места наблюдения, а значит и закономерностей. Собственно, это связано с тем, что меняется принцип взаимодействия между противоположностями, когда сложение меняется на вычитание, и наоборот. И это также не учитывали физики и математики.
Надо отметить, что из общей формулы Мироздания также следует и необходимость описания пространства и времени через СТО и ОТО Эйнштейна.
Отметим, что Эйнштейн своим постулатом о постоянстве скорости света фактически интуитивно узаконил наличие двух противоположностей бытия и небытия как систем со своими пространственно-временными соотношениями (зависимыми и независимыми частями), где в результате движения происходят количественные изменения между этими системами. Однако, так как А. Эйнштейн не знал принцип построения мироздания от простого к сложному по логике на основе глобальных противоположностей, то он рассматривал необходимость существования СТО и ОТО исходя из исключения парадоксов в законах физики в зависимости от системы наблюдения. При этом он считал сами законы физики постулатами. Такой подход привёл его к противоречивым выводам, когда по СТО требуется относительность систем отсчёта с определением значения скорости, а в ОТО не обойтись без абсолютной системы отсчёта относительно которой будут измеряться скорости движения. Поэтому мы вначале займёмся рассмотрением общих принципов СТО и ОТО Эйнштейна, так как здесь имеется противоречивость используемых доказательств, которая потом привела к наличию космологических уравнений, чёрных дыр, телепортации, сил гравитации, ядерных сил и прочих алогизмов. Сложность восприятия СТО и ОТО заложена в том, что пространство и время нами, из жизненного опыта, воспринимаются как независимые величины. При этом считается, что существует [3, с.2-10]:
- Однородность пространства и времени;
- Изотропность пространства;
- Принцип относительности, то есть полное равноправие всех инерциальных систем отсчёта;
- Постулат постоянства скорости света, т. е. одинаковость скорости света во всех инерциальных системах отсчёта.
Действительно, механика убеждает в полном равноправии всех инерциальных систем отсчёта, что нашло своё отражение в известном принципе относительности Галилея. Принцип относительности Галилея опирается на два основных допущения [4, с. 199]:
- Время является абсолютным, то есть, единым для всех инерциальных систем отсчёта;
- Скорости складываются как евклидовы векторы, то есть, мы имеем евклидово пространство, где объект описывается по трём независимым друг от друга координатам.
В этом случае, пространство и время имеют независимость друг от друга. При этом мы имеем для пространства три также независимых друг от друга ортогональных направления.
Из этих допущений вытекают известные преобразования Галилея, связывающие между собой две инерциальные системы отсчёта, например, если одна из них движется относительно другой по одной из осей со скоростью v, то имеем уравнение движения в виде:
![]() , (8)
, (8)
Соответственно скорости систем отсчёта складываются и вычитаются по соответствующим ортогональным координатам.
Как известно, уравнения механики Ньютона для замкнутой системы материальных точек с массами mi, между которыми действуют силы Fik(i≠k), зависящие от относительных расстояний, можно представить:
| (9) |
Отсюда, мы замечаем, что ускорения точек, а также относительные расстояния являются инвариантами преобразований Галилея, так как скорость не входит в формулу наличия сил:
![]() , (10)
, (10)
В итоге уравнения (9) инвариантны относительно этих преобразований. Однако, в случае действия произвольных сил уравнения Ньютона только ковариантные (понятие ковариантности будет раскрыто несколько ниже) по отношению к преобразованиям Галилея и неинвариантные силы следует при этом рассматривать как внешние, то есть механическую систему нельзя считать замкнутой.
Что касается уравнений электродинамики Максвелла-Лоренца, то они по мнению учёных оказались не ковариантными относительно преобразований Галилея, а все попытки получить желанную ковариантность, как-то изменив форму уравнений, не принесли успеха, ибо приводили к противоречию с опытом. Например, появление полной силы Лоренца было связано с наличием разности скорости движения в инерциальных системах отсчёта:
![]() , (11)
, (11)
Понятно, что в отличие от (10), где силы определяются ускорением, здесь есть сила, связанная именно с наличием движения со скоростью v одной инерциальной системы относительно другой инерциальной системы. Но парадокс здесь возникал ещё и в том, что сила Лоренца рассматривалась относительно неподвижной системы отсчёта, а как тогда быть с представлением этой силы в подвижной инерциальной системе? Выходило, что при размещении наблюдателя на движущемся объекте vx=0, и при Bz=B0z, никакой силы просто быть не может, а это означало, что законы физики в подвижной и неподвижной инерциальной системе отличаются друг от друга, чего на практике не наблюдалось. Ещё один алогизм, связан с тем, что при скорости vx, есть наличие силы перпендикулярной радиальной силе Кулона. Проблема решается, если учитывать тот факт, что значение B0z от неподвижной системы это уже не величина Bz=B0z, то есть, представлять B0z, в подвижной системе аналогично так же, как и в неподвижной системе неправильно. Учитывая формулу (11), магнитная индукция от неподвижной системы преобразуется в электрическую силу взаимодействия инерциальных систем (объектов) в виде Еу= [vxB0z]/c. То есть, фактически магнитная индукция в неподвижной инерциальной системе выглядит напряжённостью электрического поля в подвижной инерциальной системе. Собственно, это явление получило название электромагнитного континуума (то есть, мы имеем аналог с пространственно-временным континуумом). Фактически закон Лоренца исключает существование первого закона Ньютона, то есть ни один объект мироздания нельзя представлять через инерциальную систему, которое имеет полностью замкнутое независимое состояние, так как всегда есть движение (изменение) относительно чего-либо. То есть, всякое тело (объект) не может находиться в состоянии покоя или равномерного и прямолинейного движения, и объект всегда будет испытывать ускорение, связанное с наличием силы Лоренца – Кулона. При этом наличие силы всегда связано с ускорением и изменением состояния объекта. Собственно, это подтверждается и формулами Луи де Бройля, где как движущемуся объекту и неподвижному объекту приписывается волновой процесс на основе функции Луи де Бройля. Отметим, что наличие волнового процесса, как это будет показано ниже, всегда связано с поглощением и излучением, что связано с изменением параметров самой частицы, и иное кстати бы исключало необходимость обмена и взаимодействия. Иными словами, всегда есть объекты, относительно которых выбранный объект имеет движение, а электромагнитные силы присущи любому объекту мироздания, и в отличие от описания неких неизвестных сил по механике Ньютона, мы должны рассматривать конкретные силы. Отсюда, необходимо было разобраться с причиной образования самих сил, что обеспечивает взаимосвязь всех объектов мироздания. Однако, проблему вначале предложили решить за счёт существования некоего электромагнитного эфира, что оправдывало не ковариантность (различный вид уравнений в подвижной и неподвижной системе отсчёта), и в этом случае уравнения Максвелла-Лоренца могут быть справедливыми лишь в единственной системе отсчёта, связанной с эфиром (то есть, таким образом вводилась абсолютная система отсчёта). Во всякой другой системе отсчёта эфир будет двигаться, а это должно сказаться на уравнениях поля. Иначе говоря, в любой «эфирной» теории предполагается существование «эфирного ветра», а это означает, что в уравнениях поля должна содержаться в качестве параметра скорость рассматриваемой системы отсчёта относительно эфира. Таким образом, представление об эфире оказывается несовместимым с принципом относительности Галилея, в чём наглядно убеждает следующий мысленный эксперимент.
Рассмотрим электромагнитную волну, порождаемую точечным источником света в момент времени t=0, и выясним, как будет выглядеть её распространение в двух инерциальных системах отсчёта, движущихся друг относительно друга со скоростью v. Пусть, скажем, система Σ связана с неподвижным эфиром, а система Σ* движется вдоль оси Х со скоростью v, так что в момент t=0, их начала отсчёта совпадают с положением источника.
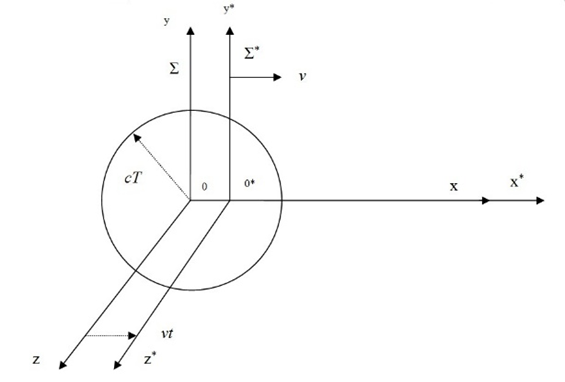
Рис. 1. Представление подвижной и неподвижной систем отсчёта относительно фронта волны
Тогда в момент t=T>0 свет достигнет точек, расположенных на расстоянии R=cT от начала координат r=0. Поэтому в системе Σ уравнение фронта волны имеет вид:
| (12) |
Необходимо отметить, что первое уравнение электромагнитной волны в (12) относится к чисто волновым процессам без корпускулярных свойств, а вот второе уравнение в (12) можно отнести к движению фотона вдоль оси z, и этот вид соответствует общей формуле Мироздания (1). Соответственно по осям х и у мы имеем вращательное круговое замкнутое движение, так как при х=0 и у=0 мы вообще не будем иметь объект, а в варианте первого уравнения фотон будет иметь распад. Это представление имеет связь с общей формулой Вселенной (1) в любой системе координат. Однако продолжим, и в системе Σ* к моменту t=T положение источника сместится вдоль оси Х на отрезок – vT и уравнение той же волновой поверхности примет вид (рис. 1):
![]() , (13)
, (13)
Таким образом, в системах Σ и Σ* уравнение волнового фронта выглядит по-разному. Но, как хорошо известно, из теории дифференциальных уравнений в частных производных, волновая поверхность является характеристической, и её вид определяется только коэффициентами соответствующих уравнений. Поэтому уравнения электромагнитного поля, в результате решения которых и получаются соответствующие волновые фронты (12) и (13), также должны выглядеть по-разному (иными словами, уравнение электромагнитной волны должно иметь член, учитывающий скорость движения), что говорит об их не ковариантности. Итак, «эфирная» концепция электромагнитного поля отрицает принцип относительности Галилея и допускает возможность опытного обнаружения эфирного ветра. Поэтому был поставлен опыт Майкельсона по обнаружению движения эфира относительно движения Земли [5, с. 201], исходя из того, что эфир должен иметь направленный вектор скорости его движения. Однако обнаружить эфирный ветер не удалось, что послужило основанием для сомнений в справедливости «эфирной концепции». Кроме того, мы отметим, что в эфирной концепции магнитная составляющая в формуле (11) остаётся неизменной в любой системе отсчёта и связана с наличием эфира. Отсюда нет относительности представления магнитных и электрических компонент в зависимости от движения, то есть, нет электромагнитного континуума. И таким образом, выбором системы отсчёта при vx=0, и при Bz=B0z, можно убрать силу Лоренца, а это означает, что законы физики зависят от системы отсчёта, что на практике не наблюдается. Отсюда необходимость возврата к принципу относительности и утверждению, что электромагнитные явления описываются одними и теми же уравнениями Максвелла-Лоренца во всех системах отсчёта, что было осознано Эйнштейном в его специальной теории относительности (СТО).
Как известно, в основу СТО было положено утверждение Эйнштейна (постулат) о постоянстве скорости света в любой инерционной системе отсчёта (принцип относительности), это фактически означает, что законы физики не зависят от инерциальной системы отсчёта, а любой физический закон связан с законом сохранения энергии (количества), иначе чудо возникновения из ничего. То есть, для наблюдателя, находящегося в подвижной системе, законы физики точно такие же, как и для наблюдателя находящегося в другой системе отсчёта, и в этом случае, не ясно, какую систему считать подвижной (всё относительно), а какую нет. Если исходить из концепции электромагнитного эфира, опирающейся на преобразования Галилея, то постулаты Эйнштейна представляются противоречивыми. Чтобы убедиться в этом, достаточно рассмотреть мысленный опыт со светом. В самом деле, фронт световой волны в системе Σ в момент времени t=T будет иметь вид сферы радиуса R=cT с центром в точке r=0. Однако в системе Σ* фронт той же самой световой волны должен, согласно постулату Эйнштейна, изображается сферой того же радиуса cT, но с центром в точке r*=0* (рис. 2). Таким образом, волновые фронты одной и той же световой волны в разных системах отсчёта не совпадают (нет одновременности событий). На первый взгляд, кажется, что для разрешения этого «очевидного» противоречия нужно либо отказаться от принципа постоянства скорости света, то есть, считать, что законы физики различны для инерционных систем, и тогда скорость света зависит от скорости движения источника, либо вновь вернуться к «эфирной» концепции. Разрешение противоречий, по мнению учёных, лежит во внимательном рассмотрении парадокса, и предположении, что причина его возникновения лежит в неявном использовании укоренившегося в нашем сознании представлении об абсолютном времени. То есть, о представлении времени в виде линейной неизменной величины (по сути дела это неизменная константа, которая фактически замкнута сама на себя), когда мы молчаливо полагаем t*=t и отождествляем принцип относительности с требованием ковариантности по отношению к преобразованиям Галилея.
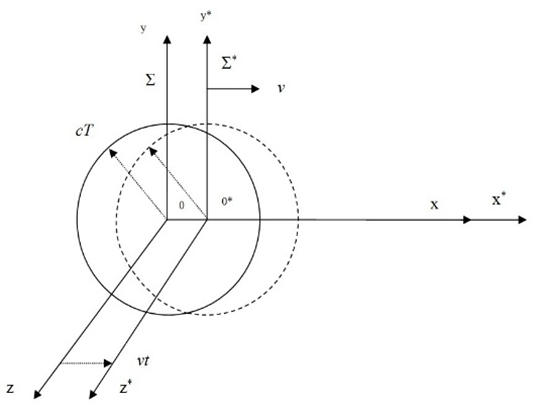
Рис. 2.
В этом случае надо отказаться от условия t*=t и считать, что t*=f(t,x), как это было предложено Лоренцем. Тогда становится очевидным, что окружности распространения электромагнитной волны от систем отсчёта Σ* и Σ, при выполнении законов физики в любой инерциальной системе отсчёта, не должны совпадать в силу относительности понятия движения со скоростью v. Иными словами одновременности событий в системах отсчёта Σ* и Σ из-за движения со скоростью v относительно друг друга – нет. Исходя из соблюдения принципа относительности, с выполнением законов физики, были выведены преобразования Лоренца в виде:
| (14) |
Обратные преобразования получаются заменой v на -v:
| (15) |
В этом случае получается, что движущееся тело сокращается в направлении своего движения по закону:
![]() , (16)
, (16)
При этом ход часов (времени) замедляется:
![]() , (17)
, (17)
Практически мы имеем как изменение времени, так и изменение длины, то есть, помимо t*=f(t,x), есть также и зависимость х*=f(t,x). Соответственно, мы имеем инвариантность в виде:
![]() , (18)
, (18)
В результате оказывается, что преобразования Лоренца соответствуют замкнутому взаимодействию двух глобальных противоположностей, так изменение аргумента v не влияет на произведение двух противоположных величин – длины и времени, и это означает пространственно-временной континуум. Действительно, в этом можно убедиться, так как преобразования Лоренца однозначно связаны с уравнением окружности. Покажем это, и с этой целью возведём формулу (16) в квадрат:
![]() , (19)
, (19)
Далее, мы можем записать:
![]() , (20)
, (20)
В этой формуле записи нет размерности, и величины выступают как количественные параметры противоположностей, а в динамике – как закономерности, так как только в случае закономерностей можно поддерживать при числовых изменениях указанное равенство. Легко увидеть, что данное равенство соответствует известной формуле окружности через закономерности.
Собственно указанные преобразования Лоренца на самом деле говорят, что представление объектов определяется связью их в системах отсчёта, так как длина и время определяют объект своими взаимными изменениями. А это на самом деле означает, что при условии закона сохранения количественного внешнего обмена внутреннее представление зависит от системы отсчёта. Иными словами, от системы отсчёта зависит и корпускулярно-волновое представление. Если мы бы взяли для аналогичного преобразования уравнение (17), то в этом случае мы бы обнаружили, что длина и время по отношению друг к другу выступают через аргумент по отношению к скорости в виде обратно-пропорциональной связи. Если сделать замену переменных в (20), и вместо v/c ввести аналогичный параметр vl0/(cl0)=t0/t, то получим:
![]() , (21)
, (21)
Можно продолжить замену переменных, что часто используется в квантовой механике. Для этого член l2/l02, умножим на член t02/ t02, а член t02/ t2 на l02/l02. В итоге с учётом l02/ t02=c2, и l2/ t02=v2, l02/ t2=v12, получаем уравнение окружности. Ортогональность величин v и v1 не вызывает сомнений, так как изначальными переменными были длина и время.
Формула энергии Эйнштейна также напрямую соответствует и выражению через гиперболические функции косинуса и синуса. Действительно, учитывая классическое релятивистское соотношение между массой и энергией, можно записать:
![]() , (22)
, (22)
Сопоставив с формулой (1), имеем:
![]() , (23)
, (23)
Отсюда получаем известную инвариантную форму, которая имеет вид:
![]() , (24)
, (24)
Учитывая, что длина и время объектов связаны преобразованиями Лоренца – Минковского с условием закона сохранения количества между глобальными противоположностями, следует вывод о неоднородности пространства и времени объектов в зависимости от скорости взаимодействия каждого объекта с другими объектами, то есть от скорости обмена (движения, изменения). Действительно, мы рассматриваем обмен как бы между двумя объектами мироздания (системами отсчёта), которые имеют отличие между друг другом благодаря скорости движения (изменения) одного объекта относительно другого. Других отличий нет, и в противном случае при отсутствии движения объектов в мироздании мы имеем однородность без возможности выделения, то есть мы имеем один общий объект. Если бы не было преобразований Лоренца – Минковского, то данные объекты были бы независимы, и связать два объекта через взаимодействие было бы невозможно, так как обмена между ними с условием закона сохранения количества было бы не получить (законы физики зависели бы от системы отсчёта). Как мы уже писали ранее в [1, с. 6-42], нет обмена – нет и взаимодействия! В данном случае скорость движения выступает фактором различия объектов друг от друга, которая, собственно, и приводит к неоднородности пространства и времени. Однако факт неоднородности объектов означает также и неоднородность окружающего пространства и времени, так как объекты имеют выражение через пространство и время, и если бы они такого выражения не имели, то были полностью независимы и замкнуты сами на себя без возможности их обнаружения в пространстве и времени, а значит и в Мироздании. Но, в чём выражается неоднородность окружающего объекты пространства и времени, мы ведь не наблюдаем движения пространства относительно её самой? И вот тут Эйнштейн решил выразить неоднородность пространства и времени через так называемые гравитационные силы. Отсюда, следующим постулатом Эйнштейна, который был положен в основу ОТО, было утверждение, что масса инерционная равна массе гравитационной. Этот вывод Эйнштейн обосновывал тем фактом, что наблюдатель в закрытом лифте не может выявить разницу в формировании ускорения, то есть, связано это ускорение с гравитационным ускорением, под действием, так называемых, сил тяжести (гравитационных сил), или с ускорением от приложения некоторой внешней силы, которая связывается с инерционной массой. Понятно, что понятие массы в данном случае также не определено (аналогично понятию заряда), в итоге было сделано деление массы на гравитационную и инерционную, и было высказано мнение, что это нечто такое содержащееся в пространственно-временном поле. Отсюда кстати и пошло понятие существования материи в пространстве и времени, и Эйнштейн вывел своё космологическое уравнение с исключением участия электромагнитных сил в виде общего ковариантного уравнения поля гравитации [6, с. 134]:
![]() , (25)
, (25)
Здесь ![]() – тензор Риччи, получающийся из тензора кривизны пространства и времени посредством свёртки его по паре индексов, R – скалярная кривизна, то есть свёрнутый тензор Ричи, составленный из связностей – производных метрического тензора
– тензор Риччи, получающийся из тензора кривизны пространства и времени посредством свёртки его по паре индексов, R – скалярная кривизна, то есть свёрнутый тензор Ричи, составленный из связностей – производных метрического тензора ![]() ,
, ![]() – тензор плотности энергии «обычной» материи (тензор энергии-импульса материи),
– тензор плотности энергии «обычной» материи (тензор энергии-импульса материи), ![]() – космологический член, который введён для учёта противодействия гравитации, G – гравитационная постоянная. Формула (25) представляет собой нелинейное уравнение, приводящее к невозможности использования при её решении принципа суперпозиции, что соответствует электромагнитному взаимодействию. Фактически это уравнение статического потенциального поля, так как здесь отсутствует динамика и не решена проблема сингулярности (разрывов). Соответственно решить проблему взаимодействия электромагнитных и так называемых гравитационных сил на основе этого уравнения не представляется возможным (нет обмена с взаимным превращением), хотя Эйнштейн потом и пытался создать теорию единого поля по связи гравитационных и электромагнитных сил в течение последних его 30 лет. Здесь при наличии пространственно-временного искривления встаёт вопрос о взаимодействии этого нечто в виде массы (материи) в этом пространственно-временном поле, так как отсутствие взаимодействия означает невозможность и обнаружения этого нечто (массы). Единственно известный способ взаимодействия связан с обменом, а тогда есть вопросы: «С чем связан этот обмен? Как осуществляется взаимное превращение массы (материи) в пространство и время, и наоборот, и какова его необходимость?» Собственно решение уже фактически было, так как равенство гравитационных и инерционных масс позволило Эйнштейну интерпретировать массу через пространственно-временное искривление на основе скорости движения относительно некоторой общей начальной абсолютной системы отсчёта, и это решало проблему возникновения массы. Однако, что представляет эта абсолютная система отсчёта, и с чем она связана физически, если по первому постулату всё относительно? По сути, получается, что ОТО опровергает СТО, так как ОТО требует единой общей системы отсчёта, относительно которой необходимо мерить элементарные скорости элементарных объектов для оценки пространственно-временного искривления, а в СТО такой системы принципиально быть не может, иначе законы физики должны быть разные в зависимости от системы отсчёта. Проблема решается, если учесть, что мироздание делится на две глобальные противоположности (в физике это интерпретируется как длина и время, а в философии как бытие и небытие), которые замкнуты друг на друга через обмен со скоростью света. Собственно постулат Эйнштейна о постоянстве скорости света (обмена) автоматически следует из нашей теории о замкнутости мироздания на две глобальные противоположности с выполнением закона сохранения количества. Связь противоположностей через скорость света также ввели не мы, а это сделано до нас в соответствии с геометрией Минковского по формуле r=ct [2, с. 225-226]. Так что Эйнштейну надо было понять наличие необходимости двух глобальных противоположностей, имеющих симметрию по количеству и определяющих две противоположные системы наблюдения, и тогда понятие массы вытекало бы как у нас по формулам (4) и (5) из значения скорости в противоположности с учётом обратно пропорциональной связи. Ранее в статье [7, с. 9-45] было показано, что сила Лоренца имеет составляющую, связанную со скоростью движения именно благодаря соответствию уравнению окружности как сила противодействия на действие силы Кулона. Таким образом, СТО и ОТО Эйнштейна отражают один и тот же закон замкнутости мироздания с учётом изменений, но в двух глобальных противоположностях, при этом никакого «эфирного ветра» быть не может, так как любое изменение по проекциям координатам длины преобразуется в проекцию времени со скоростью света, и наоборот, то есть направления «эфирного ветра» нет. Отсюда, выражение пространственно-временного искривления в виде взаимодействия объектов через обмен со скоростью света исключает необходимость эфира, который имеет свои параметры движения с наличием так называемого «эфирного ветра». Следовательно, ошибка физиков состояла в том, что они рассматривали эфир как однородный элемент со своим параметром скорости, а в реальности это пространственно-временное искривление – это взаимодействие противоположных объектов мироздания. Соответственно, в одной глобальной противоположности скорость отражает кинетическую энергию, а в другой глобальной противоположности потенциальную энергию через массу покоя в зависимости от системы наблюдения, что мы выше и показали. Понятно, что любой объект в мироздании должен характеризоваться через потенциальную и кинетическую энергию (иначе он выпадает из мироздания), при этом должна быть динамика обмена с переходом кинетической энергии в потенциальную, и, наоборот, с условием закона сохранения количества. Без обмена объекты друг для друга не существуют. Собственно, на этом построено формирование объекта в виде корпускулярных и волновых составляющих. Кроме того, законы физики должны быть в противоположностях аналогичны, так как иначе в результате неравенства закономерностей одна из глобальных противоположностей должна исчезнуть.
– космологический член, который введён для учёта противодействия гравитации, G – гравитационная постоянная. Формула (25) представляет собой нелинейное уравнение, приводящее к невозможности использования при её решении принципа суперпозиции, что соответствует электромагнитному взаимодействию. Фактически это уравнение статического потенциального поля, так как здесь отсутствует динамика и не решена проблема сингулярности (разрывов). Соответственно решить проблему взаимодействия электромагнитных и так называемых гравитационных сил на основе этого уравнения не представляется возможным (нет обмена с взаимным превращением), хотя Эйнштейн потом и пытался создать теорию единого поля по связи гравитационных и электромагнитных сил в течение последних его 30 лет. Здесь при наличии пространственно-временного искривления встаёт вопрос о взаимодействии этого нечто в виде массы (материи) в этом пространственно-временном поле, так как отсутствие взаимодействия означает невозможность и обнаружения этого нечто (массы). Единственно известный способ взаимодействия связан с обменом, а тогда есть вопросы: «С чем связан этот обмен? Как осуществляется взаимное превращение массы (материи) в пространство и время, и наоборот, и какова его необходимость?» Собственно решение уже фактически было, так как равенство гравитационных и инерционных масс позволило Эйнштейну интерпретировать массу через пространственно-временное искривление на основе скорости движения относительно некоторой общей начальной абсолютной системы отсчёта, и это решало проблему возникновения массы. Однако, что представляет эта абсолютная система отсчёта, и с чем она связана физически, если по первому постулату всё относительно? По сути, получается, что ОТО опровергает СТО, так как ОТО требует единой общей системы отсчёта, относительно которой необходимо мерить элементарные скорости элементарных объектов для оценки пространственно-временного искривления, а в СТО такой системы принципиально быть не может, иначе законы физики должны быть разные в зависимости от системы отсчёта. Проблема решается, если учесть, что мироздание делится на две глобальные противоположности (в физике это интерпретируется как длина и время, а в философии как бытие и небытие), которые замкнуты друг на друга через обмен со скоростью света. Собственно постулат Эйнштейна о постоянстве скорости света (обмена) автоматически следует из нашей теории о замкнутости мироздания на две глобальные противоположности с выполнением закона сохранения количества. Связь противоположностей через скорость света также ввели не мы, а это сделано до нас в соответствии с геометрией Минковского по формуле r=ct [2, с. 225-226]. Так что Эйнштейну надо было понять наличие необходимости двух глобальных противоположностей, имеющих симметрию по количеству и определяющих две противоположные системы наблюдения, и тогда понятие массы вытекало бы как у нас по формулам (4) и (5) из значения скорости в противоположности с учётом обратно пропорциональной связи. Ранее в статье [7, с. 9-45] было показано, что сила Лоренца имеет составляющую, связанную со скоростью движения именно благодаря соответствию уравнению окружности как сила противодействия на действие силы Кулона. Таким образом, СТО и ОТО Эйнштейна отражают один и тот же закон замкнутости мироздания с учётом изменений, но в двух глобальных противоположностях, при этом никакого «эфирного ветра» быть не может, так как любое изменение по проекциям координатам длины преобразуется в проекцию времени со скоростью света, и наоборот, то есть направления «эфирного ветра» нет. Отсюда, выражение пространственно-временного искривления в виде взаимодействия объектов через обмен со скоростью света исключает необходимость эфира, который имеет свои параметры движения с наличием так называемого «эфирного ветра». Следовательно, ошибка физиков состояла в том, что они рассматривали эфир как однородный элемент со своим параметром скорости, а в реальности это пространственно-временное искривление – это взаимодействие противоположных объектов мироздания. Соответственно, в одной глобальной противоположности скорость отражает кинетическую энергию, а в другой глобальной противоположности потенциальную энергию через массу покоя в зависимости от системы наблюдения, что мы выше и показали. Понятно, что любой объект в мироздании должен характеризоваться через потенциальную и кинетическую энергию (иначе он выпадает из мироздания), при этом должна быть динамика обмена с переходом кинетической энергии в потенциальную, и, наоборот, с условием закона сохранения количества. Без обмена объекты друг для друга не существуют. Собственно, на этом построено формирование объекта в виде корпускулярных и волновых составляющих. Кроме того, законы физики должны быть в противоположностях аналогичны, так как иначе в результате неравенства закономерностей одна из глобальных противоположностей должна исчезнуть.
Однако как связать эти два противоположных свойства с учётом закона сохранения энергии по уравнению Эйнштейна?
2. Вывод системы уравнений Дирака из уравнения энергии Эйнштейна для описания корпускулярно-волнового дуализма. Логический смысл функций и формул Луи де Бройля.
Как показано выше, уравнение энергии Эйнштейна напрямую связано с замкнутостью противоположностей мироздания друг на друга с учётом элементарной логики с отсутствием чудес появления и исчезновения в ноль по формуле (1). Отсюда следует вывод, что и далее результат взаимодействия противоположностей в их динамике изменения при корпускулярно-волновом дуализме также должен соответствовать уравнению энергии Эйнштейна для остальных законов физики. В противном случае, при разрыве чудес не избежать. Поэтому, для описания взаимодействия противоположностей на основе корпускулярно-волнового дуализма Дирак интуитивно использовал уравнение энергии Эйнштейна в виде [8, с. 295-296]:
![]() , (26)
, (26)
Здесь k изменяется от 0 до 3; P0=M0c; P1=Px; P2=Py; P3=Pz. Из этой записи при использовании матриц для разложения (26):
| (27) |
Следуют известные линеаризованные уравнения:
| (28) |
Далее Дирак ввёл операторы Е и р [9, с. 298] с мнимой единицей:
![]() , (29)
, (29)
Которые должны воздействовать на волновую функцию Луи де Бройля Ψ, и которая, в свою очередь, характеризует вероятность. Необходимость использования таких операторов мы показали в [1, с. 6-42]. При этом волновые функции Ψ Луи де Бройля при соответствии уравнению энергии Эйнштейна имеют вид [10, с. 31]:
![]() , (30)
, (30)
В дифференциальном виде мы получим систему уравнений Дирака:
| (31) |
После соответствующей подстановки с выражением одних функций через другие Дираком для функции ![]() было получено решение:
было получено решение:
| (32) |
Соответственно получаем уравнение энергии Эйнштейна в квадрате с учётом функции ![]() :
:
![]() , (33)
, (33)
Иными словами, система уравнений Дирака при переходе в уравнение энергии Эйнштейна связана с умножением на волновую функцию Луи де Бройля, что обеспечивает корпускулярно-волновой вид. Собственно, в квантовой механике есть представление на основе релятивистского отображения уравнения энергии Эйнштейна с учётом операторов (29) и в чисто волновом виде [10, с. 31] при волновой функции вида:
![]() , (34)
, (34)
И уравнении:
![]() , (35)
, (35)
В этом случае в качестве решения при наличии массы покоя получается уравнение энергии Эйнштейна в квадрате, которое использовал Дирак в своей системе уравнений, и это не наша выдумка. Однако хоть Дираку и удалось отразить связь волновых свойств с корпускулярными свойствами с переходом к уравнению частицы по формуле энергии Эйнштейна, но он не смог отказаться от волновых функций Луи де Бройля, характеризующих вероятность, так как вид его уравнений не соответствовал виду обычных уравнений Максвелла с отображением реальных электромагнитных функций. Кроме того, волновой вид связан с распространением в окружающей среде электромагнитных волн, которые характеризуется константами электрической и магнитной проницаемости, а их в уравнении (35) нет (этот парадокс имеет и система измерения СГС). Иными словами, здесь нет влияния окружающей среды на волновое уравнение, а значит, нет соблюдения принципа Гюйгенса – Френеля с изменением направления движения за счёт вторичных источников возбуждения, так как масса покоя электрона (![]() ) – это константа. В итоге получилось, что система уравнений Дирака не имела логичного доказательства, соответствующего практике, а явилось своего рода математическим упражнением с подгонкой под результат. Собственно, это означает, что необходимо привести систему уравнений Дирака в вид, соответствующий реальным физическим законам с учётом взаимодействия реальных объектов. Соответственно мы помним, что система уравнений Дирака описывает замкнутый обмен между противоположностями объектов с учётом закона сохранения количества.
) – это константа. В итоге получилось, что система уравнений Дирака не имела логичного доказательства, соответствующего практике, а явилось своего рода математическим упражнением с подгонкой под результат. Собственно, это означает, что необходимо привести систему уравнений Дирака в вид, соответствующий реальным физическим законам с учётом взаимодействия реальных объектов. Соответственно мы помним, что система уравнений Дирака описывает замкнутый обмен между противоположностями объектов с учётом закона сохранения количества.
Так как вероятностные волновые функции не имеют реального воплощения, то, следовательно, необходимо определить, чем обмениваются объекты для взаимодействия для сохранения этих объектов в динамике, и как это должно быть выражено через математические уравнения.
При этом объекты для обмена, определяемые через математические уравнения, должны соответствовать объектам, наблюдаемым при практическом распаде масс по [11, с. 277] в виде:
| (36) |
Из (36) видно, что все распады на практике осуществляются через электронные и мюонные нейтрино (антинейтрино) ![]() с аннигиляцией частиц с превращением в фотоны
с аннигиляцией частиц с превращением в фотоны ![]() . При этом нет ни одного распада на гипотетические гравитоны, кварки, глюоны и виртуальные фотоны. Собственно, это подтверждает идею М. В. Ломоносова, что объект состоит из того, на что он распадается. Исходя из этого, следует предположить, что переход от одного состояния в другое связан с изменением взаимодействия между составляющими от элементов распада. Надо отметить, что по этому пути пошли и физики, когда приравняли массу покоя в системе уравнений Дирака (31) к нулю (
. При этом нет ни одного распада на гипотетические гравитоны, кварки, глюоны и виртуальные фотоны. Собственно, это подтверждает идею М. В. Ломоносова, что объект состоит из того, на что он распадается. Исходя из этого, следует предположить, что переход от одного состояния в другое связан с изменением взаимодействия между составляющими от элементов распада. Надо отметить, что по этому пути пошли и физики, когда приравняли массу покоя в системе уравнений Дирака (31) к нулю (![]() ) и посчитали, что тем самым они получают уравнения для электронных и мюонных нейтрино. При этом в квантовой механике для описания нейтрино и антинейтрино используется уравнение с двухрядными матрицами Паули (уравнение Вейля), либо система уравнений Дирака, с расщеплением на независимые уравнения [12, с. 355]:
) и посчитали, что тем самым они получают уравнения для электронных и мюонных нейтрино. При этом в квантовой механике для описания нейтрино и антинейтрино используется уравнение с двухрядными матрицами Паули (уравнение Вейля), либо система уравнений Дирака, с расщеплением на независимые уравнения [12, с. 355]:
| (37) |
Однако при этом для описания волновых процессов использовалась функция Луи де Бройля, которая характеризует вероятность. Соответственно скорость движения электронных и мюонных нейтрино и антинейтрино должна была быть постоянной и равной скорости света. Но, тогда говорить о наличии вероятности по волновым функциям при одной и той же скорости в принципе невозможно. При этом видно, что первое уравнение в (37) отличается от третьего уравнения в (37) только обозначением в названии функций, аналогично это относится и к второму и четвёртому уравнениям в (37). Отличие в названиях при одинаковом виде уравнений не может дать отличие в законах взаимосвязи, а значит и свойствах, так как решение всегда однозначное. Однако физики с целью исключения этого парадокса придумали деление на правую и левую материю и тем самым как бы решили парадокс деления на электронные и мюонные нейтрино и антинейтрино (рис. 3) добавив в названия обозначения на правое и левое нейтрино (антинейтрино).
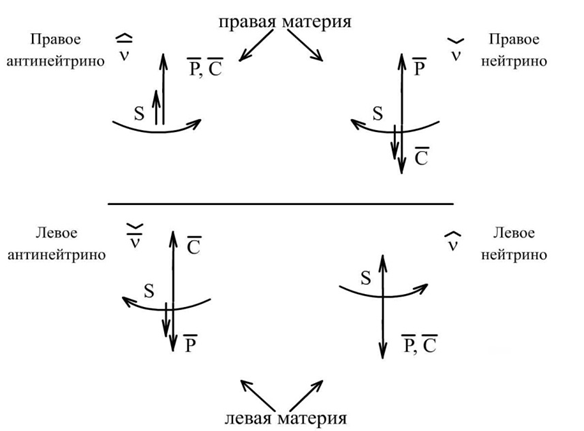
Рис. 3. Левые и правые нейтрино и антинейтрино
Понятно, что это приводит к новому парадоксу, связанному с отличием между правой и левой материей, и в чём их отличие, и как их обнаружить? Кроме того, по какой причине влияние внешнего объекта при одинаковом виде уравнений для частиц должно иметь различие, которое присуще электронным и мюонным нейтрино (антинейтрино) при взаимодействии? Соответственно не ясен в этом случае и процесс аннигиляции противоположно заряженных частиц, так как в процессе аннигиляции получаются электромагнитные волны с наличием констант электрической и магнитной проницаемости, а их в уравнениях в системе Дирака для нейтрино и антинейтрино нет! Иными словами, здесь нет взаимосвязи между электронными и мюонными нейтрино и антинейтрино и электромагнитными волнами на основе уравнений Максвелла. А это означает, что нейтрино и антинейтрино, в интерпретации системы уравнений Дирака, не могут дать электромагнитные волны с отсутствием при преобразовании массы покоя из-за распространения со скоростью света, и сам процесс аннигиляции в этом случае связан с чудесами. То есть, нет закона преобразования в системе уравнений Дирака из нейтрино и антинейтрино в электромагнитные волны. При этом нет связи электронных и мюонных нейтрино и антинейтрино с обычными уравнениями Максвелла, от которых есть закон перехода к уравнениям электромагнитных волн, что было показано в классической электродинамике. При этом был ещё один парадокс в силу того, что полученные уравнения электромагнитной волны не связаны с корпускулярными свойствами. Также понятно, что функция Луи де Бройля, которая характеризует вероятность, и используется в системе уравнений Дирака вообще отрицает наличие законов физики, так как случайность и закономерность – это противоположности. Чтобы разрешить указанные парадоксы, вспомним смысл выдвижения самой гипотезы Луи де Бройля [13, с. 216]. Луи де Бройль предположил, что со всякой неподвижной частицей массы , связан некоторый периодический процесс:
![]() , (38)
, (38)
Здесь ![]() – редуцированная постоянная Планка, а
– редуцированная постоянная Планка, а ![]() – постоянная Планка. Иначе говоря, он постулировал существование волнового поля, связанного с частицей:
– постоянная Планка. Иначе говоря, он постулировал существование волнового поля, связанного с частицей:
![]() , (39)
, (39)
Данная функция должна изменяться по гармоническому закону одновременно во всех точках пространства. Если же частица движется со скоростью v, то, считая поле ![]() скалярным, найдём, что в системе
скалярным, найдём, что в системе ![]() , связанной с частицей, поле де Бройля имеет вид:
, связанной с частицей, поле де Бройля имеет вид:
![]() , (40)
, (40)
Собственно, в формуле (40) уже заложен парадокс, так как есть движение частицы, а функция Луи де Бройля рассматривается так же, как и для элементарной частицы в состоянии покоя отдельно от движения, но с другими параметрами энергии, например вида ![]() . Практически это можно понять с точки зрения предлагаемой теории, так как физики интуитивно представили кинетическую энергию движения со скоростью v в виде массы покоя. Соответственно этот парадокс, физики в системе
. Практически это можно понять с точки зрения предлагаемой теории, так как физики интуитивно представили кинетическую энергию движения со скоростью v в виде массы покоя. Соответственно этот парадокс, физики в системе ![]() , решили исключить согласно преобразованиям Лоренца, и представили функцию Луи де Бройля в виде:
, решили исключить согласно преобразованиям Лоренца, и представили функцию Луи де Бройля в виде:
![]() , (41)
, (41)
Здесь: ![]() ,
, ![]() ,
, ![]() .
.
Однако в этом случае получилось, что слева от знака равенства функция Луи де Бройля связана с неподвижной частицей, а справа от знака равенства должно быть перемещение. Иными словами функция Луи де Бройля представляется неоднозначно, и с каждой движущейся со скоростью ![]() частицей, по мнению физиков, связано поле Луи де Бройля в виде плоской волны, изменяющейся по гармоническому закону, и распространяющейся в пространстве с фазовой скоростью u, определяемой соотношением:
частицей, по мнению физиков, связано поле Луи де Бройля в виде плоской волны, изменяющейся по гармоническому закону, и распространяющейся в пространстве с фазовой скоростью u, определяемой соотношением:
![]() , (42)
, (42)
Но, так как ![]() , то, собственно, это означает парадокс и получается, что волновая функция поля Луи де Бройля имеет иную скорость, чем частица. Если в рамках электродинамики в волноводе такая фазовая скорость имеет право на существование на основе отражения от границ волновода, то в открытом пространстве таких границ нет. Понятно, что здесь нет механизма получения замкнутого волнового поля, который позволяет совместить корпускулярные и волновые свойства в одном объекте как в покое, так и при движении. Из данного парадокса попытались выйти за счёт придания функциям Луи де Бройля вероятностный характер с нарушением СТО Эйнштейна. Отсюда кстати возникла гипотеза о существовании тахионов [14, с. 291]. Однако наличие гармонической закономерности противоречит наличию вероятности и требует для своего существования реальных сил, обеспечивающих этот гармонический процесс. Действительно, ранее на практике было получено, что связь между длинной волны Луи де Бройля и импульсом движущейся частицы следует из формулы Луи де Бройля [15, с. 62]:
, то, собственно, это означает парадокс и получается, что волновая функция поля Луи де Бройля имеет иную скорость, чем частица. Если в рамках электродинамики в волноводе такая фазовая скорость имеет право на существование на основе отражения от границ волновода, то в открытом пространстве таких границ нет. Понятно, что здесь нет механизма получения замкнутого волнового поля, который позволяет совместить корпускулярные и волновые свойства в одном объекте как в покое, так и при движении. Из данного парадокса попытались выйти за счёт придания функциям Луи де Бройля вероятностный характер с нарушением СТО Эйнштейна. Отсюда кстати возникла гипотеза о существовании тахионов [14, с. 291]. Однако наличие гармонической закономерности противоречит наличию вероятности и требует для своего существования реальных сил, обеспечивающих этот гармонический процесс. Действительно, ранее на практике было получено, что связь между длинной волны Луи де Бройля и импульсом движущейся частицы следует из формулы Луи де Бройля [15, с. 62]:
![]() , (43)
, (43)
Однако, математически эта формула может быть фактически получена из аргумента волновой функции Луи де Бройля ![]() , которая отражает условие, где количественные изменения в противоположностях равны. То есть изменения по времени равны изменениям в пространстве, что и обеспечивает перемещение волновой функции в соответствии с корпускулярным движением частицы. Отсюда имеем:
, которая отражает условие, где количественные изменения в противоположностях равны. То есть изменения по времени равны изменениям в пространстве, что и обеспечивает перемещение волновой функции в соответствии с корпускулярным движением частицы. Отсюда имеем:
| (44) |
Соответственно для движущегося объекта с характеристикой волновых свойств по формуле (41) условие сочетания корпускулярных и волновых свойств сохраняется при выполнении закона (43), если в системе наблюдения от неподвижной системы значение x/u=t. Но, скорости выше скорости света нет, поэтому здесь необходимо вспомнить, что формула энергии Эйнштейна Е/m=c2 выведена из подчинения замкнутой системе и аналогична закону по формуле (42) с разницей в обозначении переменных. Иными словами, в силу однозначности закона, значения u и v также отображают противоположности, замкнутые друг на друга и отличие лишь в замене обозначения переменных. Следовательно, с учётом выбранной системы наблюдения, так называемая фазовая скорость u должна отображать противоположность в виде массы по закону (u=1/m) с выполнением СТО и ОТО Эйнштейна и подчинением уравнению энергии Эйнштейна. Отсюда с учётом (5) и (6) имеем: x/u=mct0=cm0t0/(1-v2/c2)1/2=t. В предлагаемой теории [1, с. 6-42] cm0=сh=1. В итоге имеем соблюдение СТО Эйнштейна с разницей времени между подвижной и неподвижной системой наблюдения в виде:
![]() , (45)
, (45)
С учётом равенства (45) формула (41) в этом случае имеет вид:
![]() , (46)
, (46)
Здесь r=сt, E=hf, f=сv, а значение ![]() , должно характеризовать корпускулярные свойства в виде пространственно-временного искривления по СТО и ОТО Эйнштейна [2, с. 225-226] в соответствии с преобразованиями Лоренца – Минковского в виде:
, должно характеризовать корпускулярные свойства в виде пространственно-временного искривления по СТО и ОТО Эйнштейна [2, с. 225-226] в соответствии с преобразованиями Лоренца – Минковского в виде:
![]() , (47)
, (47)
Здесь значение w, согласно общей формуле мироздания (1), может определять эквивалент потенциальной энергии в замкнутой системе Мироздания на две глобальные противоположности. В этом случае общая функция Луи де Бройля ![]() характеризует корпускулярно-волновые свойства с подчинением СТО и ОТО Эйнштейна и подчинением формуле (1). Таким образом, мы установили, что смена системы наблюдения с неподвижной на подвижную не приводит к нарушению формулы Луи де Бройля (44), если учесть представление фазовой скорости u с учётом обратно-пропорциональной связи в виде массы в противоположной системе наблюдения и отображением аргумента функции через энергию и импульс. Если вспомнить, что в (41)
характеризует корпускулярно-волновые свойства с подчинением СТО и ОТО Эйнштейна и подчинением формуле (1). Таким образом, мы установили, что смена системы наблюдения с неподвижной на подвижную не приводит к нарушению формулы Луи де Бройля (44), если учесть представление фазовой скорости u с учётом обратно-пропорциональной связи в виде массы в противоположной системе наблюдения и отображением аргумента функции через энергию и импульс. Если вспомнить, что в (41) ![]() , то в соответствующей системе наблюдения будем иметь значение импульса в виде
, то в соответствующей системе наблюдения будем иметь значение импульса в виде ![]() . Иными словами, мы видим, что функция Луи де Бройля с учётом нормировки соответствует функции (30), которая была использована Дираком в его системе уравнений (31).
. Иными словами, мы видим, что функция Луи де Бройля с учётом нормировки соответствует функции (30), которая была использована Дираком в его системе уравнений (31).
При этом мы решили проблему парадокса фазовой скорости за счёт отличия представления объектов в противоположных системах наблюдения в соответствии с СТО и ОТО Эйнштейна со сменой кинетической энергии на потенциальную.
Собственно, сама идея перемещения волновой функции вместе с частицей была также предложена физиками, однако при описании этой волновой функции через функцию Луи де Бройля они столкнулись с парадоксом, связанным с фазовой скоростью u, что исключало перемещение волновой функции одновременно с движущейся частицей со скоростью v, при одинаковом представлении объекта в разных системах наблюдения. Отсюда и возникло предположение у физиков о связи функции Луи де Бройля с вероятностью. Этот парадокс фактически был разрешён в СТО и ОТО Эйнштейном, так как кинетическая энергия движения в одной системе наблюдения представляется потенциальной энергией пространственно-временного искривления в системе наблюдения связанной с первой через скорость света. Именно на основании этого закона мы смогли показать перемещение функции Луи де Бройля одновременно с частицей и также получить и саму формулу Луи де Бройля (43). Практически функция Луи де Бройля – это стоячая волна, обеспечивающая взаимодействие и обмен между противоположностями одного объекта с соблюдением закона сохранения количества.
Так как из функции Луи де Бройля по виду (46) получается формула Луи де Бройля (43), подтверждённая на практике экспериментально, то, соответственно, она должна отражать реальные силы, существующие в мироздании, которые имеют гармоническое изменение. На практике такие силы отражающие гармонические изменения выражаются через напряжённости электрических и магнитных полей. Более того, такие элементарные частицы как электрон и позитрон при аннигиляции дают фотоны – электромагнитные волны, да и сами эти частицы имеют собственное электрическое и магнитное поле. Это говорит о том, что корпускулярные свойства образуются за счёт электромагнитных составляющих, в замкнутом взаимодействии между противоположностями. Аналог можно представить в виде объёмного резонатора, где тоже происходит взаимодействие между корпускулярными и волновыми свойствами, но на основе разных объектов. Отсюда следует необходимость перехода от функции Луи де Бройля, которая по мнению физиков характеризует вероятность, к реальным электромагнитным составляющим с учётом законов физики, которые реально используются в классической электродинамике с целью описания корпускулярных свойств частиц.
Таким образом, мы пришли к следующим выводам:
- Отсутствие «эфирного ветра» связано с тем, что пространственно-временное искривление отражает взаимодействие через обмен объектов мироздания со скоростью равной скорости света. При этом объекты обмена должны распространяться со скоростью света и иметь электромагнитные волновые свойства. Наличие «эфирного ветра» означало бы взаимодействие со скоростью меньше, чем скорость света.
- Дирак исходя из уравнения энергии Эйнштейна смог показать связь волновых свойств с корпускулярными свойствами на основе волновых функций Луи де Бройля через свою систему уравнений. Однако сам вид этих уравнений не позволял их представить через обычные уравнения Максвелла с переходом к уравнению волны с учётом констант электрической и магнитной проницаемости. Поэтому он стал исходить из связи этих волновых функций с вероятностью.
- Полученный результат позволял описывать движение элементарных частиц типа электрона или позитрона, но для описания частиц с большей массой он был не пригоден.
- Система уравнений Дирака при описании через волновые функции Луи де Бройля, характеризующих вероятность, не даёт различий при описании электронных и мюонных нейтрино (антинейтрино) и не объясняет переход от противоположных частиц к фотонам при аннигиляции в силу того, что имеется совпадение вида уравнений и фактически четыре уравнения превращаются в два.
- Связь функции Луи де Бройля с её распространением с фазовой скоростью выше, чем скорость света противоречит СТО Эйнштейна. Решение этой проблемы связано через представление массы и скорости в зависимости от системы наблюдения как это показано выше.
- Исходя из отражения через функцию Луи де Бройля реального закона физики, проверенного на практике, следует выразить функцию Луи де Бройля через реальные гармонические функции электрических и магнитных полей, так как никаких иных гармонических функций на практике не наблюдается.
- Исходя из того, что, как это было показано выше, с помощью уравнений Дирака не удаётся описать электронные и мюонные нейтрино (антинейтрино), а также необходимо выразить функции Луи де Бройля через реальные электромагнитные составляющие, то отсюда следует необходимость выразить эти объекты через реальные процессы в электродинамике, используя уже полученные решения, которые соответствуют практике.
- Так как обычные уравнения Максвелла из классической электродинамики не соответствуют уравнениям Дирака, на основе которых получается связь корпускулярных и волновых свойств, то отсюда следует необходимость обоснования представления этих уравнений электродинамики в виде, соответствующем уравнениям Дирака с учётом соответствия реальным объектам, таким как электронные и мюонные нейтрино и антинейтрино.
3. Вывод усовершенствованных уравнений Максвелла исходя из известных уравнений в классической электродинамике и законов мироздания. Переход от усовершенствованных уравнений Максвелла к волновому виду.
На основании выводов, сделанных в предыдущем разделе, определим парадоксы, на основании которых возникла необходимость усовершенствования уравнений Максвелла для описания корпускулярно-волновых свойств.
То есть. это связано с тем, что обычные уравнения Максвелла в нынешнем их виде описывают только волновые свойства плоской электромагнитной волны как объекта, а, как известно, в начале ХХ века у электромагнитной волны были обнаружены корпускулярные свойства, что было продемонстрировано в опытах Лебедева по определению давления света (по сути, это подтверждение того, что любой объект мироздания выражается через корпускулярно-волновой дуализм). Это означало, что обычные уравнения Максвелла верны только в определенных пределах. Кроме того, основной парадокс, который не смогли объяснить физики, заключался в том, что в обычных уравнениях Максвелла энергия вычислялась строго от амплитуды напряженности электрических и магнитных полей и не зависела от частоты колебаний. В квантовой механике при переходе от волны к частице энергия излучения фотонов определяется от частоты колебательного процесса, т. е. не используются напряженности электрических и магнитных полей. Это видно по использованию функций Луи де Бройля в системе уравнений Дирака, где энергия в аргументе функции связана с частотой. Этот парадокс на основе обычных уравнений Максвелла решить (в рамках существующих теорий) физики не смогли, так как при описании только волновых свойств нет механизма связи частоты и напряженности. Понятно, что измерять напряженности электрических и магнитных полей для волн длиной в микроны невозможно. Поэтому возникает проблема измерения электромагнитных компонент Е и Н в зависимости от частоты и разрешить ее без привлечения противоположностей не представляется возможным. Так, в обычных уравнениях Максвелла частота входит в аргумент функции, но не влияет на расчеты энергии, хотя описывает волновой характер движения волны. С другой стороны, по практическим результатам, фотоны имеют по своим свойствам явно выраженный корпускулярный характер, но их энергия зависит от частоты, то есть от волновых свойств. Собственно, отсюда и следует известная формула Луи де Бройля, в которой отражены связь частоты и массы [13, с. 216]:
![]() , (48)
, (48)
Кроме того, связь ортогональных (перпендикулярных по геометрии) величин напряженностей электрических и магнитных полей хотя и следовала из практических опытов Фарадея, но любой математик знает, что ортогональные величины должны быть независимы. И здесь связь ортогональных величин принимается как постулат, следующий из практических данных. Однако волновые уравнения плоских волн напряжённостей электрических и магнитных полей, которые выведены из обычных уравнений Максвелла никак не связаны математически и такой парадокс физики с математикой очевиден и тоже подлежит объяснению. Можно также заметить и парадоксы представления электромагнитной волны при графическом изображении, так, на рисунке 4. мы видим, что есть участки по краям, где силовые электрические и магнитные напряжённости электромагнитного поля направлены не ортогонально (перпендикулярно) направлению движения, а параллельно направлению движения волны со скоростью света. Кроме того, для получения силового воздействия, например, для напряжённости того же статического электрического поля, необходимо наличие разности потенциалов, но при замкнутой силовой линии его просто быть не может, так как должен быть участок с обратным направлением напряжённости для потенциалов.
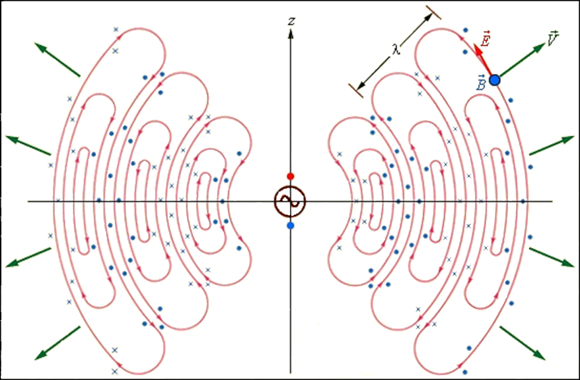
Рис. 4. Изображение электромагнитной волны в динамике излучения
Аналогично мы видим парадокс и в отображении плоской электромагнитной волны по рисунку 5.
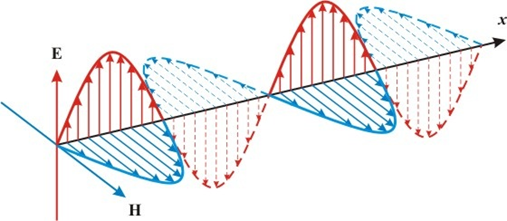
Рис. 5. Электромагнитная волна в изображении в плоскости осей координат
Здесь необходимо предположить, что вектора напряжённостей электрических и магнитных полей должны иметь и начало, и конец. А это означает наличие зарядов (или то, что должно характеризоваться как противоположные объекты для взаимодействия), для создания разности потенциалов, как для электрического поля, так и для магнитного поля. Но это означает отсутствие различий между электрическими и магнитными составляющими, а значит, нет и противоположностей. Противоречие с рисунком 4 по наличию непрерывной линии одной величины напряжённости видно также по рисунку 6.
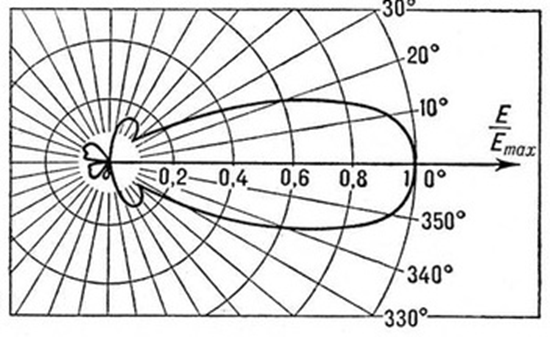
Рис. 6. Излучение электромагнитного поля антенной
Здесь видно, что в зависимости от углового направления меняется напряжённость и энергия электромагнитного поля. Понятно, что это противоречит замкнутости силовой линии одной величины напряжённости по рисунку 4 и требует преобразования электромагнитного поля в пространственно-временное искривление и, наоборот, в противном случае было бы чудо исчезновения в ничто и появления из ничего. Иными словами, получить полную замкнутость только на основе одного вида представления объекта в виде, например напряжённости поля не удаётся. Таким образом, мы видим, что упрощённое описание электромагнитного взаимодействия по рисункам даёт парадоксы. Попытаемся выявить эти парадоксы более детально на основе известных законов физики и представить варианты решения без парадоксов с учётом наших выведенных законов и теории мироздания в соответствии с элементарной логикой [1, с. 6-42].
Отсюда, рассмотрим три известных закона физики по электродинамике которые рассматриваются как постулаты, и попытаемся от них прийти к описанию наипростейших объектов, так как законы физики должны выполняться и для простейших объектов, иное бы означало разрыв в схеме и логике от простого к сложному.
Первый известный закон физики, проверенный на практике – это дифференциальный закон Фарадея, по которому изменение магнитного поля вызывает замкнутое электрическое поле, и математически это выражается в виде формулы [16, с. 46]:
![]() , (49)
, (49)
Замкнутое электрическое поле здесь потому, что в противном случае в замкнутом проводнике был бы не ток при изменении магнитного поля, а поляризация зарядов. Понятно, что сейчас мы не рассматриваем вариант самого формирования замкнутости силовой линии, а просто представляем процесс дающий результат в виде замкнутой величины тока и отображаем это как вектор напряжённости электрического поля (в дальнейшем нам будет понятно, какой процесс приводит к замкнутости).
Второй известный закон физики, тоже проверенный на практике это закон, по которому движение электрического заряда (а по сути ‒ это есть изменение во времени электрического поля) вызывает замкнутое магнитное поле; этот закон выражается в виде формулы:
![]() , (50)
, (50)
Однако, как заметили сами физики, уравнение (50) не может быть справедливым [17, с. 28], так как по мнению физиков в нестационарном случае из него следует ![]() , тогда как согласно уравнению непрерывности мы имеем:
, тогда как согласно уравнению непрерывности мы имеем:
![]() , (51)
, (51)
В этом случае с математической точки зрения противоречие исчезает только в стационарном пределе, когда ![]() . Поэтому физики посчитали, что уравнение (50) необходимо обобщить, добавив некоторый вектор, исчезающий в стационарном случае, т. е. вектор вида
. Поэтому физики посчитали, что уравнение (50) необходимо обобщить, добавив некоторый вектор, исчезающий в стационарном случае, т. е. вектор вида ![]() , названный Максвеллом током смещения:
, названный Максвеллом током смещения:
![]() , (52)
, (52)
Приняв во внимание (50), получили:
![]() , (53)
, (53)
Учитывая дифференциальную форму Гаусса для напряжённости электрического поля, мы имеем:
![]() , (54)
, (54)
Отсюда следует запись:
![]() , (55)
, (55)
Исходя из (55) путем замены ![]() на
на ![]() , физики получают уравнение:
, физики получают уравнение:
![]() , (56)
, (56)
Однако добавочный (фиктивный) ток смещения ![]() никак не может быть отражён в параметрах реального тока по пространству, в то время как значение изменения напряжённости электрического поля
никак не может быть отражён в параметрах реального тока по пространству, в то время как значение изменения напряжённости электрического поля ![]() имеет конкретное представление в пространстве. С другой стороны, формальное математическое образование магнитного поля по формуле (50) с точки зрения наблюдаемого физического процесса необходимо представить через движение конкретного объекта в виде:
имеет конкретное представление в пространстве. С другой стороны, формальное математическое образование магнитного поля по формуле (50) с точки зрения наблюдаемого физического процесса необходимо представить через движение конкретного объекта в виде:
![]() , (57)
, (57)
Иными словами, представлять ток в виде стационарной величины неизменяемой во времени не корректно, так как он образуется за счёт движения зарядов, которые имеют электрическое поле и понятно, что движение зарядов вызывает и изменение во времени электрического поля в пространстве. В противном случае электрическое поле и заряд независимы друг от друга. При этом плотность заряда по теории Дирака [18, с. 349], может равняться только плюс или минус единице (![]() ), так как это значение не входит в саму формулу энергии Эйнштейна. Таким образом, если под изменением в пространстве при движении объекта (заряда) понимать изменение электрического поля (иное бы исключало взаимодействие через электрическое поле), то мы будем иметь:
), так как это значение не входит в саму формулу энергии Эйнштейна. Таким образом, если под изменением в пространстве при движении объекта (заряда) понимать изменение электрического поля (иное бы исключало взаимодействие через электрическое поле), то мы будем иметь:
![]() , (58)
, (58)
В этом случае уравнение (56) при учёте (55) должно иметь вид:
![]() , (59)
, (59)
Здесь значение знаков в правой части от знака равенства учитывает, что в противном случае мы приходим к противоречию, когда изменение во времени не приводит к изменению в пространстве, то есть к чудесам возникновения из нуля. При этом мы имеем совмещение реального тока со значением изменения реального электрического поля Е по координатам пространства, и наличие фиктивного тока смещения, выраженного через некую величину G, которая не имеет представления по пространственным координатам в силу того, что с учётом ортогональности (перпендикулярности) напряжённостей электрических и магнитных полей для величины G нет ортогональной координаты по пространству.
Однако, если убрать значение ![]() из формулы (59), то сразу натыкаемся на парадокс, при котором изменение во времени не приводит к изменению в пространстве в силу того, что ротор – это замкнутая величина при равенстве составляющих по координатам. Неравенство же приводит к уравнению непрерывности с переходом от замкнутого движения к прямолинейному. В этом случае мы бы не имели замкнутого движения по ротору и в законе Фарадея (49), что было отмечено нами выше.
из формулы (59), то сразу натыкаемся на парадокс, при котором изменение во времени не приводит к изменению в пространстве в силу того, что ротор – это замкнутая величина при равенстве составляющих по координатам. Неравенство же приводит к уравнению непрерывности с переходом от замкнутого движения к прямолинейному. В этом случае мы бы не имели замкнутого движения по ротору и в законе Фарадея (49), что было отмечено нами выше.
Таким образом, эти два закона по формулам (49) и (58) проверенные на практике противоречат третьему закону, также проверенному на практике, и это закон Умова – Пойтинга (аналог это уравнение непрерывности), по которому изменение по количеству во времени величины энергии соответствует её изменению по количеству в пространстве, и математически это выражается в виде формулы [19, с. 44]:
![]() , (60)
, (60)
Иное означало бы чудо возникновения из нуля и исчезновение в ноль. Отсюда имеем парадоксы, при которых обычные уравнения Максвелла (49) и (58) не соответствуют уравнению (60), так как изменение электромагнитных составляющих, а они однозначно связаны с энергией, не приводит к изменению в пространстве. Повторим, ротор – замкнутая величина, и не даёт изменения в пространстве. Таким образом, остаётся понять, что должен собой представлять член изменения по пространству, который необходим в уравнениях (49) и (58) для соблюдения закона сохранения количества, так как изменение по времени есть, но оно не сопровождается изменением по пространству. Повторим, что, это соответствует чуду возникновения из ничего и исчезновению в ноль в пространстве, что исключает необходимость самих законов физики. Поэтому, изменение по пространству в уравнении (59) можно получить, если сделать запись с учётом условия выражения длины через время (r=ct) по геометрии Минковского и считать, что значение G отображается в проекции на время G=Gt, согласно преобразованию проекции длины в проекцию времени, и наоборот, в соответствии с СТО и ОТО Эйнштейна в виде:
![]() , (61)
, (61)
В этом случае учитывается, что в четырёхмерном градиенте производная по времени (t) идёт со знаком, противоположным производным по длине (r) [20, с. 271], что соответствует (60) и подмечено Фейнманом. В итоге мы видим наличие, соответствия справа от знака равенства, изменения во времени, с изменением слева от знака равенства в пространстве, и при этом исключается парадокс возникновения и исчезновения в ноль. Так как обнуления в физике в отличие от математики через вычитание не существует, то дифференциалы в уравнении (61) подчиняются закономерностям в (1) для выполнения общего закона мироздания. В противном случае получались бы объекты независимые от нашего мироздания. Однако, что собой представляет член Gt в пространственно-временном представлении не было ясно. Если исключить этот член Gt из пространственно-временного представления, то он автоматически не может быть обнаружен и существовать в мироздании, а необходимость его следует из исключения парадокса, при котором изменение во времени неизбежно должно приводить к изменению в пространстве. Отсюда следует, что необходимость использования в обычных уравнениях Максвелла, наряду с электромагнитными составляющими, сторонних токов (токов смещения) связана с исключением чудес с возникновением из нуля и исчезновением в ноль, и так как токи смещения не наблюдаются в пространстве, то они должны быть представлены наличием проекции на время в соответствии с преобразованиями Лоренца – Минковского по СТО и ОТО Эйнштейна. Действительно, где есть изменение, то там всегда есть движение, а при этом всегда выполняются преобразования Лоренца – Минковского и, следовательно, есть проекция на время. Следует отметить, что и с точки зрения практики уравнение (50) также нельзя было считать полным, так как при отключении от катушки индуктивности прикладываемого электрического поля, в катушке (рис. 7) некоторое время продолжает течь ток, образование которого связано именно с магнитным полем.
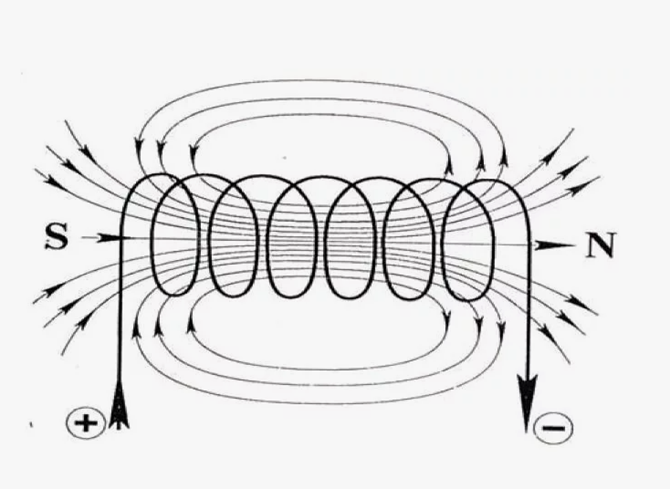
Рис. 7. Замкнутое поле катушки индуктивности в среде распространения, которое противодействует наличию тока в проводнике
Это означает, что состояние среды распространения (это характеризует среду распространения не как некий пустой вакуум равный нулю) изменилось под воздействием внешнего магнитного поля образуемого начальным током с наличием противодействия. Соответственно изменённое состояние среды распространения имеет количественную характеристику в виде энергии противодействия магнитному внешнему полю. После снятия внешнего напряжения на катушке, накопленное в пространстве противодействие, также в виде замкнутого магнитного поля, преобразуется в электрическое поле с изменением по пространству, так как иначе движения зарядов не получить. Это явление наличия магнитного поля замечено на практике в сверхпроводниках. Так как внешнего электрического поля с градиентом изменения при этом не наблюдается, то в этом случае градиент изменения по пространству происходит за счёт проекции электрической составляющей на время, с соблюдением закона сохранения количества по уравнению (60). В противном случае преобразование замкнутого магнитного поля по пространству сразу в проекцию электрической составляющей по пространству исключает необходимость обмена между противоположностями за счёт движения, и противоречит необходимости преобразования проекции длины на проекцию во времени, и наоборот, в соответствии с СТО и ОТО Эйнштейна. Соответственно для образования замкнутого магнитного поля требовалось бы наличие только электрического поля без использования корпускулярных свойств объектов, действие и противодействие имели бы идентичный путь. Кроме того, это означало бы получение замкнутости по трём ортогональным координатам пространства с нарушением необходимости зависимых и независимых составляющих от двух глобальных противоположностей, что противоречит логике [1, с. 6-42].
Собственно, к необходимости наличия члена с проекцией на время Gt пришли и физики, когда попытались перейти от уравнений Максвелла к формированию волновых процессов с вынужденным излучением. Это им удалось сделать через дополнительные функции – векторные потенциалы. По сути изменения (динамика) от этих дополнительных функций в одной противоположности выражает статику напряжённостей электрических и магнитных полей в другой противоположности. Это позволило исключить парадокс независимого распространения плоской волны в силу отсутствия источника возбуждения. Здесь замкнутые величины в динамике неких вспомогательных функций А и Ф стали представлять в виде величин (то есть, объектов) неизменных во времени и пространстве через напряжённости магнитного и электрического поля (это и есть отражение искривления (неоднородности) по времени и пространству).
Причём векторный потенциал А должен был удовлетворять условию ![]() (это и есть неизменность по пространству с представлением в виде замкнутой величины), что достигалось посредством следующего уравнения [21, с. 118]:
(это и есть неизменность по пространству с представлением в виде замкнутой величины), что достигалось посредством следующего уравнения [21, с. 118]:
![]() , (62)
, (62)
Понятно, что при определении дивергенции от замкнутой величины в виде ротора мы будем иметь ноль. И отсюда запись (62) выглядит парадоксальной, так как тогда и ![]() . Однако это противоречие разрешимо, если считать, что слева и справа от знака равенства рассматриваются противоположности, и замкнутость в одной противоположности соответствует разомкнутости в другой противоположности. По сути, величина магнитного поля В представляется объектом-константой от rotА. В этом случае мы имеем, при нормировке на величину В, формулу
. Однако это противоречие разрешимо, если считать, что слева и справа от знака равенства рассматриваются противоположности, и замкнутость в одной противоположности соответствует разомкнутости в другой противоположности. По сути, величина магнитного поля В представляется объектом-константой от rotА. В этом случае мы имеем, при нормировке на величину В, формулу ![]() , и она при условии равенства возможна только при наличии закономерностей по формуле мироздания (1) справа от знака равенства. Подстановка этого выражения в уравнение
, и она при условии равенства возможна только при наличии закономерностей по формуле мироздания (1) справа от знака равенства. Подстановка этого выражения в уравнение ![]() даёт уравнение:
даёт уравнение:
![]() , (63)
, (63)
Чтобы удовлетворить этому уравнению выражение в скобках приравнивалось к величине градиента потенциальной функции, что исключало замкнутость, то есть имеем уравнение:
![]() , (64)
, (64)
В этом случае векторный потенциал А характеризовал замкнутые процессы при изменении по пространству, а векторный потенциал Ф, наоборот, определял разомкнутые процессы по пространству. Иными словами, А и Ф характеризуют противоположности по пространству.
Для непосредственной связи векторных потенциалов мы учитываем известную формулу из электродинамики [22, с. 165]:
![]() , (65)
, (65)
При этом принимаем, что v=c, и тогда векторные потенциалы А и Ф связаны так же, как компоненты электрического и магнитного поля по уравнению Н=сЕ, и характеризуют именно электромагнитное поле, но в противоположности. В этом случае величина Е по формуле (64) характеризуется в одинаковом количественном представлении с учётом r=ct в виде:
![]() , (66)
, (66)
При нормировке (64) на Е, с учётом того, что величина Е отражает противодействие величине В через знак минус как противоположности, мы получаем, что для выполнения равенства необходимо использовать закономерности слева от знака равенства по формуле мироздания (1). То есть, в электродинамику ещё до нас физики ввели интуитивно закон для любых объектов мироздания, соответствующей формуле (1), так как иначе объект, автоматически, становился бы независим от нашего мироздания. По сути, выражение (64) отражает, что Е как замкнутая величина также не изменяется. Далее, исходя из Н=сЕ (а это закон связи противоположностей через скорость обмена, которая равна скорости света, так как в противном случае между Е и Н нет отличий, а значит мы имеем парадокс отсутствия противоположностей), мы при замене электромагнитных составляющих на уравнения вектор – потенциалов, что соответствует смене системы наблюдения на противоположную, имеем:
| (67) |
Соответственно для значений Е и Н не остаётся иного физического аналога кроме как времени и пространства (при наблюдении из противоположности), которые тоже связаны при условии соблюдения СТО (а это закон сохранения количества) по преобразованиям Минковского в виде r=ct. Учитывая, что векторное отображение не определяет ортогональности противоположностей, какими являются А и Ф, которые аналогичны Е и Н, мы должны уравнение (67) расписать по координатам, то есть представить в виде количественных значений по четырём составляющим двух глобальных противоположностей, например:
![]() , (68)
, (68)
Другими словами, мы получили фактически соответствие ротора и уравнения непрерывности на основе векторных потенциалов при подчинении общей формуле мироздания (1), для выполнения уравнения (68). Надо отметить, что проекцию векторного потенциала на время также впервые ввели не мы, а физики, в частности Фейнман [20, с. 271]. Однако он не понял, что при однозначной связи вектор – потенциалов с электромагнитными составляющими с целью исключения неоднозначности (чудес) должны существовать и проекции на время электромагнитных составляющих. Таким образом, мы исключили парадокс классических обычных уравнений Максвелла, так как имеем замкнутость (закон сохранения количества) по противоположностям. При этом учитываем, что для производной по величине х для вектора – потенциала Ф не остаётся иных компонент, кроме как проекции Ф на время, то есть Фt. Это аналогично тому, как это было сделано Фейнманом в [20, с. 271]. Здесь надо заметить, что электрические и магнитные составляющие однозначно связаны в законах Фарадея и Био – Савара с реальными объектами, а эти объекты подчиняются преобразованиям Лоренца – Минковского, с наличием проекции на время. Если бы электрические и магнитные составляющие не имели бы проекцию на время, то о связи реальных объектов с электромагнитными процессами можно было бы забыть из-за независимости, и в этом случае нет закона их связи. Наличие проекции на время – это единственный способ сохранения объектов в замкнутом виде, так как все оставшиеся величины по проекциям координат независимы и перпендикулярны, а вот время и проекции по координатам имеют связь через преобразования Лоренца – Минковского.
Соответственно, теперь можно рассмотреть и саму цель применения физиками векторных потенциалов для перехода к волновым уравнениям.
С этой целью выпишем известные уравнения из классической электродинамики с учётом как электрических, так и магнитных сторонних токов в виде [23, с. 34]:
| (69) |
В этом случае мы ничего не выдумываем, а равенство для сторонних зарядов и токов ![]() , используется в квантовой механике для соответствия сторонних токов и зарядов преобразованиям Лоренца-Минковского [24, с. 300] в виде:
, используется в квантовой механике для соответствия сторонних токов и зарядов преобразованиям Лоренца-Минковского [24, с. 300] в виде:
| (70) |
Собственно такой записью с учётом сторонних электрических и магнитных зарядов мы учли, что в среде распространения нет электрических зарядов, а электромагнитные составляющие волны имеют замкнутый характер с полной симметрией и преобразованием противоположностей друг в друга по замкнутому циклу. В этом случае вид уравнений для электрических и магнитных составляющих не может отличаться, так как в противном случае будет неравенство с нарушением закона сохранения количества. Это характеризует электрическую и магнитную индукцию как разомкнутые величины на основе сторонних зарядов, смысл которых мы покажем несколько ниже, аналогично тому, как это было для векторного потенциала Ф в противоположности. Далее мы учтём уравнение (63) с подстановкой и заменой напряжённости электрического поля на векторные потенциалы и получим:
| (71) |
Такое действие используется в математике при переходе к выражению с одним видом функции через подстановку, и как было показано выше, этот метод применил и Дирак.
По нашей теории любое изменение означает переход в противоположность со сменой системы наблюдения и с заменой сложения на вычитание, и наоборот. Для величины векторного потенциала ![]() противоположностью для перехода является векторный потенциал
противоположностью для перехода является векторный потенциал ![]() с условием выполнения количественного равенства. Собственно, это правило интуитивно ввели в электродинамику физики, и отсюда в классической электродинамике в противовес уравнению (64) в одной противоположности физики были вынуждены ввести калибровку Лоренца отражающие процессы в другой противоположности со сменой переменных дифференцирования из-за смены системы наблюдения в виде [25, с. 119]:
с условием выполнения количественного равенства. Собственно, это правило интуитивно ввели в электродинамику физики, и отсюда в классической электродинамике в противовес уравнению (64) в одной противоположности физики были вынуждены ввести калибровку Лоренца отражающие процессы в другой противоположности со сменой переменных дифференцирования из-за смены системы наблюдения в виде [25, с. 119]:
![]() , (72)
, (72)
В итоге, было получено волновое уравнение в зависимости от так называемой плотности заряда в классической электродинамике в виде:
![]() , (73)
, (73)
Если учесть связь между векторным потенциалом А и Ф по формуле (65) с учётом v=c (![]() ), то получим второе известное уравнение для векторного потенциала А в классической электродинамике в виде [25, с. 119]:
), то получим второе известное уравнение для векторного потенциала А в классической электродинамике в виде [25, с. 119]:
| (74) |
Таким образом, так как противоположности связаны через скорость света, сторонняя плотность заряда в одной противоположности формирует волновую составляющую ![]() , а в другой противоположности это рассматривается как формирование волновой составляющей
, а в другой противоположности это рассматривается как формирование волновой составляющей ![]() под влиянием сторонней плотности тока. В силу того, что существует закон сохранения заряда в соответствии с теорией Дирака (
под влиянием сторонней плотности тока. В силу того, что существует закон сохранения заряда в соответствии с теорией Дирака (![]() ) и значение заряда не входит в формулу энергии Эйнштейна, а значит и не может быть самостоятельной величиной воздействия из-за отсутствия энергии (количества), то изменение сторонних (фиктивных) плотности заряда и плотности тока связано только с подчинением преобразованиям Лоренца – Минковского (70), и другого способа их изменения не предвидится. Отсюда следует вывод, что по уравнениям (73) и (74) изменение сторонней плотности заряда и плотности тока связано с константами электрической и магнитной проницаемости, так как ничего другого в физике для описания среды распространения, как объекта мироздания с влиянием и взаимодействием (иначе это ноль), – нет. А это означает, что тогда именно константы электрической и магнитной проницаемости должны быть связаны с преобразованиями Лоренца-Минковского, и это мы покажем несколько ниже.
) и значение заряда не входит в формулу энергии Эйнштейна, а значит и не может быть самостоятельной величиной воздействия из-за отсутствия энергии (количества), то изменение сторонних (фиктивных) плотности заряда и плотности тока связано только с подчинением преобразованиям Лоренца – Минковского (70), и другого способа их изменения не предвидится. Отсюда следует вывод, что по уравнениям (73) и (74) изменение сторонней плотности заряда и плотности тока связано с константами электрической и магнитной проницаемости, так как ничего другого в физике для описания среды распространения, как объекта мироздания с влиянием и взаимодействием (иначе это ноль), – нет. А это означает, что тогда именно константы электрической и магнитной проницаемости должны быть связаны с преобразованиями Лоренца-Минковского, и это мы покажем несколько ниже.
Следует отметить, что уравнения (73) и (74) не имеют решения в волновом виде с точки зрения распространяющейся волны с источниками возбуждения, так как для решения в волновом виде уравнение частицы с массой покоя должно иметь вид (35) с решением в виде функции Луи де Бройля (34), где в правой и левой части уравнения присутствует функция ![]() . Однако решения уравнений (73) и (74) соответствуют варианту взаимодействия со средой распространения через константы электрической и магнитной проницаемости с очевидным результатом для векторного потенциала Ф в виде:
. Однако решения уравнений (73) и (74) соответствуют варианту взаимодействия со средой распространения через константы электрической и магнитной проницаемости с очевидным результатом для векторного потенциала Ф в виде:
![]() , (75)
, (75)
Для векторного потенциала ![]() имеем решение:
имеем решение:
![]() , (76)
, (76)
При этом необходимо помнить, что аргументы функций в силу закона сохранения количества между противоположностями должны подчиняться условию:
| (77) |
В этом случае мы имеем:
| (78) |
Иными словами, это означает, что в системе наблюдения от аргументов функций значения энергии и импульсов отличаются от энергии и импульсов в системе наблюдения после решения уравнений (73) и (74). Такая разница связана с иерархическим построением мироздания с исключением замкнутого цикла с обратным возвращением на тот же уровень и возможностью создания вечного двигателя.
В силу того, что аргумент волновых функций из-за условия выполнения формулы Луи де Бройля (44) равен нулю, то мы можем использовать умножение и правых частей от знака равенства в уравнениях (73) и (74) на соответствующие волновые функции, аналогично тому как это сделал Шредингер и Дирак в квантовой механике [10, с. 31]:
| (79) |
В результате мы имеем выражение единого объекта через две волновые составляющие Аэ и Фэ. При этом мы имеем противоположные системы наблюдения для векторных потенциалов со связью через скорость света, а это означает их ортогональность. Так как процессы в противоположностях симметричны, то такой вид волн действителен и для электромагнитных составляющих. Однако здесь необходимо учесть, что в данном случае был использован только один вид стороннего электрического заряда и соответственно напряжённость электрического поля волны в одной противоположности представляется напряжённостью магнитного поля волны в другой противоположности, что соответствует электромагнитному континууму с преобразованием друг в друга электрических и магнитных компонент. То есть Аэ и Фэ представляют одну и ту же составляющую от одного стороннего электрического заряда (плотности), но в противоположностях. В реальности для исключения парадокса отсутствия закона сохранения количества из-за несимметричных уравнений мы имеем взаимодействие сторонних электрических и магнитных зарядов (далее будет показано, что разница противоположных зарядов основана на преобразованиях Лоренца) с образованием электромагнитной волны, к чему также интуитивно пришли и физики в классической электродинамике. Поэтому, в силу того, что мы имеем и сторонний магнитный заряд (это следует из симметрии составляющих в электромагнитной волне), то для него тоже должны существовать магнитные векторные потенциалы в виде [26, с. 118]:
![]() , (80)
, (80)
Отсюда с учётом изменения в пространстве магнитной составляющей с учётом ![]() имеем волновые уравнения вида:
имеем волновые уравнения вида:
| (81) |
Это уравнения с учётом, введённого Шредингером и Дираком умножения справа от знака равенства на волновую функцию, имеет вид:
| (82) |
В результате получаем решения аналогичные по виду (34):
| (83) |
Иными словами, мы получаем, что константы электрических и магнитных проницаемостей меняются местами в зависимости от того, какая плотность стороннего заряда (электрическая или магнитная) рассматривается. Как мы отмечали выше, значение заряда по теории Дирака не может быть дробным и не входит в уравнение энергии Эйнштейна (![]() ), но наличие силы Лоренца и Кулона между так называемыми электрическими зарядами практически наблюдается, то отсюда следует вывод об иной природе образования этих сил, помимо возникновения их из неких зарядов, которые не имеют представления в параметрах окружающей среды, а значит, нет механизма взаимодействия. И собственно, само получение этих сил было представлено через СТО Эйнштейна на основе относительности электрических и магнитных полей, которые соответственно и являются источниками получения этих сил [27, с. 273].
), но наличие силы Лоренца и Кулона между так называемыми электрическими зарядами практически наблюдается, то отсюда следует вывод об иной природе образования этих сил, помимо возникновения их из неких зарядов, которые не имеют представления в параметрах окружающей среды, а значит, нет механизма взаимодействия. И собственно, само получение этих сил было представлено через СТО Эйнштейна на основе относительности электрических и магнитных полей, которые соответственно и являются источниками получения этих сил [27, с. 273].
Аналогичную интерпретацию ввёл, и Фейнман при описании относительности электрических и магнитных полей для плотности зарядов связав их законом действительным для преобразований Лоренца в виде:
| (84) |
Здесь v – относительная скорость по СТО Эйнштейна, ![]() – плотность заряда. Повторим, что в среде распространения мы движущихся электрических зарядов не наблюдаем, а значит, нет причины говорить об их плотности с подчинением СТО Эйнштейна. Тогда как обеспечивается противодействие току в магнитной катушке и зависимость наличия разной напряжённости электромагнитных полей в зависимости от направления? Иными словами, электрическим зарядам на основе электрона и позитрона в среде распространения должна быть замена с подчинением СТО и ОТО Эйнштейна. Если предположить объекты не связанные со средой распространения с характеристикой вне пространства и времени, то разные объекты должны иметь и отличие по подчинению законам физики, так как иначе не будет и самих различий. А раз различий в подчинении законам физики нет, то следует признать объекты идентичными. В этом случае с учётом начальной связи длины и времени (l=ct) [2, с. 225-226] и однозначной заменой сторонних зарядов, мы имеем уравнения:
– плотность заряда. Повторим, что в среде распространения мы движущихся электрических зарядов не наблюдаем, а значит, нет причины говорить об их плотности с подчинением СТО Эйнштейна. Тогда как обеспечивается противодействие току в магнитной катушке и зависимость наличия разной напряжённости электромагнитных полей в зависимости от направления? Иными словами, электрическим зарядам на основе электрона и позитрона в среде распространения должна быть замена с подчинением СТО и ОТО Эйнштейна. Если предположить объекты не связанные со средой распространения с характеристикой вне пространства и времени, то разные объекты должны иметь и отличие по подчинению законам физики, так как иначе не будет и самих различий. А раз различий в подчинении законам физики нет, то следует признать объекты идентичными. В этом случае с учётом начальной связи длины и времени (l=ct) [2, с. 225-226] и однозначной заменой сторонних зарядов, мы имеем уравнения:
| (85) |
Иными словами, мы представили сторонние плотности электрических и магнитных зарядов на то, что реально существует на практике при математическом описании, а это длина и время приведённые в одну систему наблюдения с учётом ОТО Эйнштейна, где v связано с кинетической энергией в противоположности. Именно представление противоположных зарядов по (85) в качестве объектов длины и времени, что также сделано до нас интуитивно Фейнманом, позволяет интерпретировать эти противоположные заряды как эквиваленты электрических и магнитных зарядов. То есть, это снимает проблему отсутствия магнитных зарядов, так как они уже учтены в качестве противоположных объектов в усовершенствованных уравнениях Максвелла, и из (85) видно, что различие противоположностей определяется не только знаком заряда, а ещё и зависимостью преобразования. Собственно отличие только на знак означало бы обнуление с отсутствием необходимости преобразования и взаимодействия. А в реальности мы имеем аннигиляцию позитрона и электрона (или протона и антипротона) с преобразованием в электромагнитные волны.
Так как плотности электрических и магнитных зарядов, согласно корпускулярно-волновому представлению любого объекта, отражаются в обеих противоположностях, то здесь с учётом зависимостей для векторных потенциалов, введённых в классической электродинамике [28, с. 39], аналогично законам электродинамики по уравнениям Максвелла, мы имеем образование напряжённостей электрических и магнитных полей в среде распространения как результат от сумм воздействия уравнений:
| (86) |
Иными словами, напряжённости полей в нашей системе наблюдения – это результат выполнения взаимодействия объектов по законам электродинамики в соответствии с уравнениями Максвелла в противоположной системе наблюдения, связанной с нашей через скорость света, через сложение и вычитание, но через противоположные компоненты по сравнению с теми которые были в первоначальном виде уравнений. Это, собственно, и означает новое взаимодействие. Соответственно изменения этих напряжённостей полей в пространстве приводят к формированию обмена электромагнитными волнами, как это было показано выше. При этом константы электрической и магнитной проницаемости должны выражаться через реальные объекты (иначе их вообще не может быть в уравнениях Максвелла). То есть, они также должны представляться в корпускулярно-волновом виде по функциям Луи де Бройля.
Собственно, исходя из вида функций Луи де Бройля, в данном случае константы электрической и магнитной проницаемости можно считать комплексными величинами, что также было введено в классическую электродинамику до нас [29, с. 117]. Действительно обычное уравнение Максвелла в частных производных представляется в виде:
![]() , (87)
, (87)
При представлении в электродинамике значения магнитной проницаемости в комплексном виде, что, кстати, позволяет решить проблему изменения направления движения по принципу Гюйгенса – Френеля в силу взаимодействия со средой распространения, имеем:
![]() , (88)
, (88)
Здесь i=(-1)1/2. При подстановке получаем:
![]() , (89)
, (89)
То есть классическая электродинамика при допущении наличия комплексных значений электрической и магнитной проницаемости потребовало и комплексный вид для уравнений Максвелла с наличием комплексных волновых электромагнитных функций аналогичных функциям Луи де Бройля. Будем считать, что здесь значение ![]() одинаковой величины в действительной и мнимой части, так как среда распространения не изменяет объект (например, фотон), движущийся со скоростью света, и сама не изменяется при взаимодействии. В противном случае объект исчезает в ноль или будет расти до бесконечности из нуля, в силу отсутствия закона сохранения количества. Иными словами, среда распространения, в данном случае, характеризует взаимодействие без изменений при сохранении в ней движущегося объекта, так как не может поглощать или синтезировать (в данном случае нет преобразования с возникновением новых объектов), что означало бы чудеса. То есть, мы при условии закона сохранения количества и неизменности среды распространения имеем:
одинаковой величины в действительной и мнимой части, так как среда распространения не изменяет объект (например, фотон), движущийся со скоростью света, и сама не изменяется при взаимодействии. В противном случае объект исчезает в ноль или будет расти до бесконечности из нуля, в силу отсутствия закона сохранения количества. Иными словами, среда распространения, в данном случае, характеризует взаимодействие без изменений при сохранении в ней движущегося объекта, так как не может поглощать или синтезировать (в данном случае нет преобразования с возникновением новых объектов), что означало бы чудеса. То есть, мы при условии закона сохранения количества и неизменности среды распространения имеем:
![]() , (90)
, (90)
Здесь мнимая единица i выступает как атрибут противоположности и фактически выражает закон, по которому на действие одной противоположности происходит противодействие, что и выражается возвратом со знаком минус при двойном изменении. Равенство действительной и мнимой части также не наша выдумка, и следует из вида уравнений в системе Дирака. Собственно, для векторных потенциалов приравнивание iФ=А4 [30, с. 317] к проекции на время At также было сделано в электродинамике Фейнманом [22, с. 165]. Однако хоть мы и придали мнимую единицу для различия в (89) с использованием комплексного значения магнитной проницаемости одной из составляющих ![]() , но путь изменения в зависимости от времени остался одинаковым. В этом случае составляющие могут только, одновременно, расти или убывать в силу одинаковых закономерностей и необходимости соблюдения равного количественного соотношения. Здесь нет взаимодействия через обмен, за счёт преобразования по противоположностям длины и времени в соответствии с СТО и ОТО Эйнштейна. Поэтому, не нарушая вида уравнения, мы умножаем числитель и знаменатель мнимой производной
, но путь изменения в зависимости от времени остался одинаковым. В этом случае составляющие могут только, одновременно, расти или убывать в силу одинаковых закономерностей и необходимости соблюдения равного количественного соотношения. Здесь нет взаимодействия через обмен, за счёт преобразования по противоположностям длины и времени в соответствии с СТО и ОТО Эйнштейна. Поэтому, не нарушая вида уравнения, мы умножаем числитель и знаменатель мнимой производной ![]() на скорость света:
на скорость света:
![]() , (91)
, (91)
С математической точки зрения при исходном уравнении (89) ничего не поменялось, а с физической точки зрения мнимая производная отражает противоположность, где за счёт скорости света проекции длины и времени меняются местами. Иначе при сохранении одинакового вида представления объектов при разнице в скорость света нет отличий, и это исключает наличие противоположностей. Отсюда и смена функций при переходе в противоположную систему наблюдения. При этом, на основе преобразований Лоренца – Минковского, проекция времени однозначно преобразовывается в проекцию длины, а проекция длины в проекцию времени в равных количествах в соответствии с СТО и ОТО Эйнштейна, аналогично и составляющие полей, что и было подмечено Фейнманом для векторных потенциалов. Ему оставалось лишь только признать наличие проекций на время для электромагнитных составляющих, что вытекало из однозначной связи векторных потенциалов с электромагнитными составляющими, но он этого не понял и посчитал, что это не так, о чём сказал в [22, с. 165]. Собственно, это заблуждение на самом деле связано с тем, что он исходил из отсутствия электромагнитного происхождения массы частиц, так как считал, что для этого необходимы дополнительные сдерживающие силы. Однако если считать функции в системе уравнений Дирака не вероятностными функциями, а электромагнитными функциями, то никаких сдерживающих сил при переходе от волнового вида к корпускулярному виду не требуется, так как нет дополнительных членов для выполнения равенств в системе уравнений Дирака.
Отметим также, что выражение процесса по Фарадею вида (87) не может отражать ни один реальный объект, так как нет зависимости процесса по координате z. В этом случае замкнутый обмен между противоположностями получить невозможно. То есть, в этом случае объект, характеризуемый через процесс (87), не будет связан с нашим мирозданием, а это элемент чуда. Отсюда с учётом z=ct и ![]() имеем:
имеем:
![]() , (92)
, (92)
Одновременно данный вид соответствует элементарному объекту мироздания, когда процесс в левой части уравнения (92) характеризует разомкнутость (замкнутость на противоположность по времени ![]() ), в силу невозможности наблюдать проекцию на время, а процесс, справа от знака равенства уравнения (92) характеризует замкнутость объекта. Таким образом, объект мироздания взаимодействует с другими объектами благодаря не наблюдаемому в пространстве члену
), в силу невозможности наблюдать проекцию на время, а процесс, справа от знака равенства уравнения (92) характеризует замкнутость объекта. Таким образом, объект мироздания взаимодействует с другими объектами благодаря не наблюдаемому в пространстве члену ![]() , и имеет необходимую замкнутость для своего отдельного существования, исходя из наличия операции ротора (rot). Надо отметить, что в противоположности замкнутость (rot) по координатам длины переходит в замкнутость по оставшейся координате длины и времени, и наоборот. Понятно, что меньше 4-х ортогональных составляющих в уравнении (92) при описании объектов мироздания иметь нельзя, так как приходим к парадоксу совпадения пути действия и противодействия. Отсутствие одинакового вида дифференциальных членов для магнитных и электрических составляющих говорит о представлении их как противоположностей. Одновременно вид уравнения (92) может быть выражен в базисном разложении в соответствии с общей формулой мироздания, так как в противном случае он оказывается независимым объектом, замкнутым сам на себя. Действительно в соответствии с [1, с. 6-42] при необходимом базисном разложении через функции (иначе закон мироздания (1) не получить), мы можем представить, что
, и имеет необходимую замкнутость для своего отдельного существования, исходя из наличия операции ротора (rot). Надо отметить, что в противоположности замкнутость (rot) по координатам длины переходит в замкнутость по оставшейся координате длины и времени, и наоборот. Понятно, что меньше 4-х ортогональных составляющих в уравнении (92) при описании объектов мироздания иметь нельзя, так как приходим к парадоксу совпадения пути действия и противодействия. Отсутствие одинакового вида дифференциальных членов для магнитных и электрических составляющих говорит о представлении их как противоположностей. Одновременно вид уравнения (92) может быть выражен в базисном разложении в соответствии с общей формулой мироздания, так как в противном случае он оказывается независимым объектом, замкнутым сам на себя. Действительно в соответствии с [1, с. 6-42] при необходимом базисном разложении через функции (иначе закон мироздания (1) не получить), мы можем представить, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . В результате вид уравнения (87) по закону Фарадея не может дать соответствие с формулой мироздания (1) при представлении через функции. Это значит, что по математической формуле (87) не отражается ни один реальный объект мироздания, так как не выполняется условие, при котором сложение в одной противоположности должно выражаться через вычитание в другой противоположности. В противном случае мироздание не замкнутая система с наличием чудес, а объекты без наличия замкнутости в принципе бы не существовали. Надо ещё раз отметить, что представление компонент дифференциального уравнения (92) через соотношения Эйлера были сделаны до нас. С этой целью в системе уравнений Дирака были использованы волновые функции Ψ, которые характеризовали вероятность. Кроме того, мы показали, что изначальная формула энергии Эйнштейна, из которой получается система уравнений Дирака также связана с формулой мироздания по формулам (22, 23, 24). Одновременно, если считать координаты длины и времени не подчиняющимися преобразованиям Лоренца – Минковского (гиперболические синус и косинус, с переходом в синус и косинус при смене системы наблюдения за счёт мнимой единицы), то получается система координат по геометрии Эвклида, что не соответствует замкнутой системе мироздания. Собственно иная интерпретация дифференциалов без представления через указанные закономерности не даст равенства при преобразовании и объект либо исчезнет, либо будет расти до бесконечности в одной из противоположностей. Иными словами уравнение (92), которое практически интуитивно было введено в электродинамику физиками, исходя из комплексных значений электрической и магнитной проницаемости, соответствует математическому равенству с подчинением уравнению энергии Эйнштейна (а из него и была выведена система уравнений Дирака), если при этом исключается линейность координат длины и времени по геометрии Эвклида. Таким образом, наши оппоненты пытаются опровергнуть то, что уже давно интуитивно было введено в электродинамику. Отличие в том, что мы показали логическую цепочку рассуждений, которые приводят к виду уравнений (92), с исключением иных представлений. Соответственно, мы получаем усовершенствованные уравнения Максвелла:
. В результате вид уравнения (87) по закону Фарадея не может дать соответствие с формулой мироздания (1) при представлении через функции. Это значит, что по математической формуле (87) не отражается ни один реальный объект мироздания, так как не выполняется условие, при котором сложение в одной противоположности должно выражаться через вычитание в другой противоположности. В противном случае мироздание не замкнутая система с наличием чудес, а объекты без наличия замкнутости в принципе бы не существовали. Надо ещё раз отметить, что представление компонент дифференциального уравнения (92) через соотношения Эйлера были сделаны до нас. С этой целью в системе уравнений Дирака были использованы волновые функции Ψ, которые характеризовали вероятность. Кроме того, мы показали, что изначальная формула энергии Эйнштейна, из которой получается система уравнений Дирака также связана с формулой мироздания по формулам (22, 23, 24). Одновременно, если считать координаты длины и времени не подчиняющимися преобразованиям Лоренца – Минковского (гиперболические синус и косинус, с переходом в синус и косинус при смене системы наблюдения за счёт мнимой единицы), то получается система координат по геометрии Эвклида, что не соответствует замкнутой системе мироздания. Собственно иная интерпретация дифференциалов без представления через указанные закономерности не даст равенства при преобразовании и объект либо исчезнет, либо будет расти до бесконечности в одной из противоположностей. Иными словами уравнение (92), которое практически интуитивно было введено в электродинамику физиками, исходя из комплексных значений электрической и магнитной проницаемости, соответствует математическому равенству с подчинением уравнению энергии Эйнштейна (а из него и была выведена система уравнений Дирака), если при этом исключается линейность координат длины и времени по геометрии Эвклида. Таким образом, наши оппоненты пытаются опровергнуть то, что уже давно интуитивно было введено в электродинамику. Отличие в том, что мы показали логическую цепочку рассуждений, которые приводят к виду уравнений (92), с исключением иных представлений. Соответственно, мы получаем усовершенствованные уравнения Максвелла:
| (93) |
Здесь ![]() . Существует также и комплексно-сопряжённая форма записи этих уравнений. Так как, полученные уравнения фактически отражают общую формулу мироздания (1), а это необходимое условие существования объекта в нашем мироздании (иначе он ноль), то величинами, определяющими параметры объекта, являются константы электрической и магнитной проницаемости. Так как у нас векторные потенциалы имеют аналогичные законы физики совпадающими с электромагнитными составляющими, но в противоположности, то отсюда имеем вид в частных производных для векторных потенциалов в виде:
. Существует также и комплексно-сопряжённая форма записи этих уравнений. Так как, полученные уравнения фактически отражают общую формулу мироздания (1), а это необходимое условие существования объекта в нашем мироздании (иначе он ноль), то величинами, определяющими параметры объекта, являются константы электрической и магнитной проницаемости. Так как у нас векторные потенциалы имеют аналогичные законы физики совпадающими с электромагнитными составляющими, но в противоположности, то отсюда имеем вид в частных производных для векторных потенциалов в виде:
![]() , (94)
, (94)
В результате при отражении напряжённостей электрических и магнитных полей мы должны откорректировать уравнения (86) в виде:
| (95) |
Здесь: ![]() . Мы видим, что полученный вид уравнений в частных производных уже соответствует виду некоторых уравнений из системы Дирака (31).
. Мы видим, что полученный вид уравнений в частных производных уже соответствует виду некоторых уравнений из системы Дирака (31).
Понятно, что мы должны показать, как внесение мнимой единицы в уравнения Максвелла повлияло на переход к волновому виду уравнений. С этой целью мы должны учесть, что дивергенция (градиент) от напряжённости электрического или магнитного поля, в среде распространения, связана с изменением оставшейся компоненты проекции на время, как это видно из (93). В этом случае система уравнений (69) представляется в виде:
| (96) |
Отсюда при переходе к волновому виду через подстановку переменных имеем:
| (97) |
Иными словами, мы за счёт мнимой единицы сменили систему наблюдения, но при этом переход к волновому уравнению остался прежним. Следует отметить, что в классической электродинамике для перехода к волновому виду от векторного потенциала А используется также математическое уравнение:
![]() , (98)
, (98)
На сколько это корректно можно увидеть, если расписать данное уравнение, например по напряжённости магнитного поля Н в частных производных, то имеем:
| (99) |
Соответственно имеем от первого оператора ротора:
| (100) |
От второго оператора ротора имеем общее выражение:
| (101) |
Аналогично, от первого и второго операторов имеем равенства: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
От третьего оператора ротора имеем вид:
| (102) |
Здесь от первого и третьего оператора следуют равенства: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
От второго и третьего операторов имеем: ![]() ,
, ![]() ,
, ![]() .
.
Соответственно мы видим, что члены с дифференцированием одновременно по двум ортогональным координатам по пространству имеют обнуление за счёт одинаковых членов из-за разницы знаков.
При этом, исходя из (98), мы должны иметь:
| (103) |
Однако и тут мы видим, что с математической точки зрения разница получаемых членов только в смене знака. Иное представление в виде ![]() и
и ![]() это только пожелания математиков для физики реальных процессов. При этом мы имеем ноль по математике, что в физике означает исчезновение в ноль, а это чудо, так как ни один объект мироздания не может выйти или войти в замкнутую систему Мироздания, поделённую на две глобальные противоположности. С отсутствием обнуления физики столкнулись при аннигиляции электрона и позитрона, когда разница знаков у зарядов дало не ноль, а фотоны с суммой энергий от электрона и позитрона. Кроме того, обнуления нет и при интерференции электромагнитных волн, так как вычитание электромагнитных волн не даёт обнуление, так как есть дальнейшее распространение волны, а это может происходить только при переходе взаимодействия по замкнутому циклу с преобразованиями между противоположностями. Соответственно с этим должно быть решение этого парадокса с исключением обнуления. Понятно, что, так как в физике нуля как такового нет, то это означает, изменение, связанное с ротором, должно противодействовать замкнутости по первому ротору, а это возможно только в том случае, когда мы имеем превращение единого замкнутого объекта в противоположное незамкнутое представление, при котором изменение в пространстве означает изменение по времени. Иными словами, первоначальный ротор по пространству должен преобразовываться в уравнение непрерывности (замкнутость по оставшейся проекции по координате длины и проекции по времени) или в подобное уравнение. В противном случае мы не имеем изменений с наличием преобразований, а значит, и нет самого воздействия. Однако в силу того, что мы имеем одинаковые компоненты по величине (это закон сохранения количества), то разница, исходя из наличия в мироздании противоположностей, может быть представлена в виде атрибута мнимой единицы (i=(-1)1/2). Исключить мнимую единицу при преобразовании (дифференцировании или интегрировании) мы не можем, так как в этом случае (как это было показано в [1, с. 6-42]), мы не будем иметь при переходе смену закономерностей, а значит и наличие самих противоположностей с их отличием друг от друга. Собственно, и здесь мы не первопроходцы, нечто подобное сделали физики в квантовой механике сделав приравнивание r=ict [30, с. 317] при рассмотрении дифференциальных компонент векторных потенциалов с представлением электромагнитного поля, вместо r=ct по геометрии Минковского [2, с. 225-226], которое отображает статику длины и времени по СТО и ОТО Эйнштейна через закономерности. Фактически это можно рассматривать как смену системы наблюдения со сменой динамики на статику и наоборот, где вычитание в одной противоположности одинаковых членов с обнулением, рассматривается в противоположности как наличие двух противоположных объектов. Иное бы исключало наличие противоположных систем наблюдения и понятно, что обнуление в обеих противоположностях не могло бы дать дальнейшего распространения волны при интерференции.
это только пожелания математиков для физики реальных процессов. При этом мы имеем ноль по математике, что в физике означает исчезновение в ноль, а это чудо, так как ни один объект мироздания не может выйти или войти в замкнутую систему Мироздания, поделённую на две глобальные противоположности. С отсутствием обнуления физики столкнулись при аннигиляции электрона и позитрона, когда разница знаков у зарядов дало не ноль, а фотоны с суммой энергий от электрона и позитрона. Кроме того, обнуления нет и при интерференции электромагнитных волн, так как вычитание электромагнитных волн не даёт обнуление, так как есть дальнейшее распространение волны, а это может происходить только при переходе взаимодействия по замкнутому циклу с преобразованиями между противоположностями. Соответственно с этим должно быть решение этого парадокса с исключением обнуления. Понятно, что, так как в физике нуля как такового нет, то это означает, изменение, связанное с ротором, должно противодействовать замкнутости по первому ротору, а это возможно только в том случае, когда мы имеем превращение единого замкнутого объекта в противоположное незамкнутое представление, при котором изменение в пространстве означает изменение по времени. Иными словами, первоначальный ротор по пространству должен преобразовываться в уравнение непрерывности (замкнутость по оставшейся проекции по координате длины и проекции по времени) или в подобное уравнение. В противном случае мы не имеем изменений с наличием преобразований, а значит, и нет самого воздействия. Однако в силу того, что мы имеем одинаковые компоненты по величине (это закон сохранения количества), то разница, исходя из наличия в мироздании противоположностей, может быть представлена в виде атрибута мнимой единицы (i=(-1)1/2). Исключить мнимую единицу при преобразовании (дифференцировании или интегрировании) мы не можем, так как в этом случае (как это было показано в [1, с. 6-42]), мы не будем иметь при переходе смену закономерностей, а значит и наличие самих противоположностей с их отличием друг от друга. Собственно, и здесь мы не первопроходцы, нечто подобное сделали физики в квантовой механике сделав приравнивание r=ict [30, с. 317] при рассмотрении дифференциальных компонент векторных потенциалов с представлением электромагнитного поля, вместо r=ct по геометрии Минковского [2, с. 225-226], которое отображает статику длины и времени по СТО и ОТО Эйнштейна через закономерности. Фактически это можно рассматривать как смену системы наблюдения со сменой динамики на статику и наоборот, где вычитание в одной противоположности одинаковых членов с обнулением, рассматривается в противоположности как наличие двух противоположных объектов. Иное бы исключало наличие противоположных систем наблюдения и понятно, что обнуление в обеих противоположностях не могло бы дать дальнейшего распространения волны при интерференции.
В итоге, исходя из практики наблюдаемых процессов, уравнение (98) с учётом преобразования F в иное представление за счёт изменения самих операций по взаимодействию в соответствующей системе наблюдения должно иметь вид:
![]() , (104)
, (104)
Иными словами, слева от знака равенства одна система наблюдения, которая равняется нулю, а справа от знака равенства противоположная система наблюдения с отсутствием обнуления. Как было показано нами в [31, с. 5-37], в этом случае с учётом калибровки Лоренца (72), мы имеем волновое уравнение в зависимости от тока смещения в виде:
| (105) |
Соответственно мы имеем преобразования электромагнитных составляющих в волновые уравнения в виде:
| (106) |
С переходом от сторонних зарядов на сторонние токи по (96) имеем:
| (107) |
Собственно, это означает, что волновые процессы в одной противоположности образуются за счёт сочетания, с взаимодействием через сложение и вычитание, замкнутого и разомкнутого движения в другой противоположности. Отметим, что, не надо думать, что это всё наши придумки, аналогичный вид был получен только в комплексном виде на основе векторных потенциалов и сторонних токов с взятием производной по времени в классической электродинамике [32, с. 40]:
| (108) |
Идентичность преобразований мы показали в [7, с. 9-45].
Теперь необходимо показать какие реальные объекты отражают усовершенствованные уравнения Максвелла. С этой целью вернёмся к системе уравнений Дирака (37), которая по мнению физиков служит для описания электронных и мюонных нейтрино (антинейтрино).
На основании логики при аннигиляции с учётом распада и превращении массы покоя в электромагнитные волны и с учётом того, что волновые свойства электромагнитной волны следуют из уравнений Максвелла, мы должны при преобразовании иметь изменения в системе (37). Так как для электромагнитной волны на основании использования обычных уравнений Максвелла используются две функции, отображающие напряжённости электрического и магнитного поля, то с учётом замены функций в системе (37) с трёх до двух, имеем независимые уравнения:
| (109) |
Суть преобразования в том, что, член производной по координате (у) в первом уравнении (37) в виде ![]() переставляется с членом производной из четвёртого уравнения
переставляется с членом производной из четвёртого уравнения ![]() . Аналогичная замена и в других уравнениях с учётом получения уравнения непрерывности в соответствии с усовершенствованными уравнениями Максвелла. При этом произошла смена знаков (иное бы противоречило наличию самих преобразований). Далее при преобразовании у нас значение
. Аналогичная замена и в других уравнениях с учётом получения уравнения непрерывности в соответствии с усовершенствованными уравнениями Максвелла. При этом произошла смена знаков (иное бы противоречило наличию самих преобразований). Далее при преобразовании у нас значение ![]() во втором уравнении замещает член
во втором уравнении замещает член ![]() в первом уравнении. Однако, с учётом перестановки, член
в первом уравнении. Однако, с учётом перестановки, член ![]() , переходит из первого уравнения во второе уравнение с наличием смены знака в виде
, переходит из первого уравнения во второе уравнение с наличием смены знака в виде ![]() . Суть смены знака при перестановке относительно Ψ3 связана с тем, что нейтрино и антинейтрино, которые отображаются в первом и втором уравнениях, должны иметь помимо представления в виде разомкнутой составляющей через уравнение непрерывности, и замкнутую составляющую в виде ротора. Иначе нет отображения распада в реальных объектах, и просто перестановка членов не даёт преобразований. Отсюда, с одной стороны, прямое замещение функций с перестановкой через Ψ4 от второго уравнения в первое уравнение. С другой стороны, при обратной перестановке Ψ3 из первого уравнения во второе уравнение, в системе (37), должно происходить со сменой знака через – Ψ3, что, собственно, отражает закон противодействия на действие, как это есть для взаимодействия по уравнениям Максвелла для электрических и магнитных компонент. Аналогичную перестановку по координате (z) мы имеем и для третьего и четвёртого уравнения. Это означает, что переход от свойств частицы к электронным и мюонным нейтрино (антинейтрино) связан не только с перестановкой и замещением членов в уравнениях с учётом закона сохранения количества, но и с изменением знака по одной из координат пространства. Собственно смена знака означает изменения в первоначальном взаимодействии, с отображением в ином виде за счёт смены закономерностей при соблюдении закона сохранения количества. Сокращение функций до двух (Ψ1 и Ψ2, или Ψ3 и Ψ4) означает отсутствие связи через массу покоя, а наличие двух функций в уравнении характеризует необходимость наличия в объекте противоположностей. Сократив на постоянную Планка ћ, (по математике этот коэффициент не влияет на результат) и умножив на (–i), что означает переход в противоположную систему наблюдения за счёт преобразования, мы получим:
. Суть смены знака при перестановке относительно Ψ3 связана с тем, что нейтрино и антинейтрино, которые отображаются в первом и втором уравнениях, должны иметь помимо представления в виде разомкнутой составляющей через уравнение непрерывности, и замкнутую составляющую в виде ротора. Иначе нет отображения распада в реальных объектах, и просто перестановка членов не даёт преобразований. Отсюда, с одной стороны, прямое замещение функций с перестановкой через Ψ4 от второго уравнения в первое уравнение. С другой стороны, при обратной перестановке Ψ3 из первого уравнения во второе уравнение, в системе (37), должно происходить со сменой знака через – Ψ3, что, собственно, отражает закон противодействия на действие, как это есть для взаимодействия по уравнениям Максвелла для электрических и магнитных компонент. Аналогичную перестановку по координате (z) мы имеем и для третьего и четвёртого уравнения. Это означает, что переход от свойств частицы к электронным и мюонным нейтрино (антинейтрино) связан не только с перестановкой и замещением членов в уравнениях с учётом закона сохранения количества, но и с изменением знака по одной из координат пространства. Собственно смена знака означает изменения в первоначальном взаимодействии, с отображением в ином виде за счёт смены закономерностей при соблюдении закона сохранения количества. Сокращение функций до двух (Ψ1 и Ψ2, или Ψ3 и Ψ4) означает отсутствие связи через массу покоя, а наличие двух функций в уравнении характеризует необходимость наличия в объекте противоположностей. Сократив на постоянную Планка ћ, (по математике этот коэффициент не влияет на результат) и умножив на (–i), что означает переход в противоположную систему наблюдения за счёт преобразования, мы получим:
| (110) |
Иными словами, мы имеем четыре независимых уравнения, причём первое и третье уравнения, а также второе и четвёртое уравнение идентичны по виду и отличаются только обозначениями через функции Ψ. При отсутствии взаимодействия их обнаружить в среде было бы невозможно. Именно поэтому, по мнению физиков, функции Луи де Бройля Ψ могут иметь скорость превышающую скорость света. В этом есть парадокс в системе уравнений Дирака, так как в силу отсутствия связи с окружающей средой изменения в функциях Ψ касаются лишь свойств движущейся частицы через аргументы от её энергии и импульсов по координатам. Для решения парадокса остаётся предположить, что функции Ψ должны быть связаны с электромагнитными функциями с учётом известных законов физики по электродинамике. В противном случае мы имеем разрыв в преобразованиях, а это равносильно чуду. Следовательно, если исходить из усовершенствованных уравнений Максвелла (93), то для получения идентичности с (110) для первого и третьего уравнений мы можем выразить функции Ψ следующим образом:
| (111) |
Иными словами, мы получаем физические аналоги реализаций функций Ψ1 и Ψ4, а также Ψ3 и Ψ2, выраженных через реальные электромагнитные составляющие по (93) с учётом констант электрической и магнитной проницаемости, то есть состояния среды. Это означает, что усовершенствованные уравнения Максвелла отражают реальные объекты в виде электронных и мюонных нейтрино и антинейтрино.
Соответственно, так как виды уравнений для электромагнитных составляющих и векторных потенциалов совпадают, то в обеих противоположностях мы имеем выражение в виде электронных и мюонных нейтрино (антинейтрино) в одном случае через электромагнитные составляющие, а в другом случае через векторные потенциалы. В противном варианте при нарушении симметрии представления мы бы не имели закон сохранения количества, то есть пришли бы к чудесам. Таким образом мы получили, что электронные и мюонные нейтрино (антинейтрино) определяются на основе усовершенствования уравнений Максвелла, а волновые электромагнитные процессы связаны с изменениями этих электронных и мюонных нейтрино при взаимодействии с учётом параметров среды распространения. Для окончательного получения логического смысла усовершенствованных уравнений Максвелла осталось выразить константы электрической и магнитной проницаемости с подчинением общей формуле мироздания (1) с учётом преобразований Лоренца – Минковского, так как никаких иных зависимостей в пространстве и времени не наблюдается.
С этой целью мы попытаемся объяснить необходимость первоначальной формулы, используемой в электродинамике по связи магнитных и электрических полей вида [16, с. 46]:
| (112) |
Здесь ![]() и
и ![]() константы магнитной и электрической проницаемости окружающей среды. При этом, в классической электродинамике в системе измерения СИ используется формула для вычисления волнового сопротивления среды в виде [33, с. 299]:
константы магнитной и электрической проницаемости окружающей среды. При этом, в классической электродинамике в системе измерения СИ используется формула для вычисления волнового сопротивления среды в виде [33, с. 299]:
![]() , (113)
, (113)
Следует отметить, что для системы измерения СГС (![]() ) вообще нет отличий между Е и Н в окружающей среде (вакууме) и таким образом вакуум соответствует геометрии Эвклида. В системе СИ электрическая (Е) и магнитная (Н) составляющая волны в среде распространения отличаются друг от друга только количественно, и не являются противоположностями, как, например, длина и время, которые связаны по теории Минковского [2, с. 225-226] через скорость света (r=ct). Но, если отличия только количественные, то это означает, что и законы физики должны быть одинаковые, чего на практике не наблюдается, так как нет никаких магнитных зарядов в пространстве, которые физики безуспешно ищут. Кроме того, отсутствие отличий между электрическими и магнитными составляющими исключает и взаимодействие, что соответствует противоположностям, так как для величин, отличающихся только количественно происходит ассоциативное сложение или вычитание (принцип суперпозиции). Это означает парадокс, и отсюда следует, что должна быть иная интерпретация констант электрической и магнитной проницаемости, при которой мы имели представление электрических и магнитных составляющих как противоположностей.
) вообще нет отличий между Е и Н в окружающей среде (вакууме) и таким образом вакуум соответствует геометрии Эвклида. В системе СИ электрическая (Е) и магнитная (Н) составляющая волны в среде распространения отличаются друг от друга только количественно, и не являются противоположностями, как, например, длина и время, которые связаны по теории Минковского [2, с. 225-226] через скорость света (r=ct). Но, если отличия только количественные, то это означает, что и законы физики должны быть одинаковые, чего на практике не наблюдается, так как нет никаких магнитных зарядов в пространстве, которые физики безуспешно ищут. Кроме того, отсутствие отличий между электрическими и магнитными составляющими исключает и взаимодействие, что соответствует противоположностям, так как для величин, отличающихся только количественно происходит ассоциативное сложение или вычитание (принцип суперпозиции). Это означает парадокс, и отсюда следует, что должна быть иная интерпретация констант электрической и магнитной проницаемости, при которой мы имели представление электрических и магнитных составляющих как противоположностей.
Выше мы показали, что электрическая и магнитная проницаемости, единственные параметры среды распространения, и с учётом того, что изменение значений сторонних токов и зарядов должно подчиняться преобразованиям Лоренца – Минковского, для выполнения закона сохранения количества, то отсюда константы электрической и магнитной проницаемости должны отражаться также через преобразования Лоренца -Минковского в соответствии с ОТО Эйнштейна. Иными словами, движение в противоположности, выраженное через кинетическую энергию, в нашей системе наблюдения представляется через пространственно-временное искривление (потенциальную энергию) с отображением через константы электрической и магнитной проницаемости, так как системы наблюдения отличаются на скорость света и покой в одной означает движение в другой.
Собственно иное представление исключало бы связь этих констант с нашим Мирозданием.
Отсюда имеем формулы для констант магнитной и электрической проницаемости в виде:
| (114) |
Так как, в силу симметрии противоположностей при законе сохранения количества, законы в противоположностях также аналогичны (иное даёт неравенство и исчезновение одной из противоположностей), то в силу того, что никем не придумано описания пространства и времени иначе, чем через пространственно-временное искривление, следует признать, что константы электрической и магнитной проницаемости связаны со скоростью (![]() ) в соответствии с ОТО Эйнштейна и вид этих констант должен иметь разное представление (иное опять приводит к однородности). То есть, в этом случае константы электрической и магнитной проницаемости не имеют подобный вид, а это даёт их представление как противоположностей, и при этом они отличаются на значение с2. Понятно, что наличие констант электрической и магнитной проницаемости в окружающей среде должно определять и соответствующие параметры частиц в Мироздании, так как взаимодействие частиц происходит именно через параметры окружающей среды. Однако так как нет зависимости констант электрической и магнитной проницаемости в среде распространения от конкретных частиц, то следует предположить, что при определении величин констант электрической и магнитной проницаемости мы должны опираться на общий закон взаимодействия противоположностей, который характеризует обменный процесс между противоположностями. Выше мы показали, что в среде распространения под воздействием констант электрической и магнитной проницаемости происходит формирование волновых процессов электромагнитного излучения. При этом в квантовой механике было показано, что между поглощением и излучением в среде распространения существует термодинамическое равновесие с получением формулы Планка для замкнутой системы, с исключением варианта «ультрафиолетовой катастрофы», и использованием закона Больцмана вида [34, с. 28]:
) в соответствии с ОТО Эйнштейна и вид этих констант должен иметь разное представление (иное опять приводит к однородности). То есть, в этом случае константы электрической и магнитной проницаемости не имеют подобный вид, а это даёт их представление как противоположностей, и при этом они отличаются на значение с2. Понятно, что наличие констант электрической и магнитной проницаемости в окружающей среде должно определять и соответствующие параметры частиц в Мироздании, так как взаимодействие частиц происходит именно через параметры окружающей среды. Однако так как нет зависимости констант электрической и магнитной проницаемости в среде распространения от конкретных частиц, то следует предположить, что при определении величин констант электрической и магнитной проницаемости мы должны опираться на общий закон взаимодействия противоположностей, который характеризует обменный процесс между противоположностями. Выше мы показали, что в среде распространения под воздействием констант электрической и магнитной проницаемости происходит формирование волновых процессов электромагнитного излучения. При этом в квантовой механике было показано, что между поглощением и излучением в среде распространения существует термодинамическое равновесие с получением формулы Планка для замкнутой системы, с исключением варианта «ультрафиолетовой катастрофы», и использованием закона Больцмана вида [34, с. 28]:
![]() , (115)
, (115)
По сути, это детерминированный закон связи между распадом в одной противоположности, и синтезом в другой противоположности, по замкнутому циклу обмена, причём без наличия вероятностей испускания и поглощения. В итоге нам следует выразить константы магнитной и электрической проницаемости через усреднённое (интегральное) движение частиц, со скоростью (кинетической энергией) в противоположной системе наблюдения ![]() , связанной с нашей системой наблюдения через скорость света. Усреднённое интегральное значение кинетической энергии от противоположности говорит о том, что любая частица в одной противоположности связана с взаимодействием и всеми частицами в другой противоположности через среду распространения. Понятно, что в этом случае среда распространения должна характеризовать и сами частицы взаимодействия исходя из обмена. В этом случае устойчивый обмен между частицами без распада мы получаем с учётом максимума энергии излучения по формуле Планка при коэффициенте 4,965 [35, с. 31]. Соответственно в силу того, что кинетическая энергия в одной противоположности представляется потенциальной энергией в другой противоположности, и наоборот, то противоположные частицы имеют отношение в разнице массы, исходя из констант электрической и магнитной проницаемости в соответствии с (114) и волнового сопротивления. Здесь мы учитываем, что в отличие от системы СИ по формуле (113) у нас отношение
, связанной с нашей системой наблюдения через скорость света. Усреднённое интегральное значение кинетической энергии от противоположности говорит о том, что любая частица в одной противоположности связана с взаимодействием и всеми частицами в другой противоположности через среду распространения. Понятно, что в этом случае среда распространения должна характеризовать и сами частицы взаимодействия исходя из обмена. В этом случае устойчивый обмен между частицами без распада мы получаем с учётом максимума энергии излучения по формуле Планка при коэффициенте 4,965 [35, с. 31]. Соответственно в силу того, что кинетическая энергия в одной противоположности представляется потенциальной энергией в другой противоположности, и наоборот, то противоположные частицы имеют отношение в разнице массы, исходя из констант электрической и магнитной проницаемости в соответствии с (114) и волнового сопротивления. Здесь мы учитываем, что в отличие от системы СИ по формуле (113) у нас отношение ![]() , а не просто число
, а не просто число ![]() [33, с. 299]. В итоге выше была получена формула отношения масс протона и электрона:
[33, с. 299]. В итоге выше была получена формула отношения масс протона и электрона:
![]() , (116)
, (116)
Некоторое небольшое отличие от практики (1836,1) в числовом значении есть, и оно связано с тем, что наши расчёты выполнены для более общего случая с делением только на протон и электрон. Кроме того, при динамике обмена обязательно должна быть энергия с соответствующей массой для излучения. Таким образом наша теория позволяет определить и разницу масс между протоном и электроном на основе СТО и ОТО Эйнштейна.
Следовательно, мы видим, что при определении законов физики за счёт элементарной логики на основе общей формулы мироздания (1), мы получили объяснение электронным и мюонным нейтрино (антинейтрино) и их преобразованию в электромагнитные волны. Отсюда следуют выводы:
- Из общего закона мироздания формируются практические уравнения для энергии Эйнштейна, а также преобразования Лоренца – Минковского с получением пространственно-временного искривления.
- Ошибка с попыткой обосновать наличие эфира и «эфирного ветра» связана с тем, что пространственно-временное искривление рассматривалось не как взаимодействие объектов мироздания путём обмена со скоростью света. При этом сами объекты для обмена представлялись виртуальными фотонами и гравитонами, которые вероятностно возникают и исчезают в так называемом вакууме.
- Хотя Дирак и использовал для получения своей системы уравнений с переходом от волновых свойств к корпускулярным детерминированное уравнение энергии Эйнштейна, но в качестве волновой функции он использовал функцию Луи де Бройля, которая по мнению физиков должна была отражать вероятностные свойства и иметь распространение с фазовой скоростью, превышающей скорость света. Это эквивалентно чудесам.
- Система уравнений Дирака не имела связи с окружающей средой распространения на основе констант электрической и магнитной проницаемости и поэтому не могла описать аннигиляцию электрона с позитроном с превращением в фотоны, волновые свойства которых следовали из уравнений Максвелла.
- Сами обычные уравнения Максвелла также не могли описывать корпускулярные свойства и тем самым отрицали необходимость корпускулярно-волнового дуализма.
- В соответствии с задачей исключения указанных парадоксов было показано, каким образом на основе логики надо усовершенствовать уравнения Максвелла, чтобы привести их к виду соответствующему электронным и мюонным нейтрино (антинейтрино) и обеспечить получение электромагнитной волны.
- Векторные потенциалы и электромагнитные составляющие в силу симметричности отражают одни и те же законы физики, но в противоположностях и динамика взаимодействия одних составляющих в одной противоположности рассматривается как статика корпускулярных свойств в другой противоположности.
- Константы электрической и магнитной проницаемости с учётом нашей теории приобретают логику соответствия общей формуле мироздания и законам физики с учётом преобразований Лоренца-Минковского.
- На основании нового вида представления констант электрической и магнитной проницаемости с учётом величины пика излучения по уравнению Планка удаётся вычислить значение отношения масс протона к массе электрона без использования неких кварков и глюонов.
- Условие относительности представления электрических и магнитных полей от системы наблюдения (электромагнитный континуум), с зависимостью плотности противоположных зарядов от подчинения преобразованиям Лоренца, определяет представление противоположных зарядов как объектов длины и времени. В среде распространения это выражается через константы электрической и магнитной проницаемости (они и отражают эти самые объекты длины и времени), так как сами заряды не входят в уравнение энергии Эйнштейна, а значит не могут обладать воздействием.
Следует отметить, что все использованные методы преобразования и уравнений давно известны в классической электродинамике, требовалось лишь показать логику данных преобразований и уравнений с исключением объяснений через чудеса (например, проникновения через потенциальный барьер – телепортацию). Полученная логика позволила также объяснить с научной точки зрения разницу масс между протоном и электроном без наличия кварков и глюонов, а также объяснила переход от электронных и мюонных нейтрино (антинейтрино) к электромагнитным волнам. Кроме того, было получено научное объяснение происхождения констант электрической и магнитной проницаемости. Это составляет несомненную научную ценность данной предлагаемой теории и статьи.
.png&w=384&q=75)
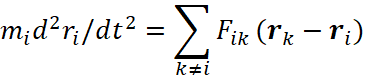
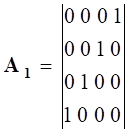
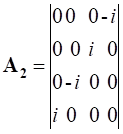
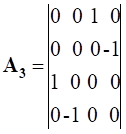
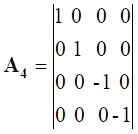 ,
,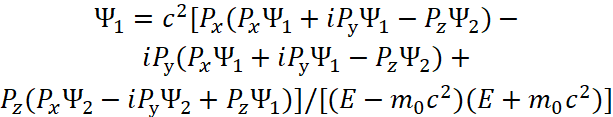 ;
;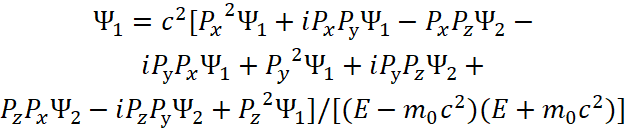 ,
,.png&w=640&q=75)