Образование в вузе должно соответствовать требованиям ФГОС ВО, концепции развития математического образования, запросам общества, нуждающегося в специалистах способных действовать в условиях неопределенности, многозадачности и быстро адаптироваться к изменяющимся условиям действительности. Вузы страны должны постоянно улучшать качество, уровень образовательной деятельности при обучении дисциплине «Высшая математика», чтобы каждое занятие способствовало развитию познавательного интереса к обучаемой дисциплине. Одним из путей решения данного вопроса при обучении дисциплины «Высшая математика» является включение в содержание курса данной дисциплины кейсов профессионально - ориентированных и прикладных задач. Которые обеспечат повышение уровня математической культуры будущих инженеров определяющие потенциал и значимость дисциплины «Математика», а также помогут применять полученные знания при решении профессиональных задач в будущей трудовой деятельности.
Значимую и главную роль в обучении дисциплины «Высшая математика» играют задачи. Большая часть учебного времени, объяснение теоретического материала, демонстрация примеров, при обучении данной дисциплине отводится на решение задач. Решение математических задач – является достижением целей обучения дисциплины «Высшая математика», развивается познавательная активность, интерес, обучающиеся приобретают новые знания, восполняются дефициты знаний по определенным темам, знакомятся с новыми методами решения задач, формируются исследовательские умения и навыки и применение математических знаний в будущей профессиональной деятельности и в повседневной жизни.
Роль изучения математических моделей играет большую роль в системе научных знаний, что позволяет обучающимся изучая сложные явления и процессы моделировать их и тем самым упрощать и изучать только некоторые их аспекты. А также изучая различные методы исследования этих моделей актуально в подготовке специалистов инженерно-технических специальностей для решения профессионально-ориентированных задач.
Освоения метода моделирования необходимо предоставить ученикам возможность самостоятельно строить модели и применять их для изучения различных объектов и явлений. И такие возможности есть рамках курсов математики [1].
Математическая модель – примерная модель объектов, явлений и процессов, показанной мате математическими символами и обозначениями, обусловленной на точном логическом мышлении [2].
По мнению автора Михайлова Д. Д. математическая модель системы или механизма есть совокупность математических объектов (чисел, переменных, множеств и т. д.) и зависимостей между ними, которая адекватно описывает свойства технического объекта. С их помощью возможно описывать характеристики и оценивать возможности конкретных систем и конструкций Математическое моделирование, в свою очередь, представлено в двух основных направлениях:
- построение моделей на основе прямой аналогии;
- построение моделей на основе компьютерного моделирования [3].
Автор Вакджира М. Б. определяет математическое моделирование, как методологию познания окружающей нас действительности, когда изучаемый процесс (объект, явление) заменяется его математической моделью – замкнутой системой уравнений, начальных, граничных и иных условий, которая представляет его свойства в виде определяющих соотношений, и требуемых характеристические функции процесса, которые находятся математическими методами [4].
- Математические модели являются наиболее общими и абстрактными. Для решения задачи при помощи математической модели необходимо следовать алгоритму:
- перейти от условия задачи к её математической модели;
- решить по заданному/определенному алгоритму модель;
- вернуться от математической модели к исходным условиям/реальной ситуации в задаче.
При решении практико-ориентированных, прикладных задач, построение математической модели является одним из сложных этапов работы, который в дальнейшем позволяет понять и позволить решить правильно данную задачу обучающимся.
Сложность составления математической модели заключается в том, что необходим определенный уровень знаний, умений по дисциплине «Математика», а также способность ориентироваться и применять данные знания.
Зачастую при решении математических задач, математическая модель представляет собой уравнения, систему линейных уравнений, где есть неизвестные, и есть данные позволяющие найти неизвестные переменные.
Уравнение – это аналог ситуации, когда объект неизвестен, но кое-что про него мы знаем.
Система уравнений – математическая модель задач линейного программирования, решения которых предполагает использование знаний и умений обращения с матричными моделями.
В связи с этим оправдано изучение раздела «Элементы линейной алгебры» в курсе дисциплины «Математика» для будущих инженеров.
Приведем примеры задач и их решения с использованием математического моделирования.
Пример 1
Пусть предприятие выпускает продукцию трёх видов 1 2 3, P P P, используя при этом три типа сырья 1 2 3 , , S S S . Нормы расхода сырья на единицу и расход сырья на один день представлены в Таблице 1. Требуется:
a) составить экономико-математическую модель ежедневного выпуска продукции каждого из трёх видов 1 2 3 , , PP P, предполагая полное использование сырья;
b) найти ежедневный объём выпуска каждого вида изделий (систему решить матричным методом).
Таблица 1
Нормы расхода сырья на единицу и расход сырья на один день
Тип сырья | Расход сырья на 1 день, усл. ед | Нормы расхода сырья на единицу продукции, усл. ед. | ||
|
| P1 | P2 | P3 |
S1 | 8900 | 7 | 4 | 2 |
S2 | 4550 | 2 | 3 | 2 |
S3 | 2350 | 0 | 1 | 5 |
Обозначим через ежедневный объём выпуска изделий вида P1, P2, P3 ответственно.
Составим математическую модель задачи.
| (1) |
![]() , (2)
, (2)
Система линейныйх уравнений (1) с ограничениями (2) представляет собой экономико-математическую модель ежедневного выпуска продукции вида P1, P2, P3.
Решив систему (1), найдем ежедневный объем выпуска продукции каждого вида в предположении полного использования сырья.
Перепишем систему (1) в матричном виде.
Матрица системы (1):
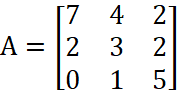 .
.
Матрица-столбец неизвестных:
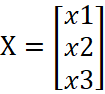 .
.
Матрица-столбец свободных членов:
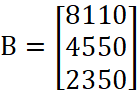 .
.
Тогда система (1) в матричном виде: AX = B.
Матрицу Х можно выразить, если умножить обе части этого уравнения слева на матрицу, обратную матрице А:
A -1 AB = A-1 B X = A-1B
Это уравнение можно решить, если определитель матрицы А не равен нулю:
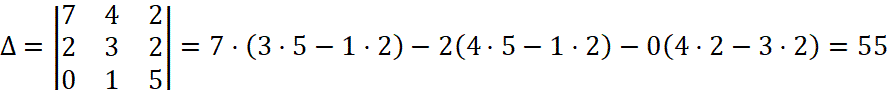 (не равно 0).
(не равно 0).
Обратная матрица будет иметь следующий вид:
 ,
,
Где Aij – алгебраические дополнения.
Транспонированная матрица имеет вид:
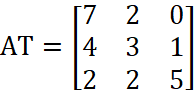 .
.
Найдем алгебраические дополнения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Обратная матрица равна:
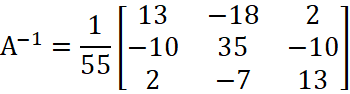 .
.
Так как, X = A-1B значения неизвестных равны:
| (3) |
Таким образом, ![]() ,
, ![]() ,
, ![]() , т. е. ежедневный объем выпуска продукции вида P1 составляет 700 ед., продукции вида P2 составляет 850 ед., продукции вида P3 – 300 ед.
, т. е. ежедневный объем выпуска продукции вида P1 составляет 700 ед., продукции вида P2 составляет 850 ед., продукции вида P3 – 300 ед.
Пример 2
Таблица 2
Ресурсы | Железнодорожная промышленность | Здравоохранение |
Электроэнергия | 10,2 | 6,1 |
Железнодорожные ресурсы | 7,2 | 3,5 |
Водные ресурсы | 4 | 1,2 |
Упрощённая запись предложенных аналитических данных выглядит следующим образом:
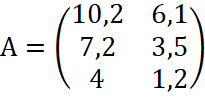 .
.
Решение экономических задач, осуществляемое матричным методом, позволило решать основные за дачи экономического профиля на любом из предприятий.
Пусть предприятие выпускает продукцию трёх видов (P1, P2, P3), использует сырьё двух типов (S1, S2), а нормы расхода:
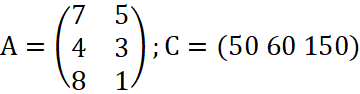 .
.
Стоимость единицы каждого типа сырья (ден. ед) представлена матрицей-столбцом: ![]() .
.
Решая данную задачу аналитически, получаем: – затраты 1-го сырья составляют S1 = 7 ⋅ 50 + 4 ⋅ 60 + 8 ⋅ 150 =1790 (ед.);– затраты 2-го сырья составляют S2 = 5 ⋅ 50 + 3 ⋅ 60 + 1 ⋅ 150 = 580 (ед.); поэтому матрица-строка затрат сырья S может быть записана как произведение: S=CA, где S – затраты сырья; С – заказ; A – матрица производства.
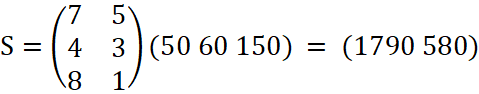 .
.
Общая стоимость сырья Q = 1790⋅50 + 580 ⋅ 45 = 115600 (ден. ед.) может быть записана в матричном виде: Q = SB = (CA)B = 115600, где Q – общая стоимость; B – стоимость единицы сырья; S – затраты сырья.
Применение матриц в экономике не может обойтись и без матрицы Абеля, т. к. она позволяет рассматриваемую отрасль какой-либо деятельности компании, привести к критериям выбора конкурентоспособности в технологиях синергетического эффекта и маркетинга.
Например, поступление товаров на первый склад описывается матрицей:
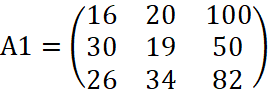 .
.
А поступление товаров на второй склад описывается матрицей:
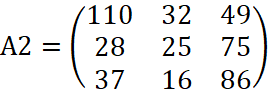 .
.
Найдите суммарный завоз товаров на склады; годовой завоз на склады, если по договору, производится ежемесячный завоз одинаковых партий товаров.
Решение:
Найдём суммарный завоз:
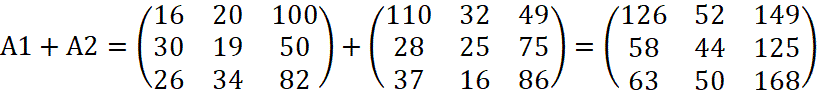 .
.
Найдём годовой завоз:
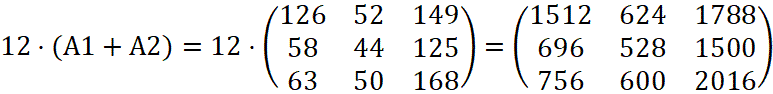 .
.
Ответ:
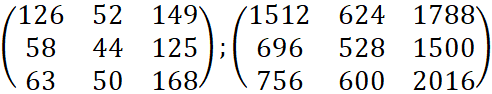 .
.
Использование метода математического моделирования при изучении дисциплин «Математика» позволяют обучающимся применять полученные знания в профессионально-ориентированных и прикладных задачах, повышает познавательную активность обучающихся.
.png&w=384&q=75)
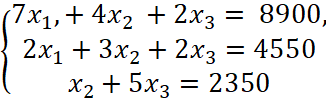
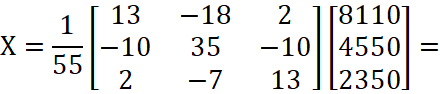
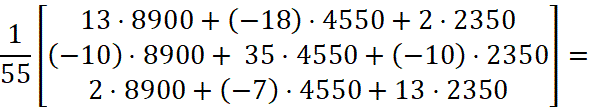
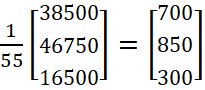 .
..png&w=640&q=75)