В статье [1, с. 6-42] мы показали, как на основе элементарной логики формируются законы Мироздания. Далее в статье [2, с. 29-63] мы связали эти законы с известными практическими законами физики, и, в частности, был приведён переход от электронных и мюонных нейтрино и антинейтрино к описанию волновых свойств объектов. Причём было показано, что математическое описание (на основе законов Мироздания) электронных и мюонных нейтрино (антинейтрино) соответствует классическим уравнениям электродинамики с учётом комплексных значений электрической и магнитной проницаемости и наличием проекций напряжённостей электрических и магнитных полей на время. Это обеспечивает подчинение электронных и мюонных нейтрино (антинейтрино) преобразованиям Лоренца – Минковского в соответствии с СТО и ОТО Эйнштейна. Более того, так как противоположности связаны через скорость света и представление о движении определяется от того в какой системе и в какой противоположности находится наблюдатель, было установлено, что значения констант электрической и магнитной проницаемости отражают кинетическую энергию (выраженную через скорость движения объектов) в противоположной системе наблюдения, в соответствии с ОТО Эйнштейна. И это отражается в нашей системе наблюдения через пространственно-временное искривление по ОТО Эйнштейна. Такая интерпретация позволила обосновать разницу масс между протоном и электроном. Однако теперь перед нами стоит задача математического описания синтеза корпускулярных свойств объектов. При этом получаемые уравнения должны соответствовать наблюдаемому практическому распаду масс по [3, с. 277] в виде:
| (1) |
Из (1) видно, что все распады на практике осуществляются через электронные и мюонные нейтрино (антинейтрино) ![]() с аннигиляцией частиц с превращением в фотоны
с аннигиляцией частиц с превращением в фотоны ![]() . При этом нет ни одного распада на гипотетические гравитоны, кварки, глюоны и виртуальные фотоны. Собственно, это подтверждает идею М. В. Ломоносова, что объект состоит из того, на что он распадается. Физики в своём желании выдачи желаемого за действительное даже не смогли сообразить, что если при аннигиляции электрона и позитрона (а они имеют массу покоя и тем самым должны взаимодействовать через гравитоны) образуются только фотоны, то места для гравитонов нет, как нет и самого способа преобразования гравитонов в электромагнитные волны. Иными словами природа гравитации также должна иметь описание через электромагнитное взаимодействие. Исходя из наблюдаемого практического распада частиц по (1), можно сделать вывод, что наличие массы покоя связано с взаимодействием электронных и мюонных нейтрино (антинейтрино), так как и наличие фотонов при аннигиляции противоположных частиц связано с взаимодействием этих самых электронных и мюонных нейтрино (антинейтрино), что было нами показано в [2, с. 29-63]. Однако любой объект обладает корпускулярно-волновым дуализмом, то есть наличием в нём взаимодействующих противоположностей через обмен. Иначе нет и самих противоположностей, то есть приходим к однородности и отсутствию возможности различия объектов. А это возможно только через взаимное преобразование корпускулярных свойств в волновые свойства, и наоборот. Поэтому необходимость перехода от волновых свойств к корпускулярным свойствам через математическое описание понимали и сами физики.
. При этом нет ни одного распада на гипотетические гравитоны, кварки, глюоны и виртуальные фотоны. Собственно, это подтверждает идею М. В. Ломоносова, что объект состоит из того, на что он распадается. Физики в своём желании выдачи желаемого за действительное даже не смогли сообразить, что если при аннигиляции электрона и позитрона (а они имеют массу покоя и тем самым должны взаимодействовать через гравитоны) образуются только фотоны, то места для гравитонов нет, как нет и самого способа преобразования гравитонов в электромагнитные волны. Иными словами природа гравитации также должна иметь описание через электромагнитное взаимодействие. Исходя из наблюдаемого практического распада частиц по (1), можно сделать вывод, что наличие массы покоя связано с взаимодействием электронных и мюонных нейтрино (антинейтрино), так как и наличие фотонов при аннигиляции противоположных частиц связано с взаимодействием этих самых электронных и мюонных нейтрино (антинейтрино), что было нами показано в [2, с. 29-63]. Однако любой объект обладает корпускулярно-волновым дуализмом, то есть наличием в нём взаимодействующих противоположностей через обмен. Иначе нет и самих противоположностей, то есть приходим к однородности и отсутствию возможности различия объектов. А это возможно только через взаимное преобразование корпускулярных свойств в волновые свойства, и наоборот. Поэтому необходимость перехода от волновых свойств к корпускулярным свойствам через математическое описание понимали и сами физики.
Однако как показать этот самый переход с сохранением и корпускулярных и волновых свойств, так как ни один объект не может принадлежать только одной из противоположностей? Понятно, что в этом случае существование корпускулярных свойств, характеризующих объект без распада в зависимости от волновых свойств, можно представить только через замкнутый обмен, а это определяется уравнением окружности, которая, как было показано нами в [1, c. 6-42, 2, с. 29-63] связана с уравнением энергии Эйнштейна. Соответственно, вопрос совмещения корпускулярно-волновых свойств в одном объекте с привлечением уравнения энергии Эйнштейна, в котором присутствует как кинетическая, так и потенциальная энергия, и общая энергия инвариантна в любой системе наблюдения, попытался решить Дирак через свою систему уравнений. При этом он использовал так называемую «линеаризацию» уравнения энергии Эйнштейна с переходом от волновых свойств к корпускулярному движению частицы [4, с. 295-296]. Как это будет видно несколько ниже эта «линеаризация» математически выражает представление объекта во взаимодействии более элементарных объектов. То есть, для описания взаимодействия противоположностей на основе корпускулярно-волнового дуализма Дирак интуитивно использовал уравнение энергии Эйнштейна в виде:
| (2) |
Здесь k изменяется от 0 до 3; P0=M0c; P1=Px; P2=Py; P3=Pz. Из этой записи при использовании матриц для разложения:
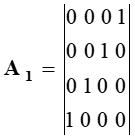 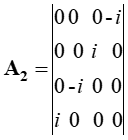 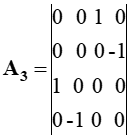 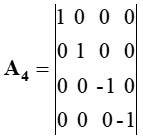 | (3) |
Следуют известные линеаризованные уравнения:
| (4) |
Далее Дирак ввёл операторы Е и р [5, с. 298] с мнимой единицей:
![]() , (5)
, (5)
Которые должны воздействовать на волновую функцию Луи де Бройля Ψ, и которая, в свою очередь, характеризует вероятность. Необходимость использования таких операторов мы показали в [1, с. 6-42]. При этом волновые функции Ψ Луи де Бройля при соответствии уравнению энергии Эйнштейна имеют вид [6, с. 31]:
![]() , (6)
, (6)
В дифференциальном виде мы получим систему уравнений Дирака:
| (7) |
После соответствующей подстановки с выражением одних функций через другие Дираком для функции ![]() было получено решение:
было получено решение:
| (8) |
Соответственно получаем уравнение энергии Эйнштейна в квадрате с учётом функции ![]() :
:
![]() , (9)
, (9)
Иными словами, система уравнений Дирака при переходе во второе уравнение энергии Эйнштейна в квадрате в (2) связана с умножением на волновую функцию Луи де Бройля, что обеспечивает корпускулярно-волновой вид. Собственно, в квантовой механике есть представление на основе релятивистского отображения уравнения энергии Эйнштейна с учётом операторов (5) и в чисто волновом виде [6, с. 31] при волновой функции вида:
![]() , (10)
, (10)
И уравнении:
![]() , (11)
, (11)
В этом случае в качестве решения при наличии массы покоя получается уравнение энергии Эйнштейна в квадрате, которое использовал Дирак в своей системе уравнений, и это не наша выдумка. Однако хоть Дираку и удалось отразить связь волновых свойств с корпускулярными свойствами с переходом к уравнению частицы по формуле энергии Эйнштейна, но он не смог отказаться от волновых функций Луи де Бройля, представленных как характеризующих вероятность, так как вид его уравнений не соответствовал виду обычных уравнений Максвелла с отображением реальных электромагнитных функций. Кроме того, волновой вид связан с распространением в окружающей среде электромагнитных волн, которые характеризуется константами электрической и магнитной проницаемости, а их в уравнении (11) нет (этот парадокс имеет и система измерения СГС). Иными словами, здесь нет влияния окружающей среды на волновое уравнение, а значит, нет соблюдения принципа Гюйгенса – Френеля с изменением направления движения за счёт вторичных источников возбуждения, так как масса покоя электрона (![]() ) – это константа. В итоге получилось, что система уравнений Дирака не имела логичного доказательства, соответствующего практике, а явилась своего рода математическим упражнением с подгонкой под результат. Собственно, это означает, что необходимо привести систему уравнений Дирака в вид, соответствующий реальным физическим законам на основе классической электродинамики с учётом взаимодействия реальных объектов. Соответственно мы помним, что система уравнений Дирака описывает замкнутый обмен между противоположностями объектов с учётом закона сохранения количества.
) – это константа. В итоге получилось, что система уравнений Дирака не имела логичного доказательства, соответствующего практике, а явилась своего рода математическим упражнением с подгонкой под результат. Собственно, это означает, что необходимо привести систему уравнений Дирака в вид, соответствующий реальным физическим законам на основе классической электродинамики с учётом взаимодействия реальных объектов. Соответственно мы помним, что система уравнений Дирака описывает замкнутый обмен между противоположностями объектов с учётом закона сохранения количества.
Так как вероятностные волновые функции не имеют реального воплощения (волновая закономерность и вероятность противоречат друг другу), то, следовательно, необходимо определить, чем обмениваются объекты для взаимодействия для сохранения этих объектов в динамике, и как это должно быть выражено через математические уравнения.
Соответственно, мы должны разрешить парадоксы, представленные выше.
Понятно, что при этом мы должны опираться на математическое описание реальных объектов, которые существует при распаде. В [2, с. 29-63] мы показали, что реальные объекты электронных и мюонных нейтрино (антинейтрино) математически описываются в виде:
| (12) |
Здесь ![]() . Существует также и комплексно-сопряжённая форма записи этих уравнений. Вид в частных производных выбран потому, что при представлении в векторном виде необходимость проекции электромагнитных составляющих на время (это означает подчинение электромагнитных составляющих преобразованиям по СТО и ОТО Эйнштейна) не видна. Одновременно, как мы уже отмечали, необходимо учитывать комплексное представление констант электрической и магнитной проницаемости, что также в классическую электродинамику было введено до нас. При этом наличие четырёх производных в одном уравнении это минимально необходимый вид математического описания взаимодействия противоположностей, что игнорировалось в обычных уравнениях Максвелла (всего три члена). И вот с учётом сказанного можно представить усовершенствованные уравнения Максвелла и в векторном виде:
. Существует также и комплексно-сопряжённая форма записи этих уравнений. Вид в частных производных выбран потому, что при представлении в векторном виде необходимость проекции электромагнитных составляющих на время (это означает подчинение электромагнитных составляющих преобразованиям по СТО и ОТО Эйнштейна) не видна. Одновременно, как мы уже отмечали, необходимо учитывать комплексное представление констант электрической и магнитной проницаемости, что также в классическую электродинамику было введено до нас. При этом наличие четырёх производных в одном уравнении это минимально необходимый вид математического описания взаимодействия противоположностей, что игнорировалось в обычных уравнениях Максвелла (всего три члена). И вот с учётом сказанного можно представить усовершенствованные уравнения Максвелла и в векторном виде:
| (13) |
Собственно, ничего нового мы здесь фактически не придумали, мы лишь явно обозначили то, что уже использовалось в физике. Особый интерес здесь представляют сторонние плотности зарядов и токов (![]() ), которые были также введены до нас в классической электродинамике. Как было показано в квантовой механике [7, с. 300], исходя из условия инвариантности (это закон сохранения количества, то есть законов физики, в любой системе наблюдения), эти плотности сторонних токов и зарядов должны подчиняться преобразованиям Лоренца – Минковского в виде:
), которые были также введены до нас в классической электродинамике. Как было показано в квантовой механике [7, с. 300], исходя из условия инвариантности (это закон сохранения количества, то есть законов физики, в любой системе наблюдения), эти плотности сторонних токов и зарядов должны подчиняться преобразованиям Лоренца – Минковского в виде:
| (14) |
Здесь: ![]() . Однако в квантовой механике подразумевалось, что данные преобразования связаны с реальной скоростью (
. Однако в квантовой механике подразумевалось, что данные преобразования связаны с реальной скоростью (![]() ) по СТО Эйнштейна в нашей системе наблюдения. При этом самих сторонних токов и зарядов в нашей системе наблюдения не наблюдается и скорость тока равна скорости света, что исключает наличие объектов движения с массой покоя. Одновременно среда распространения электромагнитных волн, которые однозначно связаны с уравнениями Максвелла, описывается через константы электрической и магнитной проницаемости, и это реальные параметры среды и ничего другого в описании среды нет. Соответственно в [2, с. 29-63], была показана необходимость, с целью исключения парадоксов (например, константы электрической и магнитной проницаемости не выражались как противоположности, и отличались только по величине в системе измерения СИ), представлять константы электрической и магнитной проницаемости как величины, связанные с общей кинетической скоростью объектов, но в противоположной системе наблюдения, при условии термодинамического равновесия, на основе чего по ОТО Эйнштейна формируется изменение среды через пространственно-временное искривление. Отсюда, следует выразить константы магнитной и электрической проницаемости через усреднённое (интегральное) движение частиц, со скоростью (кинетической энергией) в противоположной системе наблюдения (в нашей системе наблюдения это проекция скорости на время)
) по СТО Эйнштейна в нашей системе наблюдения. При этом самих сторонних токов и зарядов в нашей системе наблюдения не наблюдается и скорость тока равна скорости света, что исключает наличие объектов движения с массой покоя. Одновременно среда распространения электромагнитных волн, которые однозначно связаны с уравнениями Максвелла, описывается через константы электрической и магнитной проницаемости, и это реальные параметры среды и ничего другого в описании среды нет. Соответственно в [2, с. 29-63], была показана необходимость, с целью исключения парадоксов (например, константы электрической и магнитной проницаемости не выражались как противоположности, и отличались только по величине в системе измерения СИ), представлять константы электрической и магнитной проницаемости как величины, связанные с общей кинетической скоростью объектов, но в противоположной системе наблюдения, при условии термодинамического равновесия, на основе чего по ОТО Эйнштейна формируется изменение среды через пространственно-временное искривление. Отсюда, следует выразить константы магнитной и электрической проницаемости через усреднённое (интегральное) движение частиц, со скоростью (кинетической энергией) в противоположной системе наблюдения (в нашей системе наблюдения это проекция скорости на время) ![]() , связанной с нашей системой наблюдения через скорость света. Иными словами, по ОТО мы имеем абсолютную систему наблюдения за счёт проекции скорости на время. И в этом случае мы имеем константы электрической и магнитной проницаемости в виде:
, связанной с нашей системой наблюдения через скорость света. Иными словами, по ОТО мы имеем абсолютную систему наблюдения за счёт проекции скорости на время. И в этом случае мы имеем константы электрической и магнитной проницаемости в виде:
| (15) |
Кроме того, нам известно, что Дирак использовал для своей системы уравнений формулу энергии Эйнштейна для соблюдения закона сохранения количества, а в ней под величину зарядов не предусмотрено энергии и соответственно поэтому заряды не могут выражать какое-либо воздействие. Для этого надо иметь реальное воплощение, а это без энергии не бывает. Отсюда заряды не могут выступать как дробные величины (как это принято сейчас физиками), и по теории Дирака мы имеем: ![]() . Таким образом, для описания плотности сторонних зарядов и токов остаётся только одно представление в виде длины и времени в противоположной системе наблюдения с учётом выполнения в этой системе наблюдения преобразований по СТО и ОТО Эйнштейна. Отсутствие симметрии при преобразовании означало бы нарушение закона сохранения количества между противоположностями. Собственно, аналогичную интерпретацию для зарядов ввёл, и Фейнман [8, с. 273] при описании относительности представления электрических и магнитных полей в зависимости от системы наблюдения для плотности зарядов, связав их законом действительным для преобразований Лоренца в виде:
. Таким образом, для описания плотности сторонних зарядов и токов остаётся только одно представление в виде длины и времени в противоположной системе наблюдения с учётом выполнения в этой системе наблюдения преобразований по СТО и ОТО Эйнштейна. Отсутствие симметрии при преобразовании означало бы нарушение закона сохранения количества между противоположностями. Собственно, аналогичную интерпретацию для зарядов ввёл, и Фейнман [8, с. 273] при описании относительности представления электрических и магнитных полей в зависимости от системы наблюдения для плотности зарядов, связав их законом действительным для преобразований Лоренца в виде:
| (16) |
Здесь ![]() – относительная скорость по СТО Эйнштейна,
– относительная скорость по СТО Эйнштейна, ![]() – плотность заряда. Соответственно произведение плотности зарядов подчиняется инвариантной форме. При этом подчинение преобразованиям Лоренца – Минковского осуществляется как для СТО, так и для ОТО Эйнштейна. В этом случае мы имеем симметрию в выполнении законов в противоположных системах наблюдения, связанных через скорость света. А это говорит о том, что заряды (электрон и позитрон) в нашей системе наблюдения выражаются также через объекты длины и времени.
– плотность заряда. Соответственно произведение плотности зарядов подчиняется инвариантной форме. При этом подчинение преобразованиям Лоренца – Минковского осуществляется как для СТО, так и для ОТО Эйнштейна. В этом случае мы имеем симметрию в выполнении законов в противоположных системах наблюдения, связанных через скорость света. А это говорит о том, что заряды (электрон и позитрон) в нашей системе наблюдения выражаются также через объекты длины и времени.
Следовательно, с учётом начальной связи длины и времени (l=ct) [9, с. 225-226] и однозначной заменой сторонних зарядов на параметры длины и времени, мы имеем уравнения:
| (17) |
Собственно иное представление зарядов привело к тому, что они не имели бы взаимодействия с пространством и временем, а значит и не могли передавать через пространство и время взаимодействие через обмен, так как нет механизма преобразования.
Повторим, что в среде распространения мы движущихся электрических зарядов не наблюдаем, а значит, нет причины говорить об их плотности с подчинением СТО Эйнштейна. Иными словами, электрическим зарядам на основе электрона и позитрона в среде распространения должна быть замена с подчинением ОТО Эйнштейна. Если предположить объекты не связанные со средой распространения с характеристикой вне пространства и времени, то разные объекты должны иметь и отличие по подчинению законам физики, с механизмом преобразования, так как иначе не будет и самих различий. А раз различий в подчинении законам физики нет, то следует признать объекты идентичными. Иными словами, мы представили сторонние плотности электрических и магнитных зарядов на то, что реально существует на практике при математическом описании и уже было представлено в качестве условия необходимости относительности электрических и магнитных полей. То есть, это длина и время, приведённые в одну систему наблюдения с учётом ОТО Эйнштейна, где v связано с кинетической энергией в противоположности. При этом сторонние электрические и магнитные заряды отражают эквиваленты противоположных зарядов с выражением через объекты длины и времени. Собственно ничего нового мы здесь не придумали так как объекты мироздания выражаются, с отражением своего существования, через взаимодействие противоположностей, и это отражается в виде подчинения преобразований этих объектов в одной системе наблюдения на основании СТО, а в другой системе наблюдения это интерпретируется как подчинение преобразованиям по ОТО Эйнштейна с соответствующей заменой объектов длины на время, и наоборот. Таким образом, все члены в усовершенствованных уравнениях Максвелла имеют логику реального воплощения на основе взаимодействия противоположностей, и физикам надо было лишь признать то, что они сами уже давно ввели в классическую электродинамику.
Как показано в [2, с. 29-63], исходя из взаимодействия усовершенствованных уравнений Максвелла, характеризующих электронные и мюонные нейтрино (антинейтрино), через операцию изменения в виде ротора (rot), был получен вид для волновых уравнений на основе сторонних токов:
| (18) |
С учётом перехода от сторонних зарядов на сторонние токи по (13) имеем:
| (19) |
Здесь мнимая единица учитывает, что проекция на время и проекции по координатам – это противоположности, что соответствует комплексному представлению констант электрической и магнитной проницаемости по классической электродинамике. В результате мы имеем, что волновые процессы, характеризующие обмен, в одной противоположности связаны с движением объектов длины и времени, выраженных через плотности сторонних токов и зарядов, в другой противоположности. Однако данный вид не совпадает с уравнением волны с вынужденным источником излучения (поглощения) по (11), хотя справа от знака равенства рассматриваются реальные процессы выполнения законов электродинамики. Эта проблема решается если учесть, что по законам электродинамики противоположностью в соответствующей системе наблюдения к электромагнитным составляющим выступают векторные потенциалы, которые отражают статические значения электромагнитных составляющих через динамику изменения векторных потенциалов. Причём векторный потенциал А должен удовлетворять условию ![]() (это и есть неизменность по пространству с представлением в виде замкнутой величины), что достигалось посредством следующего уравнения [10, с. 118]:
(это и есть неизменность по пространству с представлением в виде замкнутой величины), что достигалось посредством следующего уравнения [10, с. 118]:
![]() , (20)
, (20)
Понятно, что при определении дивергенции от замкнутой величины в виде ротора мы будем иметь ноль. И отсюда запись (20) выглядит парадоксальной, так как тогда и ![]() . Однако это противоречие разрешимо, если считать, что слева и справа от знака равенства рассматриваются противоположности, и замкнутость в одной противоположности соответствует разомкнутости в другой противоположности. Подстановка этого выражения в уравнение
. Однако это противоречие разрешимо, если считать, что слева и справа от знака равенства рассматриваются противоположности, и замкнутость в одной противоположности соответствует разомкнутости в другой противоположности. Подстановка этого выражения в уравнение 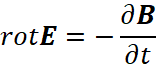 даёт уравнение:
даёт уравнение:
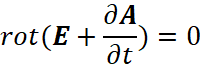 , (21)
, (21)
Чтобы удовлетворить этому уравнению выражение в скобках приравнивалось к величине градиента потенциальной функции, что исключало замкнутость, то есть имеем уравнение:
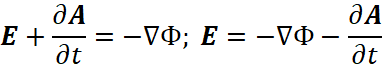 , (22)
, (22)
В этом случае векторный потенциал А характеризовал замкнутые процессы при изменении по пространству, а векторный потенциал Ф, наоборот, определял разомкнутые процессы по пространству. Иными словами, А и Ф характеризуют противоположности по пространству.
Для непосредственной связи векторных потенциалов мы учитываем известную формулу из электродинамики [11, с. 165]:
![]() , (23)
, (23)
Можно считать, что эта формула по гипотезе Луи де Бройля фактически вытекает из формулы по необходимости обратно-пропорциональной связи противоположностей ![]() , с учётом соответствующей нормировки к единице. При этом принимаем, что v=c, и тогда векторные потенциалы А и Ф связаны так же, как компоненты электрического и магнитного поля по уравнению Н=сЕ, и характеризуют именно электромагнитное поле, но в противоположности. В этом случае величина Е по формуле (22) характеризуется в одинаковом количественном представлении с учётом r=ct в виде:
, с учётом соответствующей нормировки к единице. При этом принимаем, что v=c, и тогда векторные потенциалы А и Ф связаны так же, как компоненты электрического и магнитного поля по уравнению Н=сЕ, и характеризуют именно электромагнитное поле, но в противоположности. В этом случае величина Е по формуле (22) характеризуется в одинаковом количественном представлении с учётом r=ct в виде:
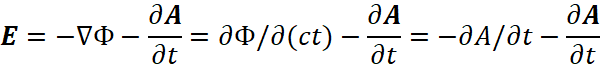 , (24)
, (24)
Далее, исходя из Н=сЕ (а это закон связи противоположностей через скорость обмена, которая равна скорости света, так как в противном случае между Е и Н нет отличий, а значит мы имеем парадокс отсутствия противоположностей), мы при замене электромагнитных составляющих на уравнения вектор – потенциалов, что соответствует смене системы наблюдения на противоположную, имеем:
| (25) |
С учётом (24) мы видим, что физики интуитивно уже ввели правило общего закона мироздания, когда сложение в одной противоположности означает вычитание в другой противоположности, что было нами представлено на основе преобразований по СТО в виде [1, с. 6-42]:
| (26) |
Если рассматривать взаимосвязь глобальных противоположностей через скорость света (обмена), то vx=c, и в этом случае ![]() . Данный закон при сохранении количественного равенства (а это непременное условие существования самого объекта) возможно реализовать только через наличие закономерностей в виде:
. Данный закон при сохранении количественного равенства (а это непременное условие существования самого объекта) возможно реализовать только через наличие закономерностей в виде:
cos2(x)+sin2(x)=ch2(w) – sh2(w) =1= const, exp(ix)exp(-ix)=exp(w)exp(-w) =1. | (27) |
Здесь w=(-1)1/2x. Иными словами, выполнение законов по преобразованиям СТО и ОТО Эйнштейна определяет и вид функций для объектов мироздания.
Как будет показано ниже для системы наблюдения из противоположности объектов с учётом выполнения ОТО Эйнштейна значение vx относится к проекции на время и связано с константами электрической и магнитной проницаемости.
Соответственно для значений Е и Н не остаётся иного физического аналога кроме как времени и пространства (при наблюдении из противоположности), которые тоже связаны при условии соблюдения СТО (а это закон сохранения количества) по преобразованиям Минковского в виде r=ct. Учитывая, что векторное отображение не определяет ортогональности противоположностей, какими являются А и Ф, которые аналогичны Е и Н, мы должны уравнение (25) расписать по частным производным аналогично тому, как это сделано для электромагнитных составляющих. В результате получим:
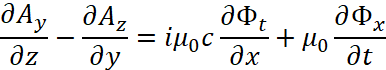 , (28)
, (28)
Таким образом, мы видим, что векторные потенциалы отражают аналогичные законы электродинамики, но в противоположной системе наблюдения.
Далее мы учтём, что воздействие одной противоположности осуществляется на объект, представленный через другую противоположность. Отсюда мы делаем подстановку уравнения (21) с заменой напряжённости электрического поля на векторные потенциалы и получим:
| (29) |
Такое действие используется в математике при переходе к выражению с одним видом функции через подстановку, и как было показано выше, этот метод применил и Дирак.
По нашей теории любое изменение означает переход в противоположность со сменой системы наблюдения и с заменой сложения на вычитание, и наоборот. Для величины векторного потенциала ![]() противоположностью для перехода является векторный потенциал
противоположностью для перехода является векторный потенциал ![]() с условием выполнения количественного равенства. Собственно, это правило интуитивно ввели в электродинамику физики, и отсюда в классической электродинамике в противовес уравнению (22) в одной противоположности, физики были вынуждены ввести калибровку Лоренца, отражающую процессы в другой противоположности со сменой переменных дифференцирования из-за смены системы наблюдения в виде [12, с. 119]:
с условием выполнения количественного равенства. Собственно, это правило интуитивно ввели в электродинамику физики, и отсюда в классической электродинамике в противовес уравнению (22) в одной противоположности, физики были вынуждены ввести калибровку Лоренца, отражающую процессы в другой противоположности со сменой переменных дифференцирования из-за смены системы наблюдения в виде [12, с. 119]:
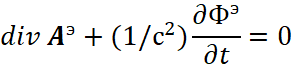 , (30)
, (30)
В итоге, было получено волновое уравнение в зависимости от так называемой плотности заряда в классической электродинамике в виде:
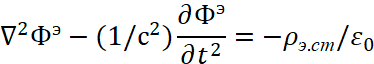 , (31)
, (31)
Физически это означает, что изменение напряжённости поля в пространстве с учётом электрической проницаемости в одной противоположности формирует волновые процессы в другой противоположности. То есть статичный объект, представляющийся величиной ![]() , в одной противоположности надо рассматривать как волновой процесс с излучением и поглощением в другой противоположности.
, в одной противоположности надо рассматривать как волновой процесс с излучением и поглощением в другой противоположности.
Если учесть связь между векторным потенциалом А и Ф по формуле (23) с учётом v=c (![]() ), то получим второе известное уравнение для векторного потенциала А в классической электродинамике в виде [12, с. 119]:
), то получим второе известное уравнение для векторного потенциала А в классической электродинамике в виде [12, с. 119]:
| (32) |
Таким образом, так как противоположности связаны через скорость света, сторонняя плотность заряда в одной противоположности формирует волновую составляющую ![]() , а в другой противоположности это рассматривается как формирование волновой составляющей
, а в другой противоположности это рассматривается как формирование волновой составляющей ![]() под влиянием сторонней плотности тока. Напомним, что, в силу того, что существует закон сохранения заряда в соответствии с теорией Дирака (
под влиянием сторонней плотности тока. Напомним, что, в силу того, что существует закон сохранения заряда в соответствии с теорией Дирака (![]() ) и значение заряда не входит в формулу энергии Эйнштейна, а значит и не может быть самостоятельной величиной воздействия из-за отсутствия энергии (количества), то изменение сторонних (фиктивных) плотности заряда и плотности тока связано только с подчинением преобразованиям Лоренца – Минковского (14), и другого способа их изменения не предвидится. Отсюда следует вывод, что по уравнениям (31) и (32) изменение сторонней плотности заряда и плотности тока связано с константами электрической и магнитной проницаемости, которые также должны быть представлены в параметрах длины и времени.
) и значение заряда не входит в формулу энергии Эйнштейна, а значит и не может быть самостоятельной величиной воздействия из-за отсутствия энергии (количества), то изменение сторонних (фиктивных) плотности заряда и плотности тока связано только с подчинением преобразованиям Лоренца – Минковского (14), и другого способа их изменения не предвидится. Отсюда следует вывод, что по уравнениям (31) и (32) изменение сторонней плотности заряда и плотности тока связано с константами электрической и магнитной проницаемости, которые также должны быть представлены в параметрах длины и времени.
Следует отметить, что уравнения (31) и (32) не имеют решения в волновом виде с точки зрения распространяющейся волны с источниками возбуждения, так как для решения в волновом виде уравнение частицы с массой покоя должно иметь вид (11) с решением в виде функции Луи де Бройля (10), где в правой и левой части уравнения присутствует функция ![]() . Однако решения уравнений (31) и (32) соответствуют варианту взаимодействия со средой распространения через константы электрической и магнитной проницаемости с очевидным результатом для векторного потенциала Ф в виде:
. Однако решения уравнений (31) и (32) соответствуют варианту взаимодействия со средой распространения через константы электрической и магнитной проницаемости с очевидным результатом для векторного потенциала Ф в виде:
![]() , (33)
, (33)
В квантовой механике это было представлено в виде функции ![]() . Разница касается лишь того, что в нашем случае константы электрической и магнитной проницаемости это параметры зависящие от среды распространения, что, собственно, и обеспечивает выполнение принципа Гюйгенса-Френеля, так как в противном случае нет величины, дающей изменение направления волны. Для векторного потенциала
. Разница касается лишь того, что в нашем случае константы электрической и магнитной проницаемости это параметры зависящие от среды распространения, что, собственно, и обеспечивает выполнение принципа Гюйгенса-Френеля, так как в противном случае нет величины, дающей изменение направления волны. Для векторного потенциала ![]() имеем решение:
имеем решение:
![]() , (34)
, (34)
При этом необходимо помнить, что аргументы функций в силу закона сохранения количества между противоположностями должны подчиняться условию:
| (35) |
Собственно данное условие равенства нулю аргумента функции связано с выполнением формулы Луи де Бройля [13, с. 62-63], что видно из преобразований в виде:
| (36) |
Последнее равенство говорит о том, что скорость и длина выступают как противоположности с учётом обратно-пропорциональной связи между ними. Следовательно, это означает что закон связи для констант мироздания ch=1 полученный нами в [1, с. 6-42] действителен для любых объектов мироздания и связан с выполнением закона по формуле Луи де Бройля. В этом случае мы имеем:
| (37) |
Иными словами, это означает, что в системе наблюдения от аргументов функций значения энергии и импульсов отличаются от энергии и импульсов в системе наблюдения после решения уравнений (31) и (32). Такая разница связана с иерархическим построением мироздания с исключением замкнутого цикла с обратным возвращением на тот же уровень и возможностью создания вечного двигателя.
В силу того, что аргумент волновых функций из-за условия выполнения формулы Луи де Бройля (36) равен нулю, то мы можем использовать умножение и правых частей от знака равенства в уравнениях (31) и (32) на соответствующие волновые функции, аналогично тому как это сделал Шредингер и Дирак в квантовой механике [6, с. 31]:
| (38) |
В результате мы имеем выражение единого объекта через две волновые составляющие Аэ и Фэ. При этом мы имеем противоположные системы наблюдения для векторных потенциалов со связью через скорость света, а это означает их ортогональность. Так как процессы в противоположностях симметричны, то такой вид волн действителен и для электромагнитных составляющих. Однако здесь необходимо учесть, что в данном случае был использован только один вид стороннего электрического заряда и соответственно напряжённость электрического поля волны в одной противоположности представляется напряжённостью магнитного поля волны в другой противоположности, что соответствует электромагнитному континууму с преобразованием друг в друга электрических и магнитных компонент. То есть Аэ и Фэ представляют одну и ту же составляющую от одного стороннего электрического заряда (плотности), но в противоположностях. В реальности для исключения парадокса отсутствия закона сохранения количества из-за несимметричных уравнений мы имеем взаимодействие сторонних электрических и магнитных зарядов (это противоположности) с образованием электромагнитной волны, к чему также интуитивно пришли и физики в классической электродинамике. Поэтому. в силу того, что мы имеем и сторонний магнитный (противоположный) заряд (это следует из симметрии составляющих в электромагнитной волне и введено до нас), то для него тоже должны существовать магнитные векторные потенциалы в виде [14, с. 118]:
![]() , (39)
, (39)
Отсюда с учётом изменения в пространстве магнитной составляющей с учётом ![]() имеем волновые уравнения вида:
имеем волновые уравнения вида:
| (40) |
Эти уравнения с учётом, введённого Шредингером и Дираком умножения справа от знака равенства на волновую функцию, имеет вид:
| (41) |
В результате получаем решения аналогичные по виду (10):
| (42) |
Иными словами, мы получаем, что константы электрических и магнитных проницаемостей меняются местами в зависимости от того, какая плотность стороннего заряда рассматривается.
В итоге мы имеем, что формирование волновых процессов на основе векторных потенциалов в противоположности также связаны с константами электрической и магнитной проницаемости, которые фактически отражают объекты длины и времени (противоположные сторонние заряды).
Так как плотности электрических и магнитных зарядов (противоположных зарядов), согласно корпускулярно-волновому представлению любого объекта, отражаются в обеих противоположностях, то здесь с учётом зависимостей для векторных потенциалов, введённых в классической электродинамике [15, с. 39], аналогично законам электродинамики по уравнениям Максвелла, мы имеем образование напряжённостей электрических и магнитных полей в среде распространения как результат от сумм воздействия уравнений:
| (43) |
Сравнивая (19) и (43), мы видим, что эти уравнения как бы отражают вид волнового уравнения (11), где левая часть уравнения (19) отражает левую часть уравнения (11), а левая часть уравнения (42) отражает правую часть уравнения (11). Полная идентичность будет достигнута, если векторные потенциалы ![]() и
и ![]() , преобразовать к векторным потенциалам
, преобразовать к векторным потенциалам ![]() и
и ![]() .
.
Отсюда, в соответствии с классической электродинамикой мы должны учесть равенство приращений [16, с. 36-37]:
| (44) |
После интегрирования по пространству с учётом введённой в квантовой механике зависимости виде r=ict [17, с. 317] при отсутствии в среде распространения внешних воздействий следуют равенства:
| (45) |
Иными словами, физики в классической электродинамике утвердили интуитивно связь векторных потенциалов на основе констант электрической и магнитной проницаемости. Нам лишь оставалось указать связь этих констант в соответствии с ОТО Эйнштейна с кинетической энергией в противоположности по (15) с целью исключения парадоксов.
Согласно Фейнману [18, с. 271] мы имеем, помимо проекций векторных потенциалов на длину, их проекции на время, в соответствии с СТО и ОТО Эйнштейна. Соответственно после подстановки полученных выражений в последние два уравнения в (43) имеем:
| (46) |
Таким образом мы видим, что правые части уравнений (19) и (46) аналогичны, а левые части описывают уравнение волны с учётом источника излучения (поглощения). Собственно, сам процесс образования волновых процессов в противоположности на основании электрической и магнитной индукции, с наличием констант электрической и магнитной проницаемости, был также рассмотрен в классической электродинамике.
Повторим логику, приведённую физиками [19, с. 124].
В этом случае физики ввели электрическую поляризованность Р и намагниченность М в системе МКСА в виде:
| (47) |
Далее в классической электродинамике считают, что:
| (48) |
В таком случае электромагнитные потенциалы Ф и А могут быть найдены из уравнений:
| (49) |
Собственно разное математическое представление для векторных потенциалов и рассмотренных ниже электрических и магнитных векторов Герца отражает также различие представления в зависимости от системы наблюдения. Это принципиальное отличие физики от математики, в которой воздействие не рассматривается как новое представление объекта из-за преобразования. Здесь, при учёте выполнения условия Лоренца, физики ввели электрический (П) и магнитный (Z) векторы Герца, связав их математически с векторными потенциалами через подстановку:
| (50) |
Отличие (50) от (48) в том, что плотность заряда и плотность тока меняется на векторные потенциалы, в то время как выше мы показали волновой характер зависимости векторных потенциалов от плотности заряда и тока. Иными словами, физики интуитивно до нас ввели условие симметрии в противоположностях и утвердили правило, при котором представление объекта зависит от системы наблюдения. Тогда верхнее уравнение (49) приводится к следующему виду:
| (51) |
На следующем шаге учитывают, что одинаковые изменения по дивергенции не влияют на закон сохранения количества, и отсюда получают:
![]() , (52)
, (52)
Второе уравнение в (49) с учётом второго уравнения в (50) приводится к виду:
| (53) |
Из уравнения (52) следует, что:
![]() , (54)
, (54)
Здесь, а – произвольный вектор. Тогда второе уравнение из (53) сводится к следующему виду:
![]() , (55)
, (55)
Из него, в свою очередь, вытекает, что:
![]() , (56)
, (56)
Здесь ![]() – также произвольный скаляр.
– также произвольный скаляр.
Так как при изменениях в дифференциальном виде подстановка ![]() , и
, и ![]() не меняет зависимости от источников
не меняет зависимости от источников ![]() и
и ![]() , то в системе МКСА имеем:
, то в системе МКСА имеем:
| (57) |
При выражении через напряжённости электрических и магнитных полей мы имеем:
| (58) |
Соответственно для внешней среды ![]() , мы имеем:
, мы имеем:
| (59) |
С учётом П=сZ, что действительно для электрической и магнитной компоненты вида Н=сЕ, мы видим, что в системе уравнений (59) электромагнитные составляющие, которые способны перемещаться со скоростью света, имеют обратно - пропорциональную зависимость от константы электрической проницаемости. Таким образом волновые процессы как в случаях для векторных потенциалов (38) и (40), так и в случае волн для электрического и магнитного векторов Герца (59), определяются константами электрической и магнитной проницаемости. Соответственно, из-за разницы в математическом представлении от констант электрической проницаемости и магнитной проницаемости мы имеем различие в системе наблюдения. Поэтому константы электрической и магнитной проницаемости могут рассматриваться с учётом смены представления в зависимости от системы наблюдения, как это было введено для длины и времени Эйнштейном на основе его СТО и ОТО. Таким образом, мы показали, что волновые напряжённости электромагнитных полей в одной противоположности выражаются объектами на основе констант электрической и магнитной проницаемости, которые по предлагаемой теории подчиняются преобразованиям Лоренца с учётом ОТО Эйнштейна (15), и фактически являются эквивалентами пространственно-временного искривления среды распространения.
В результате с учётом характеристик напряжённостей полей на основе констант электрической и магнитной проницаемости имеем:
| (60) |
Суть замены Н на ![]() , связан с переходом справа в иную систему наблюдения, так как константы электрической и магнитной проницаемости определяются преобразованиями Лоренца, аналогично тому, как это фактически ввели сами физики на основе равенств (44) и (45). Далее мы должны учесть, что значения по координатам имеют связь как напряжённости электрических и магнитных полей со связью Н=сЕ, что следовало из идентичности усовершенствованных уравнений Максвелла с уравнениями для векторных потенциалов [20, с. 40-56]. Это, по сути, означало, что векторные потенциалы отображают электромагнитные свойства, но в противоположной системе наблюдения. Отсюда мы вводим аналогичную связь в виде
, связан с переходом справа в иную систему наблюдения, так как константы электрической и магнитной проницаемости определяются преобразованиями Лоренца, аналогично тому, как это фактически ввели сами физики на основе равенств (44) и (45). Далее мы должны учесть, что значения по координатам имеют связь как напряжённости электрических и магнитных полей со связью Н=сЕ, что следовало из идентичности усовершенствованных уравнений Максвелла с уравнениями для векторных потенциалов [20, с. 40-56]. Это, по сути, означало, что векторные потенциалы отображают электромагнитные свойства, но в противоположной системе наблюдения. Отсюда мы вводим аналогичную связь в виде ![]() . При этом, напомним, что для значения
. При этом, напомним, что для значения ![]() , мы не имеем проекции на длину в силу перпендикулярности значений
, мы не имеем проекции на длину в силу перпендикулярности значений ![]() и
и ![]() по аналогии с Е и Н, а это означает, что в системе наблюдения это может быть только проекция на время согласно идее Фейнмана [18, с. 271]. В этом случае при замене с приведением к корпускулярному виду в одной общей системе наблюдения через значение
по аналогии с Е и Н, а это означает, что в системе наблюдения это может быть только проекция на время согласно идее Фейнмана [18, с. 271]. В этом случае при замене с приведением к корпускулярному виду в одной общей системе наблюдения через значение ![]() , с наличием проекций по трём координатам, аналогично тому как мы это делали выше для перехода от векторного потенциала Ф к векторному потенциалу А в (45), необходимо поменять систему наблюдения для
, с наличием проекций по трём координатам, аналогично тому как мы это делали выше для перехода от векторного потенциала Ф к векторному потенциалу А в (45), необходимо поменять систему наблюдения для ![]() с условием
с условием ![]() , так как проекции длины и времени подчиняются СТО и ОТО Эйнштейна. Соответственно значение
, так как проекции длины и времени подчиняются СТО и ОТО Эйнштейна. Соответственно значение ![]() выразим через значение
выразим через значение ![]() в виде
в виде ![]() , что говорит о противоположности величин по аналогии с равенством, введённым в квантовой механике iФ=А4 [17, с. 317]. Соответственно получаем:
, что говорит о противоположности величин по аналогии с равенством, введённым в квантовой механике iФ=А4 [17, с. 317]. Соответственно получаем:
| (61) |
Переход к одной общей функции характеризует корпускулярно-волновой объект. По сути, два члена с мнимой единицей при равенстве ![]() , а также равенство
, а также равенство ![]() характеризуют известные обычные уравнения Максвелла наблюдаемые на практике для описания объекта в статике и динамике. В этом случае наличие статического объекта в одной противоположности поддерживается за счёт динамики изменения в другой противоположности. Одновременно, так как противоположности по СТО и ОТО Эйнштейна имеют обратно-пропорциональную связь, то для напряжённости электрического поля мы имеем зависимость от константы электрической проницаемости с переходом к новой переменной в виде
характеризуют известные обычные уравнения Максвелла наблюдаемые на практике для описания объекта в статике и динамике. В этом случае наличие статического объекта в одной противоположности поддерживается за счёт динамики изменения в другой противоположности. Одновременно, так как противоположности по СТО и ОТО Эйнштейна имеют обратно-пропорциональную связь, то для напряжённости электрического поля мы имеем зависимость от константы электрической проницаемости с переходом к новой переменной в виде ![]() . Здесь знак минус учитывает противодействие на действие, что также было использовано в системе уравнений Максвелла при преобразовании электромагнитных полей друг в друга. В этом случае общая энергия от смены системы наблюдения по закону сохранения количества не меняется
. Здесь знак минус учитывает противодействие на действие, что также было использовано в системе уравнений Максвелла при преобразовании электромагнитных полей друг в друга. В этом случае общая энергия от смены системы наблюдения по закону сохранения количества не меняется ![]() , но соблюдается условие противодействия на действие при инвариантности. Отсюда имеем:
, но соблюдается условие противодействия на действие при инвариантности. Отсюда имеем:
| (62) |
При этом мы видим, что инвариантность соблюдается и для проекций на время ![]() . Следовательно, мы получаем два уравнения относительно одной переменной в виде:
. Следовательно, мы получаем два уравнения относительно одной переменной в виде:
| (63) |
Таким образом, мы показали, что вид представления зависит от системы наблюдения с подчинением при этом преобразованиям по СТО и ОТО Эйнштейна. Понятно, что само преобразование – это не самоцель и главная задача – это показать, как это преобразование соответствует практике перехода от волновых свойств к корпускулярным свойствам. Если взаимодействие электронных и мюонных нейтрино и антинейтрино с превращением в электромагнитные волны нами было показано в [2, с. 29-63], то теперь необходимо показать превращение электромагнитной волны в виде фотона в электрон и позитрон при столкновении фотона с препятствием. Так как препятствие при этом не теряет свой вид, то отсюда следует вывод, что для превращения электромагнитной волны в позитрон и электрон существуют только компоненты этой электромагнитной волны. Соответственно при столкновении с препятствием имеются, помимо компонент падающей волны, компоненты отражённой волны (в итоге имеем четыре уравнения), и здесь чудес нет. В этом случае с учётом закона сохранения количества может быть только новая взаимосвязь этих компонент для образования электрона и позитрона. Мы видим, что вид уравнений в (63) практически совпадает с видом уравнений в системе Дирака за исключением наличия константы в виде массы покоя электрона (позитрона) и коэффициента ![]() , который характеризует среду распространения. Поэтому теперь необходимо понять, каким образом происходит преобразование массы покоя с учётом корпускулярно-волнового дуализма. При этом мы учитываем, что никакой отдельной массы покоя не существует, а влияние объекта всегда выражается через его силовое воздействие на другие объекты, что представляется через пространственно-временное искривление, а также через электрические и магнитные силы, так как ничего другого и нет.
, который характеризует среду распространения. Поэтому теперь необходимо понять, каким образом происходит преобразование массы покоя с учётом корпускулярно-волнового дуализма. При этом мы учитываем, что никакой отдельной массы покоя не существует, а влияние объекта всегда выражается через его силовое воздействие на другие объекты, что представляется через пространственно-временное искривление, а также через электрические и магнитные силы, так как ничего другого и нет.
Как мы отмечали выше, так как объекты сохраняются и существует симметрия законов в противоположностях (иначе чудеса), то вместо электрических и магнитных сторонних токов, характеризующих электромагнитную волну, можно ввести векторные потенциалы, исходя из идентичности законов в противоположностях.
Здесь учитывается, что если для формирования магнитного или электрического волнового процесса в нашей системе наблюдения требовалась динамика изменения так называемых электрических и магнитных сторонних токов (19), то в противоположной системе наблюдения уже сам сторонний электрический или магнитный ток выступает источником формирования волновых процессов в противоположности [2, с. 29-63]:
| (64) |
Если расписать систему уравнений (63) с учётом h=m0=1/c, а также, что ![]() , то мы получим:
, то мы получим:
| (65) |
С учётом умножения уравнений на мнимую единицу будем иметь:
| (66) |
В соответствии с системой Дирака (7), мы должны представить уравнения (66) в частных производных в зависимости аргумента функций по соответствующим переменным. Понятно, что волновая функция Аэ в каждом случае соответствующих производных по координатам длины и времени должна соответствовать волновым функциям Ψ в системе уравнений Дирака по условию закона сохранения количества при преобразованиях. Распишем уравнения в (66) в частных производных по координатам длины и времени в виде:
| (67) |
Видно, что первое уравнение в (67) отличается по виду от первого и второго уравнения в системе Дирака (7), которые имеют вид:
| (68) |
Здесь разница между функциями в том, что вместо значения в скорость света (с), присутствует величина (u=(c2-vпр2)1/2) и есть разница в знаках первого уравнения в (67) с первым уравнением в системе Дирака (68).
Аналогично и второе уравнение в (67) отличается по виду от третьего и четвёртого уравнений в системе Дирака, которые имеют вид:
| (69) |
Здесь также есть разница в знаках и есть разница между функциями в том, что вместо значения в скорость света (с), присутствует величина (c2/u=( c2/c2-vпр2)1/2). И это разница связана с тем, что в системе уравнений Дирака на основе волновых функций, характеризующих вероятность, не учитывается состояние окружающей среды, в отличие от электромагнитных функций. Одновременно, разница в знаках связана с тем, что электромагнитные компоненты в варианте отображения волны имеют другое взаимодействие при переходе к корпускулярному виду, чем это было при первоначальном представлении объектов из электронных и мюонных нейтрино и антинейтрино. В противном случае говорить о наличии преобразования в новые объекты просто не было бы смысла в силу отсутствия отличий. Соответственно отображение через разные функции Ψ говорит о том, что первоначально используются разные объекты, которые дают при взаимодействии корпускулярные свойства, и есть при этом смена системы наблюдения на противоположную систему наблюдения (в противном случае вид бы не изменялся). Отсюда ротор (разность) во втором уравнении (66) при переходе к уравнениям Дирака также должен менять знак на сумму в силу того, что он уже приводится к корпускулярному виду в системе наблюдения от противоположности.
То есть, при учёте влияния функций в системе уравнений Дирака, мы должны учитывать, что преобразование электромагнитных компонент для получения корпускулярного вида определяет также смену суммы на разность, и наоборот. По сути это означает, что, то, что в одной системе рассматривалось в виде противоположностей, в противоположной системе наблюдения представляется единым целым. Иными словами, в своей системе уравнений Дирак использовал взаимодействие противоположностей с учётом рассмотрения от соответствующих систем наблюдения при переходе от волновых свойств к корпускулярным свойствам с учётом движения и смены знаков. Следовательно, мы при переходе от Ψ функций, характеризующих вероятность, к реальным электромагнитным функциям через векторные потенциалы будем использовать те же условия взаимодействия через аналогичные знаки, что применил Дирак. Понятно, что Дирак не обошёлся без представления объектов в зависимости от системы наблюдения. Соответственно замену волновых функций Ψ на векторные потенциалы можно представить в виде:
| (70) |
При этом волновые функции (Ψ) Луи де Бройля при соответствии уравнению энергии Эйнштейна имеют вид:
![]() , (71)
, (71)
Далее мы можем расписать уравнения на основе векторных потенциалов аналогично системе уравнений Дирака (7) в виде:
| (72) |
Повторим, что здесь мы учитываем, что взаимодействие компонент векторных потенциалов при преобразовании и переходе от волновых свойств к корпускулярным свойствам меняется, так как иное означает отсутствие самого взаимодействия. После взятия производных по волновым функциям аналогичным (71) получим вид:
| (73) |
С учётом выражения одних функций через другие для свободной частицы без влияния внешнего электромагнитного поля получаем:
| (74) |
Далее подставляем одни функции вместо других и сокращаем подобные члены:
| (75) |
С учётом сокращения на общую волновую функцию ![]() , имеем энергию в квадрате для частиц с учётом кинетической энергии от противоположности. Для отражения движения без наличия внешних сил, как положительных (позитрон), так и отрицательных (электрон) частиц, имеем формулу энергии Эйнштейна:
, имеем энергию в квадрате для частиц с учётом кинетической энергии от противоположности. Для отражения движения без наличия внешних сил, как положительных (позитрон), так и отрицательных (электрон) частиц, имеем формулу энергии Эйнштейна:
![]() , (76)
, (76)
Таким образом, мы получили переход от волновых свойств к корпускулярным свойствам на основе векторного потенциала Аэ, а это означает однозначную связь электромагнитных свойств с корпускулярными свойствами. В итоге уравнение (76) соответствует так называемым заряженным элементарным частицам (электрон, позитрон), которые отражают реально движение наипростейших объектов длины или времени, что мы показали в [21, с. 32-56; 22, с. 5-44].
Так как уравнение энергии Эйнштейна действительно не только для таких частиц как электрон и позитрон, а для частиц типа протона и антипротона в виде ![]() [23, с. 237], то необходимо показать, как обеспечивается такое отображение частиц на основе нашей теории. Собственно суть перехода связана с тем, что меняется система наблюдения (это связано с делением на член преобразования Лоренца-Минковского в виде
[23, с. 237], то необходимо показать, как обеспечивается такое отображение частиц на основе нашей теории. Собственно суть перехода связана с тем, что меняется система наблюдения (это связано с делением на член преобразования Лоренца-Минковского в виде ![]() ), что меняет соотношение между потенциальной энергией, связанной с массой, и кинетической энергией в соответствии с СТО и ОТО Эйнштейна. В данном случае для напряжённости магнитного поля в соответствующей системе наблюдения (это определяется делением напряжённости поля на величину
), что меняет соотношение между потенциальной энергией, связанной с массой, и кинетической энергией в соответствии с СТО и ОТО Эйнштейна. В данном случае для напряжённости магнитного поля в соответствующей системе наблюдения (это определяется делением напряжённости поля на величину ![]() ) с преобразованием кинетической энергии в потенциальную энергию имеем:
) с преобразованием кинетической энергии в потенциальную энергию имеем:
| (77) |
Аналогично для напряжённости электрического поля с делением на ![]() имеем:
имеем:
| (78) |
Здесь ![]() . Таким образом вместо
. Таким образом вместо ![]() имеем массу покоя с учётом преобразования кинетической энергии в потенциальную в виде m.
имеем массу покоя с учётом преобразования кинетической энергии в потенциальную в виде m.
При этом надо учитывать, что константы электрической и магнитной проницаемости также имеют зависимость от местоположения в среде распространения, что определяет баланс между частицами и средой в плане синтеза и распада. Соответственно, мы видим, что в отличие от нашей теории, система уравнений Дирака, без учёта состояния среды распространения, не способна описать частицы с разной массой покоя.
Надо отметить, что без замкнутого состояния при равном обмене между противоположностями с учётом наличия констант в виде скорости света и постоянной Планка никакого резонанса в принципе получить было бы невозможно. Кроме того, невозможно было бы получить и корпускулярные свойства, которые образуются за счёт динамики обмена электромагнитными составляющими от первоначальных объектов – электронных и мюонных нейтрино и антинейтрино. Соответственно напомним, что проще математического описания электронных и мюонных нейтрино и антинейтрино ничего быть не может, так как эти объекты отражают динамику изменения и взаимодействия в двух глобальных противоположностях мироздания с условием закона сохранения количества и отсутствие какого-либо дифференциального члена в них из четырёх представленных даёт нарушение равновесия между противоположностями с наличием при этом чудес и отрицанием законов физики.
Из сказанного выше следует, что представление корпускулярных объектов, например, в виде движущихся электрона или протона, зависит от системы наблюдения с учётом преобразований Лоренца – Минковского. Действительно, представить электронное или мюонное нейтрино (антинейтрино) в противоположной системе наблюдения, связанной с первоначальной через скорость света, также в виде того же электронного или мюонного нейтрино (антинейтрино) невозможно, так как это бы означало отсутствие самих противоположностей. Поэтому в противоположности электронные и мюонные нейтрино характеризуют уже корпускулярные объекты (источники поглощения и излучения), и в соответствующей системе наблюдения отражаются в виде объектов длины или времени, что может интерпретироваться в качестве электронов (антипротонов) и позитронов (протонов). Как было показано выше общая формула для отражения движения корпускулярных частиц имеет вид:
![]() , (79)
, (79)
Соответственно динамика изменения энергии частицы при движении должна быть такой, чтобы не было распада частицы. Сам принцип необходимости обмена следует из существования частиц через взаимодействие. Для обмена требуется изменение энергии через силовое воздействие с поглощением одних объектов и излучением других объектов. А это возможно только при выполнении замкнутого движения с учётом равного обмена через поглощение и излучение. В этом случае замкнутое движение частиц описывается уравнением гармонического осциллятора в виде [24, с. 58]:
![]() , (80)
, (80)
Это уравнение для движущейся частицы соответствует уравнению окружности, из которого, как мы показали в [1, с. 6-42; 2, с. 29-63] следуют уравнения (2), на основании которых и получаются корпускулярные свойства частиц. При этом мы учитываем, что объекты излучения одними частицами являются объектами поглощения другими противоположными частицами. То есть, уравнение (79) соответствует взаимодействию противоположных частиц с учётом закона сохранения количества.
Если левая часть уравнения (80) от знака равенства не вызывает сомнения, то кратность энергии в правой части уравнения должно быть обосновано и должно соответствовать практике, так как при выражении объекта в чисто корпускулярном виде это не очевидно. Так как излучение и поглощение связано с изменением энергии, то это не может быть без наличия воздействия сил на объект. Воздействие сил описывается через уравнение с подчинением второму закону Ньютона [25, c. 73]:
| (81) |
На следующем этапе по классической физике берётся некая функция действия ![]() с учётом равенств
с учётом равенств ![]() и
и ![]() . В результате имеем уравнение Гамильтона – Якоби без внешнего поля [26, c. 29]:
. В результате имеем уравнение Гамильтона – Якоби без внешнего поля [26, c. 29]:
![]() , (82)
, (82)
Однако, и в случае системы уравнений Дирака с подчинением уравнению энергии Эйнштейна и в случае (82) мы имеем движущуюся частицу без воздействия внешних сил, но законы взаимодействия разные с отличием по энергии в 2 раза. Это означает неоднозначность и парадокс, так как отсутствует плавный переход. Поэтому надо показать причину такого различия и смысл плавного перехода. Собственно отличие уже видно в том, что в (82) не учитывается замкнутый процесс через взаимодействие противоположностей. Действительно при скорости равной нулю частица уже не имеет энергии и это означает её практическое исчезновение. Иными словами, не учитывается преобразование энергии. Поэтому с этой целью учтём, что уравнение Гамильтона ‒ Якоби при наличии у частицы собственного пространственно-временного искривления в виде потенциального поля приобретает вид:
![]() , (83)
, (83)
В этом случае частица при скорости равной нулю не исчезает и имеет энергию поля (V). Уравнение (83) после дифференцирования и отображения энергии поля от заряда соответствует виду:
![]() , (84)
, (84)
Это уравнение исходя из фотоэффекта, при котором максимальная скорость фотоэлектронов не зависит от интенсивности света, а зависит только от его частоты, было усовершенствовано Эйнштейном [27, с. 36]:
![]() , (85)
, (85)
Иными словами, Эйнштейн предположил, что свет частицей поглощается порциями, какими он по предположению Планка испускается. Собственно, мы здесь ничего нового не придумали, и формула Эйнштейна по (85) переложена от использования энергии выхода (А) электронов из твёрдого или жидкого тела на сам электрон (позитрон) с излучением и поглощением фотонов порциями, как это считал Эйнштейн.
Соответственно теперь надо показать связь формул (80) и (85), и здесь надо учесть преобразования, сделанные самими физиками в квантовой механике для подчинения уравнения Гамильтона-Якоби волновым свойствам. В противном случае о корпускулярно-волновом дуализме на основе противоположностей надо забыть. Поэтому, до системы уравнений Дирака, для описания волновых свойств на основе корпускулярного движения частицы без внешних сил Шредингер предложил вариант уравнения вида [6, с. 30-32]:
![]() , (86)
, (86)
При этом Шредингер учёл, что волновые функции по синусу и косинусу при подстановке в уравнение Гамильтона ‒ Якоби при взятии первой и второй производных не обеспечивают равенство. Поэтому Шредингер был вынужден использовать комплексную волновую функцию Луи де Бройля Ψ по формуле (6) с нормировкой на редуцированную постоянную Планка и умножением первой производной от функции по времени на мнимую единицу. Соответственно, возведение в квадрат первой производной от функции по длине он заменил интуитивно двойным дифференцированием этой функции. В итоге волновой вид комплексной функции позволил получить решение аналогичное тому, какое следовало для уравнения Гамильтона ‒ Якоби от второго закона Ньютона. Совпадение решения для волновой функции Ψ с решением для функции корпускулярной частицы означает возможность сочетания корпускулярных и волновых свойств в одном общем объекте. Но вид уравнений при этом тоже оказался отличающимся. Тогда физики посчитали, что данное уравнение Шредингера должно удовлетворять условию, при котором оно должно в предельном случае переходить в уравнение Гамильтона – Якоби. С этой целью вместо волновой функции ![]() вводят функцию S при помощи соотношения [6, с. 30-32]:
вводят функцию S при помощи соотношения [6, с. 30-32]:
![]() , (87)
, (87)
Ещё раз отметим, что в аргумент экспоненты функции произвольно физиками вводится редуцированная постоянная Планка (![]() ), что соответственно исключает полную замкнутость объекта, так как изменения (дифференцирование или интегрирование) приводят к изменению количества, а значит и уровня иерархии в системе Мироздания. Далее учитывают равенства:
), что соответственно исключает полную замкнутость объекта, так как изменения (дифференцирование или интегрирование) приводят к изменению количества, а значит и уровня иерархии в системе Мироздания. Далее учитывают равенства:
| (88) |
Так как волновая функция Ψ с учётом нормировки (![]() ) входит во все члены лишь множителем, то её можно сократить, тогда получим:
) входит во все члены лишь множителем, то её можно сократить, тогда получим:
![]() , (89)
, (89)
В предельном случае физики полагают, что при величине ![]() , мнимая составляющая пропадает и данное уравнение переходит в уравнение Гамильтона ‒ Якоби. Однако надо напомнить, что по нашей теории, что было показано в [1, с. 6-42]
, мнимая составляющая пропадает и данное уравнение переходит в уравнение Гамильтона ‒ Якоби. Однако надо напомнить, что по нашей теории, что было показано в [1, с. 6-42] ![]() , а это означает, что перехода к уравнению Гамильтона ‒ Якоби просто быть не может, так как нет варианта, при котором
, а это означает, что перехода к уравнению Гамильтона ‒ Якоби просто быть не может, так как нет варианта, при котором ![]() . Приходим к парадоксу математики с Ахиллесом и черепахой с наличием бесконечностей. А с учётом обратно-пропорциональной связи со скоростью света, законов физики, как таковых, просто быть не может. То есть, при
. Приходим к парадоксу математики с Ахиллесом и черепахой с наличием бесконечностей. А с учётом обратно-пропорциональной связи со скоростью света, законов физики, как таковых, просто быть не может. То есть, при ![]() , получается однородность, нарушаются законы физики и, соответственно нет и самих противоположностей. Кроме того, в дальнейшем это уравнение (89) с учётом внешнего потенциального поля используется при методе Вентцеля –Крамерса ‒ Бриллоэна (метод ВКБ) [28, с. 58] для сшивания функций на границе раздела с получением в конечном итоге правила квантования Бора ‒ Зоммерфельда, на основании чего оправдывался туннельный эффект с прохождением через потенциальный энергетический барьер, а также наличие нулевой энергии по соотношению неопределённостей Гейзенберга. При этом исчезновение члена с величиной постоянной Планка исключало доказательство всех остальных преобразований. Парадоксы таких решений мы также подробно рассмотрели в [29, с. 5-27].
, получается однородность, нарушаются законы физики и, соответственно нет и самих противоположностей. Кроме того, в дальнейшем это уравнение (89) с учётом внешнего потенциального поля используется при методе Вентцеля –Крамерса ‒ Бриллоэна (метод ВКБ) [28, с. 58] для сшивания функций на границе раздела с получением в конечном итоге правила квантования Бора ‒ Зоммерфельда, на основании чего оправдывался туннельный эффект с прохождением через потенциальный энергетический барьер, а также наличие нулевой энергии по соотношению неопределённостей Гейзенберга. При этом исчезновение члена с величиной постоянной Планка исключало доказательство всех остальных преобразований. Парадоксы таких решений мы также подробно рассмотрели в [29, с. 5-27].
Таким образом, предложенный физиками переход к уравнению Гамильтона-Якоби не соответствовал истине. Чтобы понять какую роль играет изменение аргумента функции в (87-89), покажем связь уравнения Шредингера вида (86) с уравнением гармонического осциллятора, как это предложено в квантовой механике и считаем, что сила притяжения потенциального поля равна силе отталкивания. При этом напомним, что гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы F=‒kx [30, с. 90]. Потенциальная энергия такой частицы имеет вид:
![]() , (90)
, (90)
Собственная частота классического гармонического осциллятора при массе частицы m0 равна:
![]() , (91)
, (91)
Далее получим формулу для потенциальной энергии частицы в виде:
![]() , (92)
, (92)
После взятия производных в (86) мы имеем уравнение:
![]() , (93)
, (93)
Отсюда с учётом равенства поглощения и излучения для наличия соблюдения закона сохранения количества между противоположностями в стабильном объекте при Е=hf получаем формулу гармонического осциллятора.
Собственно, совпадение получено благодаря использованию квазиупругой силы F=‒kx, которая не имеет никакого обоснования для описания свойств самой частицы. Это чистая подгонка под результат. Кроме того, соответствие связано и с тем, что в качестве волновой функции используется функция Луи де Бройля, вид которой не меняется при дифференцировании или интегрировании, что говорит об отсутствии распада частицы. В результате операция двойного дифференцирования даёт такой же результат, как и возведение в квадрат. Однако двойное дифференцирование означает возврат в ту же противоположность, но с противодействием объекту, в то время как возведение в квадрат характеризует одну и ту же величину (объект). То есть, Шредингер не учёл, что основой для совмещения корпускулярных и волновых свойств является закон действия и противодействия для противоположностей. В этом случае должно соблюдаться равенство:
![]() , (94)
, (94)
В этом равенстве учитывается, что равенство изменений соблюдается с учётом дифференцирования по соответствующим аргументам. При этом при изменении нет разницы на коэффициент равный двойке, что бы нарушило количественное равенство. Собственно, это уравнение определяет закон сохранения частицы на уровне силы действия и противодействия на основе изменений в противоположностях объекта. Соответственно это равенство определяет и вид волновой функции Луи де Бройля вида ![]() :
:
![]() , (95)
, (95)
Здесь коэффициент в аргументе равный двойке учитывает условие перехода формул Эйлера к волновым функциям и пространственно-временному искривлению в виде:
| (96) |
Иными словами уравнение Гамильтона-Якоби без наличия потенциального поля отображает не полностью замкнутую систему. Действительно если исходить из замкнутой системы по циклу Карно, то энергия замкнутой системы определяется площадью вида ![]() , соответственно такое изменение энергии определяется движением по окружности
, соответственно такое изменение энергии определяется движением по окружности ![]() . Действительно, движение по окружности в любом случае связано с изменением направления движения, а значит и с изменением энергии. При этом мы видим, что есть разница на коэффициент равный двойке. Это означает, что движение по окружности определяет изменение энергии в одном направлении, а для соблюдения закона сохранения самого объекта требуется изменение энергии и в обратном направлении. В аргументе функции (95) коэффициент равный постоянной Планка (h=m0) означает, что переход в противоположность означает также смену уровня в иерархии Мироздания на шаг дискретизации. В противном случае был бы возможен вечный двигатель или полностью замкнутый объект помимо всего Мироздания.
. Действительно, движение по окружности в любом случае связано с изменением направления движения, а значит и с изменением энергии. При этом мы видим, что есть разница на коэффициент равный двойке. Это означает, что движение по окружности определяет изменение энергии в одном направлении, а для соблюдения закона сохранения самого объекта требуется изменение энергии и в обратном направлении. В аргументе функции (95) коэффициент равный постоянной Планка (h=m0) означает, что переход в противоположность означает также смену уровня в иерархии Мироздания на шаг дискретизации. В противном случае был бы возможен вечный двигатель или полностью замкнутый объект помимо всего Мироздания.
Далее мы учитываем, что Дирак любое дифференцирование ещё до нас связал с дополнительным умножением на мнимую единицу по формулам в (5). Мы лишь в теории Мироздания [1, с. 6-42] дали этому логическое обоснование. Отсюда в частном случае получается решение:
| (97) |
Здесь сокращением на ![]() мы исключаем условие перехода на новый уровень иерархии в системе Мироздания. Это можно сделать при условии сохранения самого объекта, так как имеется равенство между излучением и поглощением. Собственно такое сокращение – это тоже не наша выдумка, а было применено самими физиками, что было показано выше в (89), где было сделано сокращение нормировки на член
мы исключаем условие перехода на новый уровень иерархии в системе Мироздания. Это можно сделать при условии сохранения самого объекта, так как имеется равенство между излучением и поглощением. Собственно такое сокращение – это тоже не наша выдумка, а было применено самими физиками, что было показано выше в (89), где было сделано сокращение нормировки на член ![]() . Надо отметить, что в [21, с. 32-56] мы дали логическое объяснение коэффициенту 1/(2h) как величине связи между механическим движением и магнитным моментом (это и отражает необходимость корпускулярно-волнового дуализма любого объекта), и значение ½ связано с тем, что учитывается только одна – магнитная составляющая при связи противоположностей через скорость света. Следует отметить, что величина 1/(2m0) гиромагнитного отношения по нашей теории играет основную роль в вычислении аномальных магнитных моментов.
. Надо отметить, что в [21, с. 32-56] мы дали логическое объяснение коэффициенту 1/(2h) как величине связи между механическим движением и магнитным моментом (это и отражает необходимость корпускулярно-волнового дуализма любого объекта), и значение ½ связано с тем, что учитывается только одна – магнитная составляющая при связи противоположностей через скорость света. Следует отметить, что величина 1/(2m0) гиромагнитного отношения по нашей теории играет основную роль в вычислении аномальных магнитных моментов.
Соответственно, теперь надо показать, есть ли возможность перехода от уравнения сил (94) с волновой функцией Ψ по (95) к корпускулярному движению частицы, как это получилось для системы уравнений Дирака. Иными словами, мы пытаемся доказать, что уравнение Гамильтона ‒ Якоби без внешнего потенциального поля не полностью описывает частицу исходя из корпускулярно-волнового дуализма, то есть замкнутой системы. Отсюда, теперь надо разобраться, что, собственно, даёт учёт взаимодействия корпускулярных и волновых свойств, при законе сохранения количества за счёт перехода от возведения в квадрат первой производной функции от длины в уравнении Гамильтона ‒ Якоби к двойному дифференцированию по длине этой же функции. Если волновая функция Ψ имеет вид (95), то мы имеем уравнение Гамильтона ‒ Якоби (55). Однако, если исходить из функции (87), то здесь учитывается и изменение самого аргумента, а это уже вариант взаимодействия противоположностей. То есть уравнение Шредингера может рассматривать процесс во взаимосвязи противоположностей, а не в варианте наличия одной противоположности по волновой функции Ψ с решением (95). При этом должно соблюдаться условие закона сохранения количества, так как объект не исчезает в результате движения. В противном случае объекта без взаимодействия противоположностей в принципе быть не может.
В нашем случае функция S(r,t) отражает изменяемую величину всего аргумента как единого целого (тем самым исключаем переход на другой уровень иерархии в Мироздании в силу замкнутости объекта с его неизменностью во времени). Поэтому, мы будем иметь вид без нормировочного коэффициента, дающего переход на другой уровень иерархии, в виде величины постоянной Планка:
![]() , (98)
, (98)
В итоге с учётом правила дифференцирования с умножением на мнимую единицу, предложенного в (5) Дираком, и доказанного в нашей теории [1, с. 6-42], получаем равенства:
| (99) |
С учётом (98) и поскольку волновая функция Ψ в результате данного преобразования должна входить во все члены лишь множителем, мы можем её сократить. В итоге получаем:
![]() , (100)
, (100)
При учёте волновой функции Ψ вида (98) в одной системе наблюдения и волновой функции от аргумента ![]() в противоположной системе наблюдения, с учётом того, что дифференцирование соответствует условиям Дирака вида (5), мы имеем уравнение:
в противоположной системе наблюдения, с учётом того, что дифференцирование соответствует условиям Дирака вида (5), мы имеем уравнение:
| (101) |
В данном случае общая энергия объекта характеризуется двумя равными составляющими, что, собственно, и было обозначено в формуле гармонического осциллятора (80), если учесть, что ![]() . Иными словами, мы имеем связь уравнения гармонического осциллятора (80) с полным уравнением Гамильтона ‒ Якоби на основе корпускулярно-волнового дуализма с учётом кинетической и потенциальной энергии, на основе равенства сил между противоположностями за счёт изменения аргумента S при функции Ψ.
. Иными словами, мы имеем связь уравнения гармонического осциллятора (80) с полным уравнением Гамильтона ‒ Якоби на основе корпускулярно-волнового дуализма с учётом кинетической и потенциальной энергии, на основе равенства сил между противоположностями за счёт изменения аргумента S при функции Ψ.
То есть при учёте корпускулярно-волнового дуализма движущегося объекта полное уравнение Гамильтона – Якоби соответствует уравнению гармонического осциллятора, которое также соответствует уравнению окружности. А выше мы также показали, как уравнение окружности переходит в уравнение энергии Эйнштейна, из которого выводится система уравнений Дирака. Тем самым мы разрешили парадокс неоднозначности, который был между уравнением энергии Эйнштейна и уравнением Гамильтона – Якоби исходя из наличия корпускулярно-волнового дуализма. Соответственно, если уравнение Гамильтона ‒ Якоби (83) описывает корпускулярное движение частицы в некотором внешнем потенциальном поле, то уравнение (100) описывает условие сохранения самой частицы как корпускулярно-волнового объекта на основе равенства силы действия и противодействия с учётом кинетической и потенциальной энергии этого объекта. В этом случае замкнутой системе объекта при взаимодействии противоположностей обеспечивается резонанс при поглощении и излучении с наличием дискретности в постоянную Планка, что было предложено Эйнштейном и Планком исходя из фотоэффекта. Собственно, сама дискретность связано именно с наличием волновых свойств, так как резонанс обеспечивается за счёт кратности по длине волны. Так как объект при отсутствии распада взаимодействует с внешней средой через излучение и поглощение, то на основании этого и было вычислено отношение массы протона к массе электрона с учётом пика резонанса по формуле Планка в силу отсутствия изменений в законе сохранения количества между объектом и средой в [2, с. 29-63] в виде:
![]() , (102)
, (102)
Уравнение гармонического осциллятора (80), исходя из соответствия уравнению окружности, описывает орбитальное движение элементарной частицы (электрон), характеризующей одну противоположность, относительно противоположной частицы с большей массой покоя (протон). Соответственно в этом случае нас интересует вопрос: «Каким образом можно вычислить отношение радиуса орбиты электрона к радиусу электрона?» Собственно необходимость этого следует из того, что фактически радиус вращения непосредственно связан с кинетической энергией частицы, которая в противоположности определяет массу покоя. Кроме того, это необходимо сделать потому, что вычисление боровских орбит с использованием системы измерения СИ или СГС только с применением количественных оценок на основе констант по нашей теории Мироздания даёт парадокс, при котором просто не может быть динамики изменения и обмена, а значит изменение орбит может происходить только через чудеса. Отметим, что для вычисления радиуса орбиты Бор, на основе уравнения гармонического осциллятора (80), получил соотношения связи радиуса и импульса в виде:
| (103) |
По сути, при n=1 мы имеем разницу с (36) на величину ![]() , что связано с тем, что в (36) мы длину окружности связали с частотой через период повторения замкнутого цикла по времени. То есть учитывали преобразование времени в длину в зависимости от системы наблюдения и изменения происходят по мере движения по пути следования, то есть длине окружности. В (103) изначально рассматривается замкнутый цикл в противоположной системе наблюдения с замкнутым циклом по энергии с использованием радиуса. Исходя из (103) Бор сделал замену скорости на радиус и получил:
, что связано с тем, что в (36) мы длину окружности связали с частотой через период повторения замкнутого цикла по времени. То есть учитывали преобразование времени в длину в зависимости от системы наблюдения и изменения происходят по мере движения по пути следования, то есть длине окружности. В (103) изначально рассматривается замкнутый цикл в противоположной системе наблюдения с замкнутым циклом по энергии с использованием радиуса. Исходя из (103) Бор сделал замену скорости на радиус и получил:
![]() , (104)
, (104)
Понятно, что такая произвольная замена с точки зрения классической физики не имело никакого обоснования, так как исчезало понятие кинетической энергии, связанной со скоростью движения объекта, и она превращалась в длину в виде радиуса. Но с точки зрения нашей теории, в которой скорость и масса (длина) меняются местами в зависимости от системы наблюдения из противоположности, это имеет смысл. Иными словами, Бор уже до нас интуитивно ввёл представление объекта в зависимости, от системы наблюдения, поменяв скорость на длину. Причём мы видим, что при переходе от отображения объектов в одной системе наблюдения (кинетическая энергия), к отображению объектов в другой противоположной системе наблюдения (потенциальная энергия), у нас идёт пересчёт с возведением величины длины в квадрате, и это тоже было сделано до нас Бором. Исходя из формулы (104), можно перейти к уравнению только баланса противодействующих сил с учётом значения энергии Е как константы, не зависящей от радиуса при минимальной энергии, продифференцировав уравнение (104) по радиусу. В итоге для радиуса первой боровской орбиты получим [31, с. 71]:
| (105) |
Этот же результат получается, если использовать уравнение вида:
![]() , (106)
, (106)
Собственно, по (106) при v=c мы имеем формулу для размеров электрона. После преобразований имеем вид:
| (107) |
Казалось бы, противоречий в логике нет (с учётом нашей теории). Однако, отсюда следует парадокс, допущенный Бором в том, что своим постулатом по дискретным орбитам он исключил излучение при движении электрона на дискретных орбитах, в то время как уравнение гармонического осциллятора основано на излучении, в виде значения ![]() , и именно это соотношение используется в (102) для получения боровской орбиты. Отметим, что на основе констант в (107) невозможно определить также механизм излучения (поглощения), так как нет изменяемых величин.
, и именно это соотношение используется в (102) для получения боровской орбиты. Отметим, что на основе констант в (107) невозможно определить также механизм излучения (поглощения), так как нет изменяемых величин.
При этом вычисление первой боровской орбиты на основании формулы, применённой Бором (107), даёт по нашей теории с учётом и теории Дирака ![]() значение:
значение: ![]() . Иными словами, приходим к тому, что первая боровская орбита меньше постоянной Планка. Кроме того, параметры среды распространения также не входят в формулу расчёта, то есть мы имеем пространство и время по геометрии Эвклида, а это отрицание СТО и ОТО Эйнштейна.
. Иными словами, приходим к тому, что первая боровская орбита меньше постоянной Планка. Кроме того, параметры среды распространения также не входят в формулу расчёта, то есть мы имеем пространство и время по геометрии Эвклида, а это отрицание СТО и ОТО Эйнштейна.
Поэтому будем определять значение первой боровской орбиты также на основе противодействующих друг другу реальных сил, но на основе электрической и магнитной силы, и без так называемой центробежной силы. Суть такой замены связана с тем, что по СТО и ОТО Эйнштейна представление электрических и магнитных сил относительно, в то время как центробежная сила никак не вписывается в этот электромагнитный континуум и её нет при описании корпускулярных свойств частицы по системе уравнений Дирака. С этой целью необходимо вспомнить формулу отношения электрической силы (сила Кулона) к магнитной силе (сила Лоренца) при взаимодействии одинаковых точечных зарядов (e) в виде [32, с. 119]:
![]() , (108)
, (108)
Такое отношение для вращающегося электрона вокруг протона связано с тем, что мы имеем симметрию в противоположностях, которая обусловлена законом сохранения количества в этих противоположностях. По сути, это отношение напряжённостей электрического и магнитного поля. По (108) отношение электрической силы (сила Кулона) к магнитной силе (сила Лоренца) определяется значением скорости в квадрате. При этом движение рассматривается в противоположности, связанной с тем, что в ОТО используется абсолютная система отсчёта, и для определения пространственно-временного искривления используется проекции скорости на время. Здесь значение соотношения сил (напряжённостей полей), эквивалентно соотношению в (108), и должно пересчитываться, в противоположной системе наблюдения, в соотношение радиуса первой боровской орбиты к радиусу электрона. В противном случае мы не будем наблюдать общего пространственно-временного электромагнитного континуума, если при смене системы наблюдения нет изменений в представлении. Подчеркнём, что такую замену придумали не мы, а Бор. Соответственно, мы должны учесть переход от волнового вида (кинетическая энергия) к пространственно-временному искривлению (потенциальная энергия) с учётом двойного дифференцирования от аргумента волновой функции. В этом случае длина в системе наблюдения от напряжённостей полей по аргументу при преобразовании будет в квадрате. Собственно, такую же зависимость мы показали в [2, с. 29-63] при определении мощности излучения от частоты на основе классической электродинамики в виде:
| (109) |
Фактически это означает, что среда распространения в одной противоположности, представленная через аргумент волновой функции связана в квадратичной зависимости со средой распространения в другой противоположности на основе решения волнового уравнения, которое характеризует преобразование. Отсюда, учитывая разницу на ![]() по формулам (36), и (103) мы от отношения сил от напряжённостей полей переходим к отношению радиуса орбиты движения электрона к радиусу электрона, с учётом
по формулам (36), и (103) мы от отношения сил от напряжённостей полей переходим к отношению радиуса орбиты движения электрона к радиусу электрона, с учётом ![]() :
:
| (110) |
Кроме того, мы считаем, что в отличие от системы СИ у нас отношение, как и в случае вычисления отношения масс протона и электрона, определяется величиной ![]() . При этом устойчивое состояние протона достигается за счёт максимума по спектру излучения, которое отличается от среднего значения в соответствии с формулой Планка по термодинамическому равновесию на коэффициент 4,965. Следовательно, отношение радиуса первой боровской орбиты rбо к радиусу электрона rэ будет определяться в виде:
. При этом устойчивое состояние протона достигается за счёт максимума по спектру излучения, которое отличается от среднего значения в соответствии с формулой Планка по термодинамическому равновесию на коэффициент 4,965. Следовательно, отношение радиуса первой боровской орбиты rбо к радиусу электрона rэ будет определяться в виде:
![]() , (111)
, (111)
Иными словами, мы вычислили параметр орбиты движения электрона вокруг протона также исходя из параметров окружающей среды распространения. При этом мы установили квадратичную зависимость, при которой, в одной противоположности, при определении соотношения массы протона к массе электрона, за счёт пространственно-временного искривления, использовалось соотношение ![]() . В другой противоположности пространственно-временное искривление определялось величиной
. В другой противоположности пространственно-временное искривление определялось величиной ![]() , и эти соотношения следовали из классической электродинамики.
, и эти соотношения следовали из классической электродинамики.
Это как раз и означает, что объекты в противоположностях имеют разное представление. В одной противоположности объекты описываются как протон и электрон, а в другой противоположности это уже движущийся по орбите электрон вокруг протона.
Собственно открытие, сделанное в нашей теории, касается того, что мы вычислили устойчивое резонансное состояние электрона на орбите, а также наличие разницы масс протона и электрона, благодаря динамике взаимодействия противоположностей через излучение и поглощение с учётом пика излучения (резонанса) по формуле Планка, которая определяет термодинамическое равновесие. При этом благодаря представлению уравнения Гамильтона-Якоби через равенство противодействующих сил с получением замкнутости аналогичной уравнению гармонического осциллятора нашлось обоснование дискретному излучению электрона (позитрона) пропорционально постоянной Планка, которая определяет замкнутость объекта по окружности на основании (36), что интуитивно было предложено Эйнштейном и Планком. В классике квантовой механики по (107) также проведены расчёты отношения радиуса первой боровской орбиты к радиусу электрона с учётом единиц измерения, однако нет вычисления массы протона к массе электрона. При этом в системе СИ радиус электрона равен величине:
![]() , (112)
, (112)
Радиус первой боровской орбиты по Бору равен:
![]() , (113)
, (113)
В этом случае имеем:
![]() , (114)
, (114)
Какие при этом были использованы подгонки под результат, мы показали в [33, с. 12-32]. Иными словами, в классической квантовой механике получается практически аналогичный результат. Но, следует отметить, что этот результат, был получен без учёта параметров среды распространения, таких как константы электрической и магнитной проницаемости с учётом формулы Планка (в нашей теории это изменяемые параметры и связаны с кинетической энергией в противоположности на основе термодинамического равновесия). Это говорит об отсутствии возможности как-то влиять на среду распространения, следовательно, исключается применение среды как переносчика взаимодействия. То есть, константы электрической и магнитной проницаемости не являются по классике физики изменяемыми параметрами, а значит, нет и динамики взаимодействия через обмен. При этом значение заряда q = е = 1,602176487∙10‒19 Кл противоречит уравнению энергии Эйнштейна, где под заряд нет энергии и ![]() . Следовательно, вычисление первой боровской орбиты на основе системы измерения СИ дало хорошие результаты в результате подгонки за счёт выбора соответствующих единиц измерения. В системе СГС константы электрической и магнитной проницаемости вообще равны единице.
. Следовательно, вычисление первой боровской орбиты на основе системы измерения СИ дало хорошие результаты в результате подгонки за счёт выбора соответствующих единиц измерения. В системе СГС константы электрической и магнитной проницаемости вообще равны единице.
Иными словами, среда распространения в системах единиц измерения, утверждёнными физиками, ‒ это некая «однородная» субстанция не подчиняющаяся СТО и ОТО Эйнштейна. Кроме того, введённые искусственно системы измерения СИ и СГС привели в итоге к обоснованию чёрных дыр из-за радиуса Шварцшильда, кварков и глюонов из-за дробности электрических зарядов, которые выражают энергию взаимодействия.
Однако если представить в квантовой механике выражение радиусов через величину постоянной тонкой структуры, то получим:
| (115) |
Отличие от (112) и (113) в том, что мы перешли на представление радиусов через постоянную тонкой структуры (![]() ), но, сами величины количественно не меняются. В результате отношение даёт значение
), но, сами величины количественно не меняются. В результате отношение даёт значение ![]() . Отсюда можно прийти и к нашей системе измерения при
. Отсюда можно прийти и к нашей системе измерения при ![]() , используя соответствующие преобразования:
, используя соответствующие преобразования:
| (116) |
Следовательно, если считать, что ![]() , с учётом пересчёта от постоянной тонкой структуры (
, с учётом пересчёта от постоянной тонкой структуры (![]() ), то мы получим зависимость от среды распространения и в квантовой механике (с учётом смены системы измерения) в соответствии с нашими уравнениями (65 и 66), когда константы электрической и магнитной проницаемости выступают как характеристики длин пространственно-временного искривления с учётом движения в противоположности. Разница лишь в том, что наша система измерения по уравнению (111) учитывает ещё и замкнутый резонанс противоположностей через коэффициент 4,965 по формуле Планка, что, собственно, и определяет наличие спектральных составляющих. Понятно, что необходимый резонанс в виде пика излучения не получить в квантовой механике даже при преобразованиях в (116), так как мы имеем дело с константами. Кроме того, благодаря квадратичной зависимости связи значений длин в противоположностях мы имеем в соответствии с формулами (103) и (110) делитель на величину
), то мы получим зависимость от среды распространения и в квантовой механике (с учётом смены системы измерения) в соответствии с нашими уравнениями (65 и 66), когда константы электрической и магнитной проницаемости выступают как характеристики длин пространственно-временного искривления с учётом движения в противоположности. Разница лишь в том, что наша система измерения по уравнению (111) учитывает ещё и замкнутый резонанс противоположностей через коэффициент 4,965 по формуле Планка, что, собственно, и определяет наличие спектральных составляющих. Понятно, что необходимый резонанс в виде пика излучения не получить в квантовой механике даже при преобразованиях в (116), так как мы имеем дело с константами. Кроме того, благодаря квадратичной зависимости связи значений длин в противоположностях мы имеем в соответствии с формулами (103) и (110) делитель на величину ![]() , что, собственно, было выведено Бором. Повторим, что из формулы (113) нельзя судить ни о каком резонансе с наличием дискретности орбиты, ни о физике образования радиуса орбиты, так как все входящие величины, в том числе и значения зарядов, являются константами. Для резонанса нужна замкнутая динамика обмена, а её как раз при константах быть не может. Поэтому мы совместили так называемые константы электрической и магнитной проницаемости, которые отражают движение в противоположности, с постоянной тонкой структуры. Тем самым дробное значение зарядов, которое отражает силу взаимодействия, также стало связано с движением в противоположности, но при этом нет принципа образования резонанса.
, что, собственно, было выведено Бором. Повторим, что из формулы (113) нельзя судить ни о каком резонансе с наличием дискретности орбиты, ни о физике образования радиуса орбиты, так как все входящие величины, в том числе и значения зарядов, являются константами. Для резонанса нужна замкнутая динамика обмена, а её как раз при константах быть не может. Поэтому мы совместили так называемые константы электрической и магнитной проницаемости, которые отражают движение в противоположности, с постоянной тонкой структуры. Тем самым дробное значение зарядов, которое отражает силу взаимодействия, также стало связано с движением в противоположности, но при этом нет принципа образования резонанса.
Отсюда становится понятным, почему подгонка под результат, сделанная Бором, дало хорошее совпадение с практикой. Таким образом, мы получили подтверждение практических параметров атома водорода с логическим их обоснованием на основе нашей теории, которая следует из уже известных формул физики. Понятно, что при этом оказалось необходимым представить константы электрической и магнитной проницаемости с их подчинением СТО и ОТО Эйнштейна.
Соответственно теперь необходимо показать связь с практическими результатами, связанными с излучением спектральных составляющих атома водорода. Учитывая замкнутый обмен между противоположностями с наличием максимума излучения по формуле Планка и вычисленными нами значениями отношения массы протона к массе электрона и соотношения радиуса первой боровской орбиты к радиусу электрона, следует предположить, что следующие значения орбит будут кратны к радиусу первой боровской орбиты, так как резонанс с условием закона сохранения количества связан с кратностью по длине волны. В квантовой механике [24, с. 58] для доказательства этого использовалось уравнение (101). Далее, исходя из формулы (106) в квантовой механике рассматривали соотношение:
![]() , (117)
, (117)
По сути, здесь величина кинетической энергии была приравнена к величине потенциальной энергии. Это соотношение было подставлено в (101) с получением формулы:
![]() , (118)
, (118)
Такая подстановка фактически означает условие превращения кинетической энергии частицы в эквивалент потенциальной энергии в противоположной системе наблюдения. Как будет показано несколько ниже это тоже не наша выдумка. На следующем шаге сделана подстановка в значение энергии радиуса первой орбиты по формуле (113) с получением «отрицательной» энергии:
![]() , (119)
, (119)
Для определения энергетических уровней используется подстановка (107) при значениях n=1,2,3,….
| (120) |
В этом случае получается, что значение энергии взаимодействия от кулоновских сил убывает кратно величине n2, так как при этом возрастает радиус орбит движения электрона вокруг протона. Следует отметить, что с учётом нашей теории коэффициент равный двойке учитывает только одну энергетическую составляющую объекта в виде напряжённости электрического поля. Отсюда энергия взаимодействия имеет значение половины от общей энергии объекта. Реальный объект всегда имеет две энергетические составляющие от напряжённостей электрического и магнитного поля. Соответственно резонанс определяется в виде величины кратной радиусу первой боровской орбиты, так как мы не имеем изменения массы протона в динамике взаимодействия противоположностей при изменении радиуса орбиты электрона. Это связано с тем, что константы электрической и магнитной проницаемости определяются исходя из общей кинетической энергии в противоположности, которая не меняется с изменением радиуса электрона в нашей системе наблюдения. Отсюда мы имеем резонанс кратный радиусу первой боровской орбите. С учётом нашей теории значение ![]() меняется на величину в выражении (111), и мы имеем совпадение практических результатов. Далее считается, что при переходе атома водорода из состояния n в состояние m излучается фотон, что даёт спектр атома водорода:
меняется на величину в выражении (111), и мы имеем совпадение практических результатов. Далее считается, что при переходе атома водорода из состояния n в состояние m излучается фотон, что даёт спектр атома водорода:
| (121) |
В этом случае получается, что чем больше значение орбиты по радиусу со значением ![]() , тем энергия взаимодействия на основе кулоновских сил ближе к нулю (рис.).
, тем энергия взаимодействия на основе кулоновских сил ближе к нулю (рис.).
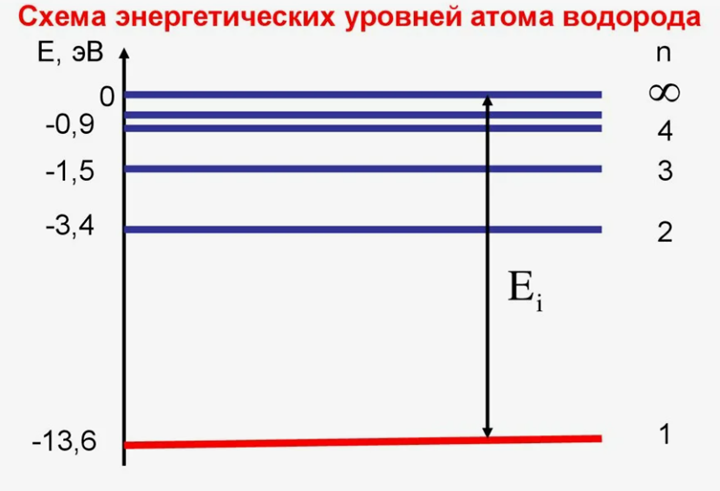
Рис. Схема энергетических уровней атома водорода
То есть сила взаимодействия ослабевает с убыванием потенциальной энергии взаимодействия. Здесь переход к кинетической энергии частицы на орбите связан с разностью от значений потенциальной энергии в зависимости от радиуса. При этом постоянная Ридберга с учётом постоянной тонкой структуры имела величину:
![]() , (122)
, (122)
Величина постоянной Ридберга по теории совпала с величиной, полученной на практике. Однако только наша теория позволила обосновать логику резонансных явлений с кратностью постоянной Ридберга исходя из взаимодействия между противоположностями через обмен.
Представление кинетической энергии в одной противоположности в виде потенциальной энергии в другой противоположности было интуитивно продолжено и в квантовой механике на основании метода ВКБ и подробно разобрано нами в [34, с. 6-37].
Таким образом, мы обосновали переход не только к корпускулярному представлению частиц, но и показали каким образом получаются дискретные орбиты с соответствием их значений практическим результатам.
.png&w=384&q=75)
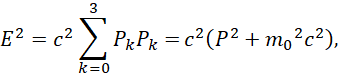
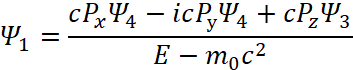 ;
;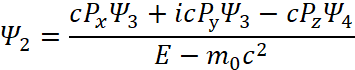 ;
;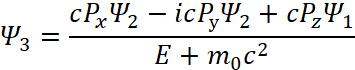 ;
;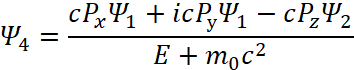 ;
;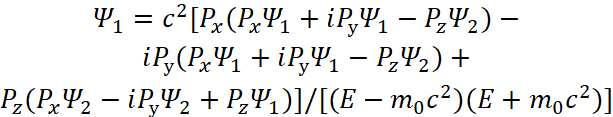 ;
;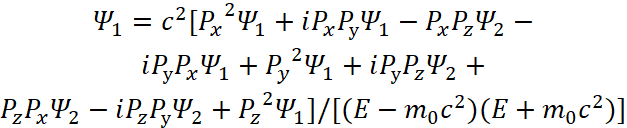 ,
,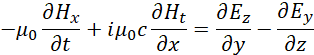 ;
;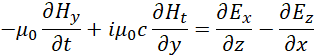 ;
;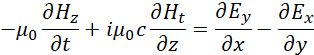 ;
;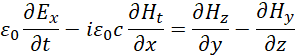 ;
;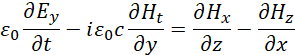 ;
;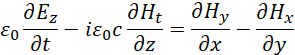 ,
,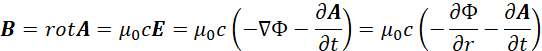 ;
;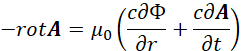 ,
,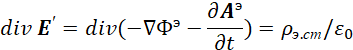 ;
;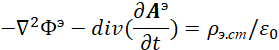 ,
,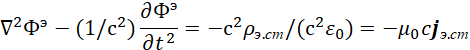 ;
;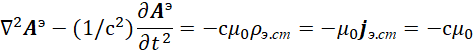 ,
,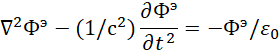 ;
;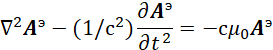 ,
,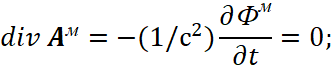
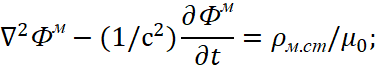
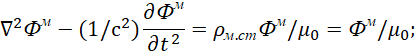
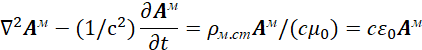
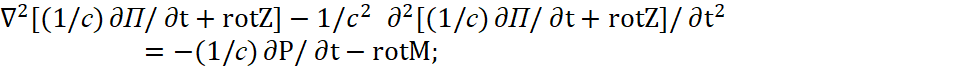
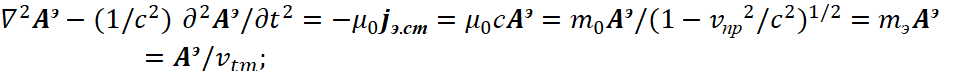
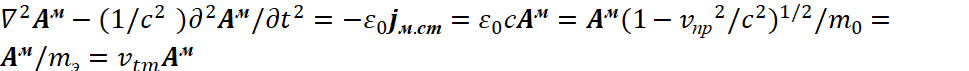 ,
,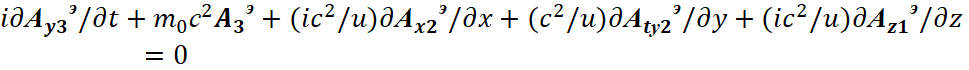
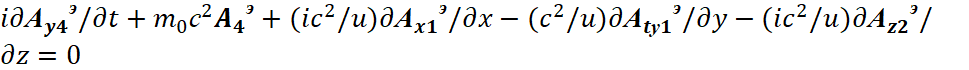 ,
,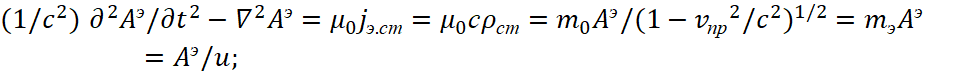
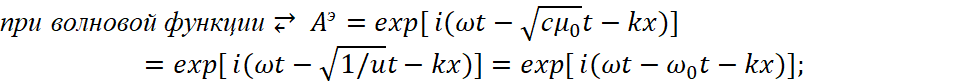
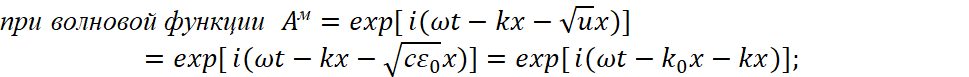
.png&w=640&q=75)