Уравнения в квад-графах и отображения Янга-Бакстера

Уравнения в квад-графax и интегрируемость.

Определим функцию от целочисленного аргумента , где . Преобразование называется сдвигом функции на 1.

Пример разностного уравнения:

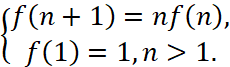, (1)

Это рекуррентное уравнение – основное свойство гамма-функции.

Решение

подставим в исходное уравнение: .

Аналогичным образом можно выразить и так далее до 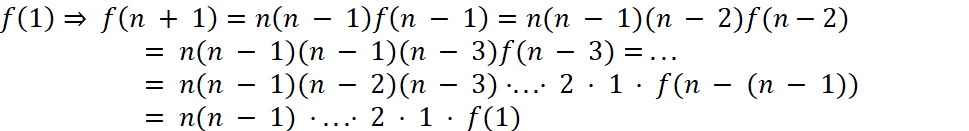. По условию , значит  .

Аналогично функция двух переменных: , где .

Примеры: , , , .

На рисунке представление этих функций на решётке :

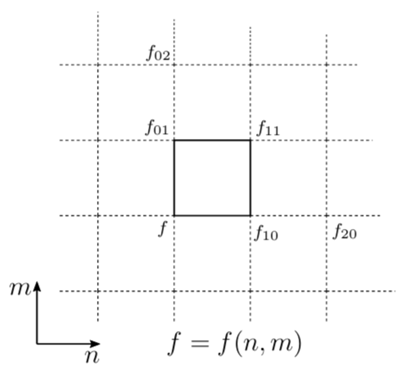
Рис. 1

Пусть нелинейная полиномиальная функция линейна по каждому аргументу (т. е. нет элементов вида ), где a,b ∈ C параметры. Элемент называется полем в вершинах квад-графа.

Определение 1.1. Уравнением в квад-графах называется уравнение вида:

, (2)

Линейность функции Q по каждому аргументу позволяет решать уравнение (2) единственно относительно каждого аргумента.

На следующем рисунке показано, что уравнение (2) определяет четыре вершины одного квадрата. И если известны то через них можно выразить .

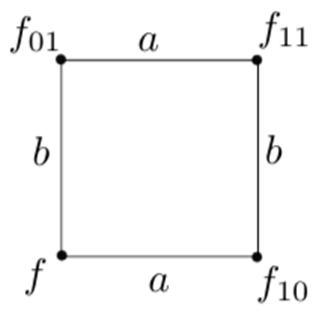
Рис. 2. Уравнение в квад-графах

Вообще, не известно общих прямых методов решения нелинейных разностных уравнений (4.1). Будем говорить, что уравнение (2) – интегрируемое, если можно непрямыми методами построить для него решение. Общего определения интегрируемости нет, но далее будут некоторые «рабочие» определения.

Первое понятие интегрируемости: нелинейное уравнение (2) можно записать как условие совместимости линейной системы.

Есть пара матриц:

и . Рассмотрим следующую линейную систему:

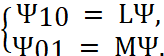, (3)

– вспомогательная матрица. Цель: назначить линейную систему (2) нелинейному уравнению (4.1).

Система (4.2) переопределённая, поэтому надо, чтобы уравнения этой системы были совместными. Сдвигаем первое уравнение на 01, а второе на 10, получится:

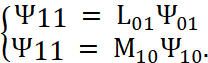, (4)

Далее можно подставить :

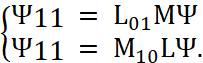, (5)

Эта система уравнений совместна (имеет решение), если

, (6)

Пара матриц L и M называется парой Лакса, а само уравнение называется уравнением Лакса. Для уравнений (2), которые имеют пару Лакса, есть методы построения их решений. Поэтому, имеет смысл дать следующее определение.

Определение 1.2. Уравнение (2) является интегрируемым, если его можно эквивалентно переписать как условие совместимости системы – уравнение Лакса (6). И тогда, (6) называется представлением Лакса уравнения (2).

Кроме того, есть более сильное определение интегрируемости, в частности следующее.

Определение 1.3. Уравнение (2) интегрируемо, если оно обладает свойством 3D-совместности.

Замечание 4.1.4. Если уравнение обладает свойством 3D-совместности, то возможно алгоритмическое построение решения для него.

Пример, дискретное потенциальное уравнение Кортевега–де Фриза (КдФ):

, (7)

Свойство трехмерной совместности vs уравнения Янга–Бакстера.

Уравнение (4.1) в квад-графах обладает свойством 3D-совместности, если каждой грани куба можно сопоставить однотипные уравнения с разными аргументами таким образом, что система из этих уравнений будет совместной.

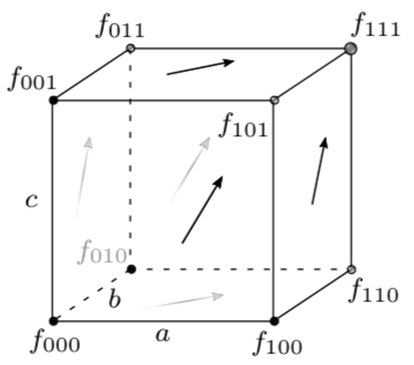
Рис. 3. Свойство 3D-совместности для уравнения в квад-графах

Пример свойства 3D-совместности для уравнения КдФ:

, (8)

Зная , можно выразить остальные .

В каждой грани, где известно три аргумента, найдём четвёртый. Уравнение для нижней грани:

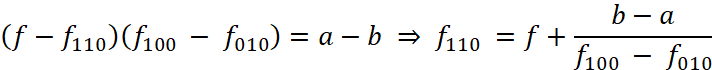, (9)

Уравнение для передней грани:

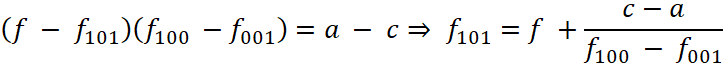, (10)

Уравнение для левой грани:

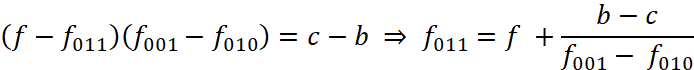, (11)

Далее сдвигаем (4.6) на 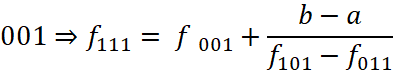– первый способ;

 (4.7) на 010 ⇒ 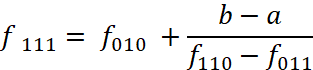– второй способ;

(4.8) на 100 ⇒ 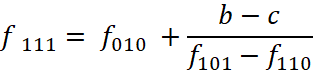– третий способ.

Получилось три разных способа найти , если все они равны, то исходное уравнение обладает свойством 3D-совместности. Для проверки равенства надо все способы выразить только с помощью . Следовательно, в первый способ вместо подставляем правую часть (4.7), а вместо праву часть (4.8). Аналогичным образом преобразуем второй и третий способ. Затем, после упрощения получится одинаковое выражение для всех трёх способов:

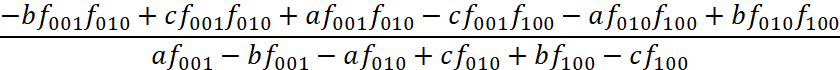, (12)

Таким образом, уравнение (11) обладает свойством 3D-совместности, а следовательно, по определению (1.3) интегрируемо.

Из уравнения в квад-графах можно получить отображение Янга–Бакстера. В их графической интерпретации заметны сходства, за исключением того, что уравнение в квад-графах связывает вершины квадрата, а отображение Янга–Бакстера стороны.

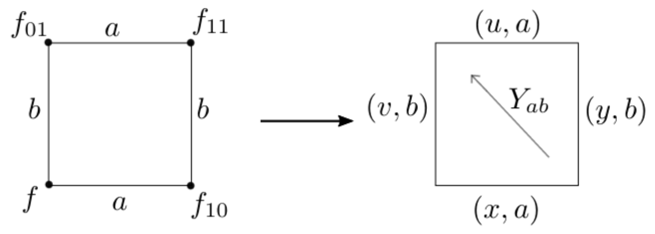
Рис. 4. Уравнение в квад-графах и отображение ЯБ

Покажем, что из уравнения КдФ (11) можно получить отображение Адлера. Перепишем каждую сторону как разность вершин:

Видно, что т. е. . Далее, т. е. .

Если решить систему из двух уравнений:

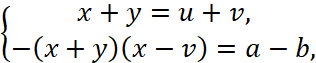, (14)

Относительно u и v, то получится отображение Адлера [1, с. 141-143]:

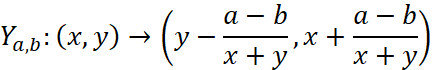, (15)

В работе выделены ключевые критерии интегрируемости уравнений на квад-графах. Уравнение является интегрируемым, если для него существует пара Лакса; более сильным условием служит 3D-совместность, которая позволяет алгоритмически строить решения. Эти подходы обеспечивают системное понимание и методы решения дискретных нелинейных систем, что иллюстрируется на примере дискретного потенциального уравнения Кортевега–де Фриза.