VTN-2. Истоки вращения: ранняя сверхгравитационная фаза, угловой момент и саморегулирующаяся архитектура Вселенной

Введение

Одним из наиболее недооценённых, но фундаментальных свойств наблюдаемой Вселенной является то, что большинство астрофизических объектов – от звёзд и планет до галактик и их чёрных дыр – обладают ненулевым угловым моментом. Вращение проявляется уже на самых ранних астрономических масштабах и играет ключевую роль в формировании структуры: определяет геометрию дисков, стабилизирует системы, регулирует аккрецию и определяет эволюцию компактных объектов.

Однако при стандартной гравитационной постоянной G₀ и классической линейной теории возмущений первичное формирование вращения оказывается динамически невозможно. В ранней Вселенной:

• гравитационная неустойчивость подавлена из-за малости G₀,
• плотностные флуктуации не достигают нелинейной стадии,
• сферическая симметрия компенсирует внутренние гравитационные поля,
• характерное время коллапса τ_coll многократно превосходит космическое время.

Без нелинейных центров сжатия не может возникнуть и угловой момент: вращение не может появиться прежде, чем будет создан гравитационный минимум, но такой минимум не может возникнуть при стандартной динамике. Это приводит к фундаментальному расхождению между моделью и наблюдениями.

Дополнительную трудность представляет существование сверхмассивных чёрных дыр с массами 10⁸–10¹⁰ M☉ на красных смещениях z≈6–10, чьи времена роста оказываются несовместимы со стандартным G₀. Даже максимально эффективная аккреция не позволяет достичь таких масс в доступные интервалы времени.

Эти несоответствия приводят к ключевому вопросу:
существовала ли в ранней Вселенной иная гравитационная динамика, отличная от современной?

В настоящей работе предлагается модель, основанная на гипотезе временной эволюции эффективной гравитационной постоянной, G_eff(t)=κ(t)·G₀. Усиление гравитации в раннюю эпоху (κ≫κ_crit) приводит к принципиально иной динамической картине:

1. Нелинейные центры сжатия (квазиявра) формируются неизбежно;
2. Эти квазиявра создают первичные гравитационные минимумы;
3. Появление минимальной асимметрии автоматически запускает рост углового момента;
4. Ранние сверхмассивные чёрные дыры возникают естественным образом;
5. Дальнейшая эволюция κ(t) стабилизируется за счёт голографического взаимодействия с Bulk;
6. Тёмная материя и тёмная энергия интерпретируются как следы ранних переходов кривизны между бранной и Bulk.

Bulk выполняет роль стабилизатора: он ограничивает рост κ(t), предотвращает глобальный коллапс и обеспечивает ступенчатое снижение гравитационной связности по мере формирования структуры. Это приводит к саморегулирующейся архитектуре ранней Вселенной и объясняет исчезновение условий, необходимых для образования новых сверхмассивных чёрных дыр в современную эпоху.

Предлагаемая модель даёт единое описание трёх ключевых феноменов:

• происхождения вращения,
• раннего формирования сверхмассивных объектов,
• природы тёмной материи и тёмной энергии.

Все они рассматриваются не как независимые загадки, а как взаимосвязанные следствия сверхгравитационной фазы и последующей стабилизации G_eff(t) в ходе взаимодействия браны с Bulk.

1. Вращение как фундаментальная космологическая аномалия

Одним из самых универсальных свойств астрофизических объектов является вращение. Ненулевой угловой момент обнаруживается на всех масштабах:

• у планетных систем,
• у звёзд и протозвёздных дисков,
• у галактик и их гало,
• у сверхмассивных чёрных дыр,
• у крупных космических структур.

Даже сверхмассивные чёрные дыры в центрах галактик обладают значительными вращениями, близкими к экстремальным. Угловой момент – не вторичный атрибут, а ключевой параметр, определяющий морфологию и эволюцию объектов.

Однако происхождение вращения остаётся одной из недооценённых фундаментальных проблем космологии. В стандартной модели с постоянной гравитационной постоянной G₀ нельзя естественно объяснить:

1. Когда и как во Вселенной появился ненулевой угловой момент;
2. Какие механизмы могли его породить на ранних стадиях;
3. Какие структуры должны были существовать, чтобы обеспечить передачу момента;
4. Как вращение связано с формированием первичных гравитационных ядер;
5. Почему вращающие объекты появляются так рано в истории Вселенной.

В стандартном сценарии (ΛCDM):

• до рекомбинации вещество жёстко связано с излучением;
• барионный компонент не может коллапсировать;
• флуктуации на большинстве масштабов не растут;
• гравитационных минимумов нет;
• без гравитационных минимумов не возникает асимметрии;
• без асимметрии угловой момент не может появиться.

Парадокс заключается в том, что вращение наблюдается уже на самых ранних масштабах, включая структуру протогалактических облаков и зарождение аккреционных дисков. Это требует наличия нелинейных центров сжатия, способных:

• концентрировать массу,
• поддерживать градиент потенциала,
• усиливать начальные асимметрии,
• обеспечивать механизм передачи момента.

Но такие центры не успевают возникнуть при G = G₀ в доступное космическое время.

Таким образом, наблюдаемое раннее вращение представляет собой прямое указание на то, что ранняя Вселенная обладала динамикой, отличной от той, что задаётся стандартной гравитационной постоянной G₀.

Эта проблема становится особенно острой при рассмотрении сверхмассивных чёрных дыр массами 10⁸–10¹⁰ M☉ на красных смещениях z ≈ 6–10. Их угловые моменты и темпы аккреции невозможно объяснить без существования ранних нелинейных гравитационных ядер, сформированных до периода галактической сборки.

В этом контексте вращение перестаёт быть частной характеристикой отдельных объектов и становится:

• космологическим индикатором ранней гравитационной динамики,
• маркером существования первичных гравитационных минимумов,
• следствием фазы, в которой гравитация была существенно выше G₀,
• доказательством невозможности объяснить структуру простым развитием небольших флуктуаций.

Всё это приводит к необходимости рассмотреть гипотезу о том, что ранняя Вселенная обладала усиленной, переменной гравитацией, которая обеспечила возникновение тех структур, что позже стали источниками и носителями углового момента.

2. Стандартная гравитационная динамика при G₀ и проблема отсутствия первичных структур

Классическая космология предполагает, что гравитационная постоянная G оставалась неизменной на протяжении всей истории Вселенной. Однако такая картина приводит к серьёзным противоречиям при попытке объяснить появление первых нелинейных структур и особенно – первичного вращения. При стандартном значении G₀ ранняя Вселенная оказывается динамически слишком «мягкой», чтобы сформировать гравитационные центры сжатия, необходимые для появления углового момента.

В этом разделе рассматриваются три ключевых механизма, которые совместно приводят к подавлению раннего коллапса при G₀.

2.1. Подавление линейного роста флуктуаций при G₀

В ранней Вселенной рост плотностных возмущений описывается уравнением линейной неустойчивости:

, (1)

До рекомбинации барионный компонент:

• динамически связан с излучением,
• испытывает значительное радиационное давление,
• обладает высокой скоростью распространения плазменных возмущений (скорость звука в фотон-барионной плазме),
• не может коллапсировать независимо от фотонов.

Для большинства масштабов в эту эпоху выполняется неравенство:

, (2)

Что означает:

гравитационное сжатие не успевает развиваться.

Возмущения:

• либо затухают,
• либо переходят в плазменные (акустические) колебания фотон-барионной среды,
• либо «размываются» расширением.

Флуктуации не достигают амплитуд, необходимых для перехода в нелинейный режим.

2.2. Компенсация гравитации внутри сферических слоёв

Даже если локальные неоднородности и возникают, они сталкиваются с фундаментальным ограничением: теоремой Ньютона о сферических оболочках.

Внутри любого сферического слоя результирующее гравитационное поле равно нулю.

Следствия:

1. Внутренние районы не испытывают дополнительного притяжения;
2. Внешние слои не вносят вклада во внутренний коллапс;
3. Градиент потенциала в глубине структуры крайне мал.

Это означает, что при малых значениях G₀ даже умеренные флуктуации не способны перейти в режим устойчивого сжатия – для этого требуется выраженная асимметрия, которой в ранней Вселенной ещё нет.

2.3. Несоответствие времён τ_coll и космического времени t

Характерное время гравитационного сжатия для однородной области можно оценить как:

, (3)

На ранних стадиях:

• значение G остаётся малым (G = G₀),
• плотность ρ ещё недостаточно велика,
• космическое время t крайне коротко.

В результате:

, (4)

И это справедливо для всех масштабов, кроме самых малых.

Отсюда следует:

• флуктуации практически не растут,
• гравитационная неустойчивость подавлена,
• нелинейные центры сжатия не успевают сформироваться,
• никакие устойчивые вращающиеся структуры не могут возникнуть.

Без гравитационного минимума нет механизма возникновения углового момента, поэтому появление вращения на ранних этапах эволюции становится невозможным.

2.4. Итог раздела 2

В модели с постоянной гравитационной постоянной G₀ ранняя Вселенная не способна произвести первые структуры. Причины:

1. Линейный рост флуктуаций подавлен из-за малости G₀ и доминирования расширения;
2. Сферическая компенсация уничтожает внутренние гравитационные градиенты;
3. Время гравитационного сжатия τ_coll многократно превосходит космическое время t;
4. Первые нелинейные ядра не успевают сформироваться;
5. Угловой момент не может возникнуть, так как нет гравитационных центров.

Следовательно, стандартная динамика при G₀ не объясняет появление первых вращающихся структур.

Это указывает на необходимость иной гравитационной фазы в ранней Вселенной, отличающейся от современной – то есть фазы усиленной, переменной гравитации. Эта гипотеза рассматривается в следующем разделе.

3. Гипотеза ранней сверхгравитационной фазы κ(t)

Результаты предыдущего раздела показывают, что при постоянной гравитационной постоянной G₀ в ранней Вселенной не формируются гравитационные минимумы, необходимые для возникновения углового момента и последующего роста структур. Наиболее естественным способом разрешить этот парадокс является предположение, что эффективная гравитационная постоянная в раннюю эпоху отличалась от современной.

Мы вводим параметр:

, (5)

Где G_eff(t) – эффективная гравитационная постоянная, принимающая большее значение в ранней Вселенной. Усиление гравитации означает κ > 1; современная эпоха соответствует κ ≈ 1.

3.1. Динамическая необходимость усиленной гравитации

Если κ(t) в ранней эпохе было существенно больше единицы, то:

1. Время гравитационного сжатия уменьшается: ,
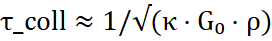2. Нелинейные центры сжатия начинают формироваться,
3. Гравитационная неустойчивость развивается быстрее,
4. Слабая асимметрия переходит в нелинейный режим,
5. Появляется геометрический градиент, необходимый для зарождения углового момента.

Существует критическое значение κ_crit, такое что:

• при κ < κ_crit – флуктуации остаются линейными,
• при κ > κ_crit – сжатие становится неизбежным и переходит в нелинейный режим.

Таким образом, ранняя сверхгравитационная фаза (κ ≫ κ_crit) является необходимым условием для формирования первичных структур.

3.2. Физическая интерпретация κ(t)

Параметр κ(t) не означает модификацию фундаментальных законов гравитации. Он описывает:

• эффективную величину гравитационного взаимодействия,
• возникающую из динамики голографического обмена кривизной между бранной и Bulk,
• влияние высокоразмерного домена на локальную метрику 4D.

Bulk выступает:

• регулятором гравитационной связности,
• аккумулятором избыточной кривизны,
• механизмом стабилизации после формирования структуры.

Таким образом, переменная гравитационная постоянная – не новая константа, а эффективный параметр, возникающий из геометрической архитектуры системы брана–Bulk.

3.3. Необходимость временной эволюции G_eff(t)

В отличие от моделей, предполагающих постоянное усиление гравитации, наша гипотеза требует временной эволюции κ(t):

• в раннюю эпоху – κ ≫ 1,
• после формирования первичных структур – постепенное снижение κ(t),
• в современную эпоху – κ → 1.

Причины:

1. При слишком большом κ ранняя Вселенная бы полностью коллапсировала.
2. При слишком малом κ структуры не появляются.
3. Для возникновения вращения необходимо пройти режим нелинейного сжатия.
4. Для прекращения роста сверхмассивных объектов необходимо снизить κ.
5. Для появления современного вида галактик требуется стабилизированная гравитация.

Такой сценарий приводит к ступенчатой эволюции κ(t), обсуждаемой в следующем разделе.

3.4. Итог раздела 3

Ранняя сверхгравитационная фаза – это не спекулятивное допущение, а динамическая необходимость, вытекающая из:

• невозможности роста флуктуаций при G₀;
• отсутствия ранних гравитационных минимумов;
• появления вращения уже на первых масштабах;
• существования ранних сверхмассивных чёрных дыр;
• наблюдаемой структуры Вселенной.

Гипотеза κ(t) естественным образом решает все эти проблемы, обеспечивая условия для возникновения квазиявров – первичных нелинейных центров сжатия, которые и становятся источниками углового момента.

В следующем разделе рассматривается математическое условие, при котором вращение становится неизбежным следствием усиленной гравитации.

4. Математическое условие неизбежности возникновения вращения при усиленной гравитации

В рамках гипотезы переменной гравитационной связности G_eff(t) = κ(t) · G₀ существенное усиление гравитации (κ ≫ 1) приводит к переходу плотностных флуктуаций в нелинейный режим. В этом режиме возникает ключевое свойство: любой малой асимметрии достаточно для того, чтобы запустить рост углового момента.

В этом разделе формулируется минимальный набор условий, при которых вращение появляется обязательно, а не как случайный эффект.

4.1. Нелинейный режим плотности при κ > κ_crit

Переход линейного возмущения δ(x,t) в нелинейную стадию достигается при:

, (6)

Основным временным масштабом является время коллапса:

, (7)

Для перехода к нелинейной стадии необходимо выполнение:

, (8)

Где t – космическое время на соответствующем этапе.

Отсюда следует критерий:

, (9)

Начнём прямо с ключевого вывода: κ > κ_crit ⇒ флуктуации неизбежно достигают нелинейной стадии.

4.2. Неустойчивость сферической симметрии

Сферическая симметрия в коллапсирующей среде нестабильна. Это следствие классической теоремы:

• любая сферическая конфигурация при нелинейном режиме становится неустойчивой к малым асферическим возмущениям.

Если δR/R – радиальная асимметрия, то возмущение моментально усиливается:

, (10)

При κ ≫ 1:

• рост асферичности становится экспоненциальным;
• симметрия разрушается;
• объект стремится к форме с минимальной энергией для данного момента инерции.

Это фундаментальный момент: усиленная гравитация сама создаёт условия для потери сферичности.

4.3. Появление углового момента из малой асимметрии

Угловой момент формируется в процессе нелинейного коллапса, когда:

1. Присутствует асферичность,
2. Существует градиент плотности,
3. Материя перераспределяется несимметрично.

Для коллапсирующей области:

, (11)

В отсутствие заведомой симметрии скорости и распределения массы (а в нелинейном режиме симметрия разрушена), интеграл становится ненулевым.

Минимальная «зерновая» асимметрия δ (даже квантового или теплового происхождения) даёт:

, (12)

Где I – момент инерции.

При κ ≫ 1:

L_nonlin значительно превосходит любой вклад линейных эффектов.

То есть: Если κ > κ_crit, вращение появляется неизбежно – его невозможно избежать даже при минимальных начальных отклонениях.

4.4. Рост углового момента в ходе коллапса

По мере уменьшения радиуса R:

• момент инерции I уменьшается,
• скорость вращения ω возрастает:

, (13)

Коллапс усиливает вращение по принципу:

(грубая оценка для сферических слоёв).

В режиме повышенной гравитации:

• коллапс идёт быстрее,
• R уменьшается стремительнее,
• следовательно, ω растёт значительно сильнее.

Это даёт естественное объяснение:

• раннего появления вращающихся структур,
• формирования аккреционных дисков,
• закрутки в протогалактиках,
• быстрых вращений сверхмассивных чёрных дыр.

4.5. Итог раздела 4

Усиленная гравитация (κ ≫ κ_crit) приводит к трём фундаментальным последствиям:

1. Флуктуации неизбежно переходят в нелинейный режим. τ_coll становится меньше космического времени t.
2. Сферическая симметрия становится динамически неустойчивой. Даже минимальное отклонение усиливается экспоненциально.
3. Возникает ненулевой угловой момент. Асферичность + несимметричное перераспределение массы = L ≠ 0.

Таким образом: появление вращения не требует специальных начальных условий.

Для его возникновения достаточно усиленной гравитации κ(t).

Это фундаментальный результат: вращение – не случайность и не внешнее воздействие, а неизбежное следствие усиленной гравитационной фазы.

5. Ступенчатая эволюция κ(t) и механизм саморегуляции гравитационной связности

Переход от ранней сверхгравитационной фазы к современному режиму G_eff ≈ G₀ не может происходить гладко. Формирование структуры – это нелинейный, неравновесный процесс, включающий коллапс, аккрецию, перераспределение массы и обмен кривизной между бранной и Bulk. В таких условиях изменения G_eff(t) должны иметь ступенчатый характер, отражающий последовательные этапы формирования и насыщения гравитационных структур.

5.1. Почему κ(t) не может уменьшаться монотонно

Если бы κ(t) уменьшалось плавно, без резких изменений, возникли бы два противоречия:

1. Слишком раннее снижение κ(t) привело бы к остановке коллапса, до того, как появились квазиявра и первые вращающие структуры;
2. Слишком позднее снижение κ(t) привело бы к чрезмерному росту компактности и глобальному коллапсу.

Таким образом, κ(t) должно:

• оставаться высоким до завершения формирования первичных ядер,
• снижаться после их появления,
• стабилизироваться после насыщения структуры.

Этот процесс нельзя описать непрерывной плавной функцией – он имеет внутренние пороги.

5.2. Пороговые значения κ и переходы между фазами

В структуре нелинейного коллапса неизбежно возникает несколько критических значений:

• κ_crit – порог нелинейности;
• κ_form – порог формирования устойчивых квазиявров;
• κ_sat – порог насыщения компактных объектов;
• κ_reg – порог стабилизации (современная эпоха).

Когда κ(t) пересекает эти пороги, динамика меняется скачкообразно, что естественным образом приводит к ступенчатой форме κ(t).

5.3. Физическая причина ступенчатой структуры: обратная связь с Bulk

Bulk играет роль голографического стабилизатора и «резервуара» кривизны. Когда структура переходит в новый динамический режим:

• изменяется характер коллапса;
• меняется распределение кривизны;
• часть кривизны передаётся в Bulk;
• меняется эффективная гравитационная постоянная κ(t).

Bulk реагирует не мгновенно, а с задержкой, зависящей от неравновесной динамики структуры. Это создаёт естественную основу для ступенчатых изменений κ(t).

Можно выделить три основные ступени:

1-я ступень: κ ≫ κ_crit – фаза формирования структуры:

• быстрый рост флуктуаций;
• формирование квазиявров;
• появление первых вращений.

Bulk фиксирует избыточную кривизну, но не ограничивает коллапс.

2-я ступень: κ_form → κ_sat – фаза насыщения структуры

По мере формирования компактных объектов:

• усиливается обмен кривизной с Bulk;
• повышается порог стабилизации;
• κ(t) начинает снижаться;
• рост компактности замедляется.

Происходит саморегуляция: система стремится к устойчивым конфигурациям.

3-я ступень: κ ≈ 1 – стабилизированная фаза

После насыщения структуры:

• гравитационные неустойчивости подавлены;
• Bulk стабилизирует кривизну на уровне современной динамики;
• G_eff(t) → G₀.

Новые сверхмассивные чёрные дыры больше не возникают, так как среда недостаточно связана гравитационно.

5.4. Геометрическая интерпретация ступенчатой функции κ(t)

Ступенчатый характер κ(t) отражает:

• наличие порогов в коллапсе,
• неравновесные переходы между фазами,
• дискретность гравитационных процессов в квазияврах,
• задержку отклика Bulk на изменения кривизны.

С математической точки зрения κ(t) представляет собой кусочно-непрерывную функцию, где каждая ступень соответствует определённому режиму эволюции:

κ(t) = κ₁ (фаза роста) κ(t) = κ₂ (фаза насыщения) κ(t) = κ₃ (фаза стабилизации) со сглаженными переходами между ними.

5.5. Итог раздела 5

Ступенчатая эволюция κ(t):

1. Разрешает противоречие между необходимостью сильной ранней гравитации и современной слабой;
2. Обеспечивает формирование квазиявров и первичного вращения;
3. Предотвращает глобальный коллапс;
4. Стабилизирует гравитацию после формирования структуры;
5. Объясняет прекращение формирования новых сверхмассивных чёрных дыр.

Таким образом, ступенчатый характер κ(t) – не допущение, а динамическое следствие нелинейной гравитационной эволюции и взаимодействия браны с Bulk.

6. Квазиявра как первичные гравитационные ядра ранней Вселенной

Переход флуктуаций в нелинейную стадию при усиленной гравитации (κ≫κ_crit) приводит к формированию объектов, которые не являются ни звёздами, ни обычными плотностными неоднородностями. Это квазиявра – первичные гравитационные ядра, являющиеся фундаментальными элементами ранней структуры Вселенной.

Квазиявра представляют собой локальные минимумы гравитационного потенциала (глубокие гравитационные ямы), возникающие в условиях:

• нестабильности сферической симметрии,
• усиленного коллапса при κ≫κ_crit,
• быстрых неравновесных процессов,
• асферичных перераспределений массы.

Они формируются раньше звёзд, раньше галактик и раньше сверхмассивных чёрных дыр – именно они создают условия для их появления.

6.1. Физическая природа квазиявров

Квазиявро – это нелинейная структура, возникающая из амплифицируемых асимметрий в плотности. В отличие от классического гравитационного коллапса при G₀, где требуется развитая структура или большое начальное возмущение, при κ≫κ_crit достаточно минимальной асферичности.

Основные свойства квазиявров:

• нелинейный режим (),
• глубокий минимум потенциала,
• устойчивый градиент плотности,
• внутреннее вращение, возникающее автоматически,
• способность концентрировать массу,
• длительное время жизни (не размываются расширением).

Квазиявро – это не объект в классическом смысле, а динамическая гравитационная форма, определяемая неравновесным характером раннего сжатия.

6.2. Почему квазиявра возникают неизбежно при κ≫κ_crit

Если κ превышает критическое значение κ_crit, выполняются три условия:

1. τ_coll < t – сжатие развивается быстрее расширения;
2. нестабильность сферической симметрии – минимальная асферичность растёт экспоненциально;
3. градиент плотности становится устойчивым, формируя локальный минимум.

Эти свойства обеспечивают автоматическое образование гравитационных ядер:

• не нужны большие начальные флуктуации,
• не требуется специальная геометрия,
• не нужны дополнительные поля или внешние воздействия.

Квазиявра – прямое динамическое следствие усиленной гравитации.

6.3. Квазиявра как источники углового момента

Вращение возникает в квазияврах неизбежно:

1. Нелинейный коллапс разрушает сферическую симметрию;
2. Перераспределение массы становится несимметричным;
3. Градиент плотности создаёт моменты сил;
4. Угловой момент L перестаёт быть равным нулю.

Для квазиявро справедлива оценка:

, (14)

Где δ – минимальная асимметрия. При κ≫κ_crit даже δ ~ 10⁻⁶ приводит к значимому L.

Таким образом: квазиявры – первые вращающиеся объекты Вселенной.

Они задают угловой момент:

• протогалактикам,
• будущим аккреционным дискам,
• ядрам галактик,
• предшественникам сверхмассивных чёрных дыр.

6.4. Квазиявра как семена ранних сверхмассивных чёрных дыр

При достаточно высокой плотности и продолжительном коллапсе квазиявра:

• концентрируют массу,
• увеличивают глубину потенциала,
• ускоряют аккрецию,
• создают условия для перехода в ультракомпактный объект.

Это делает квазиявра естественными предшественниками ранних сверхмассивных чёрных дыр (SMBH). Они обеспечивают:

• достаточный гравитационный градиент,
• внутреннее вращение,
• быстрый рост компактности,
• отсутствие необходимости в больших первичных флуктуациях.

Все наблюдаемые ранние SMBH (z ≈ 6–10) требуют существования таких ядер.

6.5. Почему квазиявра не существуют в современную эпоху

Квазиявра могут формироваться только в условиях:

• усиленной гравитации (κ≫κ_crit),
• отсутствия развитой крупномасштабной структуры,
• высокой нелинейности,
• интенсивного обмена кривизной с Bulk.

Когда κ(t) снижается к ≈1, а структура уже сформирована:

• коллапс замедляется,
• нелинейные центры возникают только в чрезвычайно компактных условиях,
• симметрия меньше нарушается,
• градиенты плотности слабее.

Поэтому в современную эпоху квазиявра больше не возникают – они являются реликтом ранней сверхгравитационной фазы.

6.6. Итог раздела 6

Квазиявра – фундаментальный элемент космологической эволюции:

1. Возникают неизбежно при усиленной гравитации;
2. Формируют первые нелинейные гравитационные центры;
3. Порождают первичное вращение;
4. Обеспечивают необходимые условия для ранних сверхмассивных чёрных дыр;
5. Исчезают после снижения κ(t), будучи реликтом ранней Вселенной.

Таким образом, квазиявра – это связующее звено между усиленной гравитацией κ≫κ_crit, появлением углового момента и формированием сверхмассивных чёрных дыр.

Следующий раздел рассматривает механизм, который ограничивает усиленную гравитацию и предотвращает глобальный коллапс – роль Bulk как стабилизатора.

7. Роль Bulk как стабилизатора G_eff(t) и ограничителя раннего коллапса

Усиленная гравитационная связность в раннюю эпоху (κ≫κ_crit) приводит к неизбежному формированию нелинейных гравитационных ядер и вращающихся структур. Однако если бы κ(t) оставалось большим и после формирования структуры, ранняя Вселенная столкнулась бы с двумя фундаментальными угрозами:

1. Глобальным ускорением коллапса,
2. Неограниченным ростом компактных объектов вплоть до разрушения крупномасштабной структуры.

Это означает, что усиленная гравитация должна быть не только введена, но и стабилизирована. Стабилизацию обеспечивает не сама брана, а связанный с ней высокоразмерный голографический домен Bulk, который играет роль регулятора G_eff(t).

Bulk не вводится как новая физическая сущность; он представляет собой геометрический слой, взаимодействующий с бранной через обмен кривизной. Это взаимодействие определяет динамику эффективной гравитации.

7.1. Зачем необходим механизм стабилизации

Если κ(t) остаётся слишком большим после формирования квазиявров и ранних компактных структур:

• коллапс продолжается без насыщения;
• объекты становятся всё более компактными;
• локальная кривизна растёт быстрее, чем успевает перераспределяться;
• возникают конфигурации, несовместимые с наблюдаемой крупномасштабной структурой.

Система требует механизма, который:

1. Поглощает избыточную кривизну,
2. Ограничивает дальнейший рост κ(t),
3. Обеспечивает переход к режиму κ → 1.

Bulk выполняет именно эту функцию.

7.2. Голографический обмен кривизной между бранной и Bulk

При формировании нелинейных структур возникает избыток локальной кривизны, который невозможно сохранить в чисто четырёхмерной динамике без разрушения структуры.

В модели брана–Bulk:

• брана – это 4-мерная метрика, где происходит формирование структуры;
• Bulk – высокоразмерный геометрический домен, способный принимать часть кривизны.

Обмен кривизной происходит в форме:

• перераспределения геометрической энергии,
• изменения эффективной глубины гравитационных потенциалов,
• корректировки локальной связности.

Когда формируется квазиявро или начинается рост сверхкомпактного объекта, избыточная кривизна передаётся в Bulk, уменьшая эффективную гравитационную силу на бране.

Это приводит к снижению κ(t).

7.3. Bulk как механизм предотвращения глобального коллапса

Если бы обмен кривизной отсутствовал, усиленная гравитация привела бы к:

• быстрому коллапсу крупных областей,
• исчезновению масштабной структуры,
• невозможности существования современной Вселенной.

Bulk выполняет роль автоматического стабилизатора:

• он реагирует на рост компактности;
• выводит избыточную кривизну за пределы браны;
• снижает эффективную связность вслед за формированием структур;
• сглаживает неравновесные переходы.

Это создаёт саморегулирующуюся архитектуру, где рост структуры вызывает снижение G_eff(t).

7.4. Почему стабилизация должна быть ступенчатой

Гравитационный обмен между бранной и Bulk не мгновенный и не непрерывный:

• он инициируется, когда структура достигает определённой компактности;
• действует только при переходах между динамическими фазами;
• происходит на фоне нелинейных процессов коллапса.

Поэтому снижение κ(t):

• происходит порциями,
• соответствует переходам между фазами,
• образует ступенчатую функцию, обсуждённую в Разделе 5.

Каждая ступень отражает очередной этап достижения структурной насыщенности.

7.5. Итог раздела 7

Bulk обеспечивает:

1. Поглощение избыточной кривизны, возникающей при κ≫κ_crit;
2. Ограничение роста компактности в нелинейных структурах;
3. Предотвращение глобального коллапса;
4. Ступенчатое снижение κ(t) вслед за формированием структуры;
5. Переход к современному режиму G_eff ≈ G₀.

Таким образом, Bulk играет ключевую роль в динамике ранней Вселенной: он завершает эпоху сверхгравитации и обеспечивает переход к стабильному эволюционному режиму.

Следующий раздел покажет, как эта комбинация (κ≫κ_crit и стабилизация Bulk) приводит к естественному и неизбежному появлению ранних сверхмассивных чёрных дыр.

8. Ранняя сверхгравитационная фаза и формирование сверхмассивных чёрных дыр

Наблюдения показывают существование сверхмассивных чёрных дыр (SMBH) массой уже на красных смещениях z ≈ 6–10. Это означает, что такие объекты сформировались в течение первых 500–800 млн лет после Большого взрыва.

При стандартной гравитации G₀ и разумных сценариях аккреции такие массы недостижимы: ни рост сидов, ни аккреция Эддингтона не позволяют накопить столь большую массу за столь короткое время.

В рамках модели переменной гравитации ранние SMBH возникают не как исключение, а как естественное следствие сверхгравитационной фазы κ≫κ_crit и формирования квазиявров.

8.1. Квазиявра как естественные сида для SMBH

Квазиявра – это первичные нелинейные гравитационные минимумы, формирующиеся при усиленной гравитации. Их ключевые свойства:

• локальное усиление плотности,
• устойчивый гравитационный градиент,
• высокая асферичность,
• внутреннее вращение,
• способность концентрировать массу.

Эти свойства делают квазиявра: идеальными сидами для ранних сверхмассивных чёрных дыр.

В отличие от стандартных сценариев, которым требуется:

• большой начальный сид (),
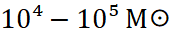• тонко настроенная аккреция,
• резкие поглощения газа.

В нашей модели зародышевые гравитационные ядра формируются автоматически – как непосредственное следствие κ≫κ_crit.

8.2. Усиленная аккреция при κ≫κ_crit

При увеличении гравитационной связности G_eff:

• ускоряется падение вещества;
• растёт скорость захвата газа;
• увеличивается глубина потенциальной ямы;
• усиливается вращение, способствуя аккреции в диски;
• появляется возможность квази-Эддингтоновской или даже сверх-Эддингтоновской аккреции.

Иными словами, усиленная гравитация ускоряет все механизмы роста, делая раннее появление SMBH естественным.

Аккреционные времена в условиях κ≫κ_crit уменьшаются в √κ раз:

, (15)

Даже умеренное усиление κ даёт многократное сокращение времени роста.

8.3. Ускоренное сжатие в квазияврах

Внутри квазиявра формируется глубокий гравитационный минимум. При κ≫κ_crit:

• плотность растёт быстрее,
• сжатие идёт по нелинейному сценарию,
• объёмная скорость аккреции увеличивается,
• система становится всё более компактной.

В результате образование ультракомпактных объектов становится не только возможным, но и неизбежным.

Это объясняет тот факт, что: SMBH появляются раньше, чем должны при стандартной динамике G₀.

8.4. Согласование с наблюдениями

Наблюдаемая популяция ранних SMBH обладает следующими свойствами:

• высокие массы, недостижимые при G₀;
• высокие вращения;
• большие темпы аккреции;
• быстрый рост в первые сотни миллионов лет.

Все эти свойства естественны в рамках усиленной гравитации κ≫κ_crit:

1. Квазиявра задают стартовую компактность и вращение;
2. Усиленная аккреция обеспечивает быстрый рост;
3. Плотные протогалактические среды ускоряют слияния малых сидов;
4. Стабилизация Bulk ограничивает дальнейший рост (см. раздел 9).

Таким образом, модель дает невероятно простое объяснение ранних SMBH: они – побочный продукт сверхгравитационной фазы, а не аномалия.

8.5. Критическая роль стабилизации Bulk

Bulk ограничивает рост SMBH:

• по мере увеличения компактности усиливается обмен кривизной с Bulk,
• часть гравитационной глубины переносится в голографический слой,
• κ(t) начинает снижаться,
• рост SMBH переходит в режим насыщения.

Именно этот механизм:

• предотвращает образование сверхмассивных монстров (),
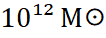• ограничивает массу чёрных дыр в ранней Вселенной,
• обеспечивает согласованность с наблюдаемым распределением масс.

8.6. Итог раздела 8

Ранняя сверхгравитационная фаза обеспечивает:

1. Формирование квазиявров – первых гравитационных ядер;
2. Быстрый рост компактности и вращения;
3. Ускоренную аккрецию вещества;
4. Появление сверхмассивных чёрных дыр в раннюю эпоху;
5. Ограничение роста SMBH за счёт стабилизации Bulk.

Таким образом, ранние сверхмассивные чёрные дыры – не загадка, а естественное, неизбежное и закономерное следствие κ≫κ_crit.

В следующем разделе рассматривается причина, по которой в современную эпоху такие объекты больше не формируются.

9. Почему в современную эпоху новые сверхмассивные чёрные дыры не образуются при G≈G₀

Формирование сверхмассивных чёрных дыр (SMBH) в ранней Вселенной было следствием усиленной гравитационной фазы κ≫κ_crit, обеспечившей быстрый рост компактности, ускоренную аккрецию и появление нелинейных гравитационных ядер – квазиявров. Однако по мере эволюции структуры обмен кривизной между бранной и Bulk приводил к постепенному снижению κ(t), и в современную эпоху эффективная гравитационная постоянная стабилизировалась на уровне G_eff ≈ G₀.

Это означает, что условия, необходимые для возникновения новых SMBH, больше не существуют. Ниже разбираются основные причины.

9.1. Ослабление гравитационной связности: κ → 1

В современной Вселенной:

• гравитационный градиент слабее, чем в раннюю эпоху;
• время сжатия τ_coll становится вновь слишком большим;
• коллапс не может перейти в режим, необходимый для образования ультракомпактных объектов.

При G≈G₀ выполняется:

, (16)

Где t_dyn – характерное время динамических процессов в галактических ядрах.

Это означает: новые нелинейные центры сжатия больше не рождаются.

9.2. Исчезновение условий для формирования квазиявров

Квазиявра формировались при κ≫κ_crit. При κ≈1:

• сферическая симметрия сохраняется дольше,
• асимметрии хуже усиливаются,
• нелинейные градиенты плотности почти не растут,
• гравитационные минимумы формируются только в экстремальных случаях (например, коллапс массивной звезды).

В обычных условиях: квазиявра больше не возникают.

А без квазиявров нет первичных сидов для SMBH.

9.3. Разреженность среды и недостаток плотности

Условия ранней Вселенной (z > 10):

• высокая средняя плотность,
• обилие холодного газа,
• быстрые темпы аккреции.

Современная эпоха:

• плотность межгалактической среды на порядки ниже,
• газ в галактиках более нагрет,
• давление выше,
• аккреция менее эффективна.

Это подавляет любые сценарии быстрого роста:

, (17)

С уменьшением G_eff и ρ темп роста объектов падает катастрофически.

9.4. Порог стабилизации: ограничение роста со стороны Bulk

Bulk стабилизирует G_eff(t) и препятствует чрезмерной компактности в поздние эпохи:

• избыточная кривизна немедленно перераспределяется;
• гравитационные потенциалы «сглаживаются»;
• образование ультракомпактных структур подавляется.

Если в ранней эпохе Bulk ограничивал чрезмерный рост SMBH, то в поздней – он фактически запрещает формирование новых.

9.5. Аккреция и слияния недостаточны без первичного ядра

Сегодня:

• аккреция идёт медленно,
• слияния не дают большой массы без первоначального компактного сида,
• не существует механизма, способного резко увеличить плотность.

Даже длительные (многомиллиардолетние) процессы не могут воспроизвести условия ранней сверхгравитации.

9.6. Современные чёрные дыры – эволюционные остатки, а не новые объекты

Все наблюдаемые SMBH:

• либо реликты раннего роста,
• либо увеличившиеся за счёт длительных аккреций и слияний.

Современная структура Вселенной не содержит регионов, где:

• плотность достаточна,
• компактность высока,
• κ(t) велико,
• симметрии разрушены быстро,
• коллапс проходит нелинейную стадию.

9.7. Итог раздела 9

В современной Вселенной новые сверхмассивные чёрные дыры не могут образоваться. Причины:

1. κ(t) снизилось до ≈1, и гравитационная связность ослабла.
2. Квазиявра больше не возникают – нет первичных нелинейных ядер.
3. Плотность среды недостаточна для быстрого роста.
4. Bulk стабилизирует кривизну и подавляет ультракомпактные конфигурации.
5. Аккреция и слияния без квазиявра не дают сверхмассивных объектов.
6. Современные SMBH – реликты ранней сверхгравитационной эпохи.

Таким образом: ранние SMBH – естественное следствие κ≫κ_crit, а современные условия – естественный запрет на их новое образование.

Следующий раздел (10) рассматривает происхождение тёмной материи как локального гравитационного следа ранних переходов кривизны.

10. Тёмная материя как голографический след ранних переходов кривизны

В предыдущих разделах показано, что ранняя Вселенная пережила фазу усиленной гравитации (κ≫κ_crit), при которой происходили нелинейные переходы плотности, формирование квазиявров и быстрый рост гравитационных ядер. Эти процессы сопровождались неравновесным обменом кривизной между бранной и Bulk.

В результате часть локальной кривизны, возникшей в фазе κ≫κ_crit, не была полностью передана в Bulk, но сохранилась на бране в виде устойчивого, локализованного гравитационного следа.

Этот след и есть то, что в современной космологии наблюдается как тёмная материя.

10.1. Почему частицы не требуются

В модели VTN-2 тёмная материя:

• не является частицами,
• не является новым видом вещества,
• не требует WIMP-кандидатов,
• не требует изменений тензора энергии-импульса T_μν,
• не нарушает общую теорию относительности.

DM – это локализованная кривизна, оставшаяся после ранних переходов G_eff(t), а не «материя» в привычном для физики смысле.

С точки зрения наблюдателя, она ведёт себя как:

• дополнительная масса,
• дополнительная глубина потенциала,
• ненулевая компонента гало.

Но её природа – геометрическая, а не субстанциальная.

10.2. Механизм образования тёмной материи

Рассмотрим последовательность событий в сверхгравитационной фазе κ≫κ_crit:

1. Возникают квазиявра – первичные нелинейные гравитационные ямы.
2. Их рост создаёт избыток локальной кривизны.
3. Bulk перераспределяет часть этой кривизны, снижая κ(t).
4. Часть кривизны остаётся на бране, не переходя в Bulk полностью.
5. Эта оставшаяся часть фиксируется гравитационной структурой.

Она сохраняет форму, определённую:

• глубиной квазиявра,
• его асферичностью,
• скоростью роста компактности,
• распределением плотности в тот момент.

Именно этот «замороженный» след кривизны и соответствует современной тёмной материи.

10.3. Локализованная природа тёмной материи

Тёмная материя распределена:

• локально,
• вокруг галактик,
• вокруг их гало,
• вокруг кластеров,
• в местах первичных квазиявров.

Это объясняется тем, что именно там:

• были самые сильные нелинейные переходы,
• возникали наиболее глубокие гравитационные минимумы,
• шёл максимальный обмен кривизной с Bulk.

Таким образом: тёмная материя – это локальный остаток ранних структурообразующих процессов.

Она не распределена равномерно, потому что:

• переходы κ(t) происходили локально,
• компактность и нелинейность были неоднородны,
• квазиявра возникали только в отдельных местах.

10.4. Почему тёмная материя невидима

Поскольку DM – это не вещество, а кривизна:

• у неё нет взаимодействий с фотонами,
• нет сечений столкновений,
• нет барионного давления,
• нет собственных возбуждений.

Она проявляется только через:

• искривление геодезических,
• вращение галактик,
• линзирование,
• динамику кластеров.

То есть через эффективную массу, но не через частицы.

10.5. Соответствие распределению тёмной материи в ΛCDM

Несмотря на иную природу, DM в модели VTN-2:

• точно воспроизводит гало галактик,
• даёт корректные кривые вращения,
• объясняет стабильность дисков,
• обеспечивает динамику кластеров,
• согласуется с крупномасштабной структурой.

Причина проста:

• квазиявра → ядра галактик,
• ядра → распределение кривизны,
• распределение кривизны → профиль вращения.

Формально результат совпадает с предсказаниями ΛCDM, но: физическая причина другая: DM – не частицы, а геометрия.

10.6. Почему тёмная материя стабилизирует галактики

Тёмная материя как локализованная кривизна:

• не рассеивается,
• не нагревается,
• не взаимодействует диссипативно,
• сохраняет гало даже при взаимодействиях галактик.

Это объясняет:

• устойчивость вращения,
• долгоживущие гриппы гало,
• устойчивость дисков.

DM – это не дополнительная масса, а статическая геометрическая компонента, встроенная в структуру пространства.

10.7. Итог раздела 10

В рамках модели VTN-2 тёмная материя:

1. Возникает в ранней сверхгравитационной фазе как локальный остаток кривизны,
2. Связана с неравновесными переходами между бранной и Bulk,
3. Фиксируется структурами, возникшими в эпоху κ≫κ_crit,
4. Не является веществом и не требует новых частиц,
5. Полностью гравитационна и взаимодействует только через потенциал,
6. Соответствует наблюдаемой картине ΛCDM,
7. Является прямым «геометрическим следом» формирования квазиявров и ранних SMBH.

Следующий раздел касается тёмной энергии – второй компоненты, возникающей не локально, а как глобальный остаток переходов между бранной и Bulk.

11. Тёмная энергия как нелокальный остаток снижения κ(t)

В предыдущем разделе было показано, что тёмная материя (DM) является локализованным остатком ранних переходов кривизны в условиях усиленной гравитации κ≫κ_crit. Однако снижение κ(t) после формирования структуры имело не только локальные, но и глобальные последствия: не вся избыточная кривизна была перераспределена локально или поглощена Bulk. Часть её сформировала нелокальный геометрический фон, сохраняющийся в современной Вселенной.

Именно этот фон интерпретируется как тёмная энергия (DE).

11.1. Проблема космологической постоянной и её альтернативная интерпретация

В стандартной ΛCDM-модели тёмная энергия вводится как:

• либо космологическая постоянная Λ,
• либо вакуумная энергия,
• либо дополнительное поле.

Однако величина Λ противоречит квантовым оценкам на десятки порядков и не связана с историей формирования структуры.

В модели VTN-2 тёмная энергия интерпретируется по-другому.

DE – это: нелокальный гравитационный остаток глобального снижения κ(t), сформированный в ходе перехода от сверхгравитационной фазы к G_eff ≈ G₀.

Это не новый вид энергии, а геометрический след, встроенный в метрику браны.

11.2. Глобальное снижение κ(t) и перераспределение кривизны

Переход от κ≫κ_crit к κ≈1 происходил в несколько этапов (см. раздел 5):

1. Формирование нелинейных структур;
2. Насыщение квазиявров;
3. Ограничение роста компактности;
4. Стабилизация Bulk;
5. Снижение G_eff(t) до современного уровня.

На каждом этапе:

• Часть кривизны локализовалась → дала DM;
• Часть кривизны уходила в Bulk;
• Часть оставалась на бране в виде нелокального распределённого потенциала.

Именно эта нелокальная компонента определяет эффект ускоренного расширения.

11.3. Тёмная энергия как гравитационный фон, а не вещество

DE в модели VTN-2:

• не обладает локальной плотностью,
• не связана с частицами,
• не взаимодействует с материей,
• не имеет собственных возбуждений.

Она проявляется как:

• мягкий, распределённый гравитационный фон,
• формирующий эффективное «отталкивающее» действие на больших масштабах,
• аналог космологической постоянной, но с другим физическим происхождением.

DE – это остаточная, нелокализованная кривизна, возникшая из глобального перераспределения G_eff(t).

11.4. Отличие тёмной энергии от тёмной материи

Различия между DM и DE фундаментальны:

Тёмная материя (DM):

• локальна,
• привязана к структурам,
• повторяет контуры гало,
• фиксируется в областях бывших квазиявров.

Тёмная энергия (DE):

• нелокальна,
• распределена по всей бране,
• не образует гало,
• не зависит от структуры конкретных объектов.

Причина различий:

• DM = локальные переходы κ(t),
• DE = глобальные переходы κ(t).

Они возникают из одного механизма, но в разных его частях.

11.5. Геометрическая интерпретация деформаций метрики

С математической точки зрения:

• DM – это искривление потенциала Φ(x) вокруг структур,
• DE – это аддитивная, однородная компонента в метрике,
• κ(t) влияет на знак и величину производных метрики,
• Bulk задаёт граничные условия.

Устойчивая нелокальная компонента действует как:

• мягкий отрицательный эффективный вклад в ускорение,
• аналог Λ,
• след ранней саморегуляции G_eff(t).

11.6. Связь с ускоренным расширением Вселенной

Когда κ(t) снизилось до значения, близкого к 1, оставшийся нелокализованный гравитационный фон:

• не исчез,
• не был ассимилирован Bulk,
• сохранил свою форму в метрике.

Этот фон создаёт:

• медленно изменяющееся «растягивающее» действие,
• космологическое ускорение,
• вклад, идентичный Λ по наблюдаемым эффектам.

Таким образом: ускоренное расширение – это след ранней гравитационной эволюции, а не отдельная энергоформа.

11.7. Итог раздела 11

Тёмная энергия является:

1. Нелокальным остатком глобального снижения κ(t);
2. Гравитационным фоном, распределённым по всей бране;
3. Следствием перераспределения кривизны между бранной и Bulk;
4. Аналогом Λ, но с естественным происхождением;
5. Компонентой, не требующей новых полей или частиц;
6. Частью единого механизма, порождающего DM, DE и раннее вращение.

Таким образом, тёмная энергия не вводится искусственно – она является неизбежным результатом саморегулирующейся гравитационной архитектуры ранней Вселенной.

В следующем разделе рассматривается общий энергетический баланс между бранной и Bulk, объединяющий происхождение DM и DE в единую геометрическую схему.

12. Энергетический баланс брана–Bulk: локальные и нелокальные остатки кривизны

Механизм ранней сверхгравитационной фазы κ≫κ_crit сопровождался интенсивными переходами кривизны между бранной и Bulk. Эти переходы происходили в условиях:

• нелинейного роста плотности,
• формирования квазиявров,
• ускоренного коллапса,
• асферичного перераспределения массы,
• ступенчатого снижения κ(t).

Так как гравитационная энергия в общей теории относительности не локализуема, а сама гравитация описывается через геометрию, то переходы кривизны между бранной и Bulk не нарушают законов сохранения, а требуют трактовки, основанной на:

• геометрической интерпретации энергии,
• нелокальности гравитационного взаимодействия,
• роли голографических граничных условий.

В этом разделе формулируется финальная, целостная схема энергетического баланса между бранной и Bulk.

12.1. Почему в GR нельзя локализовать гравитационную энергию

В общей теории относительности:

• гравитационное поле не имеет собственной плотности энергии;
• энергия гравитации входит в геометрию, а не в тензор T_μν;
• любые плотности энергии гравитации являются координатно-зависимыми псевдотензорами.

Это означает: обмен кривизной между разными геометрическими областями не является нарушением энергосохранения – это изменение распределения геометрии.

Поэтому передача избыточной кривизны из браны в Bulk и сохранение части кривизны в локальных и нелокальных формах (DM и DE) полностью согласуются с GR.

12.2. Локальный остаток кривизны → тёмная материя

Часть избыточной кривизны, возникшей в фазе κ≫κ_crit:

• возникала локально – вокруг квазиявров;
• была связана с нелинейными структурами;
• не передалась полностью в Bulk;
• закрепилась на бране как локализованный гравитационный минимум.

Эта часть определяет:

• профили гало,
• стабильность вращения,
• динамику кластеров.

Это и есть: тёмная материя – локализованный геометрический след структурообразования.

12.3. Нелокальный остаток кривизны → тёмная энергия

Когда κ(t) снижалось к ≈1:

• происходили глобальные перераспределения кривизны,
• Bulk принимал большую часть избыточной компактности,
• но часть кривизны оставалась не в виде локальных ядер, а распределённым фоном.

Этот фон:

• не локализован,
• не привязан к структуре,
• проявляется как мягкое ускоряющее действие,
• соответствует космологической постоянной по наблюдаемым эффектам.

Это: тёмная энергия – нелокальный остаток глобального снижения κ(t).

12.4. Роль Bulk: аккумулятор и регулятор кривизны

Bulk обеспечивает:

1. Поглощение избыточной кривизны,
2. Стабилизацию κ(t) после формирования структур,
3. Предотвращение глобального коллапса,
4. Граничные условия для браны,
5. Отвод «излишнего» гравитационного потенциала,
6. Формирование нелокального остаточного фона (DE).

Bulk не создаёт новые формы энергии. Он:

• перераспределяет геометрию,
• регулирует баланс между локальными и глобальными компонентами,
• определяет конечное состояние G_eff(t) → G₀.

12.5. Совокупный баланс брана–Bulk

Эволюция ранней Вселенной в модели VTN-2 может быть выражена в виде единой схемы баланса:

1. κ≫κ_crit → усиленное сжатие → рост избытка кривизны.
2. Часть избытка фиксируется локально (DM).
3. Часть передаётся в Bulk (стабилизация).
4. Часть остаётся на бране как нелокальный фон (DE).
5. После формирования структуры κ(t) снижается к ≈1.
6. Система брана+Bulk становится самосогласованной и стабильной.

Таким образом: DM + DE + стабилизация Bulk – это разные проявления одного геометрического механизма перераспределения кривизны.

12.6. Итог раздела 12

1. Гравитационная энергия в GR – геометрическая, а не локальная, поэтому обмен кривизной между бранной и Bulk не нарушает закона сохранения.
2. Тёмная материя – локализованный остаток ранних нелинейных переходов κ(t), закрепленный в квазияврах.
3. Тёмная энергия – нелокализованная компонента, возникшая при глобальном снижении κ(t).
4. Bulk действует как регулятор кривизны и ограничитель ранней сверхгравитационной динамики.
5. Единственный механизм обеспечивает происхождение DM, DE и стабилизацию G_eff(t).
6. Система брана–Bulk является энергетически замкнутой, но распределение кривизны между её частями изменялось в ходе эволюции.

Следующий раздел – Заключение, где мы соберём общую картину и выделим ключевые результаты.

13. Заключение

В статье предложена модель ранней космологической эволюции, основанная на гипотезе временной усиленной гравитационной связности κ(t)=G_eff/G₀≫1. Показано, что эта фаза необходима для объяснения возникновения первичных гравитационных структур, появления углового момента и формирования сверхмассивных чёрных дыр в раннюю эпоху. Модель объединяет происхождение вращения, тёмной материи и тёмной энергии в единую геометрическую схему, в которой ключевую роль играет взаимодействие брана–Bulk.

Основные результаты работы можно сформулировать следующим образом.

13.1. Усиленная гравитация как условие формирования структуры

При стандартном значении G₀ ранняя Вселенная не может породить первичные нелинейные структуры:

• линейный рост флуктуаций подавлен,
• сферическая симметрия стабилизирует внутренние слои,
• время коллапса τ_coll многократно превосходит космическое время t.

Усиление гравитационной связности до κ≫κ_crit приводит к переходу флуктуаций в нелинейный режим и формированию первичных гравитационных минимумов.

13.2. Квазиявра как нелинейные ядра и источники углового момента

В условиях κ≫κ_crit неизбежно формируются квазиявра – нелинейные гравитационные ядра, возникающие при разрушении сферической симметрии. Они представляют собой:

• первые устойчивые центры компактности,
• источники внутреннего вращения,
• зачатки будущих галактических структур,
• естественные сиды ранних сверхмассивных чёрных дыр.

Минимальная асферичность в условиях усиленной гравитации приводит к появлению ненулевого углового момента, что объясняет происхождение вращения на самых ранних этапах.

13.3. Формирование ранних сверхмассивных чёрных дыр

При κ≫κ_crit:

• ускоряется аккреция,
• углубляются гравитационные минимумы,
• усиливается вращение,
• сокращается время роста компактности.

Это делает раннее появление сверхмассивных чёрных дыр массами естественным следствием эволюции, а не аномалией. Их современное распределение соответствует сидовой популяции, возникшей в сверхгравитационной эпохе.

13.4. Роль Bulk как стабилизатора κ(t)

Bulk обеспечивает:

• поглощение избыточной кривизны,
• ограничение роста сверхкомпактных структур,
• предотвращение глобального коллапса,
• ступенчатое снижение κ(t) по мере насыщения структуры,
• переход к современному режиму G_eff ≈ G₀.

Таким образом, Bulk формирует механизм саморегуляции ранней динамики.

13.5. Происхождение тёмной материи и тёмной энергии

Тёмная материя и тёмная энергия не вводятся как новые формы вещества; они являются геометрическими следами перераспределения кривизны в эпоху перехода κ≫κ_crit → κ≈1.

• Тёмная материя (DM) – локализованный остаток ранних нелинейных переходов, закреплённый в областях бывших квазиявров.
• Тёмная энергия (DE) – нелокализованный фон, возникающий из глобального снижения κ(t) и проявляющийся как ускоренное расширение.

Обе компоненты являются различными проявлениями единого механизма.

13.6. Современная Вселенная как стабилизированная геометрическая система

После стабилизации κ(t) до значения, близкого к 1:

• новые квазиявра не возникают,
• формирование новых SMBH становится невозможным,
• структура Вселенной принимает современный вид,
• локальные и глобальные остатки кривизны (DM и DE) формируют наблюдаемую динамику.

Таким образом, современная космологическая картина является завершённым этапом эволюции системы брана–Bulk.

13.7. Итог

Модель VTN-2 показывает, что:

1. Ранняя усиленная гравитация необходима для объяснения появления вращения и структур;
2. Квазиявра – фундаментальные элементы ранней Вселенной;
3. Ранние SMBH – естественное следствие κ≫κ_crit;
4. Bulk – стабилизатор гравитационной архитектуры;
5. DM и DE – геометрические остатки ранней эволюции κ(t);
6. Современная Вселенная – самосогласованная система с κ≈1.

Предложенная схема представляет собой саморегулирующуюся архитектуру, где формирование структуры, появление вращения и разграничение тёмных компонент – следствия единого процесса перераспределения кривизны между бранной и Bulk.

Эпилог

Представленная модель ранней Вселенной объединяет несколько, казалось бы, независимых космологических феноменов – возникновение вращения, раннее формирование сверхмассивных чёрных дыр, структуру тёмной материи и природу тёмной энергии – в единую геометрическую схему.

В её основе лежит простая идея: гравитационная связность не была одинаковой на всех этапах истории Вселенной. Ранняя сверхгравитационная фаза, неизбежно порождающая нелинейные гравитационные ядра и первичное вращение, сменялась стабилизирующим снижением κ(t) под действием голографических граничных условий Bulk. Это привело к формированию саморегулирующейся архитектуры, в которой локальные и нелокальные остатки переходов кривизны сохранились как тёмная материя и тёмная энергия.

В этой картине наблюдаемая Вселенная – результат динамического согласования между:

• исходно высоким значением эффективной гравитационной связности на ранних этапах эволюции,
• формированием нелинейных структур,
• перераспределением кривизны между бранной и Bulk,
• стабилизацией G_eff(t) до современного уровня.

Такое описание позволяет рассматривать крупномасштабную структуру, галактическую динамику и ускоренное расширение не как набор разрозненных феноменов, а как следствия единого процесса – постепенного выравнивания гравитационной архитектуры по мере перехода от эпохи κ≫κ_crit к текущему состоянию κ≈1.

Эта модель не требует введения новых частиц или полей и не нарушает общую теорию относительности. Она предлагает новый, геометрически самосогласованный взгляд на происхождение структур во Вселенной как результат естественного, неравновесного и саморегулирующегося перераспределения кривизны в системе брана–Bulk.

Если современная Вселенная – стабилизированная фаза этого процесса, то её наблюдаемая структура отражает не только историю вещества и излучения, но и историю гравитационной динамики: историю того, как изменялась связность, как формировались нелинейные ядра, как вращение стало универсальным свойством и как геометрические остатки прошлых фаз продолжают определять космическую эволюцию.

Предложенная схема объединяет эти явления в единое объяснение, в котором структура, вращение и тёмные компоненты предстают не как исключения, а как закономерные следствия ранней сверхгравитационной эпохи.

Благодарности

Автор выражает признательность коллегам за обсуждения и комментарии, позволившие уточнить аргументацию и углубить теоретическую часть работы.

Заявления

Работа не получила целевого финансирования. Автор заявляет об отсутствии конфликта интересов.