Моделирование динамики профессионального выбора с помощью концепции дифференциальных уравнений

Введение

Профессиональное самоопределение обучающихся является ключевой задачей современного образования, напрямую влияющей на личностную реализацию и экономическую эффективность общества. В условиях быстро меняющегося рынка труда, цифровой трансформации и роста неопределенности [5] формирование способности к осознанному профессиональному выбору становится критически важным. Классические педагогические и психологические теории [2, 3] заложили фундамент понимания данного процесса, описывая его стадии, факторы и механизмы. Современные исследования смещают фокус на рассмотрение самоопределения как нелинейного, контекстуального и непрерывного процесса построения карьеры.

Однако в практике образовательных учреждений сохраняется значительный методологический разрыв. Преобладающий инструментарий – психометрическое тестирование, анкетирование, разовые мероприятия – носит статический характер, фиксируя состояние обучающегося в конкретный момент, но не отражая внутреннюю динамику процесса: его колебания, противоречия, влияние случайных событий и нелинейность развития. Это приводит к ряду противоречий: между дискретностью измерений и непрерывностью процесса, между ориентацией на результат и игнорированием пути его достижения, между универсальными рекомендациями и необходимостью индивидуального подхода.

Возникает научная проблема, заключающаяся в отсутствии инструмента для описания и анализа профессионального самоопределения как процесса, развернутого во времени. Для ее решения предлагается применение концептуального аппарата теории динамических систем и дифференциальных уравнений [1, 4], что составляет новизну исследования. Цель работы – разработать и обосновать качественные динамические модели профессионального самоопределения, позволяющие классифицировать типы индивидуальных траекторий и обосновывать дифференцированные педагогические стратегии.

Объектом исследования выступает процесс профессионального самоопределения обучающихся как сложная, развивающаяся во времени система. Основным методом является математическое моделирование, а именно – качественный анализ простых дифференциальных уравнений.

Для формализации процесса вводится фазовая переменная , количественно отражающая степень склонности обучающегося к конкретному профессиональному выбору в диапазоне от –1 (абсолютное отвержение) до +1 (полная уверенность). Изменение данной переменной во времени описывается дифференциальным уравнением вида: , где функция отражает закон динамики, специфичный для определенного психологического типа.

Методология качественного анализа включает:

• содержательный анализ психолого-педагогических концепций для выделения базовых типов динамики;
• формализацию – подбор вида функции 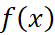для каждого типа;
• построение фазовых портретов – графического представления направлений изменений системы в каждой точке фазового пространства;
• выявление особых точек (аттракторов и отталкивателей), соответствующих устойчивым и неустойчивым состояниям системы;
• педагогическую интерпретацию полученных математических результатов, их перевод в стратегии сопровождения.

В результате проведенного анализа были выделены и формализованы три базовые динамические модели, каждая из которых описывает характерный тип процесса профессионального самоопределения.

1. Модель линейного роста («Искатель»)

Уравнением является , где – постоянная внешняя мотивация. Решение описывает равномерное движение. Поле направлений представляет собой однородный поток. Модель описывает обучающегося с выраженной внешней целеустремленностью, движущегося к выбору последовательно и с минимальным внутренним конфликтом. В качестве стратегии сопровождения подойдет структурированная информационная и ресурсная поддержка, помощь в построении пошагового плана.

2. Модель с отрицательной обратной связью («Конфликтный»)

Уравнением является , где – коэффициент внутреннего сопротивления. Решение показывает экспоненциальное затухание любого начального импульса. Единственный аттрактор – точка неопределенности (при ). Такая модель характерна для тревожных, склонных к рефлексии обучающихся, у которых любое формирующееся предпочтение порождает сомнения, возвращающие систему в состояние неопределенности. Следует избрать следующие стратегии сопровождения: снижение тревоги через нормализацию сомнений, техники принятия решений, организация профессиональных проб для получения конкретного опыта.

3. Модель логистического роста с самоусилением («Определяющийся»)

Уравнение для данной модели можно представить следующим образом: , где – коэффициент самоусиления. Решением является S-образная логистическая кривая. Фазовый портрет имеет два положения равновесия: неустойчивое (при ) и устойчивое (при – аттрактор). Такая модель является наиболее распространенной, отражающей этапы латентного накопления опыта, «кристаллизации» выбора и его последующего укрепления. Стратегия сопровождения включат создание обогащенной среды на начальном этапе, поддержку в момент кристаллизации выбора, ресурсное обеспечение на этапе углубления.

Предложенные модели демонстрируют, что традиционная профориентация, не учитывающая тип динамики, может быть неэффективна или даже вредна. Универсальная рекомендация для «Конфликтного» типа лишь усилит тревогу, в то время как для «Искателя» она будет полезна. Качественный анализ фазовых портретов, основанный на методах теории динамических систем [1, 4], позволяет педагогу диагностировать не только текущее состояние – x, но и характер динамики (знак и величина производной ), что открывает возможность для своевременного и адресного вмешательства в «точках бифуркации» – моментах, когда система наиболее чувствительна к управляющим воздействиям.

Заключение

Теоретический анализ подтвердил наличие методологического разрыва между динамической природой профессионального самоопределения и статическим инструментарием его диагностики в педагогической практике.

В качестве методологического решения предложен качественный подход на основе теории динамических систем, позволивший формализовать процесс через дифференциальные уравнения и фазовые портреты.

Выделены и математически описаны три базовые динамические модели («Искатель», «Конфликтный», «Определяющийся»), каждая из которых соответствует определенному психологическому типу и описывается специфическим дифференциальным уравнением.

Для каждой модели проведена педагогическая интерпретация и сформулированы дифференцированные стратегии профориентационного сопровождения, что составляет практическую ценность исследования.

Доказано, что переход от статической оценки к динамическому моделированию позволяет педагогу не только констатировать факт, но и понимать логику процесса, прогнозировать его развитие и выбирать оптимальные моменты и методы педагогического вмешательства.

Перспективы дальнейших исследований видятся в эмпирической верификации моделей на лонгитюдных данных, разработке на их основе диагностического инструментария для практикующих педагогов, а также в расширении моделей до многомерного случая для описания конкуренции нескольких профессиональных альтернатив.