Введение. В работе рассмотрены туннельные печи, предназначенные для обжига керамики, глазурованных изделий, декоративных кирпичей, черепицы и т.д. Кроме того данные печи могут быть использованы для термообработки и плавки легкоплавким металлов (рис. 1).
В качестве примера выберем печь типа ПТО-10.320/10. Рабочее пространство электропечи имеет форму проходного туннеля, образованного печными модулями [1]. В зависимости от требуемого графика нагрева и производительности печи количество обогреваемых и необогреваемых модулей может изменено. Гибкая модульная конструкция туннельной электропечи позволяет обеспечить требуемый технологический режим нагрева изделий при перемещении их по туннелю. Нагрев электропечи производится нагревателями спирального типа, расположенными на своде рабочей камеры обогреваемых модулей.

Рис. 1. Туннельная печь типа ПТО-10.320/10
Для повышения качества управление нагревом электропечи и движением печных тележек рассмотрим печь как объект с распределёнными параметрами для последующего синтеза распределённой системы управления.
Разработка математической модели. Математическую модель рассматриваемого объекта составим с использование дифференциальных уравнений в частных производных [2]. Ниже представлен фрагмент математической модели.
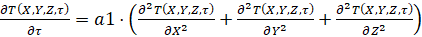 . (1)
. (1)
1) 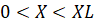 ,
, 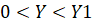 ,
, 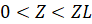 , 2)
, 2) 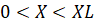 ,
, 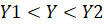 ,
, 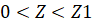 ,
,
3) 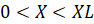 ,
, 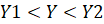 ,
, 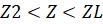 , 4)
, 4) 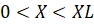 ,
, 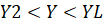 ,
, 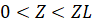 .
.
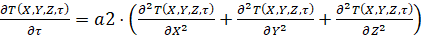 . (2)
. (2)
1) 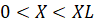 ,
, 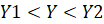 ,
, 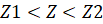 .
.
Граничные условия:
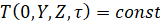 ,
, 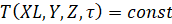 ,
,
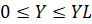 ,
, 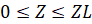 ,
, 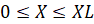 ,
, 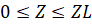 .
.
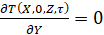 ,
, 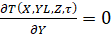 ,
, 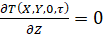 ,
, 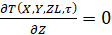 .
.
Из условия равенства тепловых потоков на границах раздела двух сред запишем следующие соотношения:
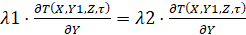 ,
, 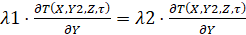 ,
,
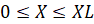 ,
,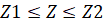 ,
, 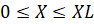 ,
, 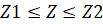 .
.
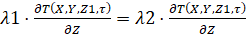 ,
, 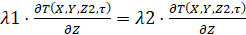 ,
,
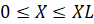 ,
, 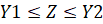 ,
, 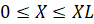 ,
, 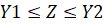 .
.
Для решения полученной системы уравнений воспользуемся явными схемами моделирования. Далее полученная система конечно-разностных уравнений решается на ЭВМ.
Анализ объекта управления. Анализ объекта управления будем производить с использованием теории систем с распределенными параметрами, т.к. данный объект является распределенным.
В соответствии с граничными условиями представим входное воздействие на объект в виде ряда Фурье по пространственным координатам. Уравнение, описывающее входное воздействие, будет иметь вид:
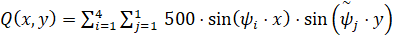 , (3)
, (3)
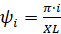 ,
, 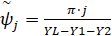 ,
,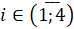 ,
,  ,
,
Графически, для разных значений параметра i, данное входное воздействие можно представить в виде:
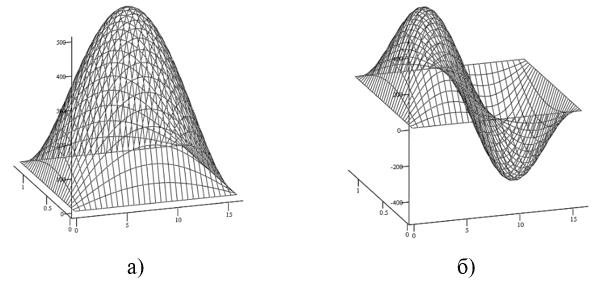
Рис. 2. Входное воздействие 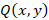 a) при
a) при  , б) при
, б) при 
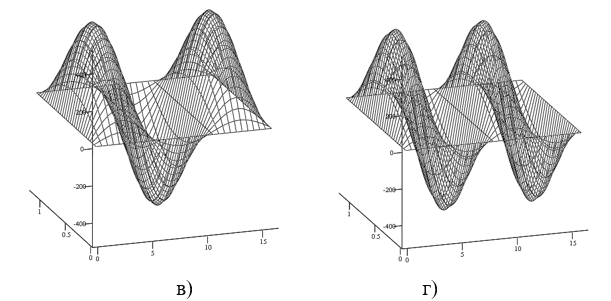
Рис. 3. Входное воздействие 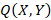 в) при
в) при 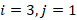 , г)
, г) 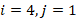
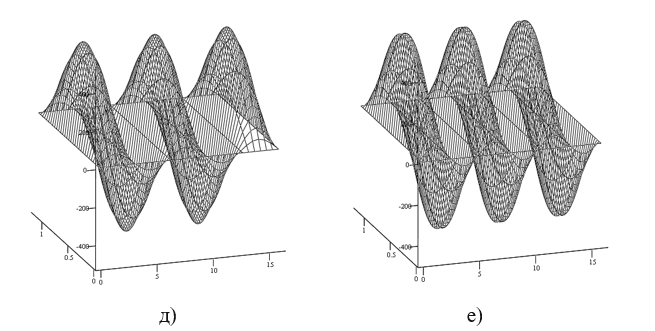
Рис. 4. Входное воздействие 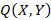 д) при
д) при 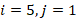 , е) при
, е) при 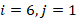
Подавая поочередно каждое из входных воздействий, представленных на рисунках 2-4, построим графики переходных процессов в фиксированных точках расположения датчиков. Далее, полученные функции распределенных входных воздействий и выходных сигналов используем для определения частотных характеристик.
Частотные характеристики туннельной печи. Для построения частотных характеристик аппроксимируем передаточные функции объекта, по каждой моде входного воздействия как апериодическое звено с чистым запаздыванием [3].
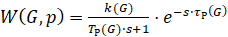 , (4)
, (4)
С использованием полученных передаточных функций объекта построим частотные характеристики разомкнутой системы. Для этого произведем замену оператора Лапласа s на комплексную частоту jω. Заменяя, получим
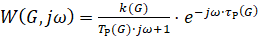 . (5)
. (5)
Изменяя переменную ω в пределе от 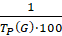 до
до 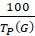 , для каждого значения обобщенной координаты G, построим частотные характеристики распределенного объекта [4].
, для каждого значения обобщенной координаты G, построим частотные характеристики распределенного объекта [4].
Распределенный годограф объекта управления представлен на рис. 5.
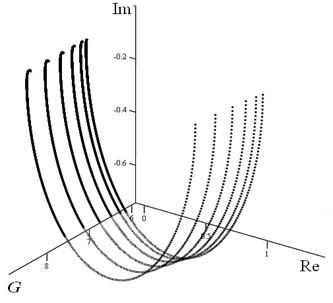
Рис. 5. Распределенный годограф собственных значений
Также были получены логарифмические амплитудная и фазовая частотные характеристики.
Заключение. В работе исследованы характеристики туннельной печи типа ПТО-10.320/10. Рассмотрен процесс построения математической модели исследуемого объекта управления с использование дифференциальных уравнений в частных производных и её решение численными методами, с целью проведения экспериментов.
Полученная математическая модель позволила построить частотные характеристики, с помощью которых были проведены исследования с целью последующего синтеза системы управления температурным полем печи.

.png&w=640&q=75)