Развитие и диагностика уровня умения формировать умозаключения в курсе физики основной школы

Введение

В соответствии с Концепцией модернизации содержания предмета «физика» главной целью курса основной школы является формирование и развитие естественнонаучной грамотности учащихся, что предполагает компетентное поведение ученика в процессе решения естественнонаучных задач. Считается, что необходимым фундаментом этого, является в том числе сформированность познавательных универсальных учебных действий, часть которых определена в Примерной основной образовательной программе основного общего образования [1] как умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение и делать выводы.

Недостаточный уровень развития логического мышления делает процесс обучения неэффективным, приводит к обеднению содержания обучения и существенному разбросу оценок школьников при контроле усвоения учебного материала. Качество и успешность обучения школьников зависят от уровня развития их познавательных умений, неразрывно связанных как с объемом усвоенных знаний, так и с уровнем сформированности логического мышления. Однако, если измерение объема усвоенных знаний является привычным педагогическим действием сравнения с эталоном (знает – не знает), то измерение умения формировать умозаключения представляет собой серьезную проблему из-за отсутствия предметных методик. Оценивание преподавателем достигнутого уровня развития мыслительных операций чаще всего происходит интуитивно на основе имеющегося личного опыта. При этом результат оценивания, выраженный, как правило, в относительных баллах, не позволяет описать динамику его изменения.

Для оценивания с этих позиций эффективности учебного процесса необходима разработка дисциплинарных диагностических методик. Они должны позволить сравнивать между собой результаты измерений, проведенных в разное время, в различных группах и на различном стимульном материале.

Целью исследования является разработка методики развития и измерения, достигнутого учениками основной школы уровня умения формировать умозаключения. В курсе физики наиболее подходящей базой для разработки диагностирующих методик является практикум по решению задач. Уровень умения формировать умозаключения может быть измерен по качеству действий, используемых учащимся при решении учебных физических задач. Тестовые задачи выступают в качестве диагностирующего воздействия, реакция на которое содержит информацию об уровне совершаемых в процессе решения основных мыслительных операций. Основная проблема заключается в определении типа задач, которые могут быть использованы с одной стороны, в качестве учебных для развития умения формировать умозаключения, и с другой стороны, в качестве тестовых для измерения достигнутого уровня.

Умозаключение – это форма мышления, посредством которой из одного или нескольких суждений выводится новое. Любое умозаключение состоит из посылок, заключения и процедуры вывода. Посылками умозаключения называют исходные суждения, из которых выводится новое суждение. Заключением называется новое суждение, полученное логическим путем из посылок. Логический переход от посылок к заключению называется выводом. Отношение логического следования между посылками и заключением предполагает связь между посылками по содержанию.

Частный вид умозаключений – силлогизмы. Они отличаются тем, что и в посылках, и в заключении присутствуют высказывания, которые на основании наличия или отсутствия каких-то свойств у объектов позволяют сделать вывод о наличии или отсутствии у них других свойств. Наиболее простым и часто встречающимся вариантом является простой категорический силлогизм. Он состоит из двух посылок. В первой посылке говорится об отношении терминов А и В, во второй – об отношениях терминов В и С. На основании этого делается вывод об отношении терминов А и С. Такой вывод возможен потому, что обе посылки содержат общий термин В, который опосредует содержательную связь между терминами А и С.

В физическом задачном практикуме обычно присутствуют силлогизмы, в которых, в скрытом виде содержится вся необходимая для формирования умозаключения информация. Последовательность решения следующая: после анализа исходных данных и формирования промежуточных заключений задача может быть сведена к простому силлогизму. Рассмотрим это на примере задачи, взятой из демонстрационного варианта ОГЭ по физике:

Задача 1

Шар 1 последовательно взвешивают на рычажных весах с шаром 2 и шаром 3 (рис. 1). Для объемов шаров справедливо соотношение V1=V2<V3. Какой шар имеет минимальную плотность?

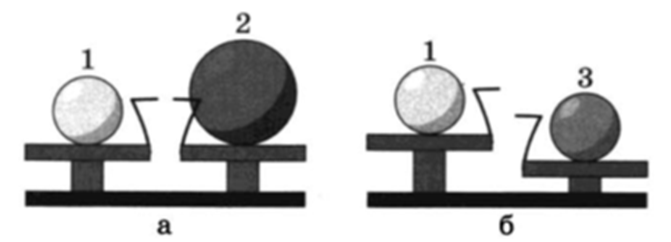
Рис. 1

Решение

После анализа образной информации, содержащейся в рисунках а и б, делаем промежуточные заключения:

1. Если m1=m2, a V1<V2, то ;
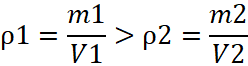2. Если m1<m3, a V1=V3, то .

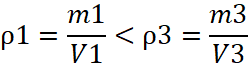Заключения 1 и 2 являются исходными посылками простого силлогизма с общим термином : если , и , то . Вывод: минимальную плотность имеет второй шар.

Рассмотренная задача может быть задана в вербальной форме:

Задача 2

Даны три шара с массами m1=m2<m3 и объемами V2>V1=V3. Какой шар имеет минимальную плотность?

Для развития умения формировать умозаключения рассмотренный пример силлогистической задачи может быть усложнен введением количественных соотношений между терминами:

Задача 3

Шары 1, 2 и 3 последовательно взвешивают на весах. Оказалось, что массы первого и второго шаров равны m1=m2, а масса третьего шара в 2 раза больше массы первого m3=2∙m1. Первый и третий шары имеют равные объемы V1=V3, а объем второго в 2 раза больше объема первого V2=2∙V1. Во сколько раз наибольшая плотность одного из шаров превышает наименьшую?

Решение

Последовательность решения остается прежней. После анализа исходной информации, формируем промежуточные заключения:

1. Если m1=m2, а V2=2∙V1, то ;
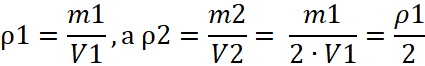2. Если m3=2∙m1, a V1=V3, то .

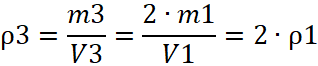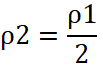Заключения 1 и 2 являются исходными посылками простого силлогизма с общим термином если , и то наибольшая плотность третьего шара превышает наименьшую плотность второго шара в 4 раза.

Решение таких задач представляет собой сложные сочетания операций анализа, сравнения и основано на построении умозаключений в решении силлогизмов. Необходимые мыслительные операции – анализ, сравнение и логические умозаключения на их основе. Подобные силлогизмы допускают усложнение за счет введения дополнительных терминов.

Материалы и методы исследования

Измерение уровня умения формировать умозаключения при решении физических задач рассмотрим на примере теста, основанного на установлении количественных отношений при решении силлогизмов, содержащих общие и частные посылки. Их выполнение представляет собой сложное сочетание операций анализа, сравнения и основано на логическом мышлении в решении силлогизмов. В качестве стимульного материала в тестовом задании использованы понятия из раздела «кинематика» курса физики основной школы. Для их успешного выполнения необходимо предварительное усвоение приведенных в тестах терминов и соотношений. Однако, для акцентирования внимания и действий учащихся на формировании умозаключений, тест содержит всю необходимую знаниевую составляющую часть (в тесте приведены аналитические соотношения, необходимые для получения решения). Необходимые операции – анализ, сравнение и логические умозаключения на их основе. Время выполнения теста – около 30 мин. Перед началом тестирования проводится инструктаж: «На бланке задания приведены 20 задач, решения которых оцениваются в 0 баллов (неправильный ответ) или 1 балл (правильный ответ)».

Пример тестового задания (приведен один блок из пяти). С вершин трех наклонных плоскостей с углами наклона α₁>α₂>α₃ одновременно начинают скользить без трения три тела. Через t секунд тела на наклонной плоскости имеют скорости v₁, v₂, v₃ и соответственно перемещения s₁, s₂, s₃. При этом скорости изменяются пропорционально времени v=at, а перемещения пропорционально квадрату времени s = at²/2. Если в конце второй секунды:

1. s₁ больше s₂ в 4 раза, а s₂ больше s₃ в 2 раза, то во сколько раз a₁ больше a₃?
2. s₁ больше s₂ в 4 раза, а s₂ больше s₃ в 2 раза, то во сколько раз v₁ больше v₃?
3. a₁ больше a₃ в 4 раза, а a₁ больше a₂ в 2 раза, то во сколько раз s₂ больше s₃?
4. v₂ больше v₃ в 2 раза, а v₁ больше v₃ в 8 раз, то во сколько раз s₁ больше s₃?

По рассмотренным примерам тестовых задач были проведены контрольные измерения в группах школьников 9-х классов.

Результаты измерений и их обсуждение

Результаты тестирования были статистически обработаны в последовательности, описанной в работах [2; 3, с. 175-180]. Была сформирована бинарная матрица тестовых результатов, содержащая ответы студентов (1- верный ответ, 0 – неверный). Затем была определена мера сложности каждой i-ой задачи g_i, как отношение числа правильно ответивших на i-ый вопрос, к полному числу участников тестирования. Также были определены оценки каждого j-го участника b_j на отрезке [0, 1], как относительная доля правильно решенных им задач, средняя оценка b_СР всей группы тестируемых, и другие параметры распределения результатов измерений: дисперсия D, среднеквадратичное отклонение σ, медиана, асимметрия и эксцесс. Эти параметры описывают особенности функции распределения плотности вероятности правильного ответа по оценочной шкале b. Асимметрия распределения положительна, если основная часть индивидуальных оценок b лежит справа от среднего значения. При больших положительных значениях параметра асимметрии тестовое задание является простым и излишне легким. Асимметрия отрицательна, если большая часть индивидуальных баллов лежит слева от среднего значения. При больших отрицательных значениях тест является излишне трудным для выполнения. В хорошо сбалансированном по трудности тесте распределение баллов имеет вид нормального распределения Гаусса.

Распределение плотности вероятности решения рассмотренного тестового задания на отрезке [0, 1] приближенно может быть описано функцией Гаусса с наиболее вероятным значением оценки b_mod=0,58 и среднеквадратичным отклонением σ=0,1 (рис. 2).

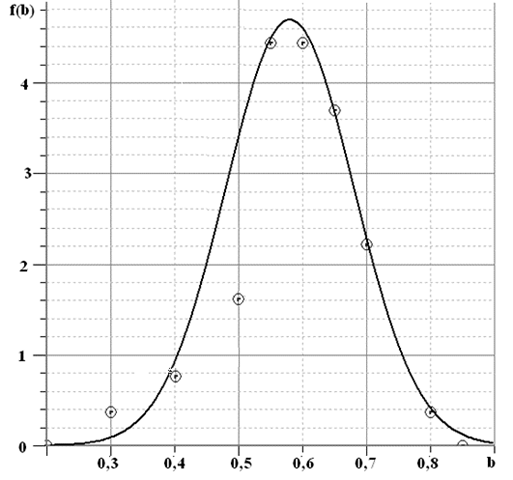
Рис. 2. Распределение плотности вероятности f(b) по шкале оценок b

Числовые параметры распределения следующие:

• размах Db=b_max – b_min =0,5;
• математическое ожидание b_СР =0,58;
• дисперсия D=0,011;
• среднеквадратичное отклонение σ=0,10.

Классический вариант обработки результатов тестирования позволяет провести дифференциацию школьников по оценкам тестирования. Однако, эти оценки, выраженные измеряемой индикаторной переменной b, зависят от сложности тестовых заданий и не являются однозначными характеристиками уровня установления количественных отношений. Вместе с тем они позволяют достаточно точно провести дифференциацию учащихся класса по уровню измеряемого качества.

Для дифференциации тестируемых по результатам тестовых испытаний весь диапазон изменения оценок b обычно разбивают на три участка:

1. Первый соответствует низкому уровню измеряемого качества с неудовлетворительными оценками и диапазоном изменения первичной оценки .
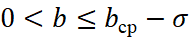2. Второй участок оценочной шкалы представляет собой диапазон средних оценок измеряемого качества и соответствует изменению первичных оценок b в пределах от 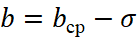до .
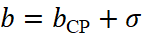3. Третий участок первичных баллов 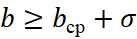соответствует превосходному уровню тестируемого качества.

По результатам выполнения теста количество учащихся 9 класса, получивших оценки из интервала (0<b<0,48), оказалось около 20% от их общего числа. Для этой группы характерен низкий уровень умения формировать умозаключения. Второй участок оценочной шкалы, определенный как или 0,48<b<0,68, соответствует диапазону средних оценок и нормального уровня развития операций анализа и сравнения в решении силлогизмов. Такие результаты были получены в 68% всех испытаний. Третий участок отличных оценок или b>0,68 соответствует превосходному уровню умения формировать умозаключения и совершения операций анализа и сравнения на учебном стимульном материале. Таких результатов было 11% от общего количества испытаний.

Заключение

1. Качество и успешность обучения физике школьников зависят от уровня развития одного из познавательных универсальных учебных действий – умения формировать умозаключения. Для его развития и измерения достигнутого уровня, а также наблюдения динамики его изменения в курсе физики основной школы возможно использование учебных задач, имеющих структуру классического силлогизма, усложненного введением дополнительных количественных соотношений и сформулированных как в образной, так и в вербальной формах.
2. Тестирование с использованием комплекта тестовых задач этого типа и классического варианта статистической обработки результатов позволяет провести дифференциацию учащихся по достигнутому уровню развития умения формировать умозаключения.