Оптимизация многослойного армирования земляных сооружений: алгоритм на основе теории игр

Применение геосинтетических материалов для армирования земляных насыпей, дамб и откосов стало стандартом в современном строительстве. Однако выбор параметров армирования остаётся сложной задачей из-за противоречивых требований: повышение прочности и устойчивости требует увеличения числа слоёв и их прочности, тогда как снижение стоимости и трудоёмкости монтажа требует минимизации количества материалов. Традиционные методы не формализуют компромисс между этими целями и часто опираются на субъективные допущения. В связи с этим актуальной становится задача разработки формализованного алгоритма, который бы однозначно определял оптимальное решение.

Цель настоящего исследования – разработать алгоритм оптимизации параметров армирования на основе теории игр, позволяющий находить баланс между противоречивыми критериями (устойчивость, стоимость, осадка) через поиск равновесия по Нэшу. Новизна подхода заключается в переносе математического аппарата теории игр в область геотехнического проектирования, где равновесие Нэша выступает инструментом формализации компромисса между «игроками» – условными участниками процесса, представляющими интересы прочности и экономики. Практическая значимость состоит в повышении надёжности проектных решений за счёт объективного выбора параметров армирования без субъективных весовых коэффициентов.

Рассмотрим насыпь высотой H с многослойным армированием геосинтетиком. Требуется определить количество слоёв n, высоты их расположения h_i (i=1,…,n), прочность геосинтетика в каждом слое T_i, а также величину нахлёста полотен l. Критериями оптимизации выступают: коэффициент устойчивости откоса F_s → max, осадка насыпи S → min (с ограничением S ≤ S_доп), стоимость конструкции С → min.

Для формализации задачи представим процесс выбора параметров как некооперативную игру двух условных игроков: «Прочность» (максимизирует F_s и минимизирует S) и «Экономика» (минимизирует С). Стратегиями игроков выступают наборы параметров (n, h_i, T_i, l). Равновесие Нэша определяется как сценарий s*, в котором ни один игрок не может улучшить свой выигрыш, изменив стратегию в одиночку 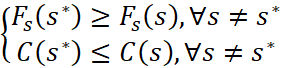[1]:

, (1)

Алгоритм поиска равновесия состоит из следующих шагов. На первом этапе генерируется множество допустимых сценариев S={s₁, s₂,…,s_m}, где каждый сценарий s_j – это вектор параметров (n_j, h_1j,…, h_nj, T_nj, l_j). Параметры варьируются в диапазонах , , , с учётом ограничений: минимальное расстояние между слоями , максимальная прочность геосинтетика . Генерация сценариев выполняется методом полного перебора или методом Монте‑Карло в зависимости от размерности задачи.

На втором этапе для каждого сценария s_j вычисляются значения целевых функций. Коэффициент устойчивости F_sj определяется методом круглоцилиндрических поверхностей скольжения по ВСН 04-71 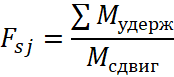[2]:

, (2)

Осадка S_j рассчитывается послойным суммированием по СП 22.13330.2016 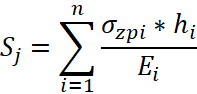[3]:

, (3)

Где – вертикальное напряжение в слое, – толщина слоя, – модуль деформации.

Стоимость складывается из затрат на материалы и работы:

, (4)

Где – общая длина геотекстиля, – площадь насыпи.

Третий этап – нормализация критериев к безразмерным индексам [0,1] для построения платёжных матриц [1]. Для критериев, которые нужно максимизировать (например, ), применяется формула:

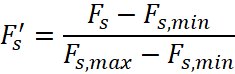, (5)

Для критериев, которые нужно минимизировать (например, C, S), используется:

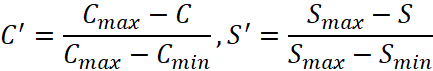, (6)

Платёжная матрица для игрока «Прочность» формируется как , для игрока «Экономика» – как .

На четвёртом этапе осуществляется поиск равновесия Нэша. Для малого числа сценариев применяется аналитический перебор всех комбинаций с проверкой условий равновесия. Для больших задач используется линейное программирование [5]:

Максимизировать v при условиях:

, (7)

, (8)

Альтернативно применяется итерационный алгоритм, основанный на последовательном улучшении стратегий игроков до сходимости. Результатом является равновесный сценарий s*=(n*, h_i*, T_i*, l*).

Пятый этап – верификация результата. Проверяются условия [2], [3], а также соответствие стоимости С* бюджетным ограничениям (допуск 5–10%). Верификация выполняется сравнением с расчётами по СП 45.13330 [4], численным моделированием в программных комплексах и анализом чувствительности к вариациям параметров грунта ().

Алгоритм на основе теории игр превосходит традиционные методы проектирования, поскольку через равновесие Нэша объективно балансирует противоречивые критерии (устойчивость, стоимость, осадка) без субъективных весовых коэффициентов. Его ключевые достоинства – прозрачность, воспроизводимость, гибкость (возможность учёта дополнительных критериев и ограничений) и однозначность решения. Однако метод требует значительных вычислительных ресурсов при росте числа параметров, чувствителен к точности моделей грунта и нагрузок, а также предполагает глубокую подготовку данных и знание теории игр. Несмотря на эти ограничения, алгоритм открывает новый подход к геосинтетическому армированию: он устраняет субъективность, обеспечивает оптимальный баланс прочности, деформативности и стоимости и позволяет снижать затраты при сохранении устойчивости насыпи. Алгоритм перспективен для ответственных геотехнических проектов, где критичны точность и обоснованность решений. Дальнейшее развитие может включать интеграцию с численными методами (МКЭ) и учёт стохастичности свойств грунта для повышения робастности результатов.