Основополагающим показателем для обеспечения высокой боевой готовности в теории надежности является понятие «надежности», которое понимается как свойство техники, способной выполнять заданные функции, при определенных условиях эксплуатации сохранять свои основные характеристики согласно установленных пределах качества как совокупности свойств техники, которые обусловливают ее способность удовлетворять определенным потребностям [1]. Одной из составляющих обеспечения готовности пожарной техники является надежность, т.к. более общим нежели понятие «надежность» является понятие «качества» [2].
Исходя из вышеобозначенного, качественный показатель пожарной техники включает следующие требования: оперативной подвижности; высокой боевой готовности; эффективной подачи огнетушащих средств; эргономики; технической эстетки.
В ходе восстановления поломки пожарной техники важное место занимают вопросы диагностирования. Классификация диагностических параметров должна соответствовать ГОСТ 25044-81 [3].
При использовании в качестве диагностических параметров постепенно изменяющиеся величины, то для их описания можно использовать целевую функцию. Данная целевая функция выражает соответствующее изменение структурных параметров объекта диагностирования. Закономерность изменения диагностического параметра может быть выражена следующим уравнением [4]:
S=Sн+vlα, (1)
где Sн – начальное значение диагностирующего параметра; v – интенсивность изменения диагностирующего параметра; lα – показатель степени, определяющий характер изменения параметра.
Используя данное уравнение можно определить ресурс объекта диагностирования, т.е. пробег, при котором диагностический параметр достигнет предельной величины.
С целью проведения комплексной оценки технического состояния пожарной техники предлагается ввести совокупный показатель безотказности данных средств – Pб, основанный на оценках вероятностей безотказной работы основных составных частей/агрегатов рассматриваемой техники.
Если диагностические параметры рассматриваемой системы выходят за границы предельных значений, в этом случае вероятность ее адекватной и безотказной работы будет принимать нулевое значение:
D≥Dпред→P=1-F=1-1=0, (2)
где D, Dпред – фактическое и предельное значения диагностических параметров рассматриваемой система пожарной техники; P – вероятность безотказной работы системы; F– вероятность отказов.
Модель вероятностных состояний включает оценку состояний основных частей/агрегатов пожарной единицы. Взаимосвязью со структурными параметрами Y определяется выбор диагностических параметров S. При помощи логических соотношений при отказах элементов записываются условия работоспособности системы.
На рисунке представлен граф выхода из строя и восстановления исследуемой системы пожарной техники.
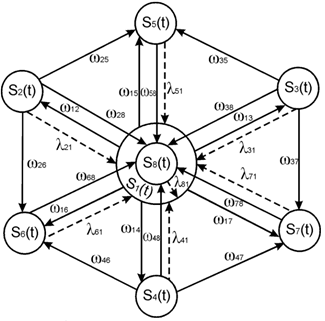
Рис. Граф выхода из строя и восстановления исследуемой системы пожарной техники: S1(t) – состояние исправности; S2(t) - S8(t) – состояние исправности агрегатов пожарной единицы; λij – параметр, отражающий интенсивность восстановления; ωij – параметр, отражающий поток отказов
На рисунке в виде кружка изображено каждое из состояний, а стрелками обозначены возможные переходы из одного состояния в другое.
Возможность получения расчетных формул определяется видом логической модели. Наибольшее распространения получил Марковский анализ с целью описания надежности и е параметров.
Совокупность рассматриваемых узлов исследуемой системы можно представить как физическую систему S, где протекают случайные процессы с дискретными состояниями: Si, число которых примем конечным и их интервал (1; n). При этом под системой S будем понимать технологическое устройство – пожарная техника. Процесс называется дискретным, если система S скачками время от времени переходит из одного состояния Siв Sj.
Далее предлагается метод дифференциальных уравнений, для случайного процесса с дискретными состояниями и непрерывным временем. В этом случае рассмотрим пожарную единицу техники, как систему S, у которой переход из состояния Si в состояние Sj происходит в произвольный момент времени t. Автомобиль может находиться в одном из восьми возможных состояний (рисунок). Каждому из состояний соответствует определенное событие – параметрический отказ одной из систем, влияющих на безопасность и безотказность движения или возможное их совместное появление (параметрический отказ всех трех систем).
Надежность автомобиля в состояниях S2 - S4 определяется вероятностью безотказной работы конкретной отказавшей системы, а в состояниях S5 - S8 – согласно теореме умножения вероятностей произведением вероятностей безотказной работы систем, у которых наблюдается параметрический отказ.
Необходимо найти вероятности состояний такого процесса, т.е.
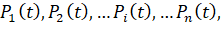 (3)
(3)
где 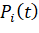 – вероятность, что система будет находиться в состоянии Si в любой момент времени t.
– вероятность, что система будет находиться в состоянии Si в любой момент времени t.
Следует отметить, что для любого момента времени система вероятностей состояний равна 1, по причине того, что события, которые состоят в том, что система находится в состояниях S1… Snнесовместимы в любой момент времени t и образуют полную группу событий и по этой причине система дифференциальных уравнений должна быть дополнена следующими нормированными условиями:
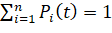 , (4)
, (4)
где n – число возможных состояний; 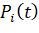 – вероятность нахождения системы в i -м состоянии.
– вероятность нахождения системы в i -м состоянии.
Если известны интенсивности перехода (параметр потока отказов) ωij и интенсивности восстановления λij для всех пар состояний Si, Sj,то возможно определить вероятности состояний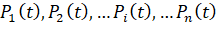 , как функцию времени. Придадим t малое приращение Δt для нахождения вероятности того, что система будет находиться в состоянии S1 в момент времени t+Δt.
, как функцию времени. Придадим t малое приращение Δt для нахождения вероятности того, что система будет находиться в состоянии S1 в момент времени t+Δt.
Данное событие может произойти восьмью способами: в момент t система уже была в состоянии S1, а за время Δt не вышла из этого состояния; в момент t система была в состоянии S2-S8, а за время Δt перешла из него в S1.
В виде произведения вероятности P1(t) того, что система была в состоянии S1, на условную вероятность того, что, если бы система была в состоянии S1, она за время Δt не перешла бы из него в состояние Sn+1, определим вероятность для первого варианта. Эта условная вероятность равна 1-ωij Δt.
Аналогично, вероятность последующих вариантов равна Pn+1(t)ωij Δt.
Применяя правило сложения вероятностей, получим следующее равенство:
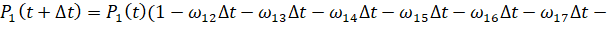
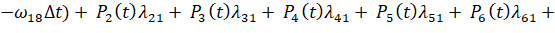
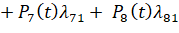 . (5)
. (5)
Раскроем скобки в правой части равенства, далее 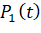 перенесем в левую и разделим обе части равенства на Δt, и перейдем к пределу при ∆t→0:
перенесем в левую и разделим обе части равенства на Δt, и перейдем к пределу при ∆t→0:
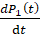 =
=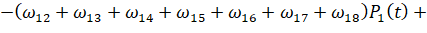
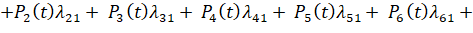
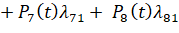 , (6)
, (6)
где 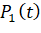 – вероятность нахождения системы – пожарная техника в состоянии S1 (исправное состояние); ωij – параметр потока отказов; λij – интенсивность восстановления.
– вероятность нахождения системы – пожарная техника в состоянии S1 (исправное состояние); ωij – параметр потока отказов; λij – интенсивность восстановления.
Таким образом, получено дифференциальное уравнение, которому должна удовлетворять функция 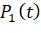 . Аналогичным образом получим уравнения и для остальных вероятностных состояний
. Аналогичным образом получим уравнения и для остальных вероятностных состояний 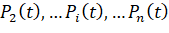 .
.
Представленный граф состояний дает возможность составить систему дифференциальных уравнений Колмогорова [5].
Решение данной системы дает возможность определить искомые вероятности:
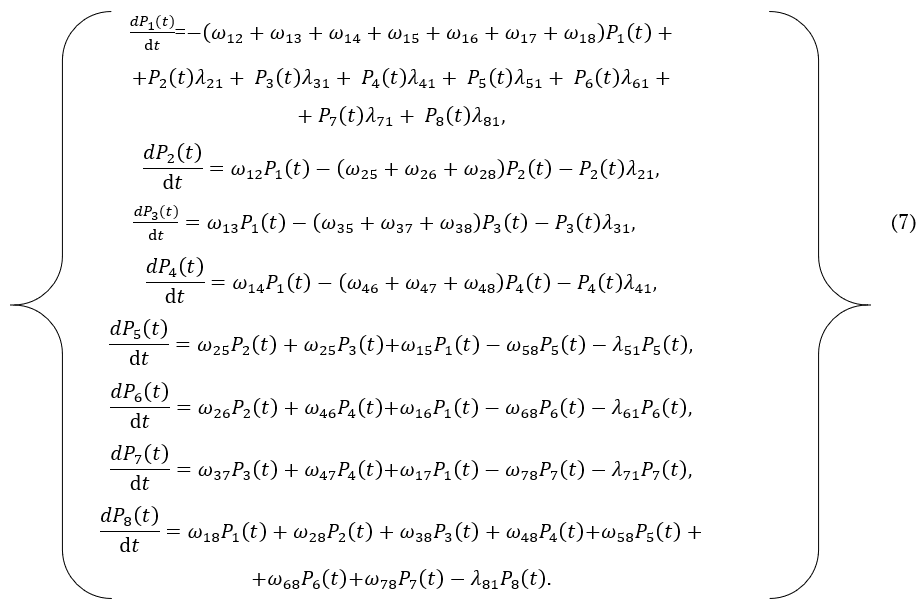
В расчетах показателей надежности для достаточно длительных интервалов времени без большой погрешности вероятности состояний системы можно определять по установившимся средним (предельным) вероятностям. Вероятности установившихся состояний (при ∆t→∞) находятся решением обычной системы линейных алгебраических уравнений, полученных из системы дифференциальных уравнений приравниванием производных нулю, совместно с нормировочным условием (3).
Таким образом в результате преобразований, получим вероятность нахождения системы в состоянии S1 – пожарная единица техники исправна:
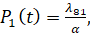 (8)
(8)
где α – переменная, зависимая от параметров потока отказов ωij и интенсивности восстановления λij.
Представим вероятности нахождения системы в состояниях S2 – S8:
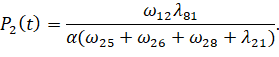 (9)
(9)
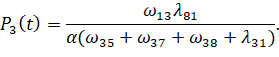 (10)
(10)
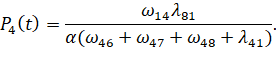 (11)
(11)
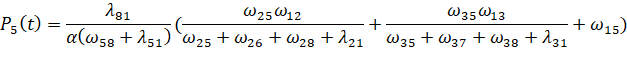 (12)
(12)
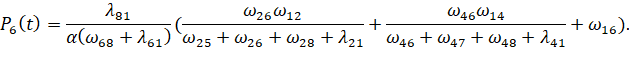 (13)
(13)
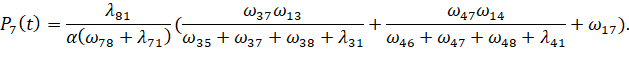 (14)
(14)
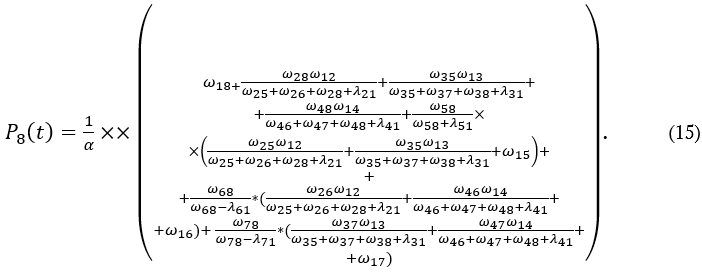
Система оценки выхода из строя и восстановления исследуемой системы пожарной техники автомобиля, отказ которой характерен для конкретного состояния, является лимитирующей в определении комплексного показателя безотказности автотранспортного средства.
Например, для состояния формула комплексного показателя безотказности примет следующий вид:
Pобщ=PМР*PГР*PРУ, (16)
где PМР – вероятности безотказной работы механической части системы; PГР – вероятности безотказной работы гидравлической части системы; PЭМР – вероятности безотказной работы электромеханической части системы.
С целью сокращения затрат по обнаружению неисправности необходимо: снизить стоимость обнаружения конкретной причины (или комплекса причин) за счет предварительного поэлементного диагностирования; рационально сформировать само множество проверяемых факторов.
Следовательно, формируются предпосылки для разработки алгоритма последовательности проведения проверок и устранения отдельных управляемых факторов.

.png&w=640&q=75)