При создании многих устройств, подверженных температурным воздействиям, необходимо проводить исследования на предмет их надежности и учитывающий их поведение в рабочем цикле. В статье предлагается пошаговый алгоритм исследования, где рассматривается построение схемы и ход анализа температурного поля полого объекта цилиндрической формы средствами математического моделирования. При помощи такой модели становится возможным описание процесса нагрева любых объектов цилиндрической формы, таких как: трубы различного рода, технологические емкости, части опорных конструкций, сопло реактивного двигателя или парового/газового инжектора, и т.д., в условиях их контакта с окружающей средой.
В структуре моделировании процессов теплообмена будут фигурировать три области распределения тепла, которые характеризуются различными коэффициентами температуропроводности и различными пространственными координатами, в виде радиуса и угла поворота [1, с. 14]. Рассматриваемый объект (в разрезе) изображен на рисунке 1.
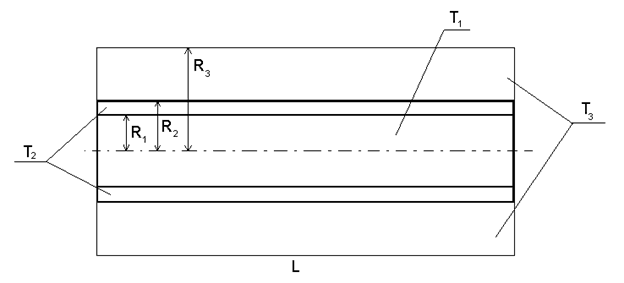
Рис. Рассматриваемый полый объект цилиндрической формы
Ниже представлена математическая модель представленного объекта [1, с. 17; 4, с. 23], включающая в себя все три вышеупомянутые области:
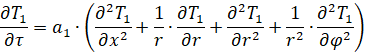 (1)
(1)
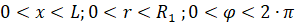
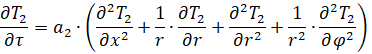 (2)
(2)
при 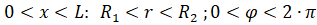
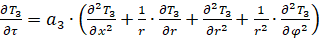 (3)
(3)
при 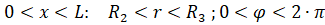
где T1 (x,r,t), T2 (x,r,t) , T3 (x,r,t) – температурное поле в пространстве внутри объекта, в теле объекта, и во внешней среде; a1, a2, a3 – коэффициенты температуропроводности воздушной среды внутри объекта, тела объекта и внешней воздушной среды соответственно, L – максимальная высота объекта, r – радиус объекта, x – высота объекта, R1 – радиус среды внутри объекта, R2 – радиус среды объекта и тела объекта, R3 – радиус всей системы: среды внутри объекта, тела объекта и окружающей среды.
Далее, согласно порядка исследования, необходимо определить граничные условия математической модели. Это, в первую очередь, будут условия неизолированности системы. В приводимом здесь примере исследования условно примем, что окружающая среда – воздух. Известно, что воздух обладает крайне малой температуропроводностью, следовательно - достаточно взять небольшой участок воздушной среды, который отобразит отток тепла от тела объекта, далее становится возможным применение граничных условий:
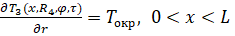 (4)
(4)
где Токр – температура окружающей среды.
Также необходимо определить условие равенства тепловых потоков на границе сред:
– граница между средой внутри объекта и самим объектом:
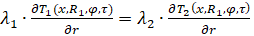 (5)
(5)
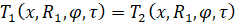 ;
;
– границы между телом объекта и окружающей средой:
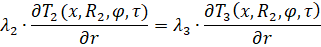 (6)
(6)
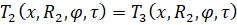 ;
;
где λ1 – коэффициент теплопроводности среды внутри объекта, λ2 – коэффициент теплопроводности самого тела, λ3 – коэффициент теплопроводности окружающей среды.
Теперь необходимо ввести определение условий оттока тепла с границ рассматриваемого пространства при x = 0 и x = L:
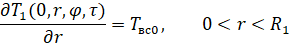
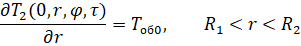
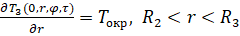 (7)
(7)
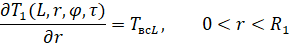
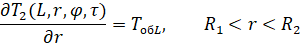
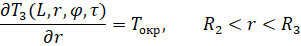
где Твс0 и ТвсL – температура внутренней среды объекта при x = 0 и x = L соответственно; Tоб0 и ТобL – температура тела объекта при x = 0 и x = L соответственно.
На следующем этапе необходимо ввести начальные условия переходного процесса в каждой из трех сред:
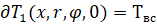
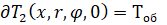 (8)
(8)
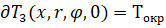
Для дальнейшего анализа необходимо привести уравнение к дискретному виду при помощи метода сеток [5, с. 145].
Подробный анализ процесса распределения тепла в представленной модели предоставит нам исчерпывающую информацию:
a) о топологии распределения тепловых полей по телу объекта,
b) о теплообмене объекта с внешней и внутренней средой.
Предложенный порядок анализа процесса распределения тепла в представленной здесь модели, в конечном итоге, дает математически обоснованный базис для построения модели регулятора управления температурным полем [2, с. 43; 3, с. 54], что является уже следующим этапом в создании автоматической системы контроля и управления состоянием сложных теплонагруженных объектов и темой следующей статьи.

.png&w=640&q=75)